Национальный исследовательский Томский политехнический университет «Прикладная химическая термодинамика» Смороков Андрей Аркадьевич wolfraum@yandex.ru vk.com/wolfraum1993 1
Опрос 2
Приведите соотношение Эйлера для температуры, давления и объема. Из первого закона термодинамики выведите уравнение работы идеального газа в изотермическом процессе. Приведите постулат о температуре (нулевой закон термодинамики). Опираясь на термодинамические явления, предположите, почему производители запрещают нагревать дистиллированную воду в микроволновых печах. 3
Методы оценки изобарной теплоемкости Корреляционные соотношения. Метод требует наличия большого массива данных, на основе которых проводится расчет неизвестной величины. Инкрементные (аддитивные схемы. Любое свойство есть сумма вкладов свойств компонентов. Для расчета термодинамических свойств неорганических соединений с использованием корреляционных соотношений рекомендуется использовать: А.Г. Морачевский, И.Б. Сладков «Термодинамические расчеты в металлургии» и т.п. Для инкрементных схем рекомендуется использовать базу данных ТКВ, а также справочная литература. 4
Корреляционные схемы Основываясь на массиве данных по веществам, сходных по природе и структуре возможно построение зависимостей (обычно линейной), исходя из которых возможно вычисление недостающих величин. Основной проблемой данного метода является недостаток данных по свойствам многих соединений. Для оценки возможности построения линейной зависимости проводят определение коэффициента корреляции r. Последний показывает насколько хорошовыбранные точки удовлетворяют уравнению прямой линии: y=a*x+b. Коэффициент корреляции изменяется в пределах от -1 до +1. при r=-1 или 1, выбранные точки ложатся на прямую, а при r=0 линейная связь между x и y полностью отсутствует. 5
Расчет коэффициента корреляции Пусть х и у – свойства, откладываемые по оси абсцисс и ординат соответственно. Для определения коэффициента корреляции для совокупности иксов и игреков определяют их средние арифметические ( и ), далее находят коэффициент корреляции. 6
Расчет коэффициента корреляции Критическое значение выбирают исходя из доверительной и числа степеней свободы ( f=n-2 ). На практике чаще всего используют доверительную вероятность 95%. Если окажется, что коэффициент корреляции меньше критического, и что какая-то точка сильно удалена от прямой, то эту точку исключают из рассмотрения и вычисления повторяют. После установления пригодности исходных данных для построения линейной зависимости проводят определение коэффициентов линейной зависимости ( а и b ): 7
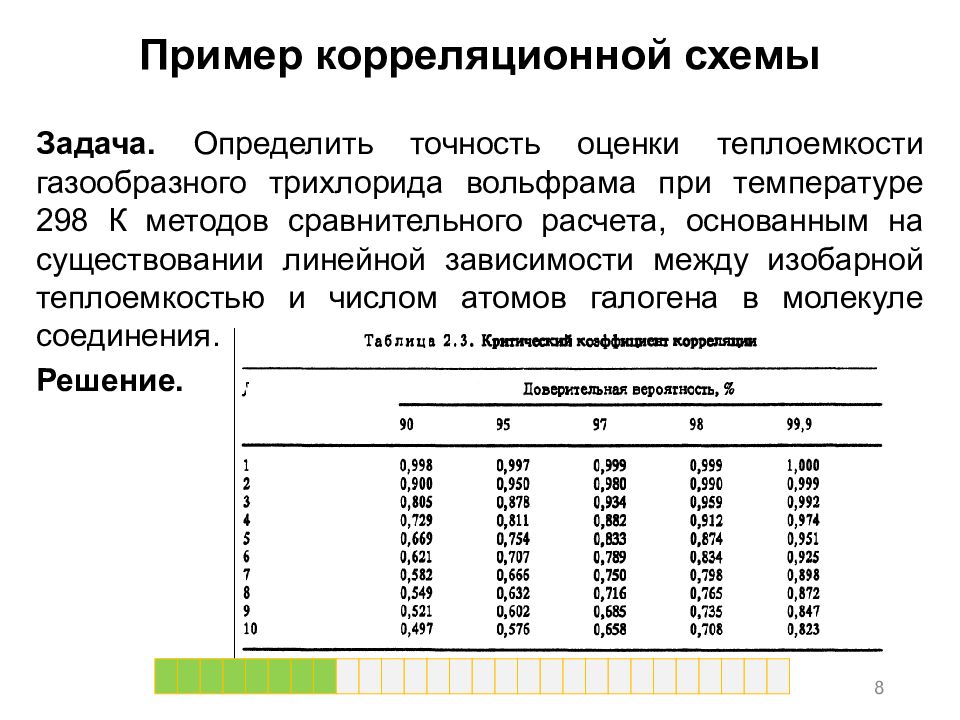
Пример корреляционной схемы Задача. Определить точность оценки теплоемкости газообразного трихлорида вольфрама при температуре 298 К методов сравнительного расчета, основанным на существовании линейной зависимости между изобарной теплоемкостью и числом атомов галогена в молекуле соединения. Решение. 8
Пример корреляционной схемы 9
Пример корреляционной схемы 10
Пример корреляционной схемы 11
Пример корреляционной схемы 12
Пример корреляционной схемы 13 В результате, с доверительной вероятностью 95 % погрешность найденного значения теплоемкости не должна превышать плюс-минус 9,4*100/79 = 11,4 %. Основываясь на экспериментальном значении (80 Дж/(моль*К)) получаем погрешность 1,38 %. Таким образом, получаемое значение не выходит за пределы допустимого значения.
Инкрементные схемы Данные схемы базируются на постулате об аддитивности свойств. С р ( CaAl 2 O 4 ) = С* р ( CaO ) + С* р ( Al 2 O 3 ) Значения инкрементов С* р ( CaO ) и С* р ( Al 2 O 3 ) отличаются от значений С р ( CaO ) и С р ( Al 2 O 3 ) при этой температуре, но С* р ( CaO ) не равно С р ( CaO ). Если принять, что они равны, то получаем правило Неймана-Коппа. Минус – изначально завязано на том, что изменение теплоемкости реакции равно нулю. Работает на небольшом температурном интервале. Наиболее распространен. Относительно хорошо работают на оксидах, солях, галогенидов. Плохо - для сплавов. 14
Примеры оценки теплоемкости Метод Кубашевского. С р = a+bT-c*(T^(-2)). Основная цель состоит в попытке расчетного определения коэффициентовв уравнении температурного ряда теплоемкости в уравнении Майера и Келли. За опорные точки принимаются температуры 298 К и температура плавления (фазового перехода). При этом делаются следующие допущения: А) теплоемкость в точке плавления равняется С р, пл. = 30,3* m Б) третий параметр в формуле с=419000* m. При известной С р, 298К можно к следующим формулам для нахождения коэффициентов: с=419000* m. b = (25.64*m + 419000*m*(T пл. ^(-2) - С р, 298 ) / ( T пл. - 298) a = С р, 298 – 298*b+4.71*m T пл - температура плавления, m – число атомов в соединении. 15
Примеры оценки теплоемкости Метод Ивановой. С р = m * (22.14+8.32/T прев. ). T прев - температура первого фазового перехода (обычно плавление), m – число атомов в соединении. Применим для определения изобарной теплоемкости простых неорганических соединений, кроме боридов, карбидов и нитридов. Другие способы приблизительного расчета термодинамических функций, в т.ч. изобарной теплоемкости приведены в «Термодинамические расчеты в металлургии» А.Г.Морачевский, И.Б.Сладков 16
Термохимия Термохимия – наука о тепловых эффектах химических процессов. Тепловой эффект химической реакции – это мера изменения запаса энергии в результате протекания данного процесса; он определяется суммой выделенной (поглощенной) при реакции теплоты и совершенной внешней работы (выраженной в тех же тепловых единицах), когда реагируют между собой молярные количества вещества. Основным законом является закон Гесса. 17
Закон Гесса Теплота химической реакции при постоянном объеме и давлении не зависит от промежуточных стадий, через которые проходил процесс, а определяется только начальным и конечным состоянием продуктов и реагентов при условии, что единственной работой совершаемой системой является работа расширения. Если реакция протекает в растворе или в твердой фазе, где изменение объема незначительно, то Δ H = Δ U + p Δ V ≈ Δ U. Если же в реакции участвуют идеальные газы, то при постоянной температуре Δ H = Δ U + p Δ V = Δ U + Δ nRT где Δ n – изменение числа моль газообразных веществ, принимающих участие в реакции. 18
Стандартное и отсчетное состояния Стандартное состояние привязано к давлению 1 бар. P o = 1 бар Температура в термодинамике не стандартизируется. Есть отсчетная температура (0 или 298 К). Могут обозначать как T ref. Стандартные состояния: конденсированная фаза и газовая фаза. Для конденсированного состояния выбирают наиболее устойчивое состояние при давлении 1 бар и любой температуры. За стандартное состояние реального газа выбирают гипотетическое состояние, когда газ при заданной температуре и давлению 1 бар газ ведет себя как идеальный газ. 19
Стандартные тепловые эффекты Стандартная энтальпия реакции. Δ r Н о. Это тепловой эффект химической реакции при постоянном давлении, когда все участники процесса находятся в стандартном состоянии 2. Стандартная энтальпия образования. Δ f Н о. Это тепловой эффект образования 1 моль вещества из простых веществ в стандартном состоянии 3. Стандартная энтальпия сгорания. Δ c Н о. Это тепловой эффект реакции окисления 1 моль вещества кислородом (фтором) при давлении 1 бар. 20
Стандартные тепловые эффекты CaO + Al 2 O 3 → CaAl 2 O 4 Ca + 2 Al + 2 O 2 → CaAl 2 O 4 2 Al + 1.5 O 2 → Al 2 O 3 Al + 0.75 O 2 → 0.5 Al 2 O 3 21
Стандартные тепловые эффекты CaO + Al 2 O 3 → CaAl 2 O 4 Δ r Н о Ca + 2 Al + 2 O 2 → CaAl 2 O 4 Δ f Н о 2 Al + 1.5 O 2 → Al 2 O 3 Δ f Н о Al + 0.75 O 2 → 0.5 Al 2 O 3 Δ c Н о 22
Следствия закона Гесса 1. Стандартная энтальпия образования. Стандартная энтальпия реакции равна алгебраической сумме стандартных энтальпий участников реакции Σν i A i = 0. Из продуктов вычитают реагенты. 2. Стандартная энтальпия сгорания. Стандартная энтальпия реакции при постоянной температуре равна взятой с обратным знаком алгебраическая сумма стандартных энтальпий сгорания. Из свойств реагентов вычитаем свойства продуктов. 23
Пример следствий из закона Гесса Сграфит → Салмаз. При горении графита и алмаза получается оксид углерода (IV) и выделяются соответствующие количества теплоты: Сграфит + O 2 = С O 2, ΔН 1 = –393,51 кДж; Салмаз + O 2 = С O 2, ΔН 2 = –395,34 кДж. Следовательно, вычитая из первого уравнения второе получаем Сграфит → Салмаз, Δ Н 3 = Δ Н 1 – Δ Н 2 = 1,83 кДж. Таким образом, переход графита в алмаз сопровождается поглощением сравнительно небольшого количества теплоты, т.е. является несамопроизвольным. 24
Уравнение Кирхгофа. Зависимость теплового эффекта реакции от температуры Дифференцируя по температуре (при постоянном давлении) равенство ΔН = Н 2 − Н 1, получаем выражение вида ∂(Δ Н)/∂ T= (∂ Н 2 /∂ T) р – (∂ Н 1 /∂ T) р где ΔН – тепловой эффект химической реакции, а индексы 1 и 2 относятся, к продуктам реакции и исходным веществам. Здесь полезным может быть напоминание определения такой характеристики вещества, как теплоемкость. Теплоемкость – количество теплоты, которое надо подать системе, чтобы увеличить ее температуру на один градус. Так как производная (∂Н/∂T) р является теплоемкостью системы при постоянном давлении, то выражение можно переписать ∂(ΔН)/∂T = С р2 – С р1 = ΔС р 25
Уравнение Кирхгофа. Зависимость теплового эффекта реакции от температуры Здесь ΔС р – изменение изобарной теплоемкости системы в химической реакции при постоянной температуре. Для реакции, представленной в общем виде, aA + bВ = cC + dD величина ΔС р будет равна: ΔС р = (c·C р (C) + d·C р (D)) − (a·C р (A) + b·C р (B)), здесь a, b, c и d – стехиометрические коэффициенты в уравнении реакции с участием веществ A, B, C и D. 26
Экспериментальные методы определения тепловых эффектов 1. Калориметры сгорания (калориметрическая бомба). Сосуд постоянного объема. Измеряет изменение внутренней энергии. H = U + pV Δ r H = Δ r U + Δ r ( pV ) Если конденсированная фаза, то Δ r ( pV ) приблизительно равна 0 и Δ r H = Δ r U. Если газ, причем идеальный, то: Δ r ( pV ) = p 1 V 1 - p 2 V 2 = n 1 RT - n 2 RT = Δ r νRT Δ r ν – количество изменения числа молей газообразных веществ. https://www.youtube.com/watch?v=0JMf2ZRwTRw 27
Экспериментальные методы определения тепловых эффектов 2. Калориметры растворения. Растворяют в: воде, соляной кислоте – невысокие температуры Высокие температуры – свинцово-боратный расплав и натрий-вольфраматный расплав (температура около 1000 К). Общая проблема этих методов – идентификация продуктов сгорания и растворения. 3. Прямая реакционная калориметрия. Проблема заключается в интерпретации результатов и их воспроизводимости. 28
