Первый слайд презентации: Структурная кристаллография
Элементы структурной кристаллографии
Слайд 2
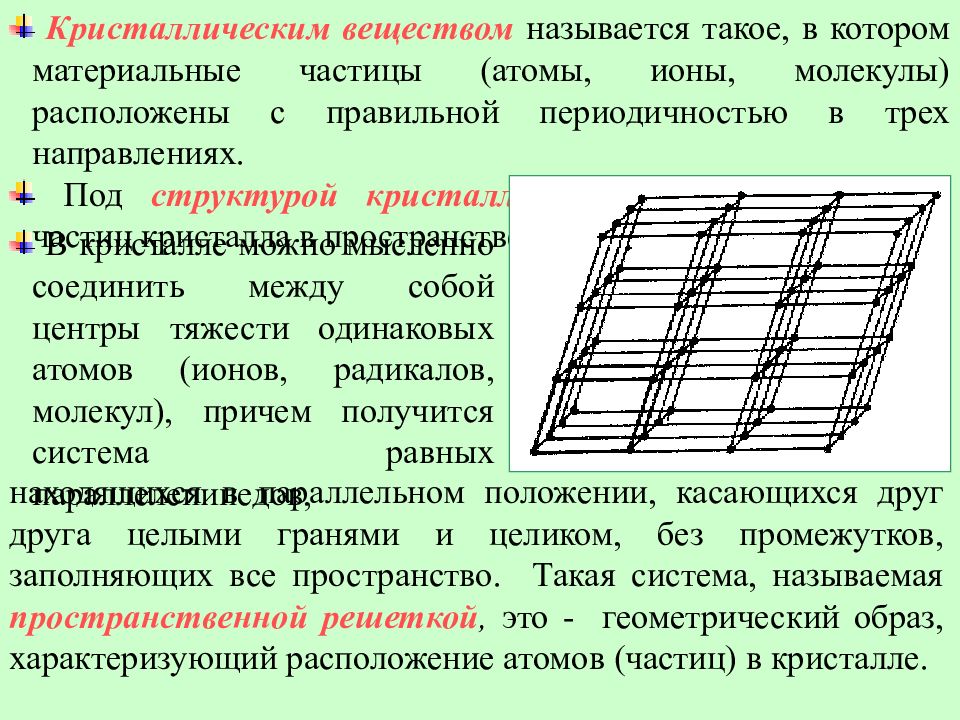
Кристаллическим веществом называется такое, в котором материальные частицы (атомы, ионы, молекулы) расположены с правильной периодичностью в трех направлениях. Под структурой кристалла понимают расположение частиц кристалла в пространстве. В кристалле можно мысленно соединить между собой центры тяжести одинаковых атомов (ионов, радикалов, молекул), причем получится система равных параллелепипедов, находящихся в параллельном положении, касающихся друг друга целыми гранями и целиком, без промежутков, заполняющих все пространство. Такая система, называемая пространственной решеткой, это - геометрический образ, характеризующий расположение атомов (частиц) в кристалле.
Слайд 3
Наименьший параллелепипед, с помощью которого можно построить всю пространственную решетку непрерывными параллельными переносами в трех направлениях, называется элементарной ячейкой. Три основных вектора, являющихся ребрами элементарной ячейки, называют трансляциями или осевыми единицами. Абсолютную величину трансляций а, b, с называют периодами решетки. Периоды решетки и три угла между ребрами ячейки α, β, γ (осевые углы) однозначно характеризуют элементарную ячейку. Трансляции можно выбирать разными способами. Принято выбирать их так, чтобы периоды имели наименьшее значение, а форма элементарной ячейки была возможно ближе к прямоугольному параллелепипеду при условии, что элементарная ячейка сохранит симметрию, свойственную кристаллу в целом.
Слайд 4
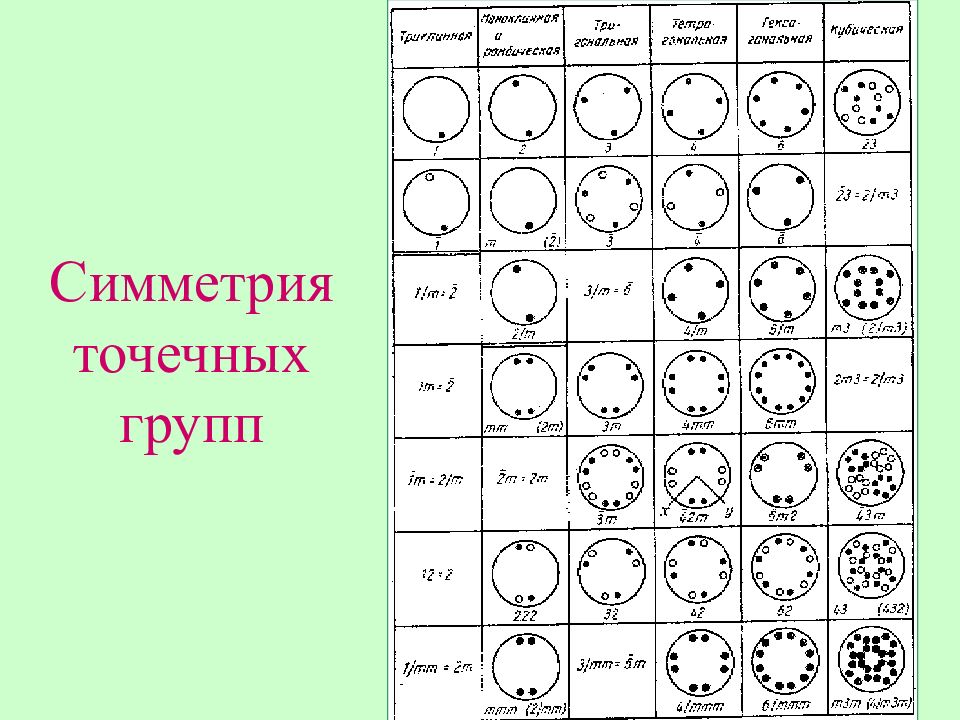
Все многообразие пространственных решеток разделяют на семь систем — сингоний, исходя из соотношения между осевыми единицами и углами. В основу классификации было положено наличие тех или иных элементов симметрии в кристалле. Структуры, имеющие одни и те же определяющие элементы симметрии, принадлежат одной и той же сингоний. Однако реальный набор элементов симметрии структуры, кроме определяющих, может включать и дополнительные элементы симметрии. Число независимых сочетаний элементов симметрии решетки ( пространственных групп ) составляет 230. По наличию сходных элементов симметрии 230 пространственных групп можно объединить в 32 точечных группы ( классы симметрии ).
Слайд 6
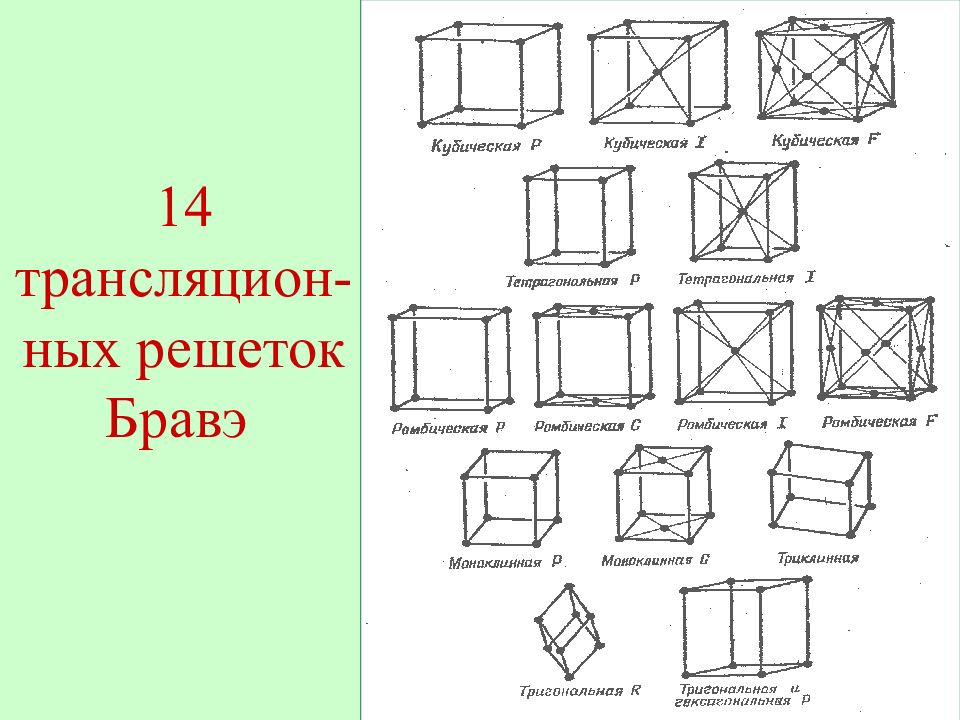
Если все частицы кристалла, принадлежащие одной элементарной ячейке, заменить их центрами тяжести, то окажется, что в пространстве их можно периодически распространить (транслировать) четырнадцатью разными способами. Условия, с помощью которых из бесконечного возможного числа параллелепипедов можно выбрать определенный, характеризующий решетку в целом, сформулированы Бравэ: сингония выбранного параллелепипеда должна быть такой же, как и сингония всей решетки; число прямых углов между ребрами параллелепипеда должно быть максимальным; число равных осевых отрезков должно быть также максимальным; при соблюдении первых трех условий объем его должен быть минимальным. Таким образом, существуют 14 трансляционных решеток Бравэ.
Т рансляционная решетка и ее элементарный параллелепипед должны обладать симметрией, свойственной кристаллу в целом. К азалось бы, сложную кубическую гранецентрированную решетку F, можно было заменить примитивной ромбоэдрической решеткой R, но тогда элементарный параллелепипед ее не будет обладать симметрией, свойственной кубу, что противо - речит правилам выбора трансля - ционной ячейки. Нарушение принципа соответствия симметрии кристалла симметрии ячейки Бравэ
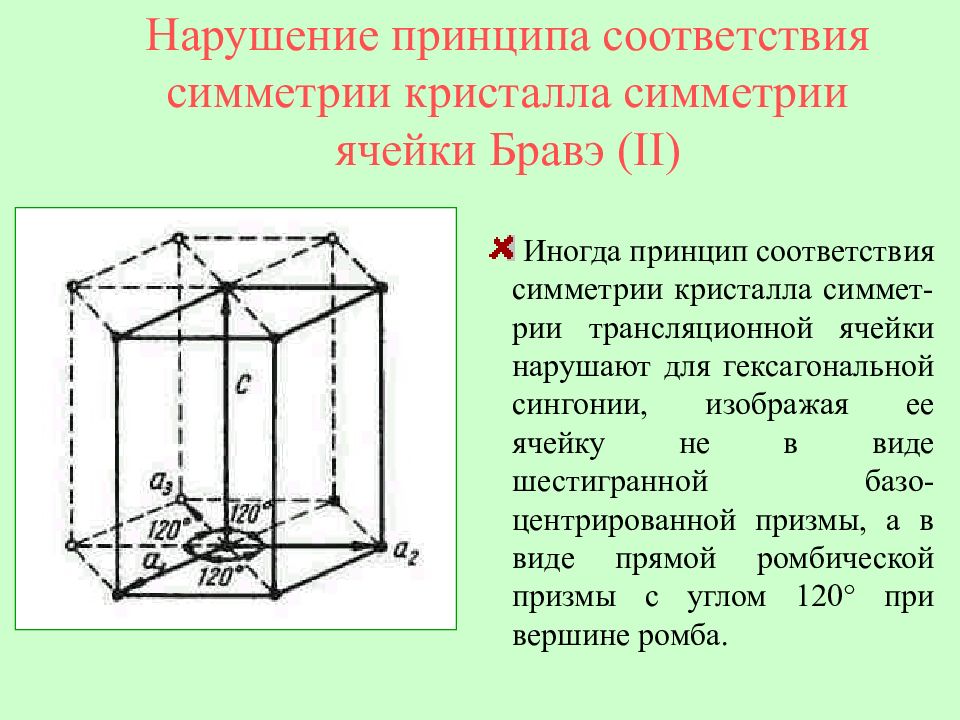
Иногда принцип соответствия симметрии кристалла симмет - рии трансляционной ячейки нарушают для гексагональной сингонии, изображая ее ячейку не в виде шестигранной базо - центрированной призмы, а в виде прямой ромбической призмы с углом 120° при вершине ромба. Нарушение принципа соответствия симметрии кристалла симметрии ячейки Бравэ (II)
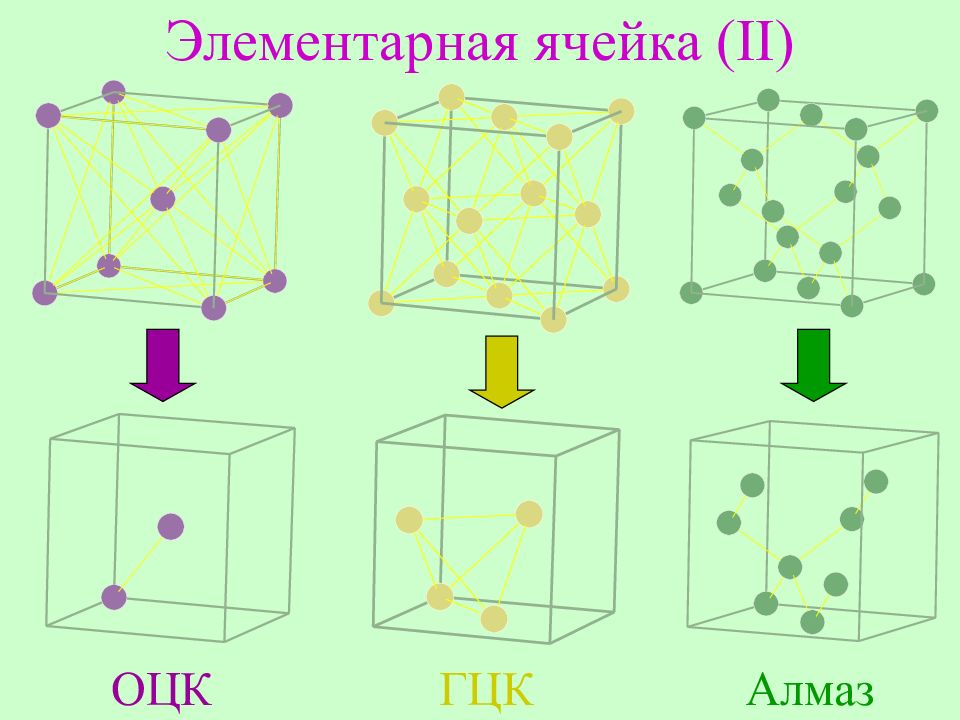
Слайд 10: Элементарная ячейка ( I)
Атом, расположенный внутри ячейки, приходится целиком на долю данной ячейки. Атом, расположенный на грани ячейки, входит одновременно в две ячейки и, следовательно, на долю ячейки приходится одной второй своей частью. Атом, расположенный на ребре, приходится на долю одной ячейки одной четвертой частью. Атом, расположенный в вершине, принадлежит одновременно восьми соседним ячейкам, т.е. на одну ячейку приходится одна восьмая часть.
Слайд 12
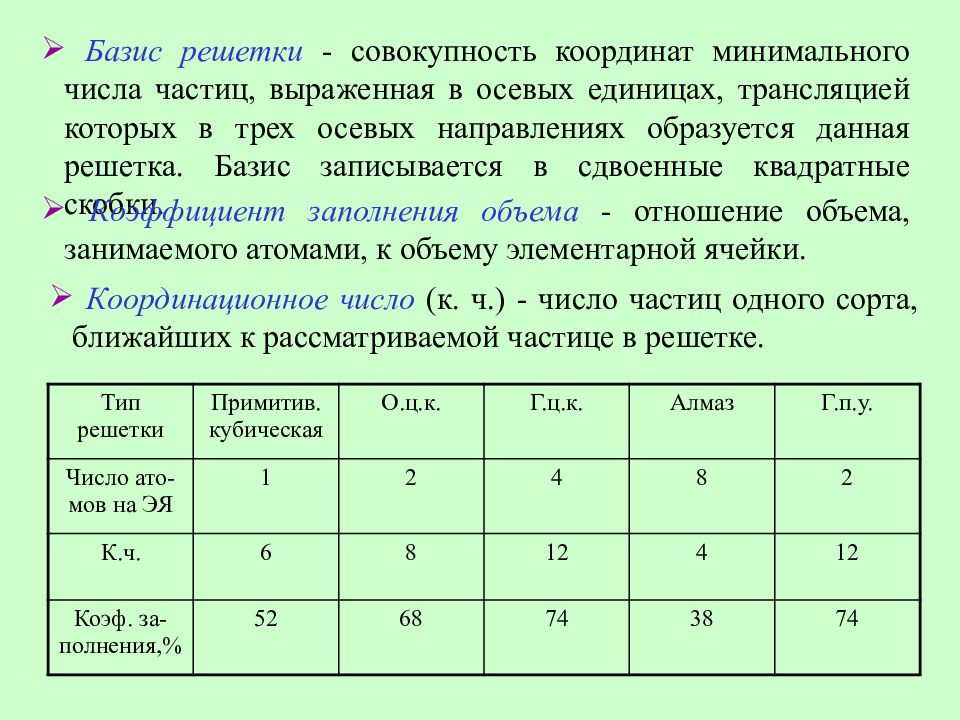
Базис решетки - совокупность координат минимального числа частиц, выраженная в осевых единицах, трансляцией которых в трех осевых направлениях образуется данная решетка. Базис записывается в сдвоенные квадратные скобки. К оординационно е числ о ( к. ч. ) - числ о частиц одного сорта, ближайших к рассматриваемой частице в решетке. К оэффициент заполнения объема - отношени е объема, занимаемого атомами, к объему элементарной ячейки. Тип решетки Примитив. кубическая О.ц.к. Г.ц.к. Алмаз Г.п.у. Число ато-мов на ЭЯ 1 2 4 8 2 К.ч. 6 8 12 4 12 Коэф. за-полнения,% 52 68 74 38 74
Слайд 13: Индексы плоскостей
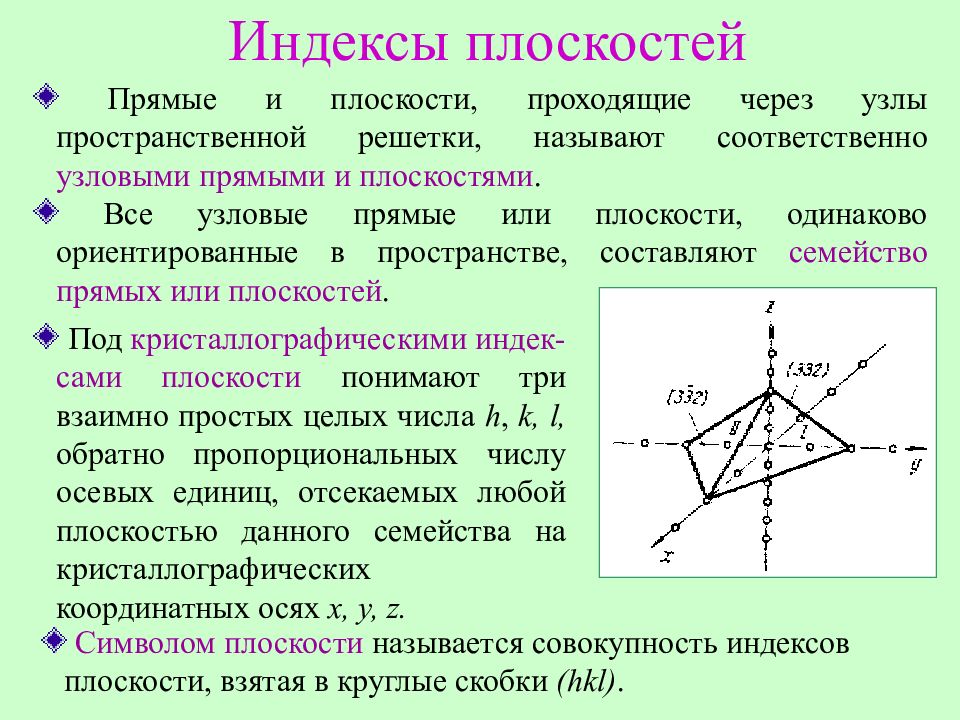
Прямые и плоскости, проходящие через узлы пространственной решетки, называют соответственно узловыми прямыми и плоскостями. Все узловые прямые или плоскости, одинаково ориентированные в пространстве, составляют семейство прямых или плоскостей. Под кристаллографическими индек - сами плоскости понимают три взаимно простых целых числа h, k, l, обратно пропорциональных числу осевых единиц, отсекаемых любой плоскостью данного семейства на кристаллографических координатных осях х, у, z. Символом плоскости называется совокупность индексов плоскости, взятая в круглые скобки ( hkl ).
Слайд 14: Индексы направлений
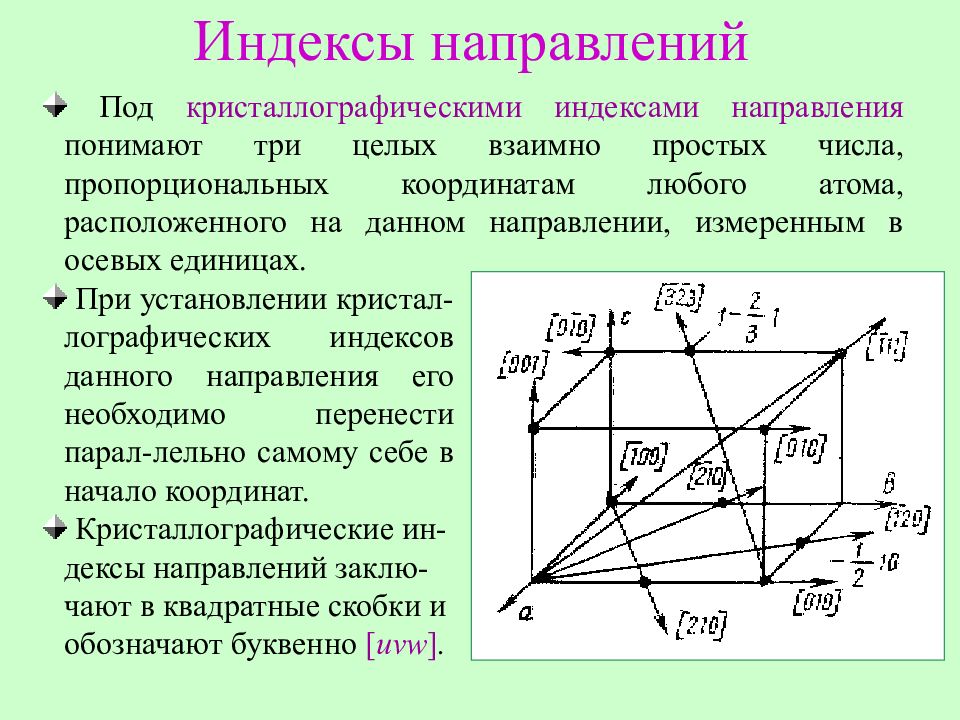
Под кристаллографическими индексами направления понимают три целых взаимно простых числа, пропорциональных координатам любого атома, расположенного на данном направлении, измеренным в осевых единицах. При установлении кристал - лографических индексов данного направления его необходимо перенести парал - лельно самому себе в начало координат. Кристаллографические ин - дексы направлений заклю - чают в квадратные скобки и обозначают буквенно [ u v w ].
Слайд 15: Некоторые соотношения
Индексы направления [ uvw ], по которому пересекаются две плоскости, связаны с индексами этих плоскостей ( h 1 k 1 l 1 ) и ( h 2 k 2 l 2 ) следующей системой уравнений: Аналогично индексы плоскости ( hkl ), в которой лежат два направления [ u 1 v 1 w 1 ] и [ u 2 v 2 w 2 ], определяются из симметричной системы: Угол между двумя направлениями в кубической сингонии с индексами [ u 1 v 1 w 1 ] и [ u 2 v 2 w 2 ], и может быть найден из уравнения
Слайд 16: Симметрия кристалла
Симметри я является общим свойством кристаллического тела, а анализ ее — одним из главнейших методов кристал - лографии. Анизотропия строения кристалла проявляется в анизотропии свойств. При этом, согласно основному положению кристаллофизики — принципу Неймана, симметрия любого физического свойства кристалла не может быть выше симметрии строения кристалла. Р асположение материальных частиц в пространстве может быть охарактеризовано с помощью так называемых элементов симметрии. Элемент симметрии — геометрический образ, воздействие которого на периодически повторяющуюся систему точек приводит к совмещению этой системы точек со своим первоначальным положением в пространстве.
Слайд 17: Закрытые элементы симметрии ( I)
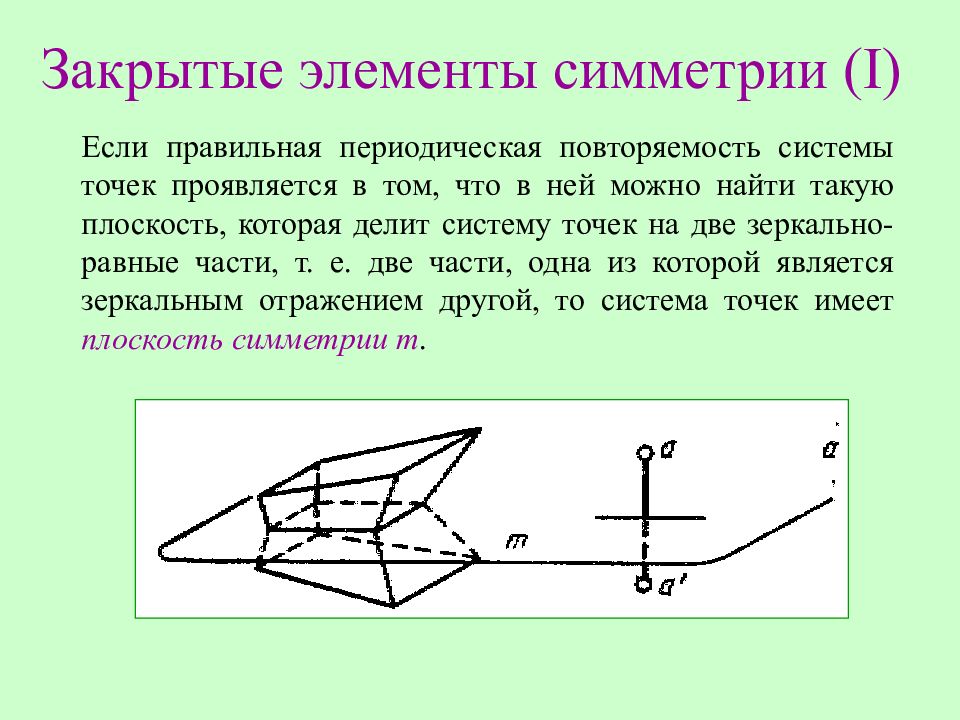
Если правильная периодическая повторяемость системы точек проявляется в том, что в ней можно найти такую плоскость, которая делит систему точек на две зеркально-равные части, т. е. две части, одна из которой является зеркальным отражением другой, то система точек имеет плоскость симметрии m.
Слайд 18: Закрытые элементы симметрии ( II)
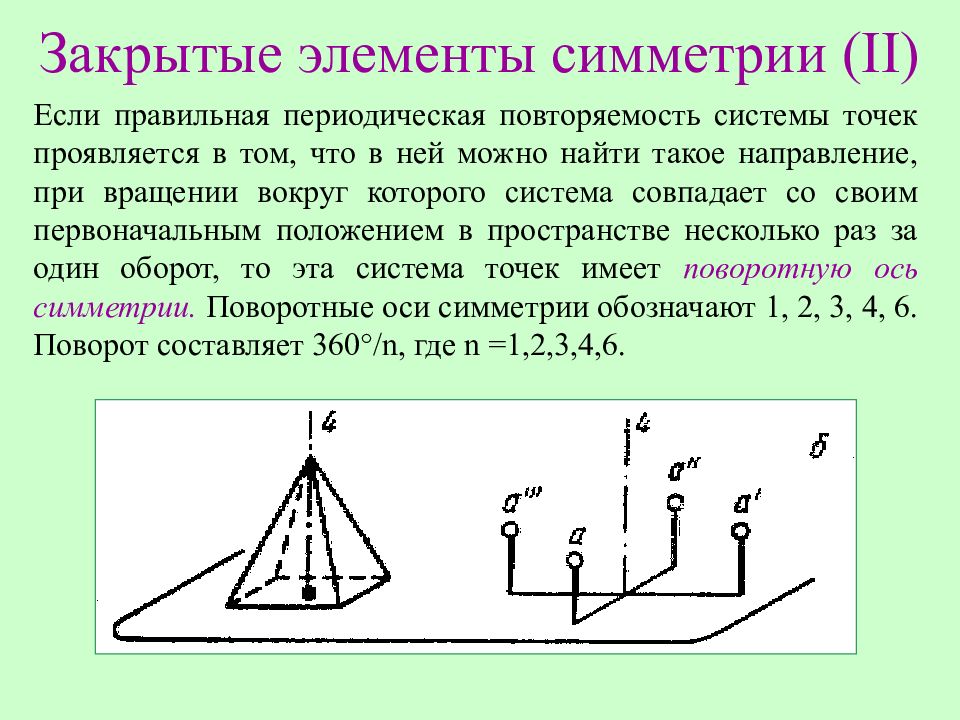
Если правильная периодическая повторяемость системы точек проявляется в том, что в ней можно найти такое направление, при вращении вокруг которого система совпадает со своим первоначальным положением в пространстве несколько раз за один оборот, то эта система точек имеет поворотную ось симметрии. Поворотные оси симметрии обозначают 1, 2, 3, 4, 6. Поворот составляет 360 ° / n, где n =1,2,3,4,6.
Слайд 19: Закрытые элементы симметрии ( III)
К аждая четная инвер - сионная ось есть в то же время и поворот - ная ось симметрии вдвое меньшего по - рядка. Противоп о лож - ное утверждение, справедливо не всегда. Если правильная периодичная повторяемость системы точек проявляется в том, что в ней можно найти такое направление, при вращении вокруг которого система попеременно совпадает то со своим отражением в точке, лежащей на этой оси, то со своим не отраженным первоначальным положением, то эта система точек считается имеющей инверсионную ось симметрии. Обозначения.
Слайд 20: Закрытые элементы симметрии ( IV)
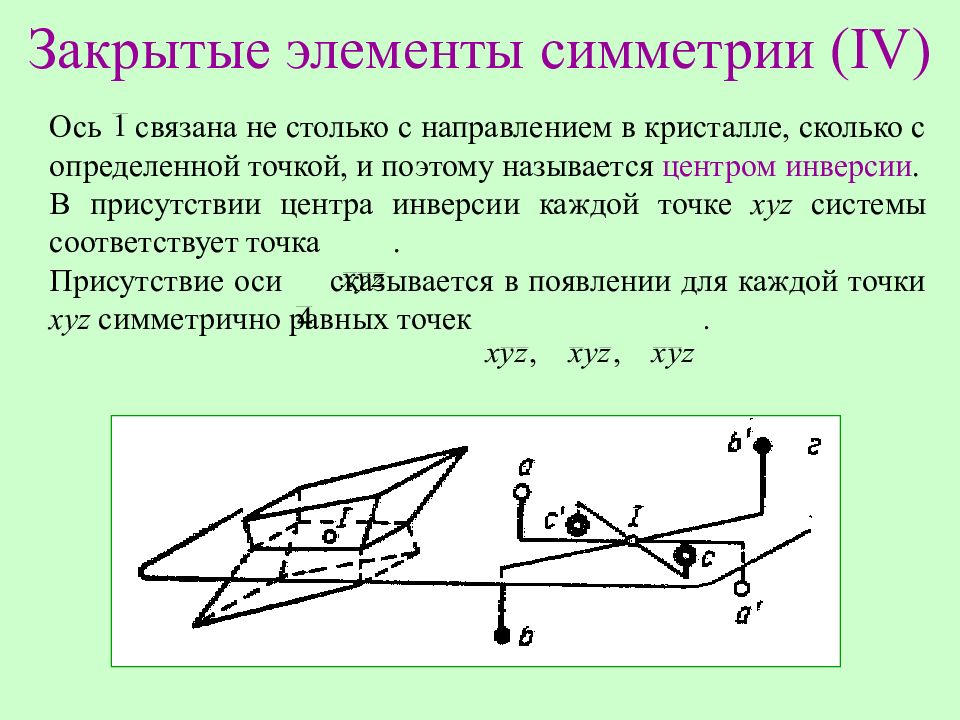
О сь связана не столько с направлением в кристалле, сколько с определенной точкой, и поэтому называется центром инверсии. В присутствии центра инверсии каждой точке ху z системы соответствует точка. Присутствие оси сказывается в появлении для каждой точки ху z симметрично равных точек.
Слайд 21: Закрытые элементы симметрии ( V)
Изложенные элементы симметрии были совместимы с трансляцией, но сами не содержали трансляции - они могут быть обнаружены в любом сколь угодно малом объеме кристалла вплоть до окружения одного узла. Они называются закрытыми элементами симметрии или элементами симметрии континуума и определяют большинство физических свойств кристалла и его облик. Однако для бесконечно протяженной пространственной решетки возможны и иные проявления правильной периодичной повторяемости мотива расположения точек системы за счет того, что смещение вдоль трансляции на целую трансляцию в бесконечно протяженной решетке есть тоже операция симметрии, приводящая систему точек в идентичное положение. Закрытые элементы симметрии ( V)
Слайд 22: Открытые элементы симметрии (I)
Е сли бесконечная правильная периодичная повторяемость системы точек проявляется в том, что она приходит в идентичное положение после сдвига и отражения в некоторой плоскости, то систему, точек с чи тают имеющей плоскость скользящего отражения. Открытые элементы симметрии (I) Плоскость скользящего отражения a
Слайд 23: Открытые элементы симметрии (II)
Если же бесконечная правильная периодичная повторяемость системы точек проявляется в том, что она приходит в идентичное положение после поворота вокруг некоторой оси и смещения вдоль этой оси, то систему точек считают имеющей винтовую ось симметрии. Винтовую ось обозначают комбинацией из двух цифр: первая, основная цифра, указывает порядок оси (угол поворота), вторая—цифровой индекс—указывает величину трансляции вдоль оси, выраженную в долях периода идентичности t вдоль этой оси. Например, символ 2 1 означает винтовую ось, при вращении вокруг которой на 180° и последующей трансляции на 1 / 2 периода идентичности вдоль этой оси решетка совмещается с исходным положением Плоскости скользящего отражения и винтовые оси носят название открытых элементов симметрии или элементов симметрии дисконтинуума.
Слайд 24
Сложение независимых закрытых элементов симметрии приводит к 32 точечным группам или классам симметрии. Классы симметрии в соответствии с присутствующими в них осями могут быть объединены в семь сингоний. Комбинируя элементы симметрии пространственных решеток, получают 230 систем расположения точек в пространственной трансляционной ячейке - 230 пространственных групп. Пространственной группой называется совокупность элементов симметрии, действующих на одну систему тра н сляций (ячейку Бравэ). Пространственные группы описывают, указывая тип ячейки Брав э и элементы симметрии, располагающиеся вдоль трансляционных направлений. Если в направлении трансляции располагается ось симметрии, а перпендикулярно к ней — плоскость симметрии, то символ пространственной группы записывают дробью, в числителе которой ставят обозначение оси, а в знаменателе — обозначение плоскости. Пример: структура Cu, NaCl, CaF 2 -
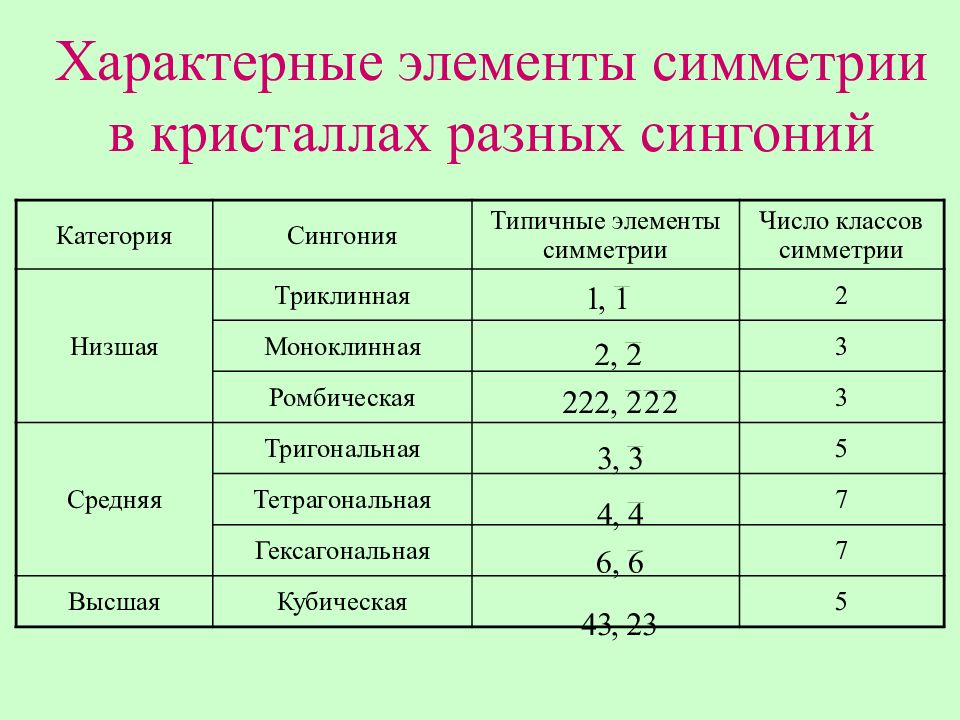
Слайд 26: Характерные элементы симметрии в кристаллах разных сингоний
Категория Сингония Типичные элементы симметрии Число классов симметрии Низшая Триклинная 2 Моноклинная 3 Ромбическая 3 Средняя Тригональная 5 Тетрагональная 7 Гексагональная 7 Высшая Кубическая 5
Слайд 27
По своему положению точки в элементарной ячейке могут быть расположены различно относительно элементов симметрии. Они занимают об щ ее положение, если находятся вне элементов симметрии, и частное, если лежат в каком-либо элементе симметрии. В последнем случае элемент симметрии, с которым они совпадают, на них не действует и от его реализации точка не переходит в новое положение - она многократно совпадает со своим первоначальным положением. Поэтому в ячейке различают точки по их кратности. Кратные точки заняты идентичными элементами структуры. Кратностью точки называют число положений точки, занимаемых ею в процессе реализации всех элементов симметрии, воздействующих на точку. С каждой пространственной группой в силу определенной симметрии решетки связаны вполне определенные координаты базиса при той или иной кратности точки. Пространственная группа кристалла определяет закон погасания интерференции.
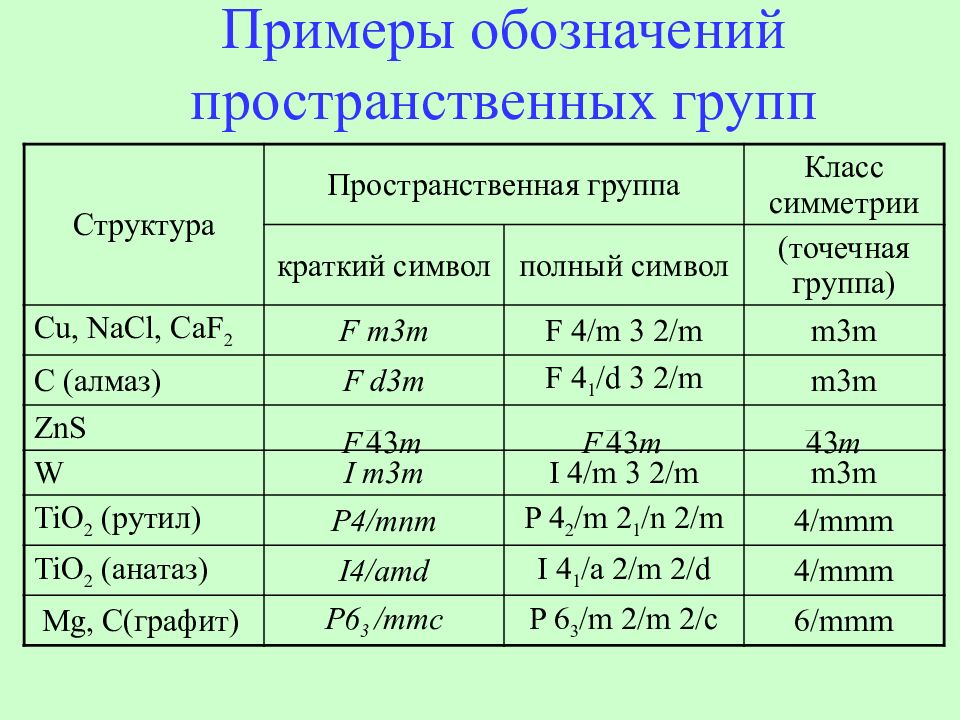
Слайд 28: Примеры обозначений пространственных групп
Структура Пространственная группа Класс симметрии краткий символ полный символ (точечная группа) Cu, NaCl, CaF 2 F m3m F 4/m 3 2/m m3m C ( алмаз) F d3m F 4 1 /d 3 2/m m3m ZnS W I m3m I 4/m 3 2/m m3m TiO 2 (рутил) P4/mnm P 4 2 /m 2 1 /n 2/m 4/mmm TiO 2 (анатаз) I4/amd I 4 1 /a 2/m 2/d 4/mmm Mg, C (графит) P6 3 /mmc P 6 3 /m 2/m 2/c 6/mmm
Слайд 29: Определение и обозначения структурных типов
Две структуры называются (конфигурационно) изотипными, если они принадлежат к одной и той же пространственной группе, имеют одинаковое число атомов в элементарной ячейке, занимающих одни и те же позиции Вайкоффа с одинаковыми или близкими позиционными координатами (х, у, z), а также одинаковые или близкие значения осевых отношений (с/а, a / b, b /с) и углов ( α, β, γ ) элементарных ячеек. Определение и обозначения структурных типов
Слайд 30
Конфигурационный изотипизм не обязательно означает подобие типов связи или возможность образования твердых растворов. Пример. Соединения TiC (с металлической и ковалентной связями) и КС1 (с ионной связью) изотипны кубической структуре NaCl (ионное соединение). Между TiC и NaCl нет никакой взаимной растворимости, но два хлорида образуют непрерывный ряд твердых растворов. Внутри ряда (Na, K)Cl постоянная решетки непрерывно меняется между a NaCl и а KCl. Структуры NaCl и КС1 можно назвать также кристаллохимически изотипными.
Слайд 31
Следует избегать использования термина « изоморфные » для изотипных структур. Слово « изоморфный » буквально означает « имеющий одинаковую форму кристалла ». Существует много соединений с различными кристаллическими структурами, которые образуют кристаллы одинаковой или близкой формы, И наоборот, форма кристаллов одного соединения может изменяться в зависимости от условий кристаллизации. Пример. NaCl обычно кристаллизуется в форме кубов. Если водный раствор этой соли имеет примесь мочевины CO ( NH 2 ) 2, то формируются октаэдры NaCl, a исходная кристаллическая структура сохраняется.
Слайд 32
Число неорганических соединений (исключая оксиды и галогениды) превышает 30 000, однако структурных типов, только около 3000. Среди них известны следующие: 53 структурных типа простых веществ; 127 типов бинарных эквиатомных соединений АВ (исключая политипы SiC, ZnS и GaSe); 137 типов бинарных соединений АВ 2 (исключая политипы CdI 2 ).
Слайд 33
Пример двух изотипных структур, изотипизм которых мог быть легко распознан по близким значениям координат атомов только после того, как структурные данные были приведены к стандартному виду: Опубликованные данные Стандартизованные данные CeCu 2, Imma KHg 2, Imma CeCu 2, Imma KHg 2, Imma a=4.425, b=7.057, c=7.475 Å a=8.10, b=5.16, c=8.77 Å a=4.425, b=7.057, c=7.475 Å a=5.16, b=8.10, c=8.77 Å Ce 4(e) 0 0,25 0,5377 K 4(e) 0 0,25 0,703 Ce 4(e) 0 0,25 0,5377 K 4(e) 0 0,25 0,547 Cu 8(h) 0 0,051 0,1648 Hg 8(h) 0,190 0,25 0,087 Cu 8(h) 0 0,051 0,1648 Hg 8(h) 0 0,06 0,163 Стандартизация данных для KHg 2 свелась к перестановке осей а и b и переносу начала координат.
Слайд 34: Обозначения структурных типов (I)
Химическая формула (химический символ) или название соединения (простого вещества), когда в основу положена в первую очередь последовательность отдельных атомов. Некоторые структурные типы были открыты независимо в разных местах, и поэтому им были даны различные названия. Разные названия структурных типов, приводимые в литературе, к сожалению, зависят от того, кто и чьи публикации читает. Пример. Тип ThO 2 Si 2 (на западе) = тип CeAl 2 Ga 2 (на востоке).
Слайд 35: Обозначения структурных типов (II)
Система обозначений по Strukturberichte (приложение к Zeitschrift f ü r Kristallographie). Обозначение структурного типа состоит из буквы и цифры. Буква условно обозначает состав, тогда как цифра является простым индексным числом без какой-либо дополнительной информации о структурных характеристиках. (Эти цифры соответствуют порядковым номерам, под которыми данные структурные типы приведены в справочнике Strukturberichte ). Такие обозначения все еще используются, однако после 1945 г. в журнале Structure Reports - преемнике журнала Strukturberichte - они не употреблялись.
Слайд 36: Примеры обозначения структурных типов по Stukturberichte
Буква Состав Обозначение (химическая формула или название) A элемент A1 (Cu), A2 (W), A3 (Mg), A4 ( алмаз ) B АВ Bl ( NaCl ), B 2 ( CsCl ), ВЗ (цинковая обманка), В4 ( в юртцит), В 8 ( NiAs ) C АВ 2 Cl ( CaF 2 ), C 14 ( MgZn 2 ), C 15 ( MgCu 2 ), C 36 ( MgNi 2 )
Слайд 37: Классификация структурных типов, основанная на пирсоновском коде
Пирсоновский код состоит из: строчной буквы латинского алфавита, обозначающей кристаллографическую систему: а - анортическая или триклинная, т - моноклинная, о - ромбическая (орторомбическая), t - тетрагональная, h - гексагональная и тригональная, с – кубическая; прописной буквы латинского алфавита, обозначающей тип решетки Бравэ: Р, S (для А-, В- или С-центровок), R, F, I ; числа соответствующего числу атомов в элементарной ячейке.
Слайд 38
Четырнадцать комбинаций из упомянутых выше букв отвечают 14 типам решеток Бравэ: aP-, тР -, mS-, oP-, oS-, oF-, oI-, tP-, tI-, hP-, hR-, cP-, cF-, cI- Примеры обозначений структурных типов кодом Пирсона: Ряд различных структурных типов может иметь один и тот же пирсоновский код, например С (алмаз) (Fd3m), ZnS (цинковая обманка) (F43m) и NaCl (Fm3m). Cu : cF4 Sm : hR9 W : cI2 ZnS : cF8 ZnS : hP4 (цинковая обманка) (вюрцит) Mg : hP2 As : hR6 C : cF8 NaCl : cF8 FeS 2 : cP12 (алмаз) (пирит)
Слайд 39: Классификация структурных типов, основанная на пространственной группе и последовательности Вайкоффа
Более тонкая классификация структурных типов базируется на пространственной группе (номере) и буквах принятых для обозначения позиций Вайкоффа, с последующим надстрочным числовым индексом (если он больше 1), который определяет, сколько раз используется данная позиция для заселения атомами. Для того чтобы правильно получить так называемую последовательность Вайкоффа, необходимо использовать только стандартизированные структурные данные.
Слайд 40: Позиции Вайкоффа
Группа: P63mc Общие позиции: 1 X, Y, Z 2 -X, -Y, Z+1/2 3 Y, X, Z+1/2 4 -Y, -X, Z 5 -X+Y, Y, Z 6 X-Y, -Y, Z+1/2 7 -X, -X+Y, Z+1/2 8 X, X-Y, Z 9 -Y, X-Y, Z 10 Y, -X+Y, Z+1/2 11 X-Y, X, Z+1/2 12 -X+Y, -X, Z Частные позиции Nr. Координаты Кратность Симметрия Символ Вайкоффа 1 d X,Y,Z 12 1 12d 2 c X,-X,Z 6.M. 6c 3 b 1/3,2/3,Z 2 3M. 2b 4 a 0,0,Z 2 3M. 2a
Последний слайд презентации: Структурная кристаллография
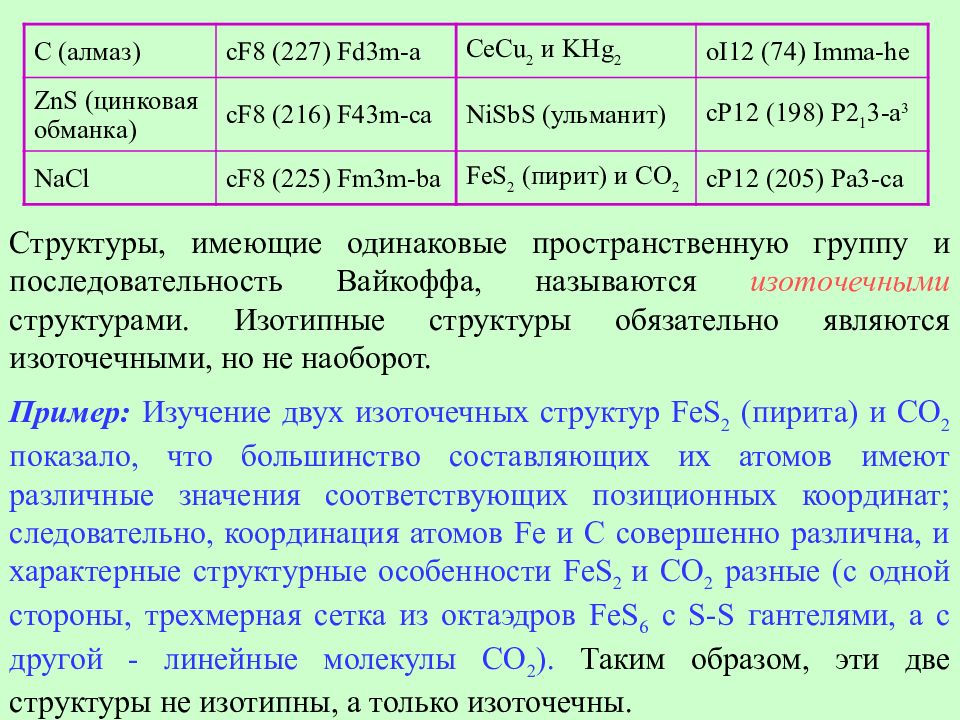
Структуры, имеющие одинаковые пространственную группу и последовательность Вайкоффа, называются изоточечными структурами. Изотипные структуры обязательно являются изоточечными, но не наоборот. Пример : Изучение двух изоточечных структур FeS 2 (пирита) и СО 2 показало, что большинство составляющих их атомов имеют различные значения соответствующих позиционных координат; следовательно, координация атомов Fe и С совершенно различна, и характерные структурные особенности FeS 2 и СО 2 разные (с одной стороны, трехмерная сетка из октаэдров FeS 6 с S-S гантелями, а с другой - линейные молекулы СО 2 ). Таким образом, эти две структуры не изотипны, а только изоточечны. С (алмаз) cF8 (227) Fd3m-a CeCu 2 и KHg 2 oI12 (74) Imma-he ZnS (цинковая обманка) cF8 (216) F43m-ca NiSbS (ульманит) cP12 (198) P2 1 3-a 3 NaCl cF8 (225) Fm3m-ba FeS 2 (пирит) и С O 2 cP12 (205) Pa3-ca