1 Глава1. Функция и ее предел
2
3
4 Задачники с решениями 1.Каплан И.А. Практические занятия по высшей математике.-Харьков: ХТУ, 1974.-ч.1. 2.Гурский Е.И., Домашов В.П. Руководство к решению задач по высшей математике.-Минск: ВШ, 1966.- ч.1. 3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в примерах и задачах. –М. : ВШ, 1980.-ч.1.
5
6
7
8
9
10
11
12
13
1 ). Четность функции (четная, нечетная, общего вида) 2). Периодичность функции 3). Монотонность функции (возрастающая, убывающая, неубывающая, невозрастающая) 4). Ограниченность функции (ограниченная сверху, ограниченная снизу, ограниченная) 14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
Вычислить предел функции: Решение. 68
Решение. 69
70
71
72
73
74
Решение. 75
76
Вычислить предел функции. 77
Вычислить предел функции: 78
79
80
81
82 Пример раскрытия неопределенности вида 0/0
83
Решение. 84
Решение. 85
86
87
Вычислить предел функции 88
Вычислить предел функции 89
90
Найти предел переменной: Решение. Замечая, что и применяя теоремы о пределах, найдём: Ответ: 2. 91
Задание. Найти предел последовательности : Решение. Замечая, что ( предел постоянной величины равен ей самой) и, применяя теоремы о пределах, найдем: 92
Найти предел: 93
94
Вычислить предел: Варианты ответов: 1). 2; 2). 4; 3). 1 /2 ; 4). 0. Укажите номер правильного ответа. 95
96
97
98
99
Вычислить предел: 100
Вычислить предел: 101
102
103
104
Вычислить предел функции. 105
Вычислить предел: 106
Вычислить предел функции. 107
Вычислить предел функции. 108
109
110
111
Вычислить предел функции: Варианты ответов: 1). 0; 2). 1; 3). 4). 2. Укажите номер правильного ответа. 112
113
114
Вычислить предел функции 115
Вычислить предел функции 116
117
118
119
120
121
122
1. 2. 3. 4. 5. 123
124
Пример1. Пример2. 125
Вычислить предел функции: 126
Вычислить предел функции, используя таблицу эквивалентных бесконечно малых. 127
Вычислить предел функции, используя таблицу эквивалентных бесконечно малых. 128
Вычислить предел функции: 129
Вычислить предел функции. 130
131
132
133
134
135
136
137
138
139
140
141
142
Пусть X = { x 0 } или X = ( a ; b ) или X = [ a ; b ]. 1) Сумма, разность и произведение конечного числа непрерывных на множестве X функций является функцией непрерывной на X. 2) Если функции f ( x ) и g ( x ) непрерывны на X и g ( x ) 0, x X, то частное f ( x )/ g ( x ) – непрерывная на множестве X функция. 3) Пусть f : X Y, : Y Z. Если f ( x ) непрерывна на X, ( x ) – непрерывна на Y, то сложная функция ( f ( x )) непрерывна на X. Свойства 1, 2, 3, следуют из свойств пределов функций. 143
СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 4) Основные элементарные функции непрерывны всюду в своей области определения. Если функция непрерывна всюду в области определения, то ее называют непрерывной. 5) Всякая элементарная функция непрерывна в каждой точке, в которой она определена (следствие свойств 1– 4). 144
145
146
147
148
Свойства функций непрерывных на отрезке непрерывных функций 149
150
151
152
153
154
Исследовать на непрерывность функцию Решение. 155
156
157
158
Исследовать на непрерывность функцию Решение. 159
160
161 СПАСИБО ЗА ВНИМАНИЕ
Пусть функция определена на множестве и - предельная точка этого множества. Возможны 3 случая : 1) Предел А существует, в то время как в точке не определена. 2) Предел А существует, существует и, но 3) Предел А существует и существует, причем 162 .
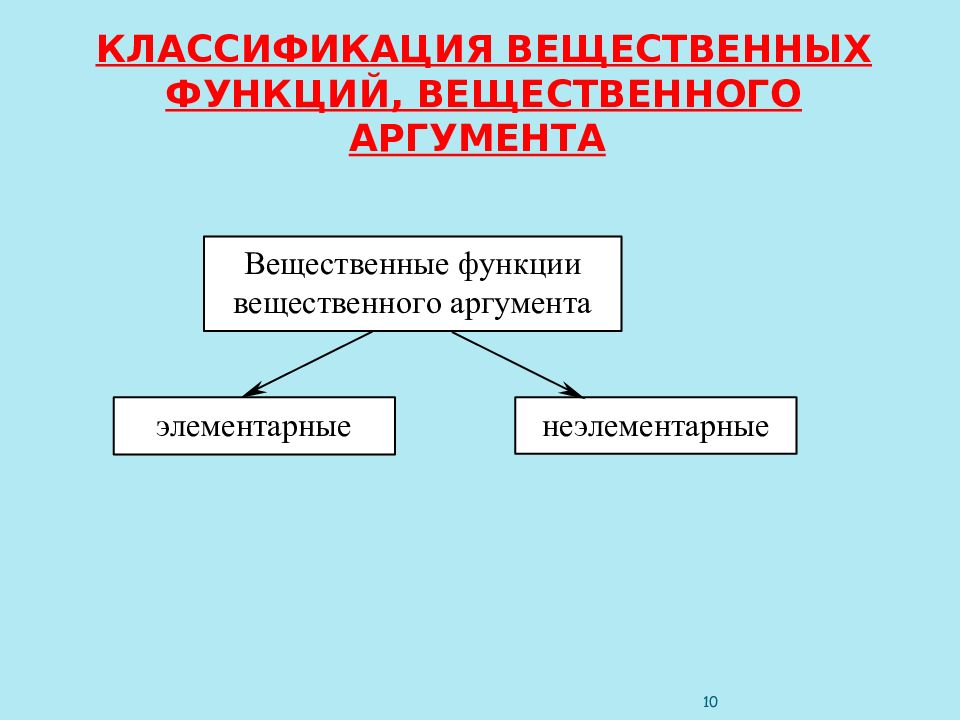
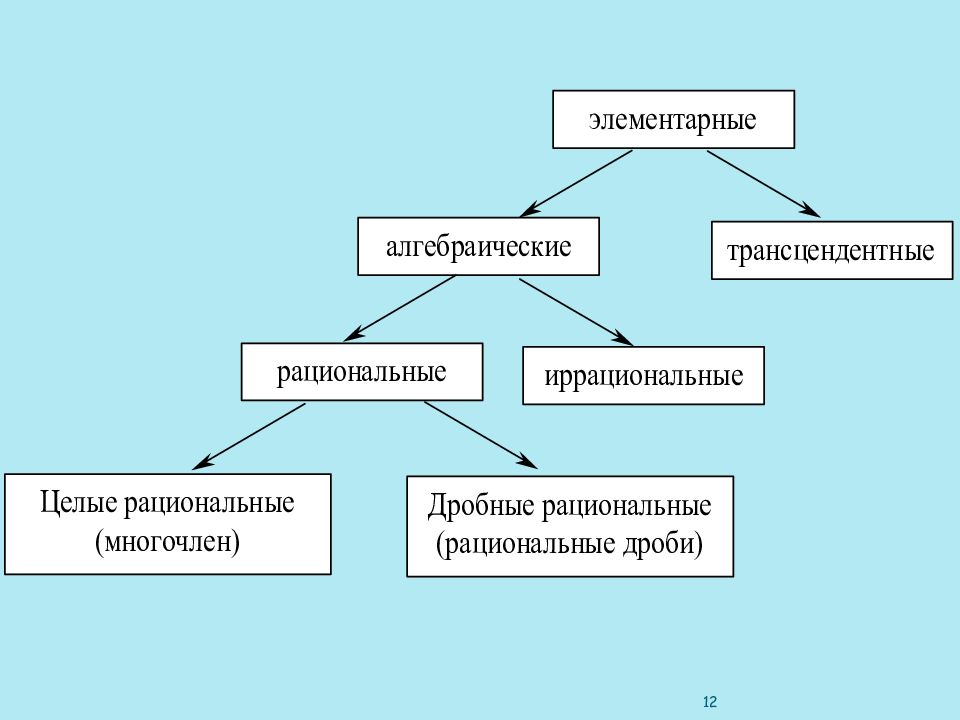
Элементарные функции делят на два класса: алгебраические и трансцендентные. ОПРЕДЕЛЕНИЕ. Функция называется алгебраической, если ее значение можно получить из аргумента и действительных чисел с помощью конечного числа алгебраических операций (т.е. сложения, вычитания, умножения, деления) и возведения в степень с рациональным показателем. Функция, не являющаяся алгебраической, называется трансцендентной. Алгебраические функции делят на рациональные и иррациональные. ОПРЕДЕЛЕНИЕ. Алгебраическая функция называется рациональной, если среди действий, которые производятся над независимой переменной, отсутствует извлечение корня. Функция не являющаяся рациональной называется иррациональной. Рациональные функции бывают двух видов: целые рациональные (многочлены), где ; дробные рациональные (рациональные дроби) 163
ОПРЕДЕЛЕНИЕ. Элементарной функцией называется функция, которая может быть задана одной формулой y = f ( x ), где f ( x ) – выражение, составленное из основных элементарных функций и действительных чисел с помощью конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ: 1) степенные: y = x r ( r ℝ ) 2) показательные: y = a x ( a > 0, a 1) 3) логарифмические: y = log a x ( a > 0, a 1) 4) тригонометрические: y = sin x, y = cos x, y = tg x, y = ctg x 5) обратные тригонометрические: y = arcsin x, y = arccos x, y = arctg x, y = arcctg x 164
Аналитический способ заключается в том, что зависимость между переменными величинами задаётся с помощью формулы, указывающей, какие действия надо выполнить над аргументом, чтобы получить соответствующее ему значение функции. При этом функция может быть задана как одной формулой, например, так и несколькими формулами, например Табличный способ заключается в том, что зависимость между переменными задают с помощью таблицы. Хорошо известны, например, таблицы логарифмов, тригонометрических функций. Графический способ состоит в том, что соответствие между переменными х и у задаётся с помощью графика функции. Графиком функции y = f ( x ) называется множество всех точек ( х, у ) плоскости XOY, координаты которых связаны соотношением y = f ( x ). Так, графики вышеназванных функций: f ( x ) и g ( x ) 165
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ 1) аналитический : а) явное задание (т.е. формулой y = f ( x ) ) б) неявное задание (т.е. с помощью уравнения F ( x, y )=0 ). 2) табличный; 3) графический; ОПРЕДЕЛЕНИЕ. График о м функции y = f ( x ) называется геометрическое место точек плоскости с координатами ( x ; f ( x )). График функции y = f ( x ) будем также называть «кривой y = f ( x )». 4) словесный. 166
ПОНЯТИЕ ФУНКЦИИ Пусть X, Y – множества произвольной природы. ОПРЕДЕЛЕНИЕ(функции). Если x X поставлен в соответствие единственный элемент y Y, т о говорят, что на множестве X задана функция ( отображение ) с множеством значений Y. Записывают: f : X Y, y = f ( x ) (где f – закон, осуществляющий соответствие) Называют: X – область (множество ) определения функции x ( x X ) – аргумент ( независимая переменная ) Y – область ( множество ) значений y ( y Y ) – зависимая переменная ( функция ) 167
