Рациональные уравнения и неравенства 10 классы
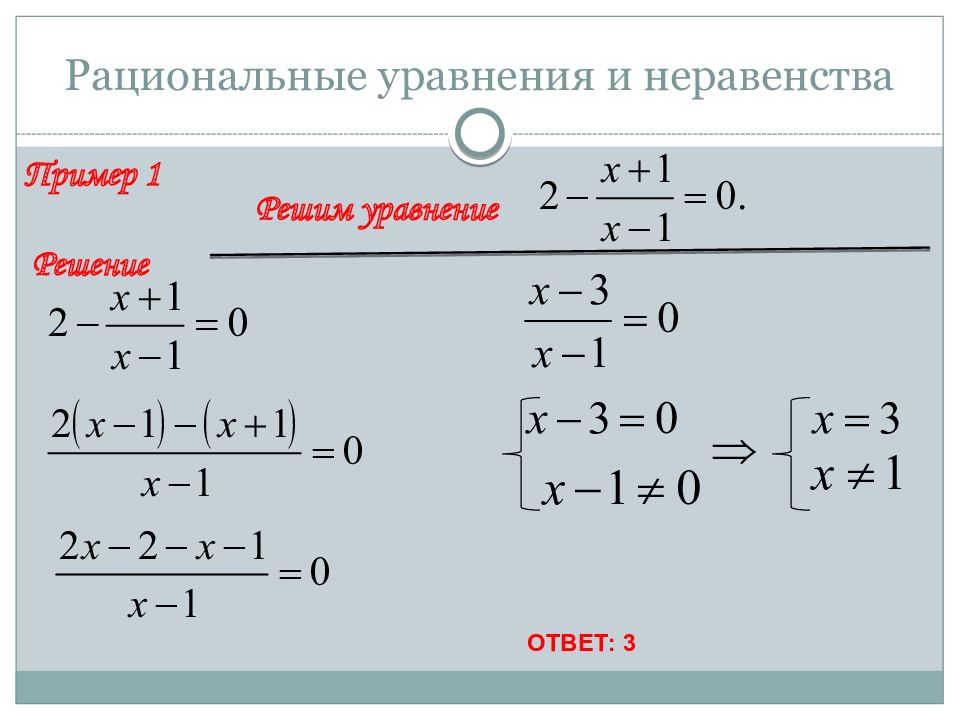
Пример 1 Решим уравнение Решение ОТВЕТ: 3
Пример 2 Решим уравнение Решение х – 3 х + 2 (х + 2)(х – 3)
Пример 2 Решим уравнение Решение
Пример 2 Решим уравнение Решение Исходное уравнение не имеет корней, так как числитель равносильного уравнения не имеет корней. ОТВЕТ: корней нет.
Для решения рационального уравнения надо перенести все его члены в левую часть, затем, применяя правила сложения и вычитания алгебраических дробей, записать левую часть как алгебраическую дробь и решить полученное уравнение. Правило Замечание Отклонение от высказанного правила может привести к потере корней или к приобретению посторонних корней данного уравнения.
Например х - 3 Х равное 3 обращает знаменатель в нуль, значит уравнение корней не имеет. Однако, если бы мы отклонились от правила, сократили дробь в левой части уравнения на (х – 3), Но х=3 не является корнем исходного уравнения – при х=3 левая его часть превращается в выражение, не имеющее смысла. Следовательно при таком «способе решения» мы получили посторонний корень.
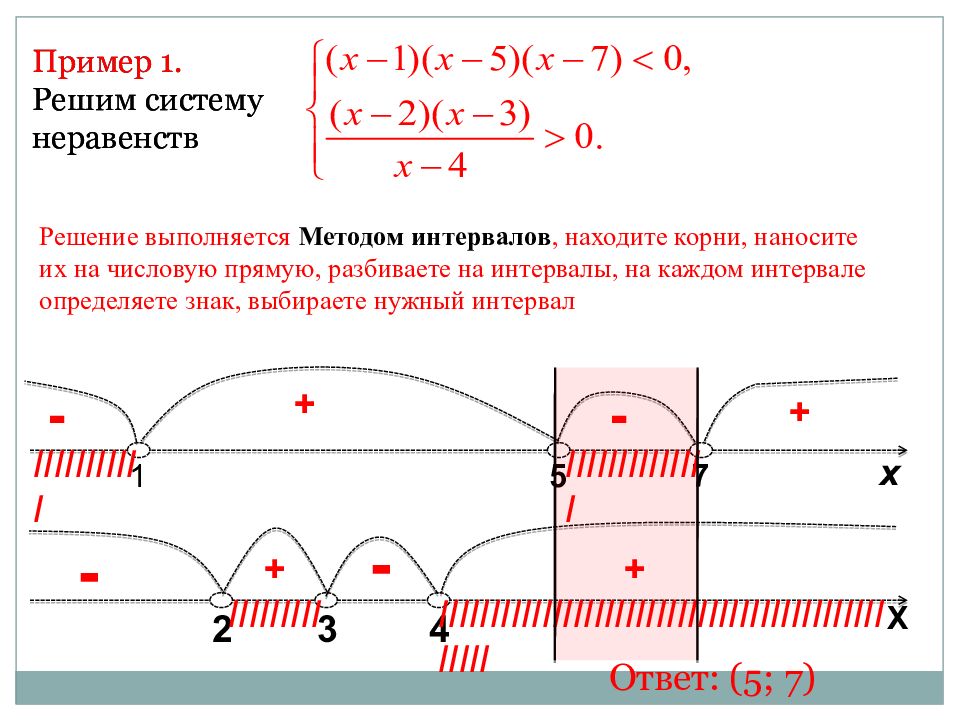
Пример 1. Решим систему неравенств Решение выполняется Методом интервалов, находите корни, наносите их на числовую прямую, разбиваете на интервалы, на каждом интервале определяете знак, выбираете нужный интервал х 1 5 7 + + - - IIIIIIIIIII IIIIIIIIIIIIII X 2 3 4 + + - - IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIII Ответ: (5; 7)
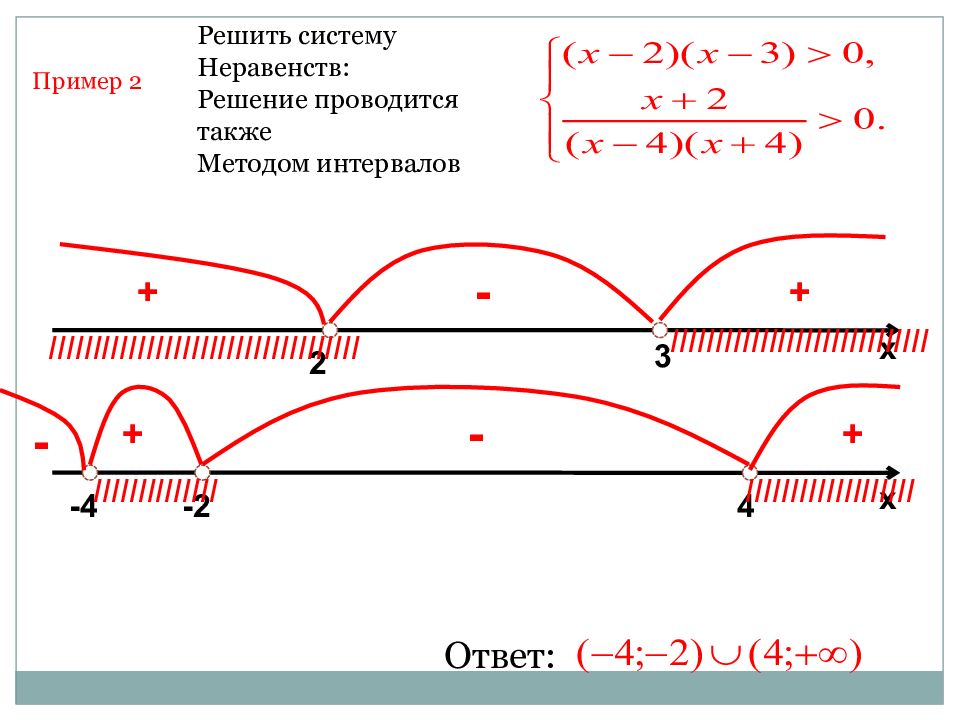
Решить систему Неравенств: Решение проводится также Методом интервалов х х 2 3 + - + IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII Ответ: IIIIIIIIIIIIIIIIIIIIIIIIIIIII -4 -2 4 + - + - IIIIIIIIIIIIII IIIIIIIIIIIIIIIIIII Пример 2
Пример 3 Решить систему неравенств: Решение. Перенеся все слагаемые в левую часть каждого из неравенств исходной системы, перепишем ее в виде
28.04.2020 Пример 3 Продолжение х -1 0 1 + - + - + IIIIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIIIIIIIII X -1,5 + - IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII Ответ:
Повторить п.2.6, п. 2.9 Решить: 1гр. №51( а,б ),97( а,б ) 2 гр. №52( а,б ), №97( в,г )
