Расстояние от точки до прямой. Расстояние между параллельными прямыми. . .
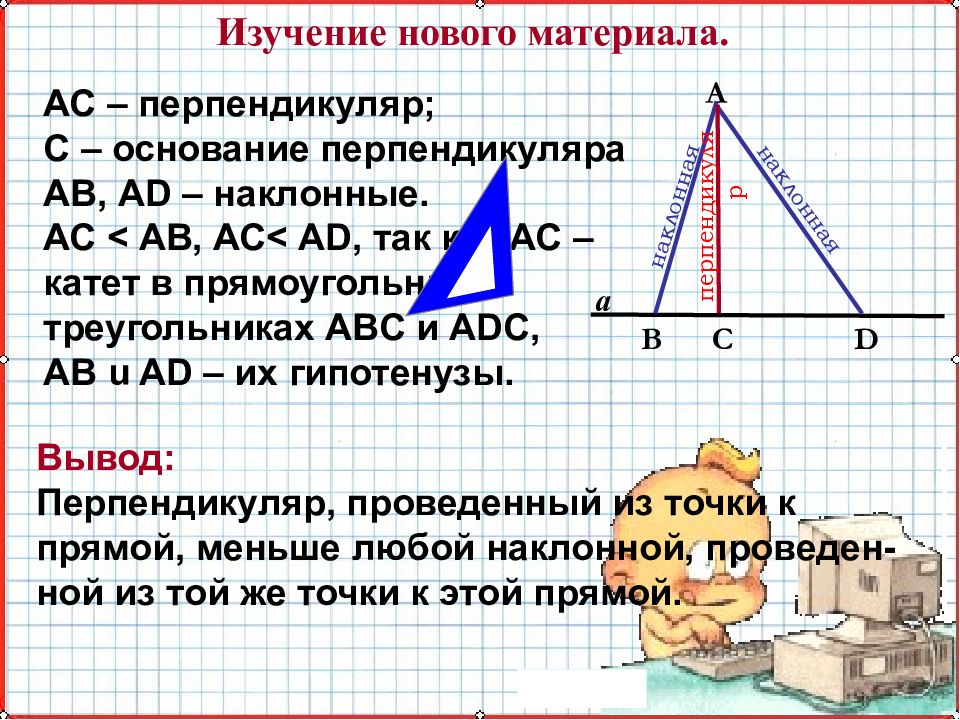
Изучение нового материала. а С D В А наклонная перпендикуляр наклонная АС – перпендикуляр; С – основание перпендикуляра АВ, AD – наклонные. АС < АВ, АС< AD, так как АС – катет в прямоугольных треугольниках ABC и ADC, AB u AD – их гипотенузы. Вывод: Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведен-ной из той же точки к этой прямой.
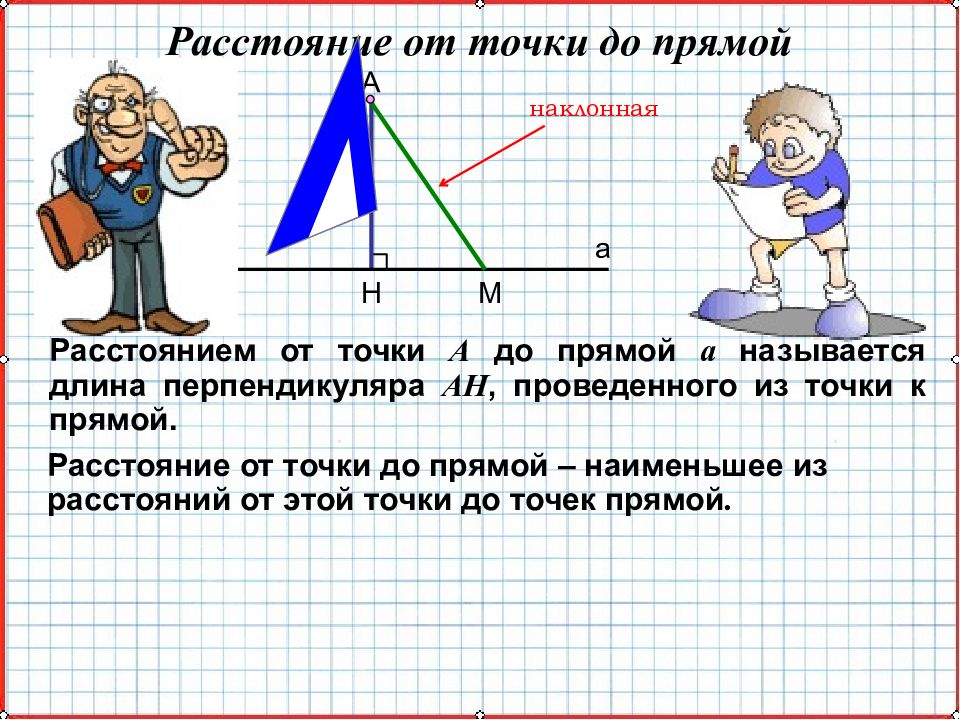
Расстоянием от точки A до прямой a называется длина перпендикуляра AH, проведенного из точки к прямой. Расстояние от точки до прямой – наименьшее из расстояний от этой точки до точек прямой. Расстояние от точки до прямой A H M a наклонная
Расстояние от точки одной из двух параллельных прямых до другой прямой одинаково для всех точек. Расстояние между параллельными прямыми B A b Если a || b, AB b, MN b (см. рис.), то AB = MN. a Если MN b, то MN a. N M ~ Δ ABN = Δ NMA (по гипотенузе и острому углу) Доказательство Следовательно, AB = MN, ч.т.д. Обратно: все точки по одну сторону от данной прямой, удаленные от нее на данное расстояние, лежат на параллельной прямой.
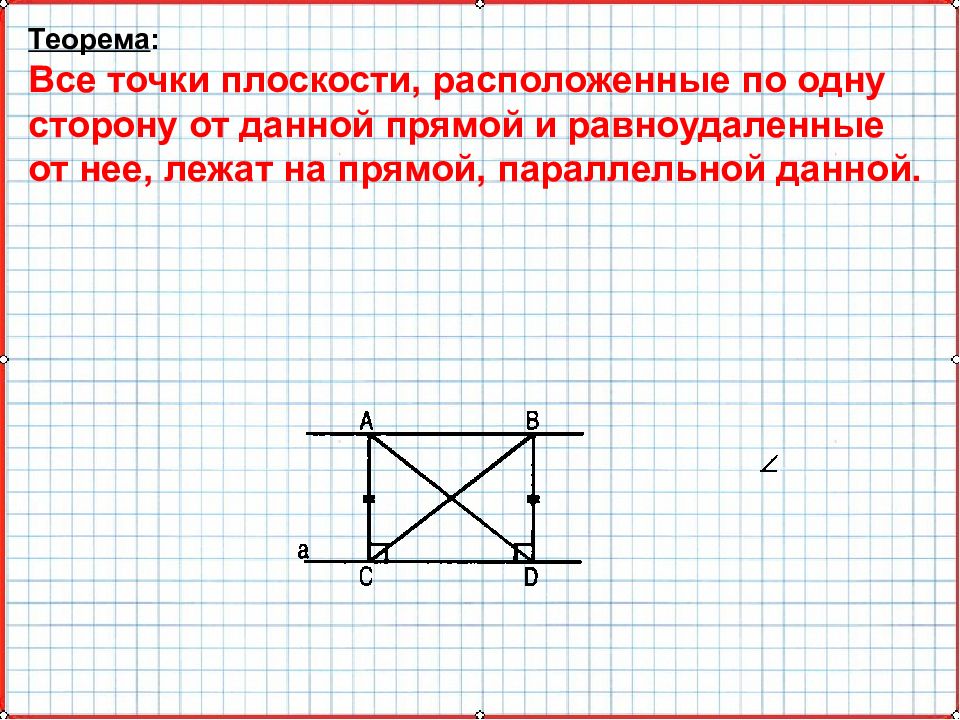
Теорема : Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой, параллельной данной.
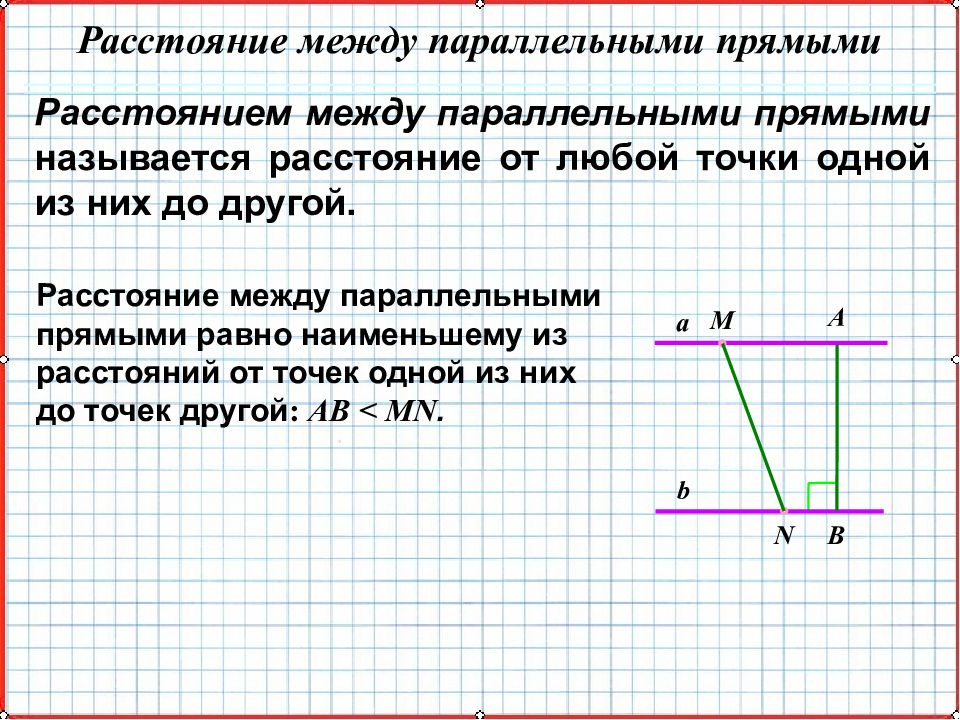
Расстоянием между параллельными прямыми называется расстояние от любой точки одной из них до другой. Расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной из них до точек другой : AB < MN. Расстояние между параллельными прямыми B A b a M N
UROKI MATEMATIKI.RU Игорь Жаборовский © 2011 На этом свойстве основано устройство инструмента, называемого рейсмусом. Рейсмус используется в столярном деле для разметки на поверхности деревянного бруска прямой, параллельной краю бруска. При передвижении рейсмуса вдоль края бруска металлическая игла прочерчивает отрезок прямой, параллельный краю бруска.
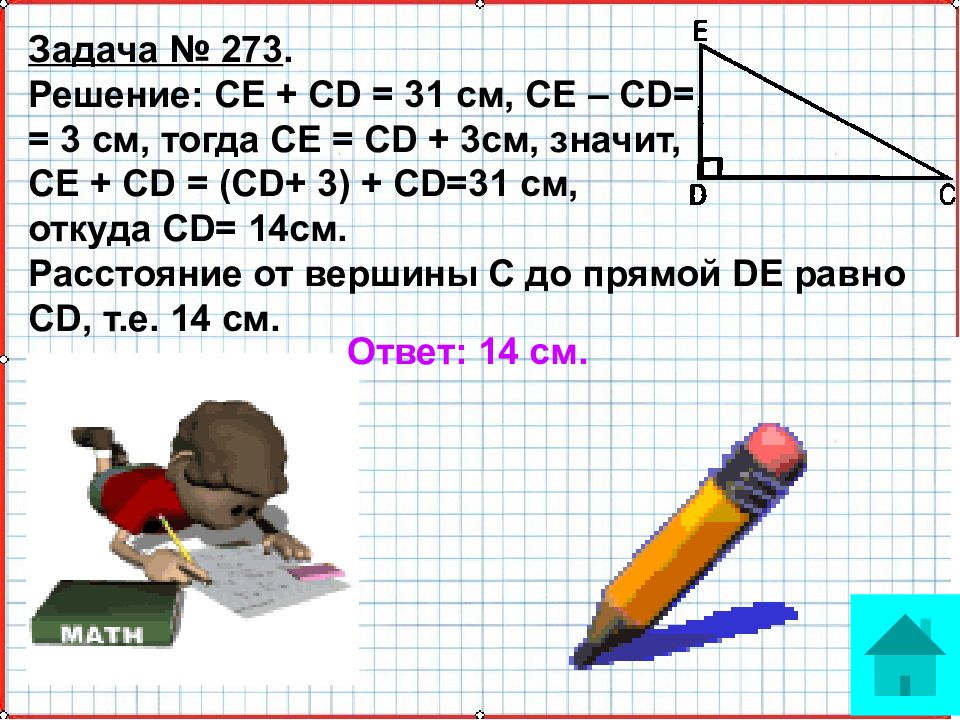
Задача № 273. Решение: СЕ + CD = 31 см, СЕ – CD= = 3 см, тогда СЕ = CD + 3см, значит, СЕ + CD = (CD+ 3) + CD=31 см, откуда CD= 14см. Расстояние от вершины С до прямой DE равно CD, т.е. 14 см. Ответ: 14 см.
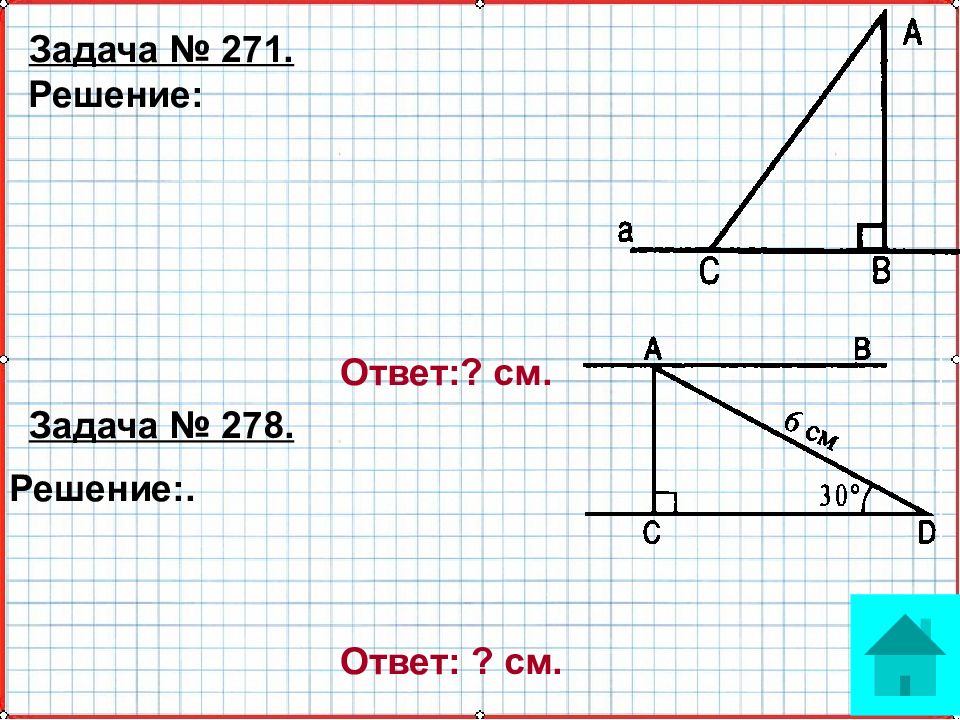
Решение: О - середина АВ, тогда АО=BO. AD и BC – расстояние от концов от- резка АВ до прямой a (AD а, ВС a). ∆ AOD = ∆ ВОС по гипотенузе и острому углу (АО = OB, AOD = ВОС как вертикальные), тогда AD = СВ, то есть концы отрезка АВ равноудалены от прямой а. Задача № 276.
Решение: Решение:. Задача № 278. Задача № 271. Ответ: ? см. Ответ:? см.
Доказать: СМ- высота Задача № 275.
