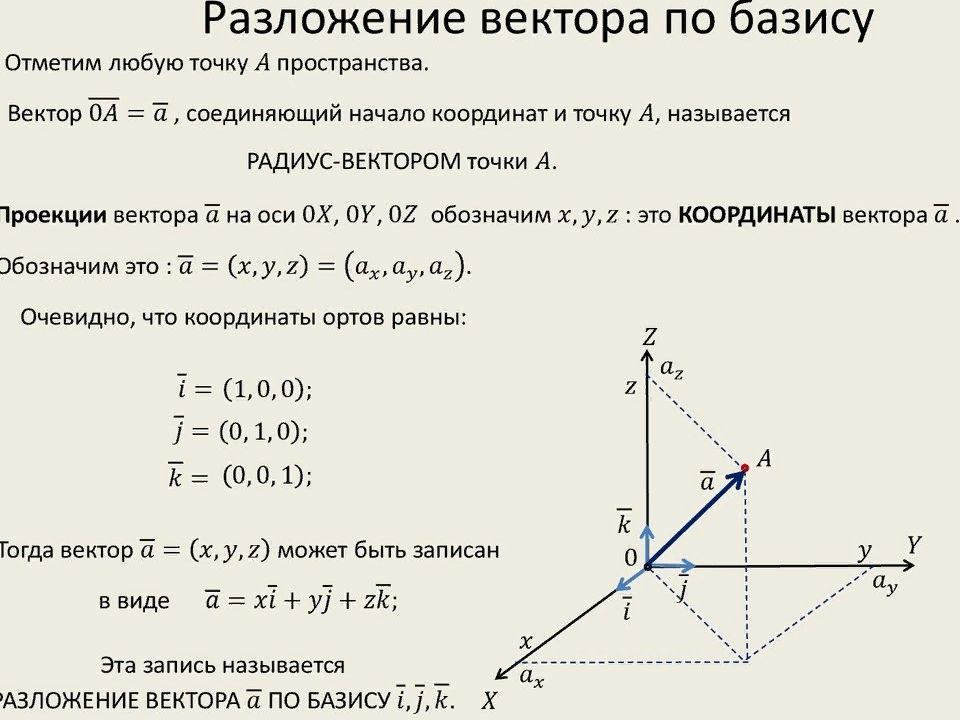
Первый слайд презентации: Разложение вектора по направлениям осей координат
Слайд 2
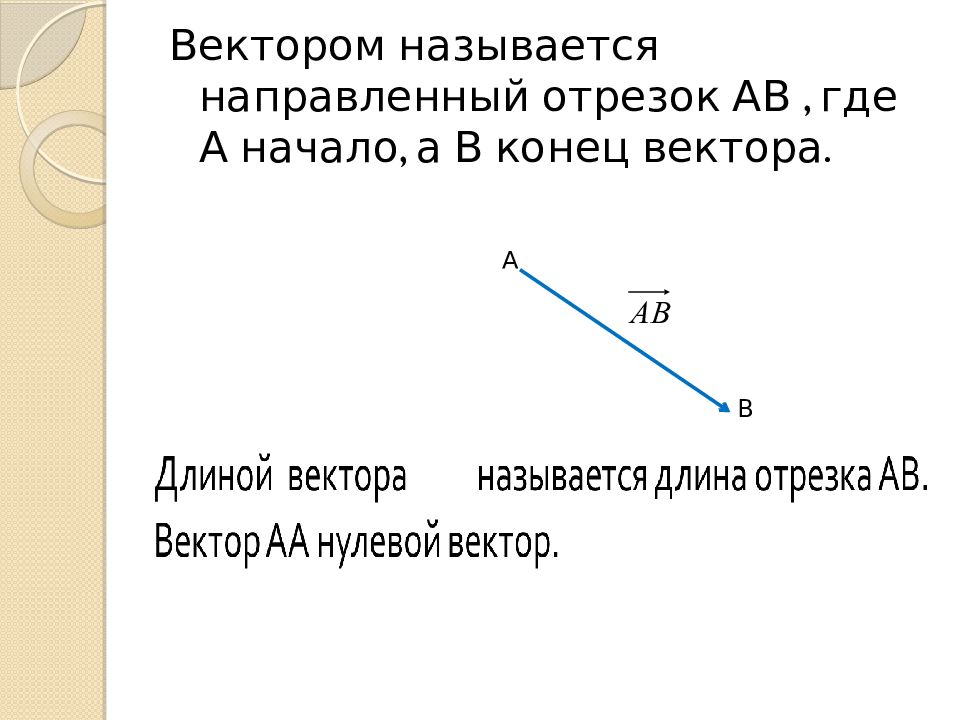
Вектором называется направленный отрезок АВ, где А начало, а В конец вектора. А В
Слайд 4
Векторы называются коллинеарными, если они лежали на одной прямой или параллельных прямых. Векторы и сонаправленные. Векторы и противоположно направленные.
Слайд 5
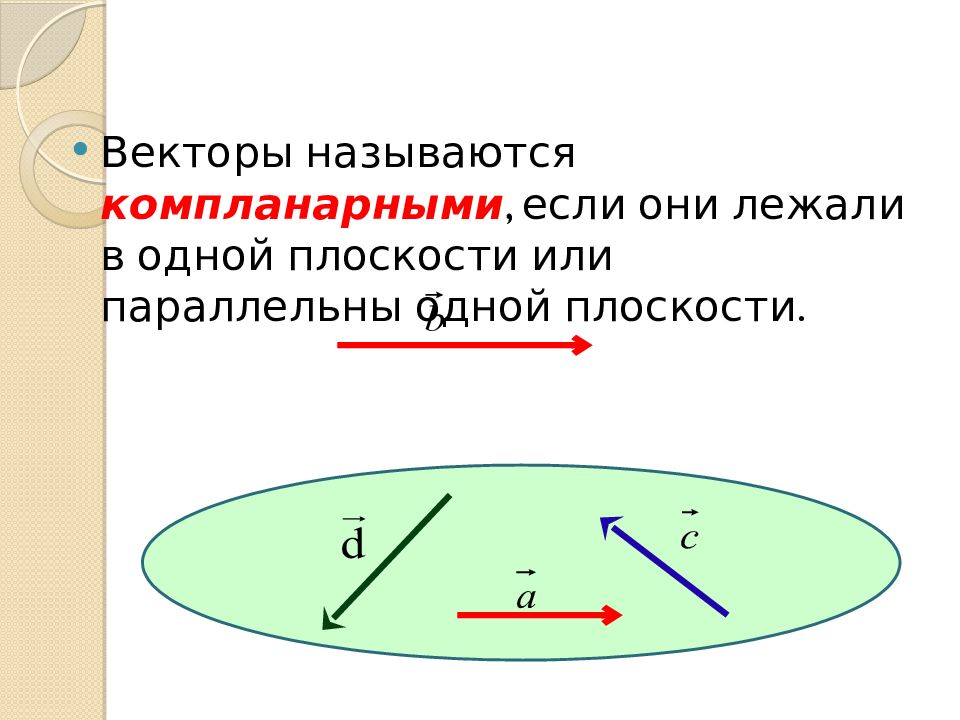
Векторы называются компланарными, если они лежали в одной плоскости или параллельны одной плоскости.
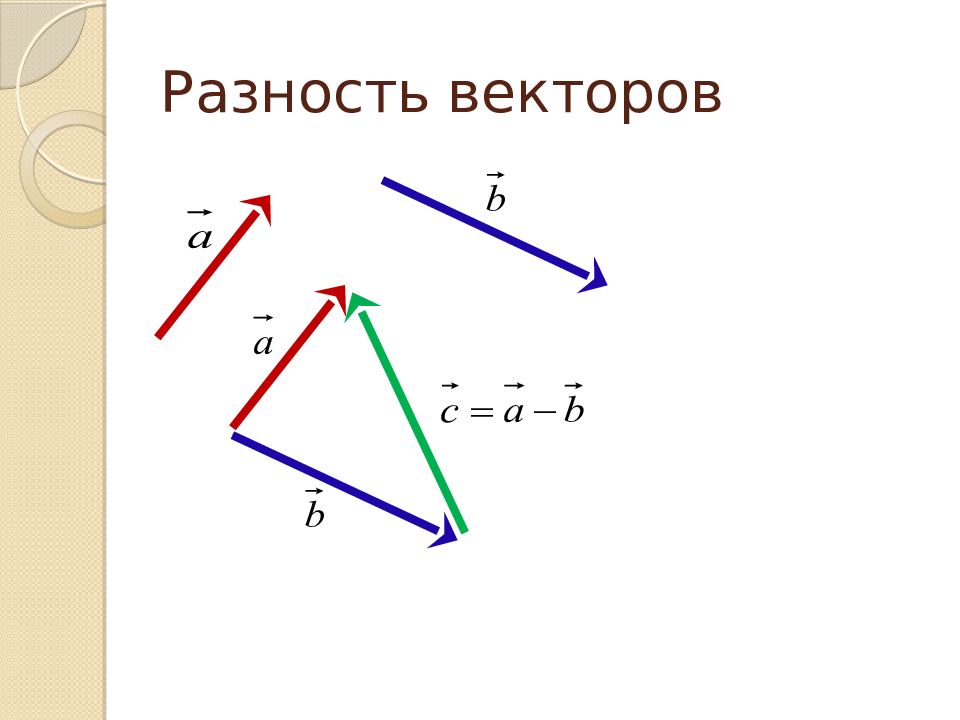
Слайд 8: Разность векторов
Слайд 9: Умножение вектора на число
Произведением вектора на действительное число λ называется вектор, коллинеарный вектору , имеющий длину и направление, совпадающее с направлением вектора, если λ >0, и противоположное вектору, если λ <0
Слайд 10: Условие коллинеарности векторов
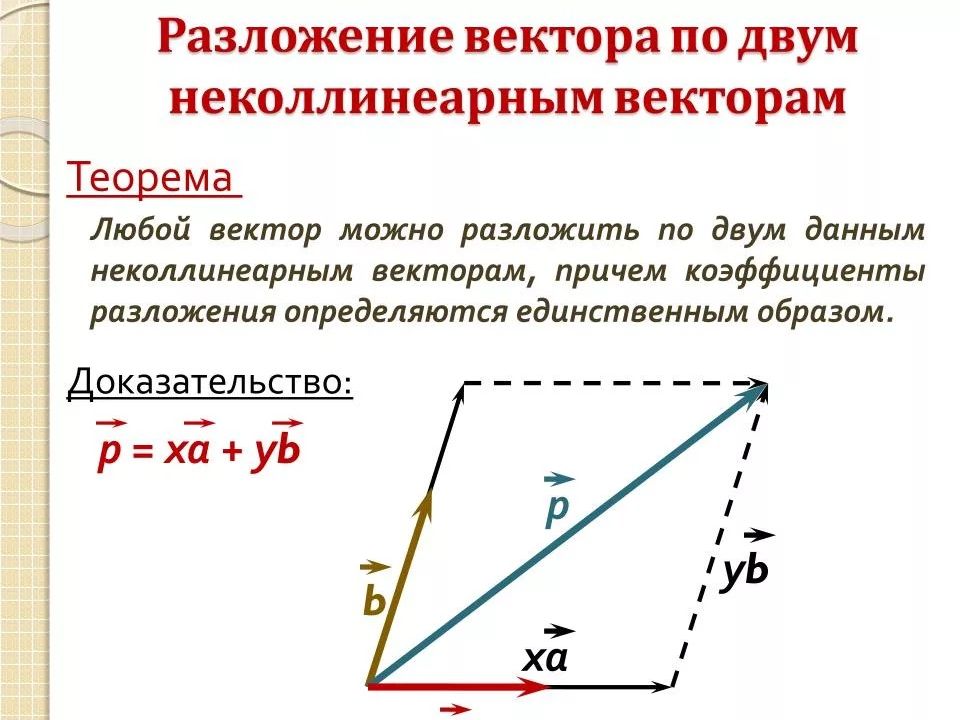
Два вектора коллинеарны тогда и только тогда, когда один из них может быть представлен в виде линейной комбинации другого.
Слайд 15: Выводы
Вектор это направленный отрезок или параллельный перенос. Над векторами можно проводить операции сложения, вычитания, умножения на число. Вектор можно представлять через другие векторы
Слайд 19: Решите самостоятельно:
Дан вектор + Запишите координаты векторов и вычислите его длину. Дан вектор {5;-1;2}. Запишите разложение этих векторов по координатным векторам ,,. Дан вектор {3;-2;1}. Запишите разложение этих векторов по координатным векторам,,.