Координаты вектора Л.С. Атанасян "Геометрия 10-11" Савченко Е.М., учитель математики, МОУ гимназия №, г. Полярные Зори, Мурманской обл.
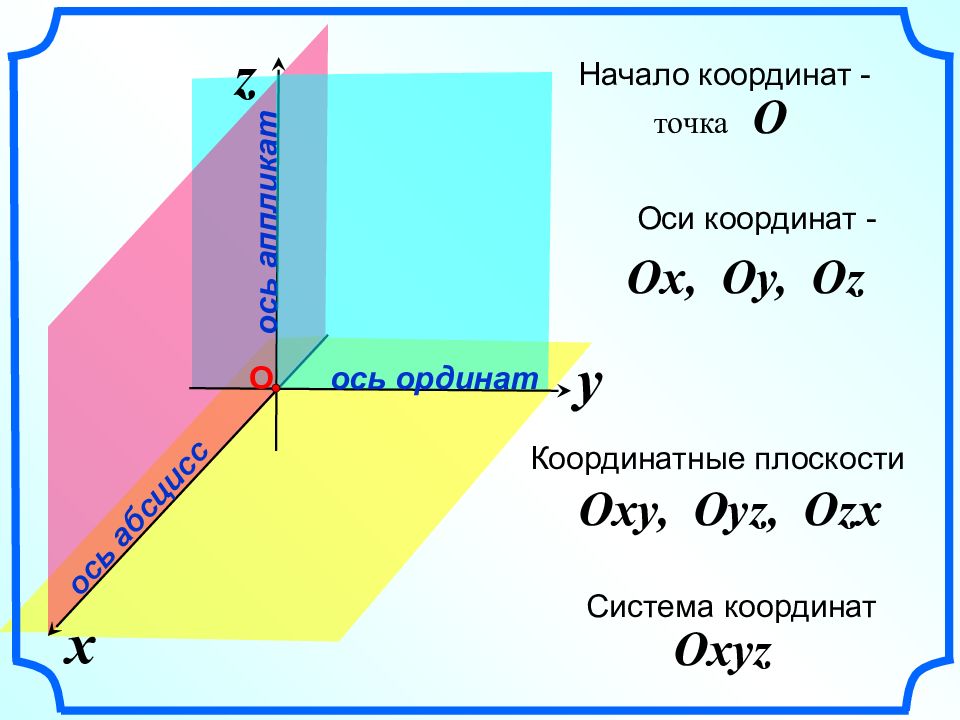
x ось абсцисс z ось аппликат Оси координат - Ox, Oy, Oz Начало координат - точка O Координатные плоскости Oxy, Oyz, Ozx Система координат Oxyz y ось ординат О
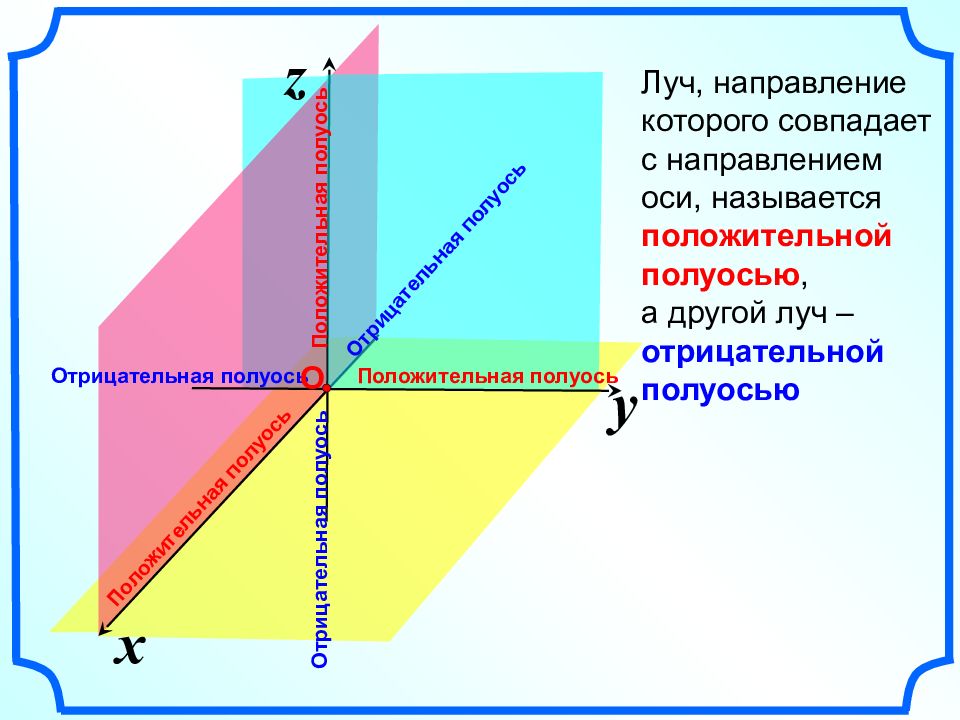
x z y Отрицательная полуось Положительная полуось О Положительная полуось Отрицательная полуось Положительная полуось Отрицательная полуось Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью
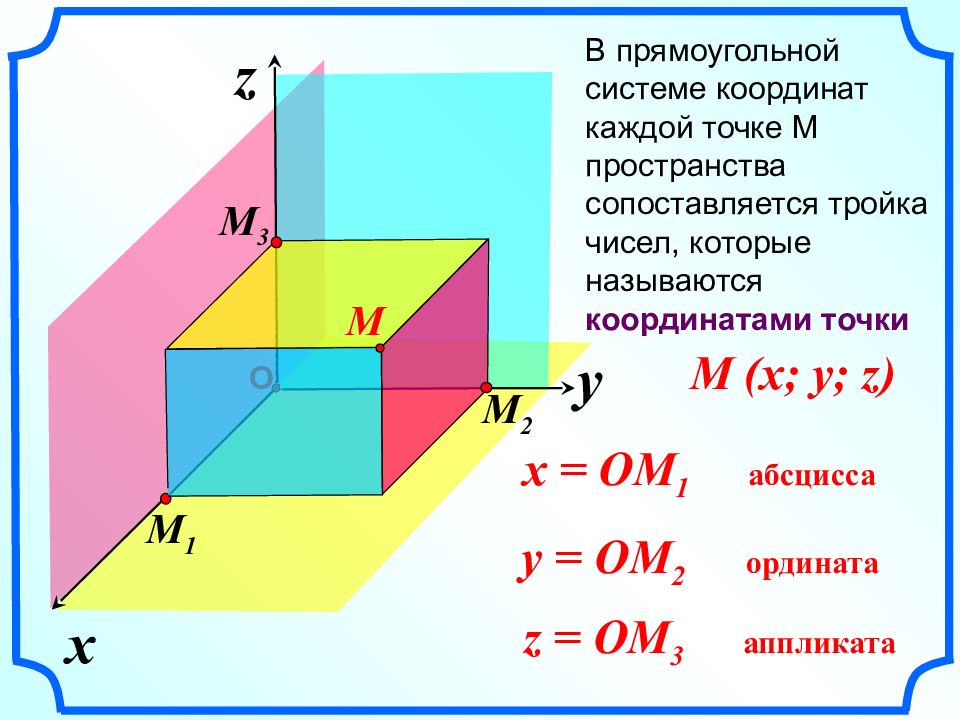
x z В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются координатами точки y О M (x; y; z) x = OM 1 абсцисса y = OM 2 ордината z = OM 3 аппликата M 1 M 3 M 2 M
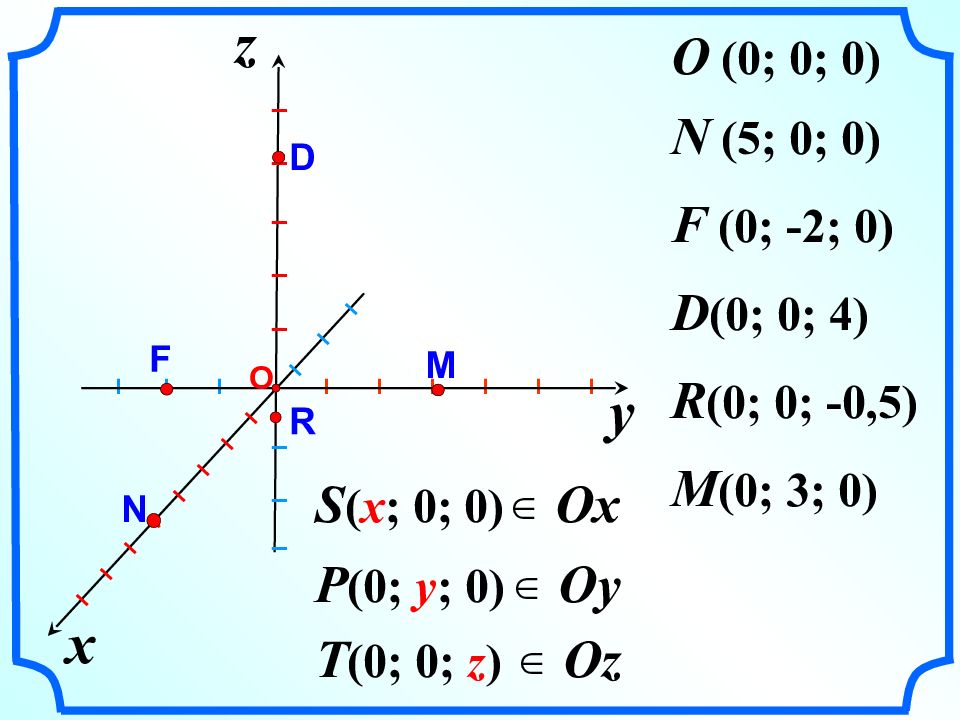
y x z O (0; 0; 0) I I I I I I I I I О N (5; 0; 0) I I I I I I I I I I I I I I I I I I I N F D R F (0; -2; 0) D (0; 0; 4) R (0; 0; -0,5) M M (0; 3; 0) S ( x ; 0; 0) P (0; y ; 0) T (0; 0; z ) Ox Oy Oz
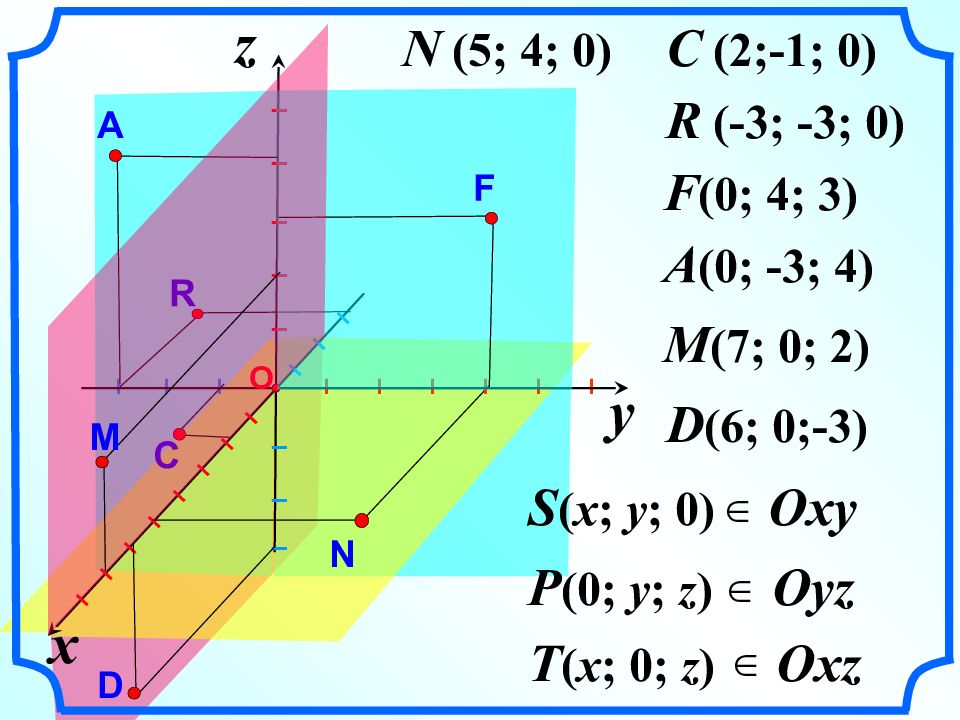
z N ( 5 ; 4 ; 0) C (2;-1; 0) I I I I I I I I I I I R (-3; -3; 0) F (0; 4; 3) A (0; -3; 4) M (7; 0; 2) S ( x ; y ; 0) P (0; y ; z ) T ( x ; 0; z ) Oxy Oyz Oxz y R N I I I I I I I I I О I I I I I I I I F D x C A D (6; 0;-3) M
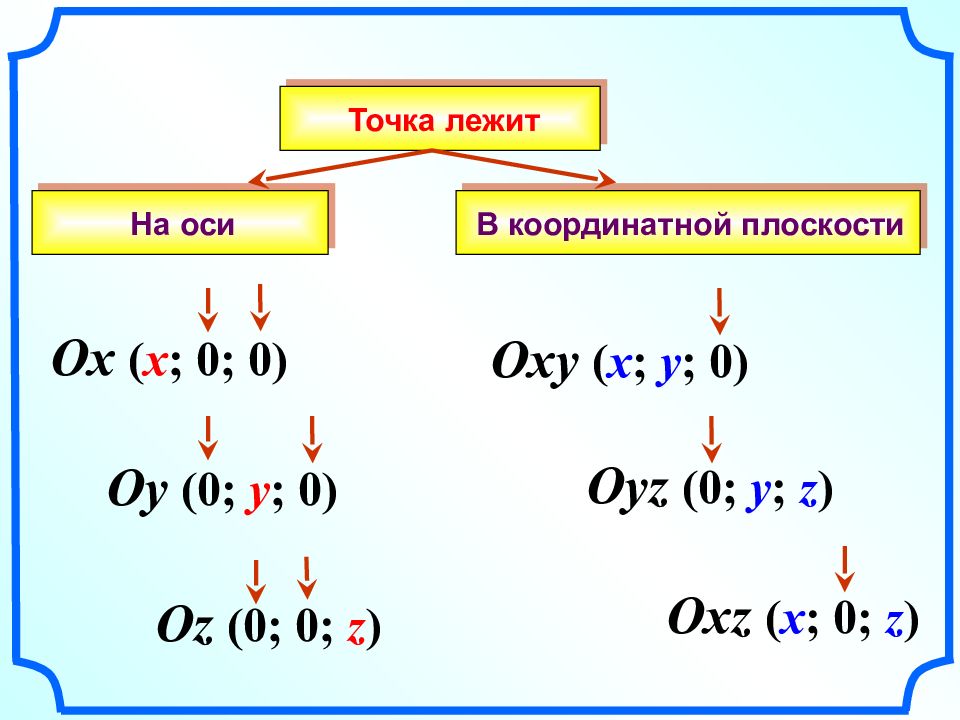
В координатной плоскости Oxy ( x ; y ; 0) Oyz (0; y ; z ) Oxz ( x ; 0; z ) Ox ( x ; 0; 0) Oy (0; y ; 0) Oz (0; 0; z ) На оси Точка лежит
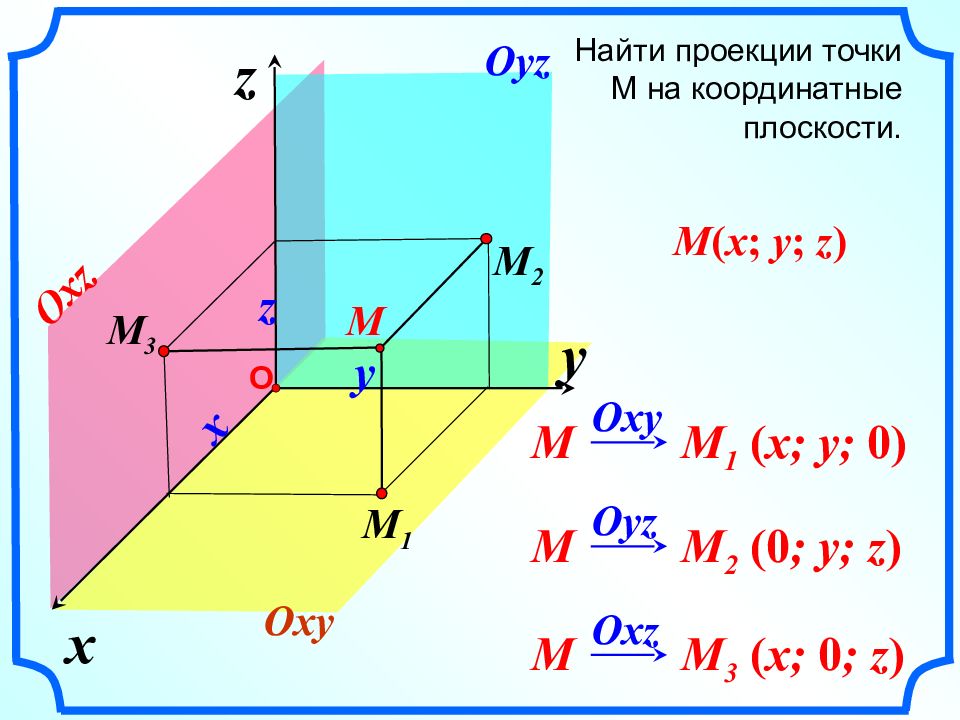
x z Найти проекции точки М на координатные плоскости. y О M M 1 M 2 M 3 M M 1 ( x; y; 0) Oxy M M 2 ( 0 ; y; z ) Oyz M M 3 ( x; 0 ; z ) Oxz x y z Oxy Oyz Oxz M ( x ; y ; z )
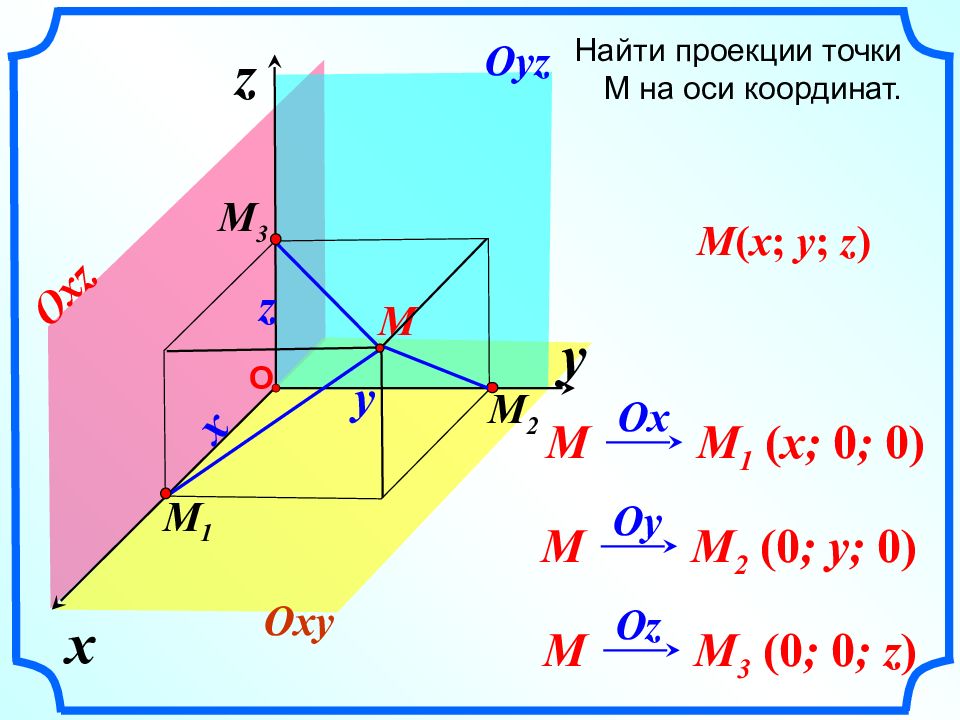
x z y О M x z Oxy Oyz Oxz M M 1 ( x; 0 ; 0) Ox M M 2 ( 0 ; y; 0 ) Oy M M 3 (0 ; 0 ; z ) Oz Найти проекции точки М на оси координат. M 2 M 1 M 3 y M ( x ; y ; z )
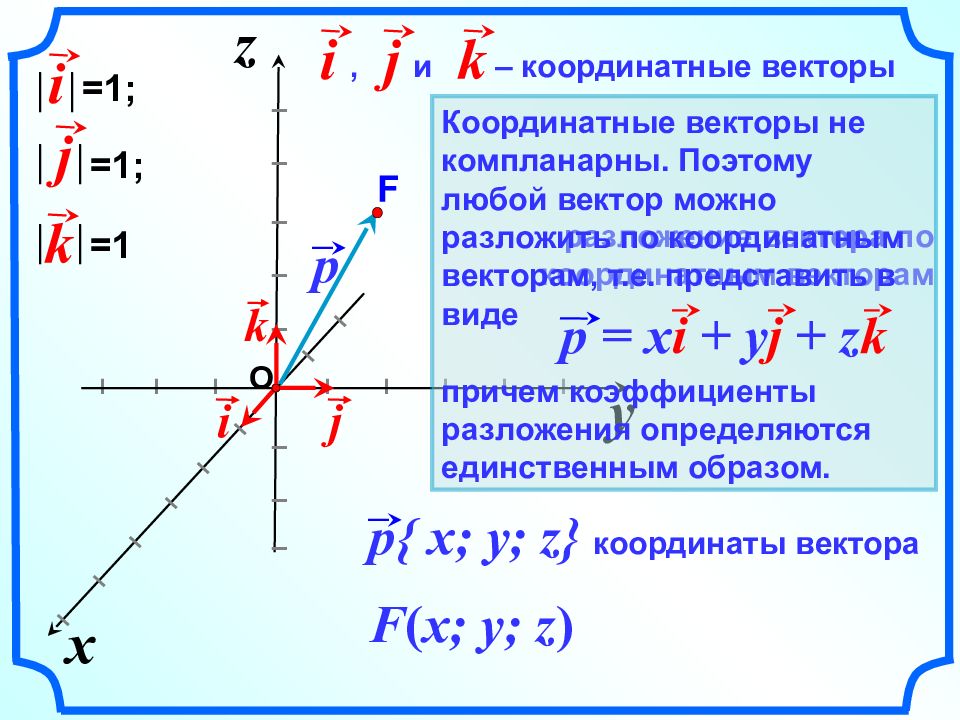
y x z I I I I I I I I I I I I I I I I I I I I I I I I j k i p{ x; y; z} координаты вектора разложение вектора по координатным векторам , и – координатные векторы i j k i =1; j =1; k =1 p F ( x; y; z ) O Координатные векторы не компланарны. Поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде причем коэффициенты разложения определяются единственным образом. p = x i + y j + z k F
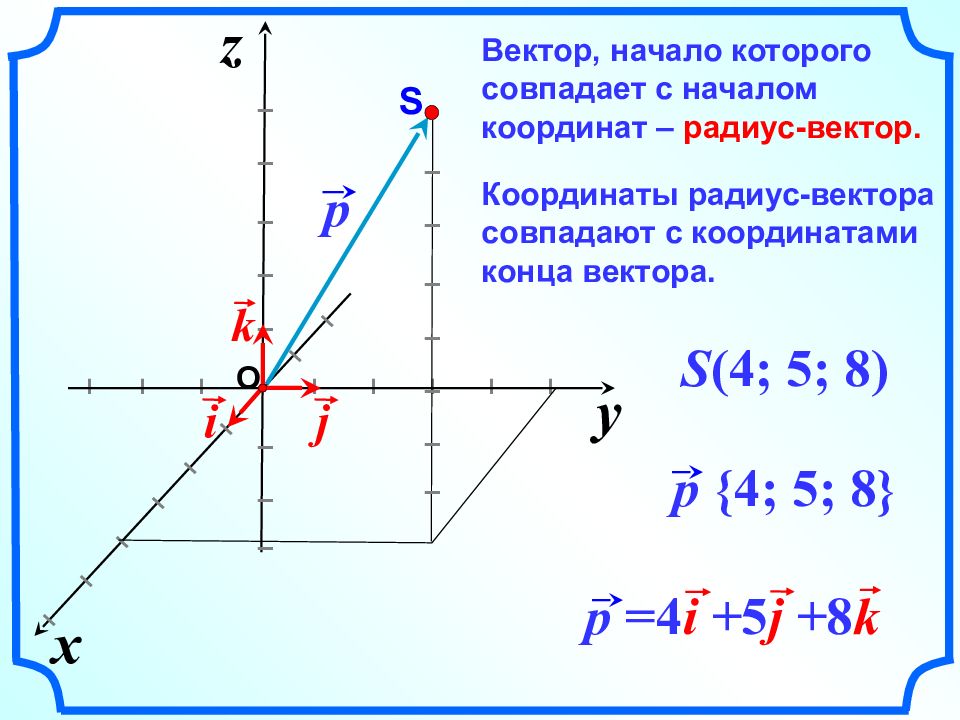
Вектор, начало которого совпадает с началом координат – радиус-вектор. Координаты радиус-вектора совпадают с координатами конца вектора. y x z I I I I I I I I I I I I I I I I I I I I I I I I j k i p {4; 5 ; 8 } S ( 4; 5 ; 8) p =4 i + 5 j + 8 k p I I I I I I I S O
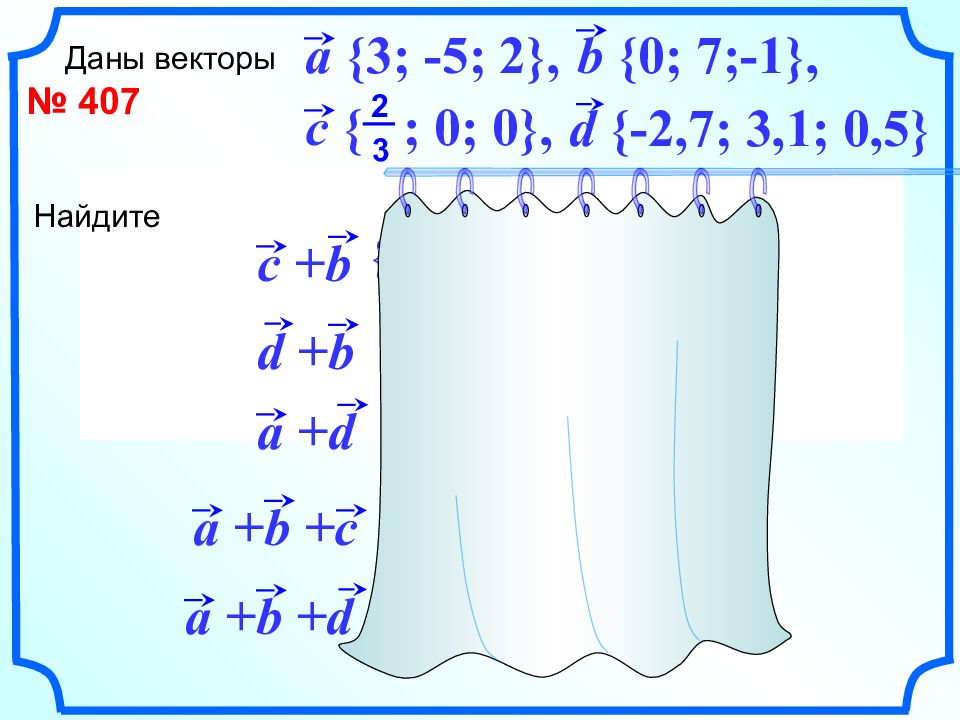
a {3;-5;2} b {0;7;-1} a +b {3;2;1} a {3;-5; 2} c { ;0; 0} 2 3 c +a { 3 ;-5;2} 2 3 + + № 407 Даны векторы d {-2,7; 3,1; 0,5} a {3; -5; 2}, b {0; 7;-1}, c { ; 0; 0}, 2 3 Найдите c +b d +b a +d a +b +c a +b +d {-2,7; 10,1; -0,5} {0,3; -1,9; 2,5} {3 ; 2; 1} 2 3 {0,3; 5,1; 1,5} { ;7;-1} 2 3
b {-8;12;-3} b {-8;12;-3} a {-6; 9;1} a {-6; 9;1} - a - b {2;-3; 4} + Найдите координаты вектора a - b -b {8;-12;3} (-1) 1 способ a - b {2;-3; 4} 2 способ a {-6; 9;1} b {-8;12;-3}
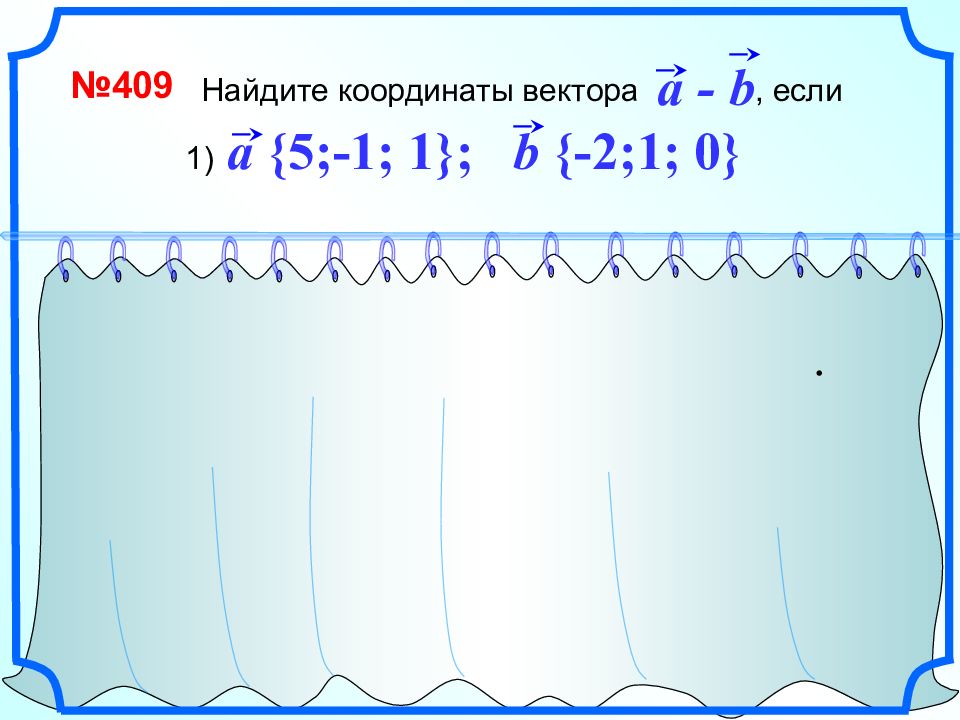
- + (-1) 1 способ a - b {7;-2; 1} 2 способ a {5;-1; 1} a {5;-1; 1} b {-2;1; 0} b {-2;1; 0} -b {2;-1; 0} a - b {7;-2; 1} Найдите координаты вектора, если a - b № 409 1) a {5;-1; 1}; b {-2;1; 0}
