Координаты вектора Л.С. Атанасян "Геометрия 7-9"
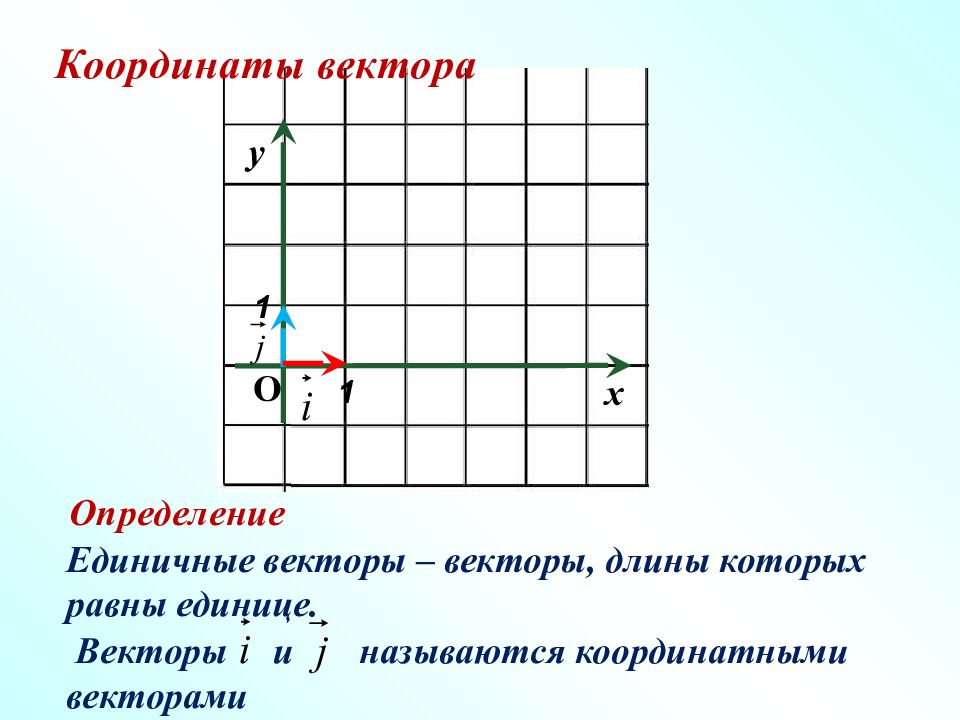
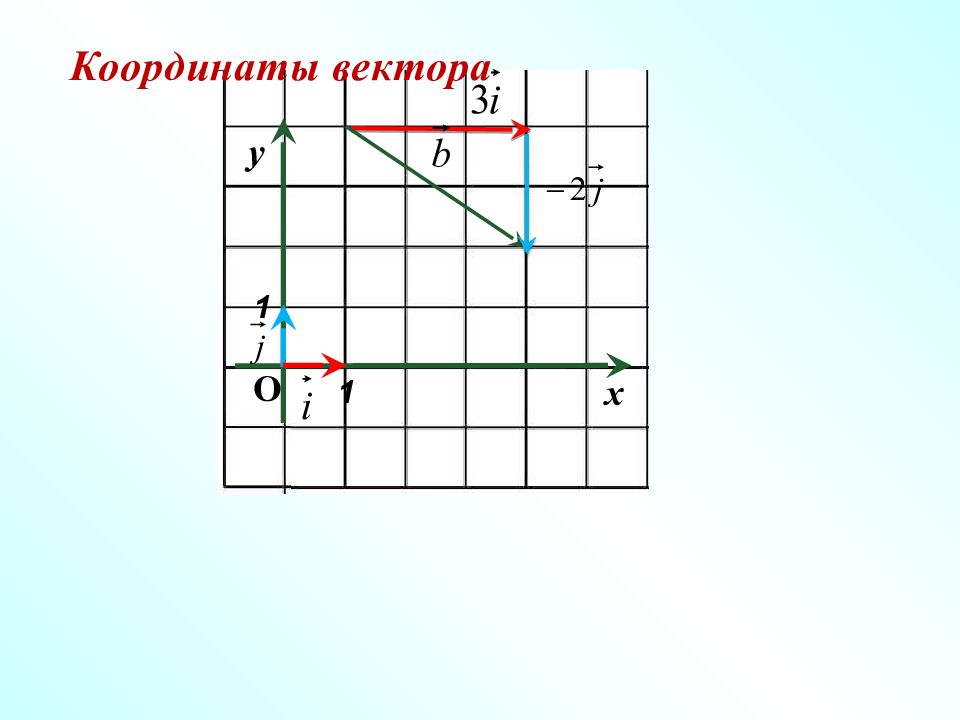
1 х 1 у О Координаты вектора Определение Единичные векторы – векторы, длины которых равны единице. Векторы и называются координатными векторами
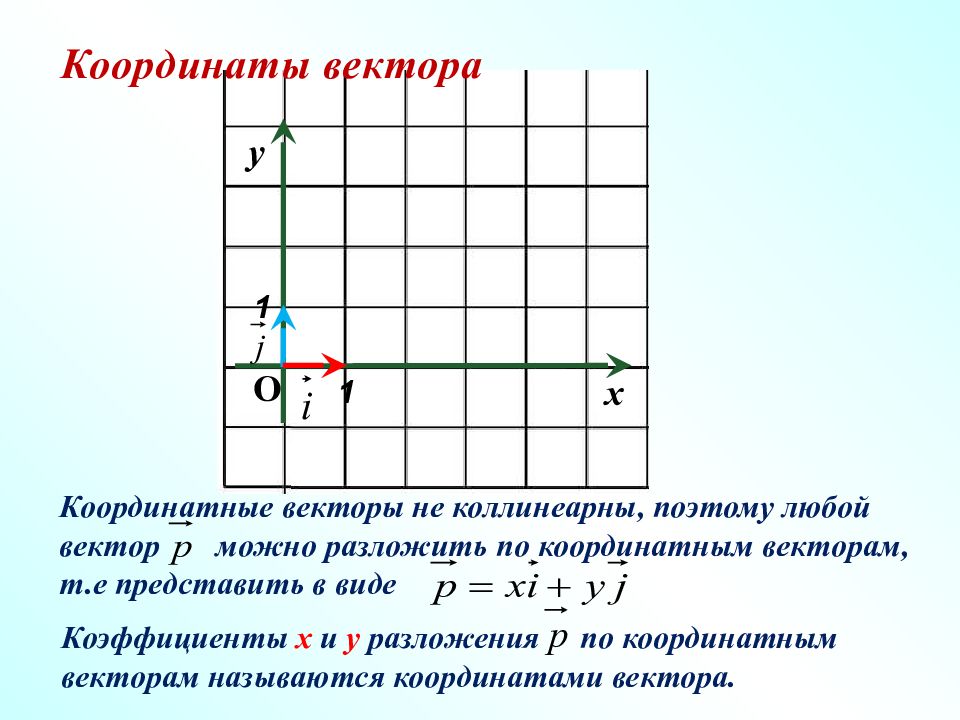
1 х 1 у О Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т.е представить в виде Коэффициенты x и y разложения по координатным векторам называются координатами вектора. Координаты вектора
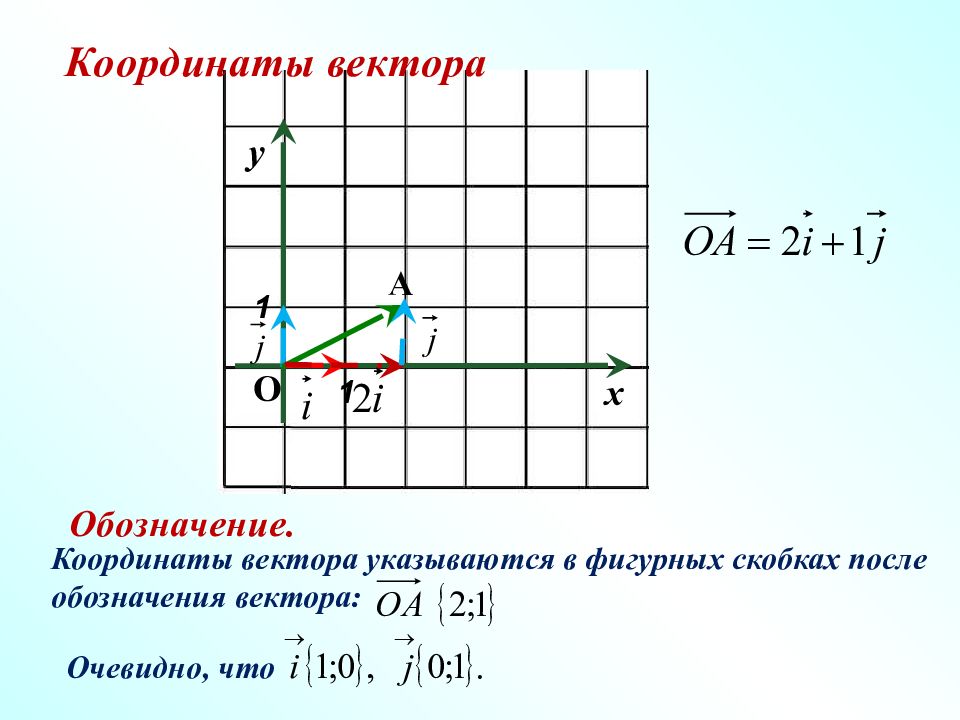
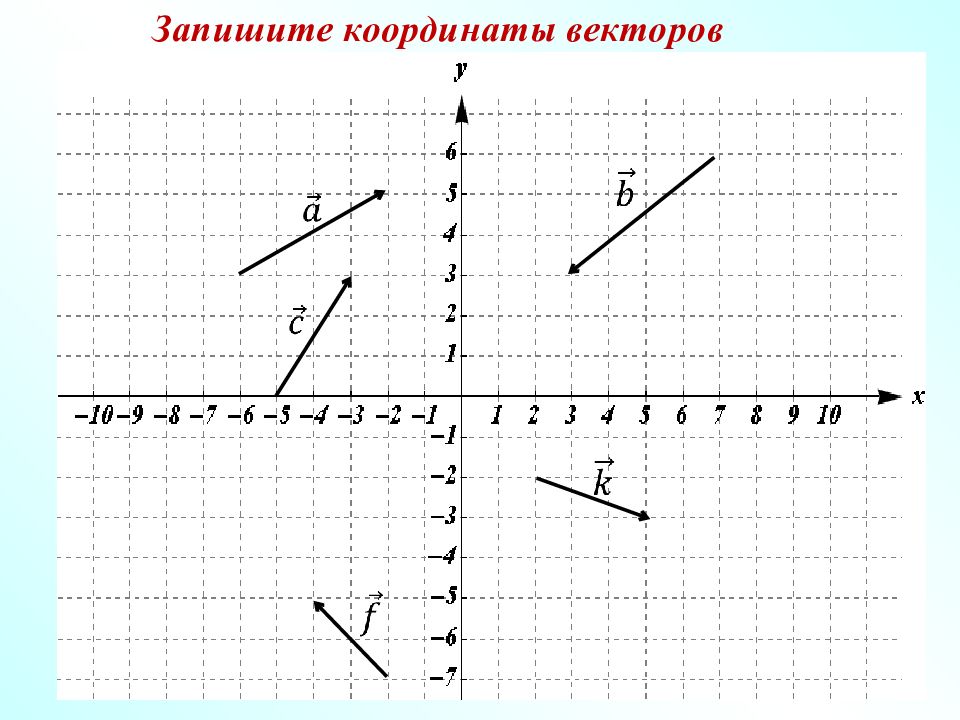
1 х 1 у О A Обозначение. Координаты вектора Координаты вектора указываются в фигурных скобках после обозначения вектора: Очевидно, что
О p и координатные векторы i j p{ x; y} координаты вектора p {4; 3} F i =1; j =1 p = x i + y j разложение вектора по координатным векторам F ( 4; 3 ) j p =4 i + 3 j Вектор, начало которого совпадает с началом координат – радиус-вектор. Координаты радиус-вектора совпадают с координатами конца вектора. x y B A 1 i i i i j j
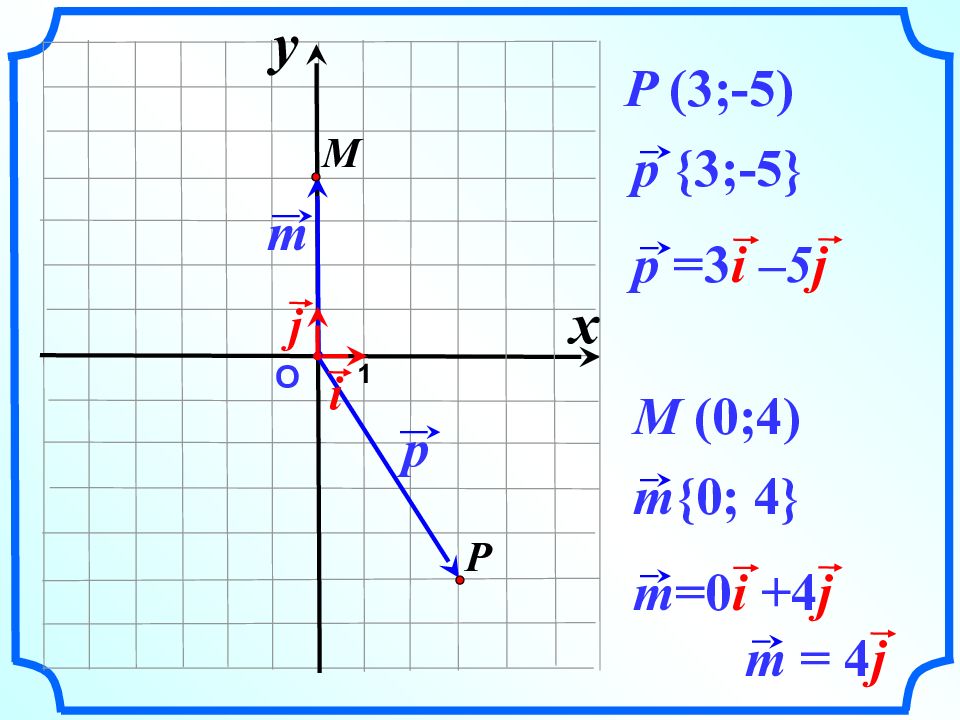
О p p {3;-5} P 1 P ( 3;-5 ) i p =3 i –5 j m j M m {0; 4} M ( 0;4 ) m =0 i + 4 j x y m = 4 j
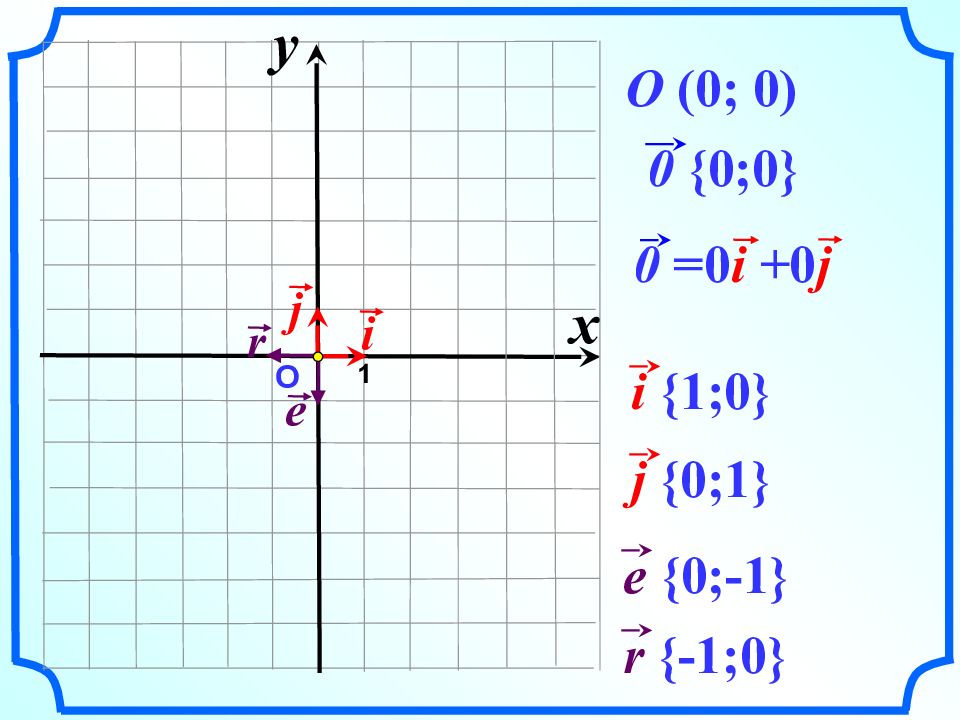
О 0 {0;0} 1 O ( 0; 0 ) i 0 =0 i + 0 j j x y i {1;0} j {0;1} e r e {0;-1} r {-1;0}
1 х 1 у О Координаты вектора
Запишите координаты векторов
№921 (а, б) Свойства координатных векторов
3. Каждая координата суммы двух векторов или более векторов равна сумме соответствующих координат этих векторов. Свойства координатных векторов №922(а, б)
Свойства координатных векторов 4. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. №923 (а, б)
5. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число. Свойства координатных векторов №924 (а, б)
Координаты вектора
Домашнее задание п.89, 90. Записать в тетрадь свойства координатных векторов (слайд 10 – 13 презентации). Выполнить задание на Якласс. Срок выполнения до 18 октября (8:00).
Проверим координаты векторов
