ОГЭ. Задание № 19 Подготовила учитель математики МОУ Школа с.Харсаим Филиппова Р.Р.
Задание 19 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по сути выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи.
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник
За единицу измерения площадей принимают квадрат со стороной 1см. Квадратный метр, производная единица Международной системы единиц (СИ) ; 1 м² = 1 са ( сантиар ); Квадратный километр, 1 км² = 1 000 000 м²; Гектар, 1 га = 10 000 м²; Ар (сотка), 1 а = 100 м²: Квадратный дециметр, 100 дм² = 1 м²; Квадратный сантиметр, 10 000 см² = 1 м²; Квадратный миллиметр, 1 000 000 мм² = 1 м²;
Фигуры имеющие равные площади называются равновеликими. Равные многоугольники имеют равные площади. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Площадь квадрата равна квадрату его стороны.
Площади треугольников S = ½* a*h S = ½* a*b sinα S = r*p S = S = - формула Герона ( p = - полупериметр) S = π * R 2 площадь круга
Площади четырехугольников Прямоугольник S=a*b S= ½* d 2 sinφ а и в – стороны прямоугольника d - диагональ прямоугольника φ- угол между диагоналями Квадрат S = a 2 S =1/2* d 2 а – сторона квадрата d - диагональ квадрата Параллелограмм S=a*h S=a*b* sinα S= ½* d 1 *d 2 sinφ Ромб S=a*h S=a 2 sinα S= ½* d 1 *d 2 Трапеция S = S = ½* d 1 * d 2 sinφ а и в – основания трапеции; -длина средней линии ; d 1 и d 2 -диагонали трапеции; sinφ -угол между диагоналями
Одним из основных заданий Модуля Геометрия являются задачи на нахождение площади фигур на сетке. Многие ученики сводят решение этого задания к подсчету клеток внутри фигуры. Такой способ не всегда дает точный результат. Поэтому я предлагаю рассмотреть основные способы решения таких задач.
Способ №1 ИСПОЛЬЗОВАНИЕ ФОРМУЛ 1. Используя рисунок определим длину катетов. 2. Вычислим площадь прямоугольного треугольника по формуле S= 1/2 a*b. а=4 b =3 S= 1/2* 4*3= 6
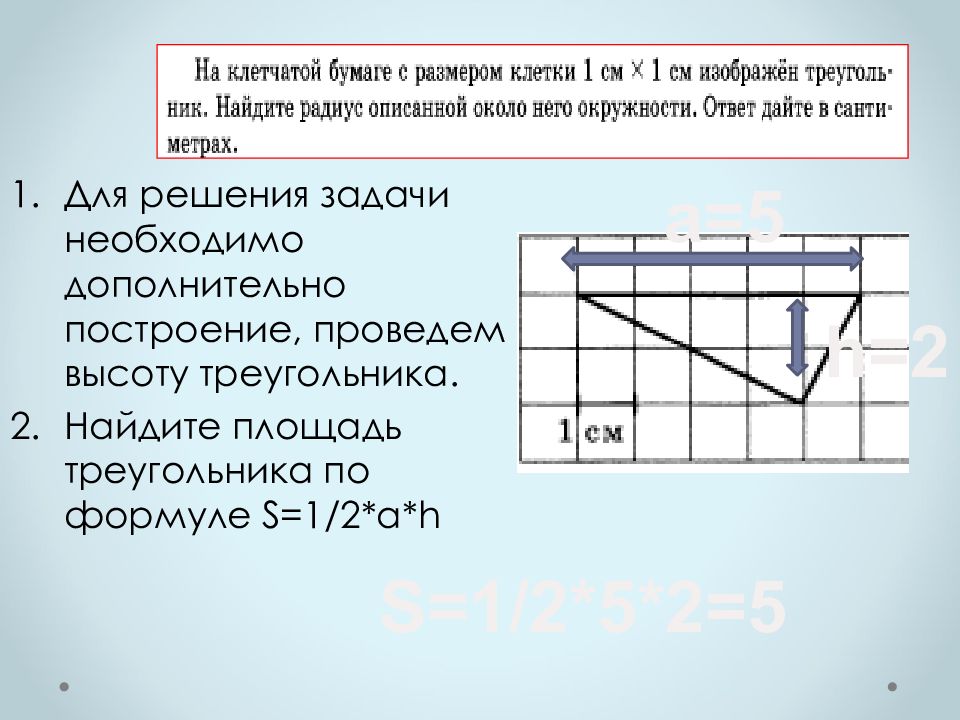
Для решения задачи необходимо дополнительно построение, проведем высоту треугольника. Найдите площадь треугольника по формуле S=1 /2*а* h а=5 h =2 S=1 /2*5*2=5
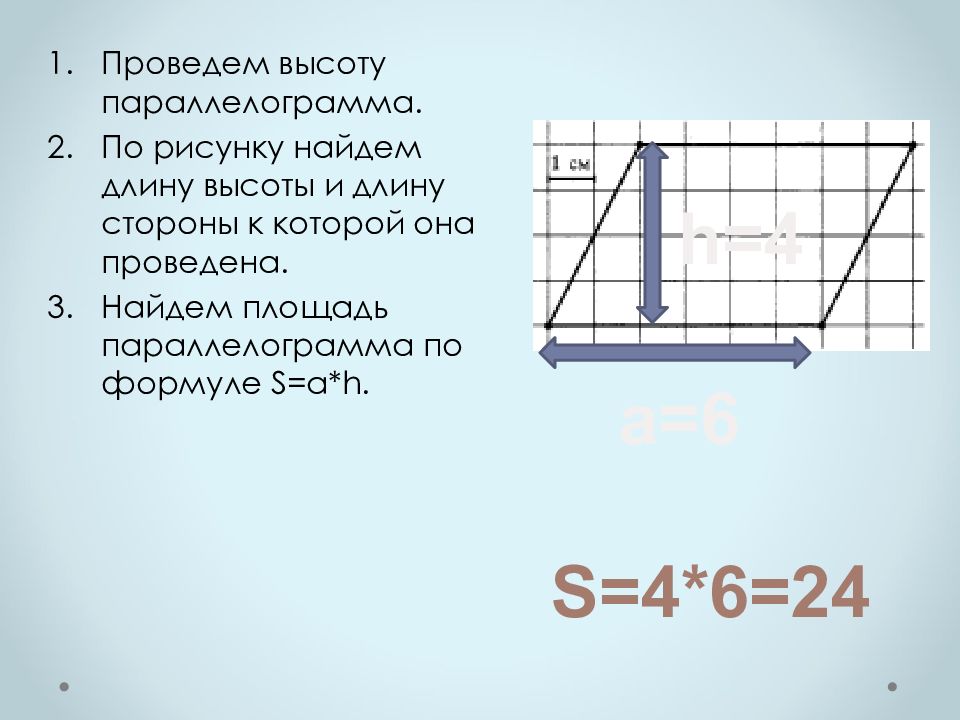
Проведем высоту параллелограмма. По рисунку найдем длину высоты и длину стороны к которой она проведена. Найдем площадь параллелограмма по формуле S=a*h. h=4 a=6 S=4*6=24
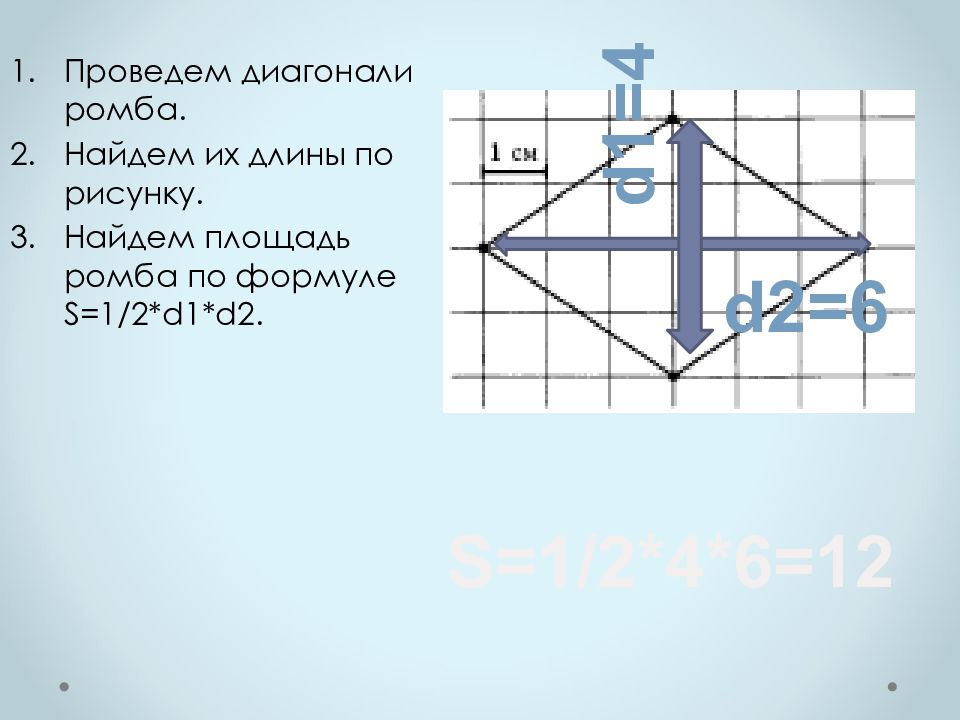
Проведем диагонали ромба. Найдем их длины по рисунку. Найдем площадь ромба по формуле S=1 /2 *d1*d2. d1=4 d2=6 S=1 / 2*4*6=12
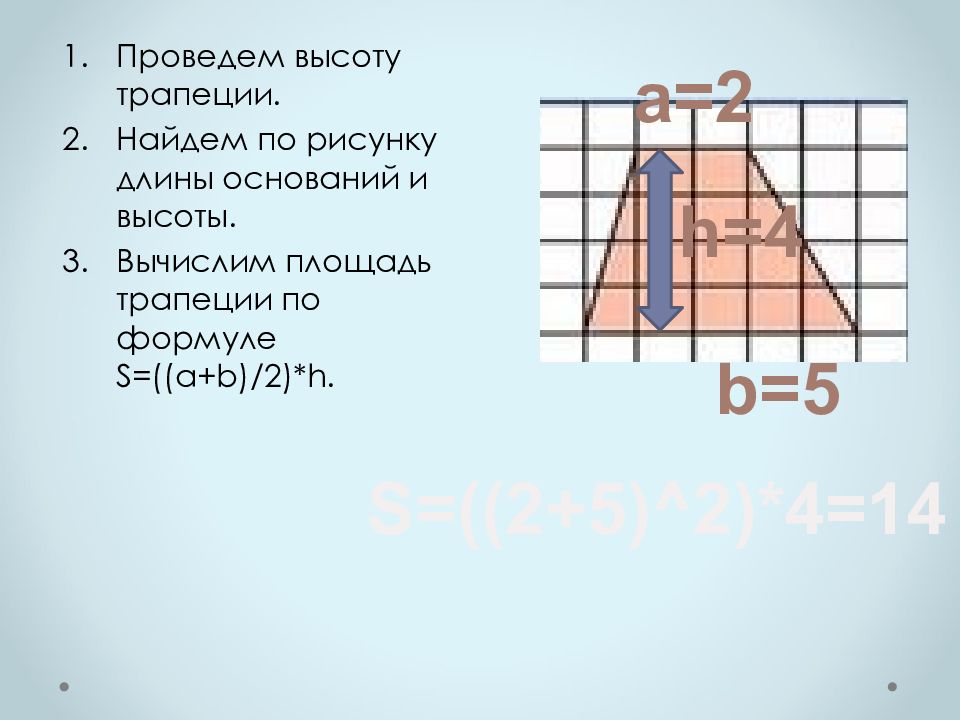
Проведем высоту трапеции. Найдем по рисунку длины оснований и высоты. Вычислим площадь трапеции по формуле S= ( (a+b) /2)* h. а=2 h=4 b=5 S=((2+5)^2)*4=14
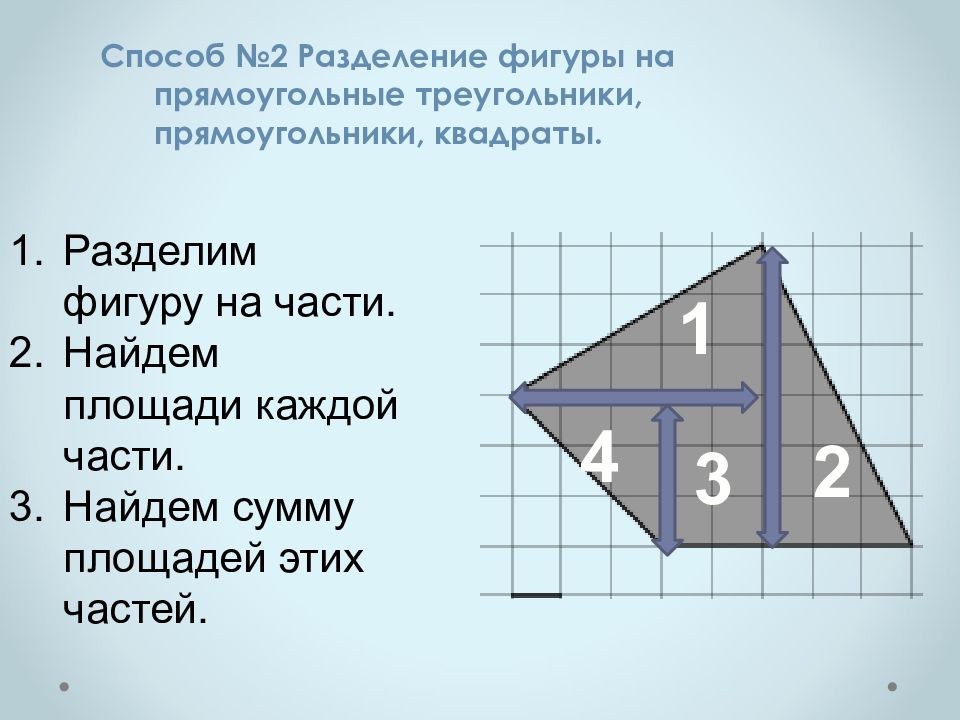
Способ №2 Разделение фигуры на прямоугольные треугольники, прямоугольники, квадраты. Разделим фигуру на части. Найдем площади каждой части. Найдем сумму площадей этих частей. 2 3 4 1
Фигуры 1,4,2 –прямоугольные треугольники. Их площади найдем по формуле S=1 /2* a*b. Фигура 3-прямоугольник. Его площадь легко найти даже подсчетам клеток. Его площадь равна 6. Сложив площади треугольников и прямоугольника мы найдем площадь искомой фигуры.
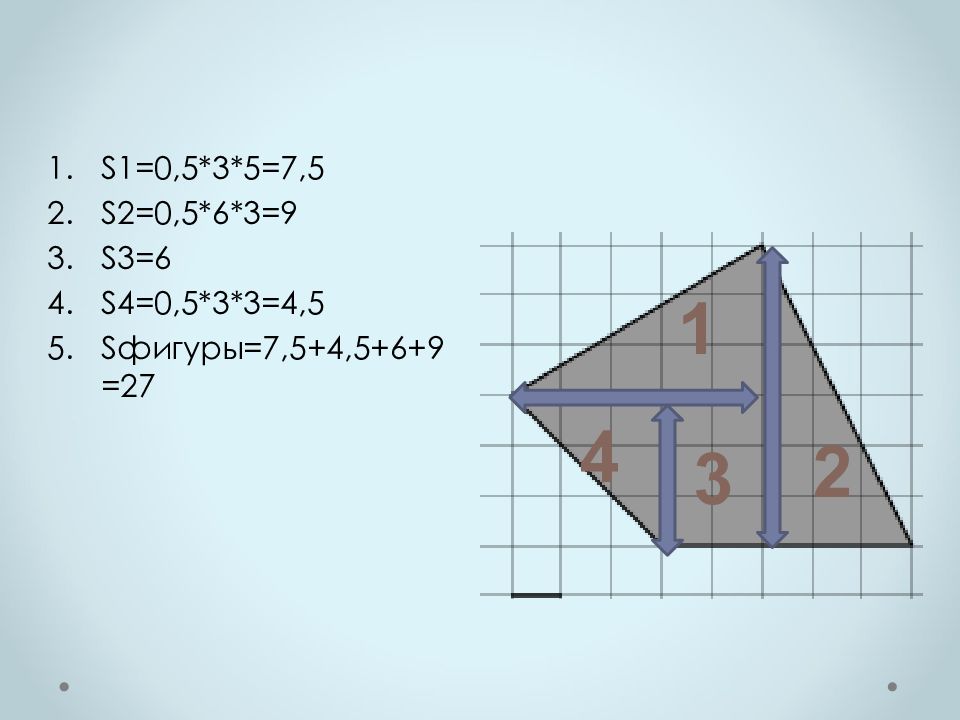
2 3 4 1 S1=0,5*3*5=7,5 S2 =0,5*6*3=9 S3=6 S4 =0,5*3*3=4,5 S фигуры=7,5+4,5+6+9=27
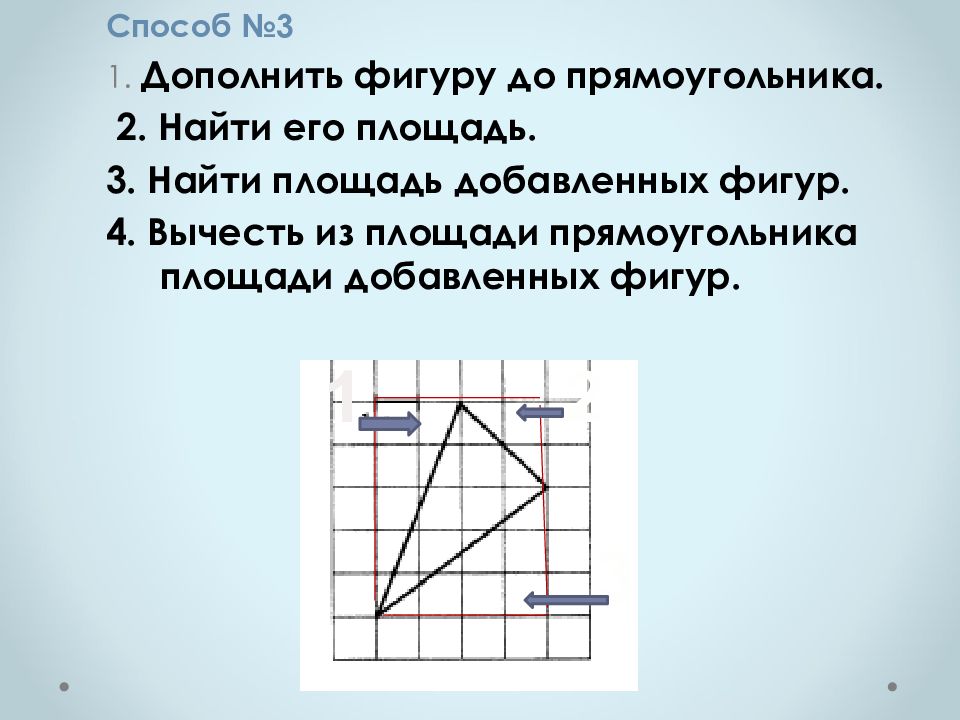
Способ №3 1. Дополнить фигуру до прямоугольника. 2. Найти его площадь. 3. Найти площадь добавленных фигур. 4. Вычесть из площади прямоугольника площади добавленных фигур. 1 2 3
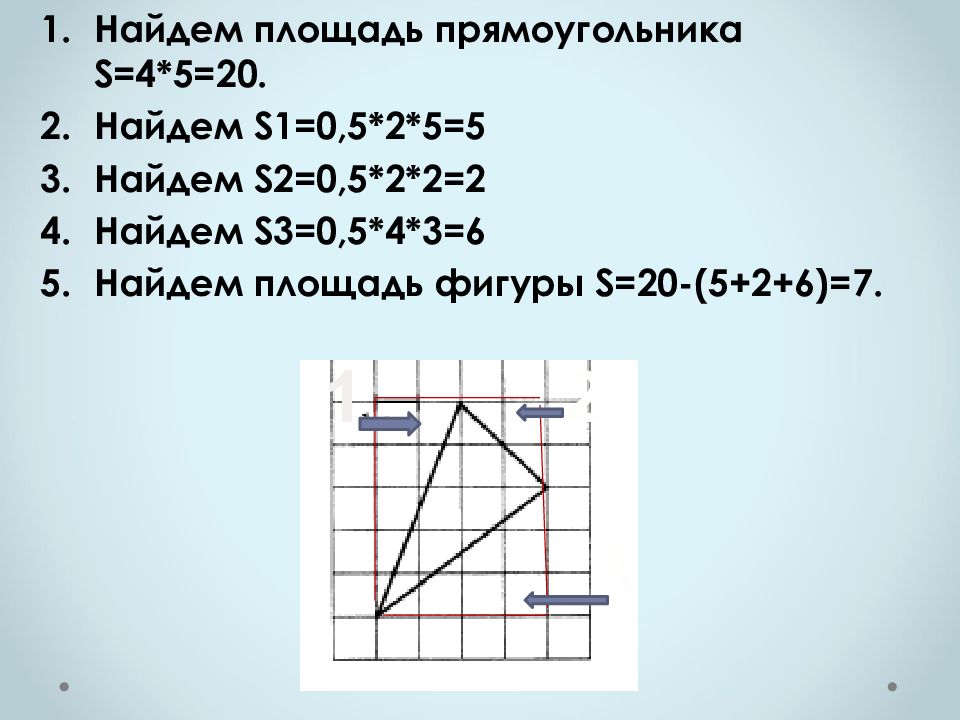
Найдем площадь прямоугольника S =4*5=20. Найдем S1 =0,5*2*5=5 Найдем S2 =0,5*2*2=2 Найдем S3=0,5*4*3=6 Найдем площадь фигуры S=20-(5+2+6)=7. 1 2 3
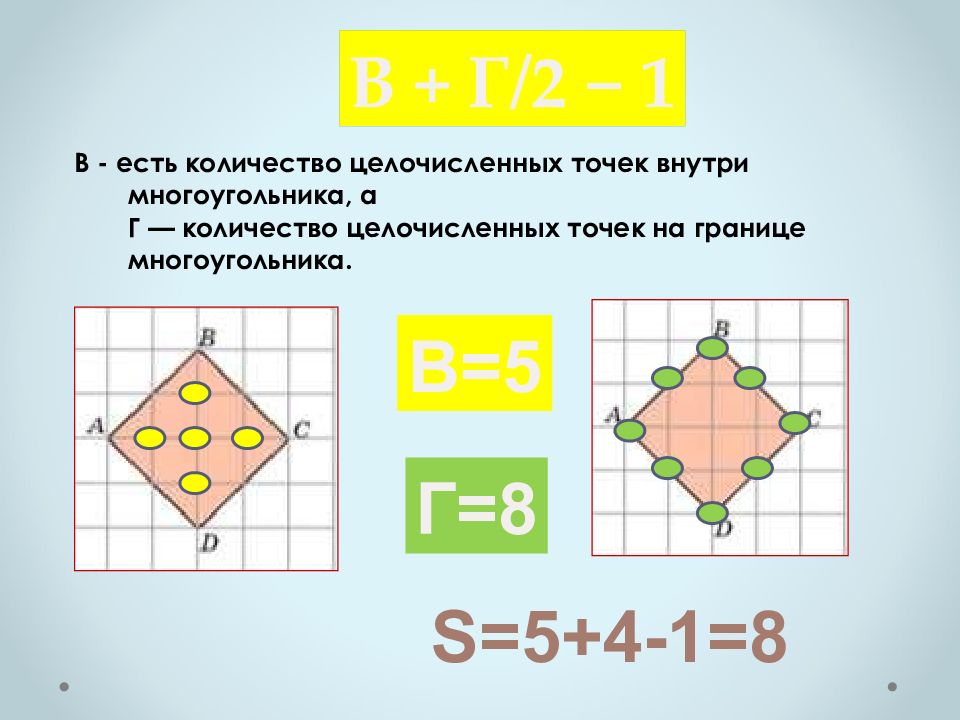
Способ №4 Формула Пика. Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1, где В - есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
В - есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника. В + Г/2 − 1 В=5 Г=8 S=5+4-1=8
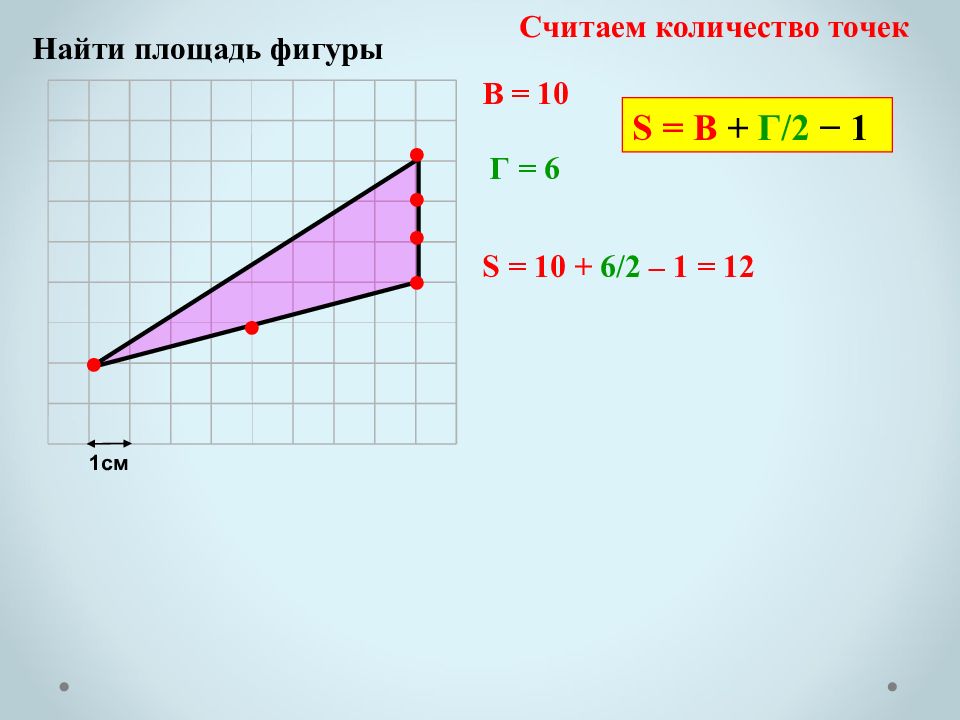
1см Найти площадь фигуры В = 1 0 Г = 6 S = 1 0 + 6/2 – 1 = 12 ● ● ● ● ● ● Считаем количество точек S = В + Г/2 − 1
1 2
3 4
5 6
