Первый слайд презентации: Сечения куба, призмы, пирамиды
Подготовил: преподаватель ГАПОУ ТО «ТКПСТ» Хазова Е.С. Государственное автономное профессиональное учреждение Тюменской области «Тюменский колледж производственных и социальных технологий»
Слайд 2: Сечение многогранников
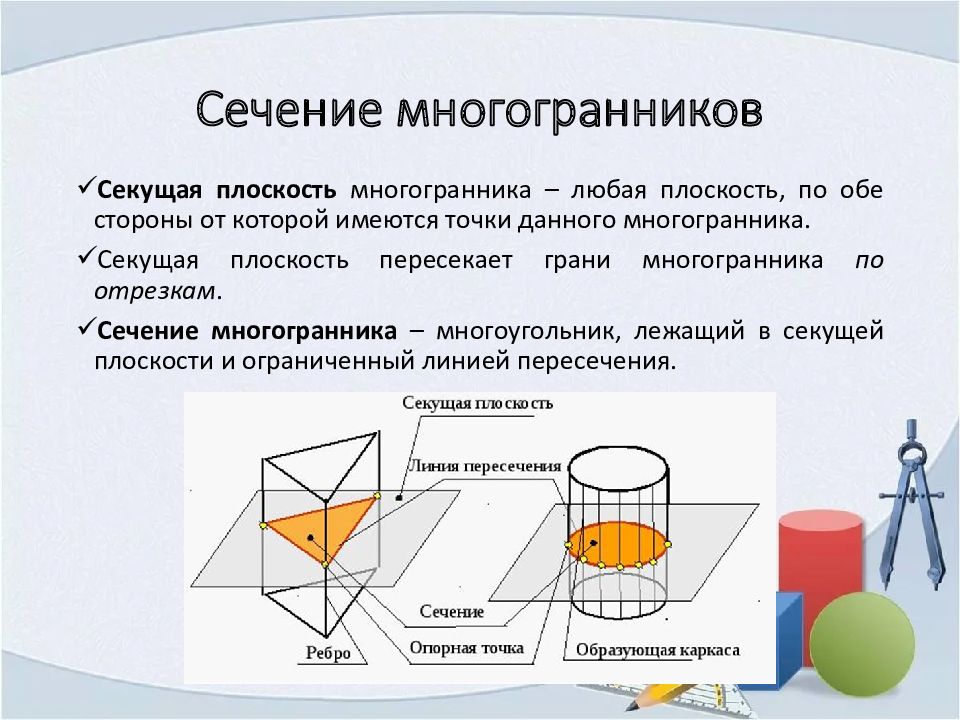
Секущая плоскость многогранника – любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Сечение многогранника – многоугольник, лежащий в секущей плоскости и ограниченный линией пересечения.
Слайд 3: Сечение тетраэдра
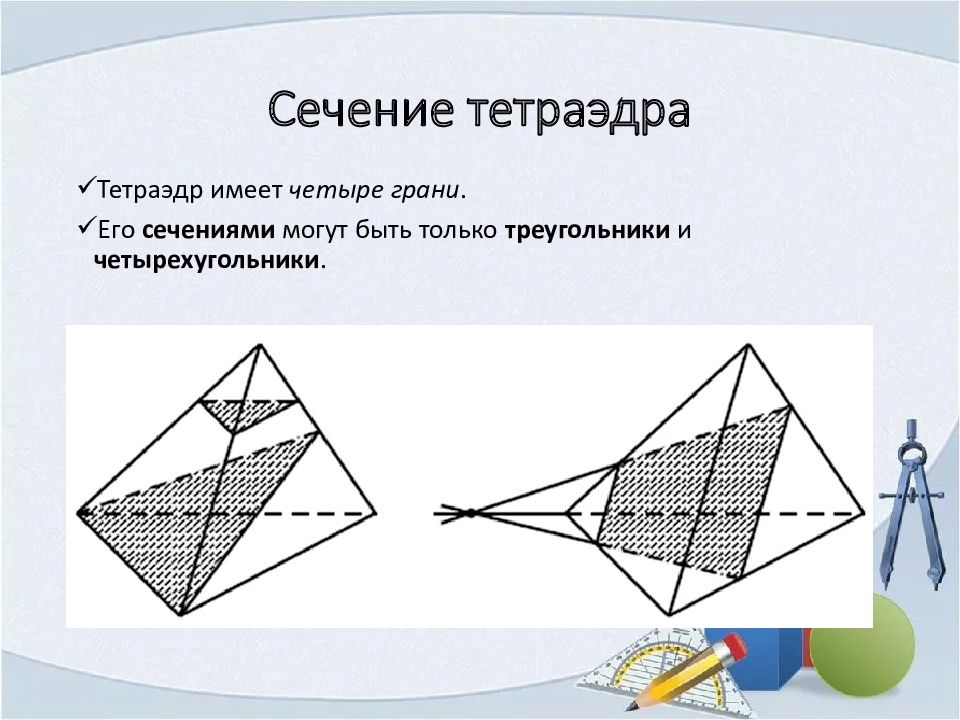
Тетраэдр имеет четыре грани. Его сечениями могут быть только треугольники и четырехугольники.
Слайд 4: Сечение параллелепипеда
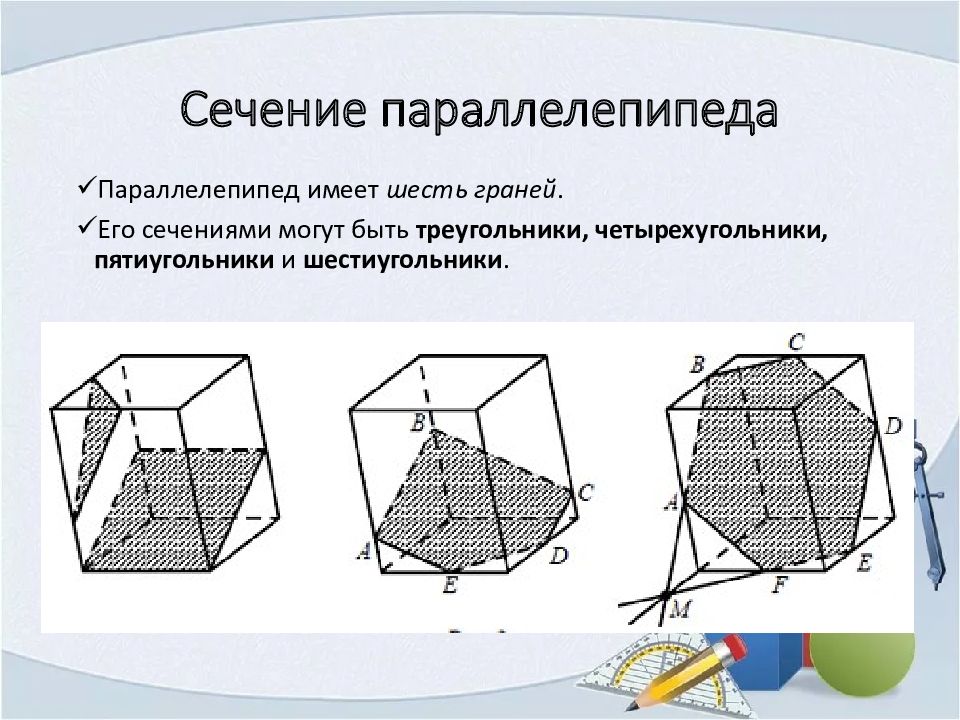
Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.
Слайд 5: Теоремы, используемые при построении сечений
Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.
Слайд 6: Теоремы, используемые при построении сечений
Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Слайд 7: Теоремы, используемые при построении сечений
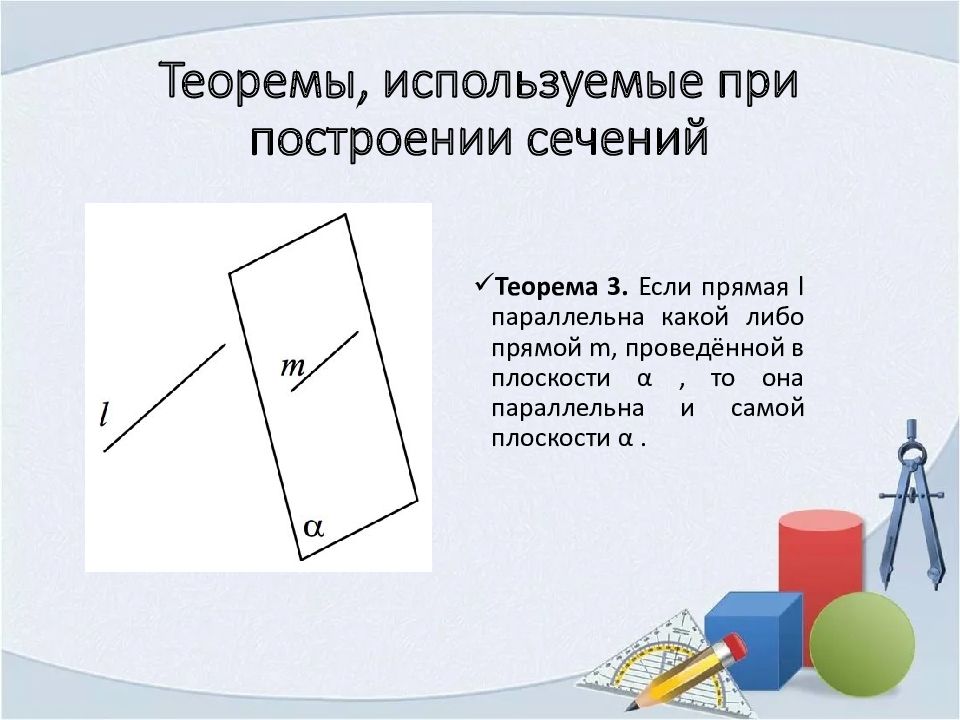
Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости α, то она параллельна и самой плоскости α.
Слайд 8: Теоремы, используемые при построении сечений
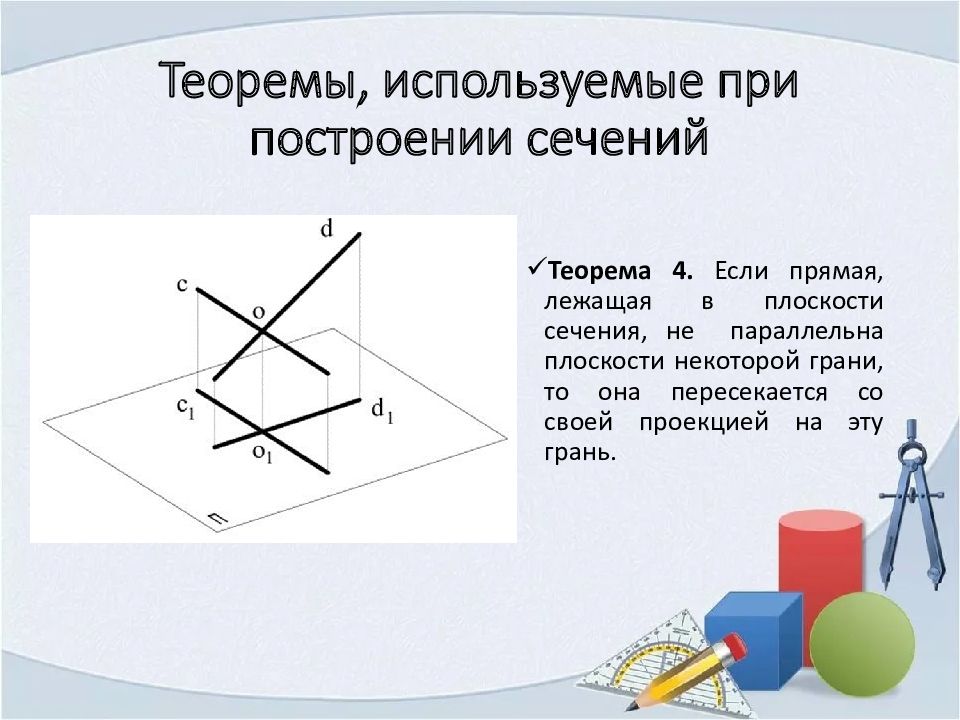
Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.
Слайд 9: Алгоритм построения сечения
Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани – сторона сечения. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки – новые точки секущей плоскости, лежащие в плоскостях граней. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.
Слайд 10: Контроль правильности построенного сечения
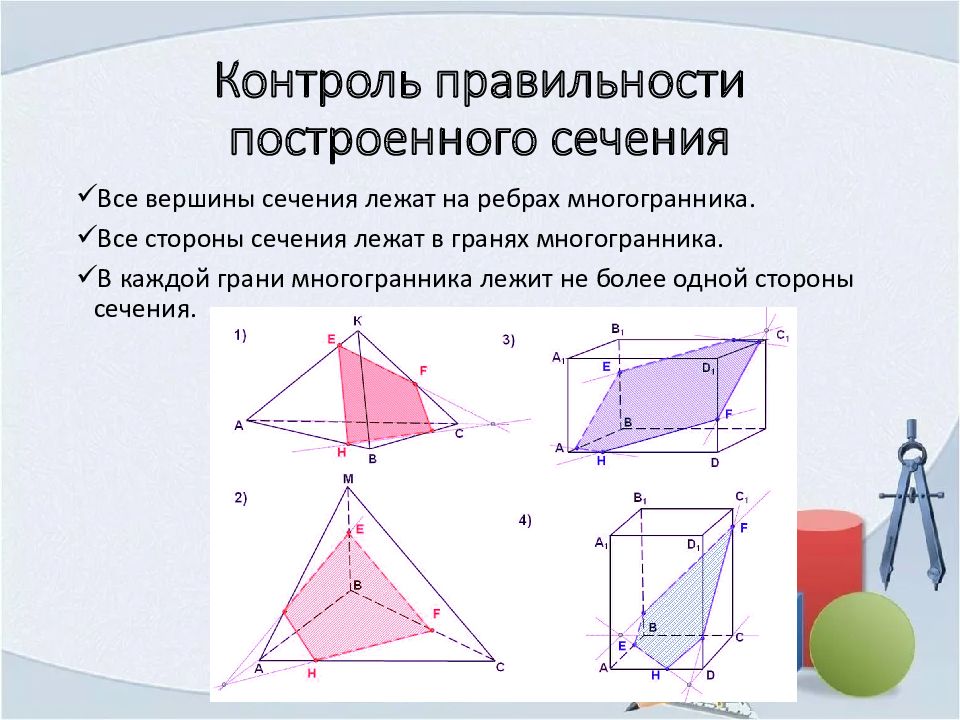
Все вершины сечения лежат на ребрах многогранника. Все стороны сечения лежат в гранях многогранника. В каждой грани многогранника лежит не более одной стороны сечения.
Слайд 11: Пример 1
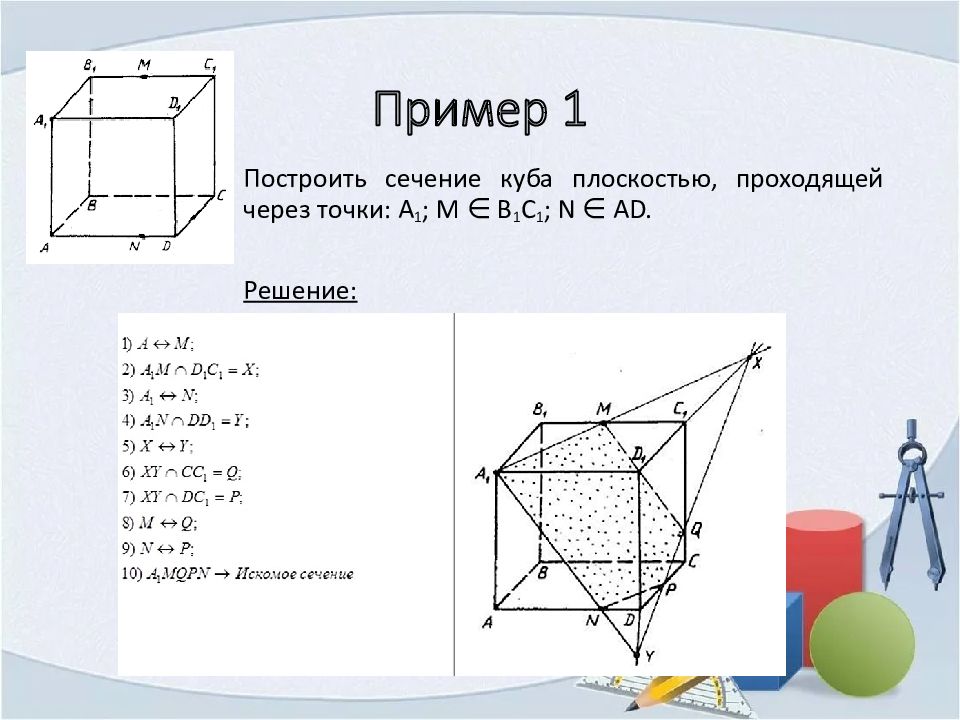
Построить сечение куба плоскостью, проходящей через точки: A 1 ; M ∈ B 1 C 1 ; N ∈ AD. Решение:
Слайд 12: Пример 2
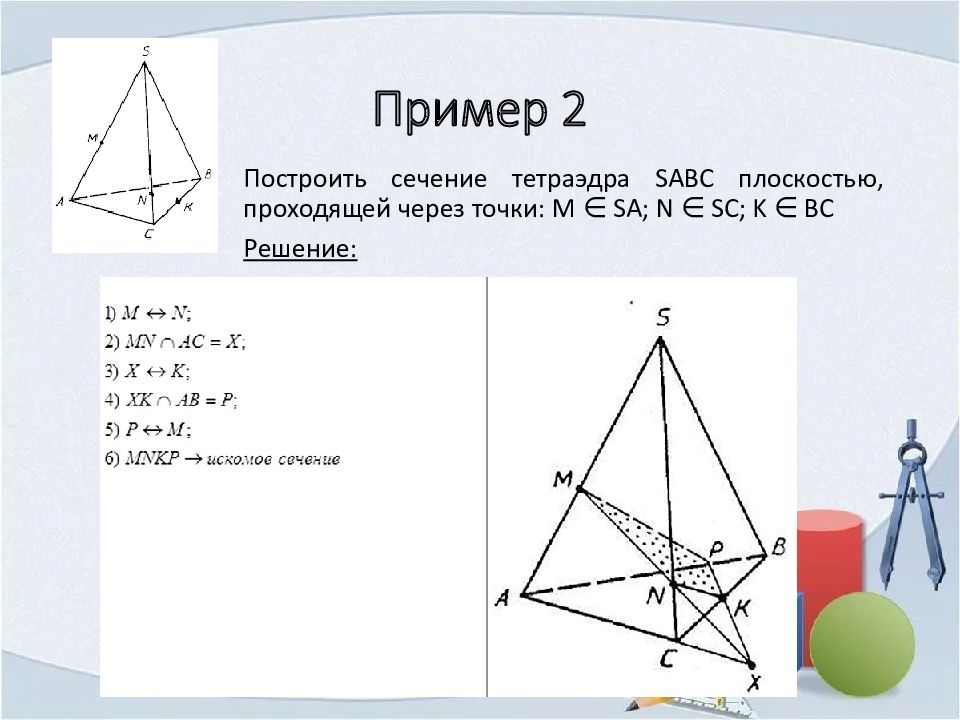
Построить сечение тетраэдра SABC плоскостью, проходящей через точки: M ∈ SA; N ∈ SC; K ∈ BC Решение:
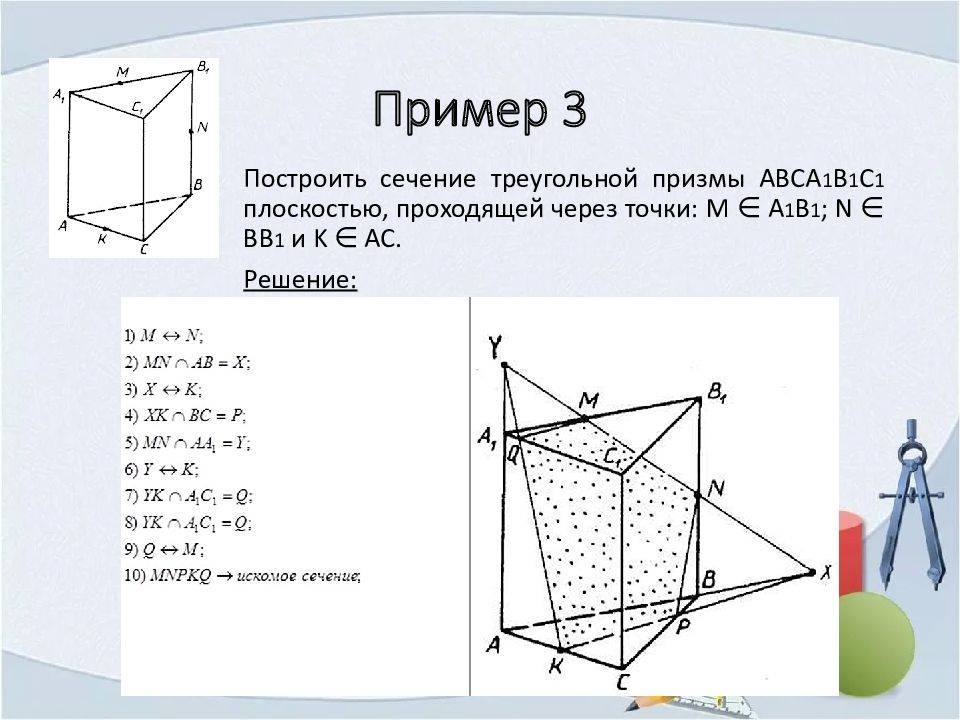
Слайд 13: Пример 3
Построить сечение треугольной призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки: M ∈ A 1 B 1 ; N ∈ BB 1 и K ∈ AC. Решение:
Последний слайд презентации: Сечения куба, призмы, пирамиды: Задания для самостоятельного решения
Построить сечение куба плоскостью, проходящей через точки: M ∈ C 1 D 1 ; B 1 и N ∈ AD. Построить сечение треугольной призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки: M ∈ AC; N ∈ CC 1 ; K ∈ BB 1. Построить сечение куба плоскостью, проходящей через точки: M ∈ грани A 1 B 1 C 1 D 1 ; N ∈ DD 1 и K ∈ AD.