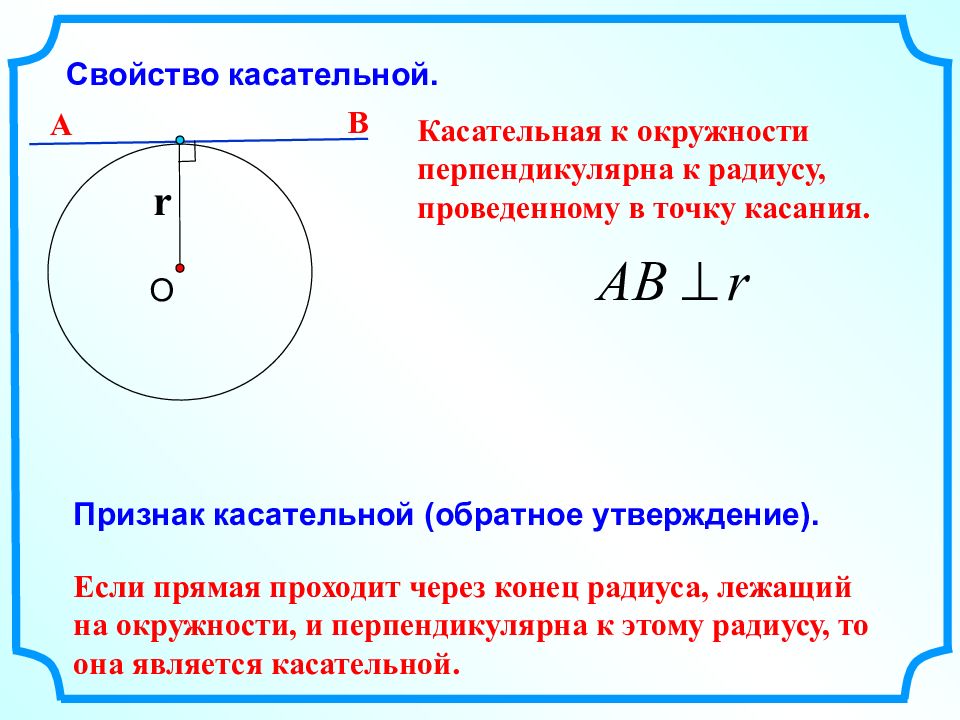
Свойство касательной. О r Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. А В Признак касательной (обратное утверждение). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
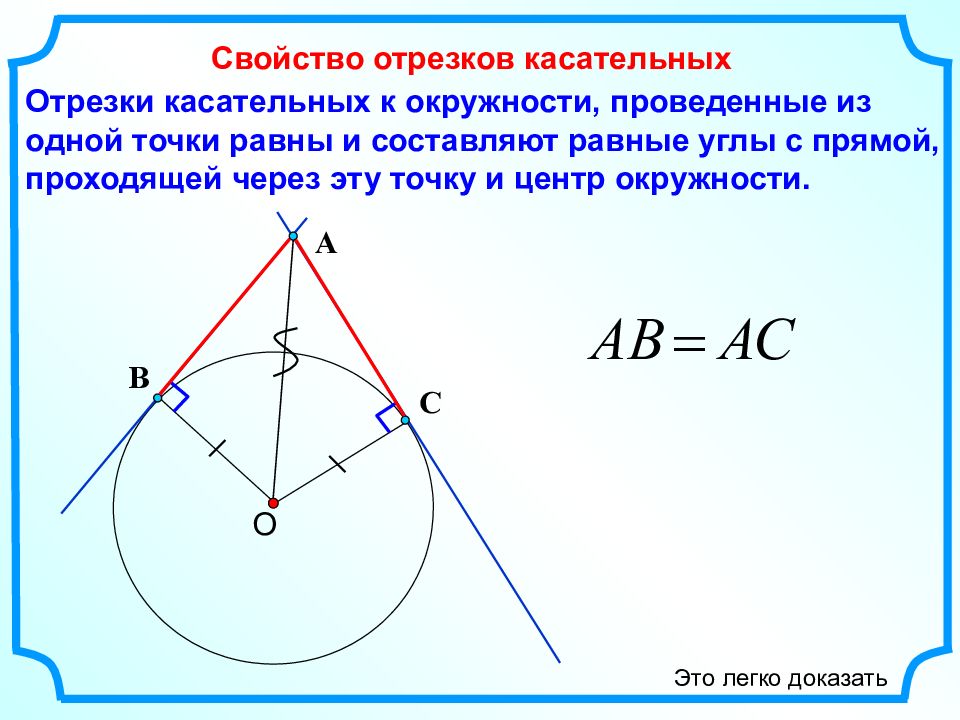
Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Свойство отрезков касательных О С А В Это легко доказать
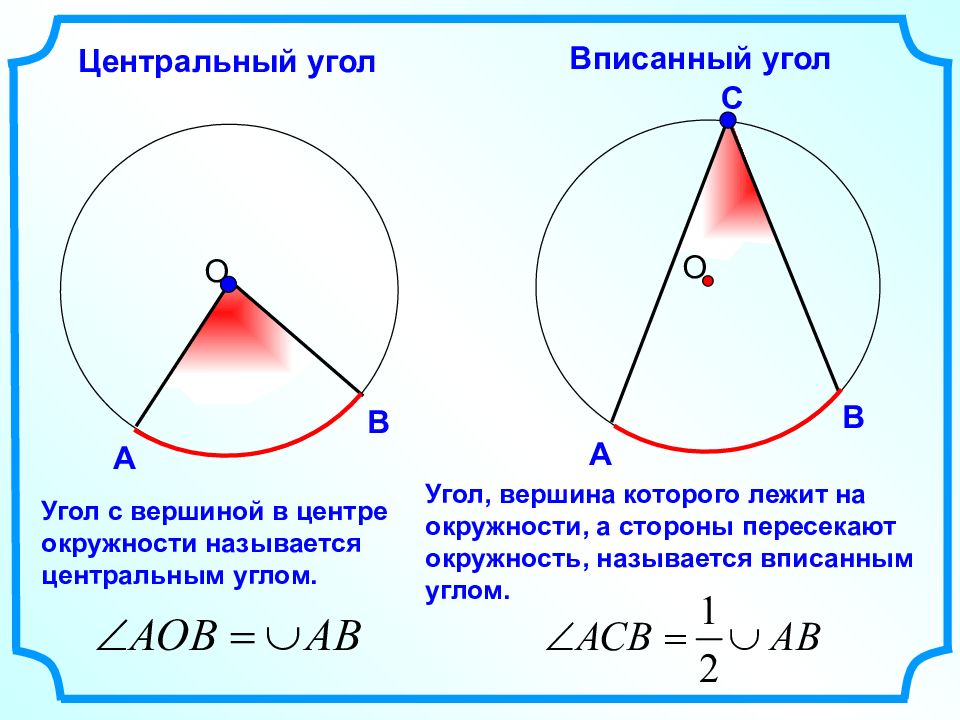
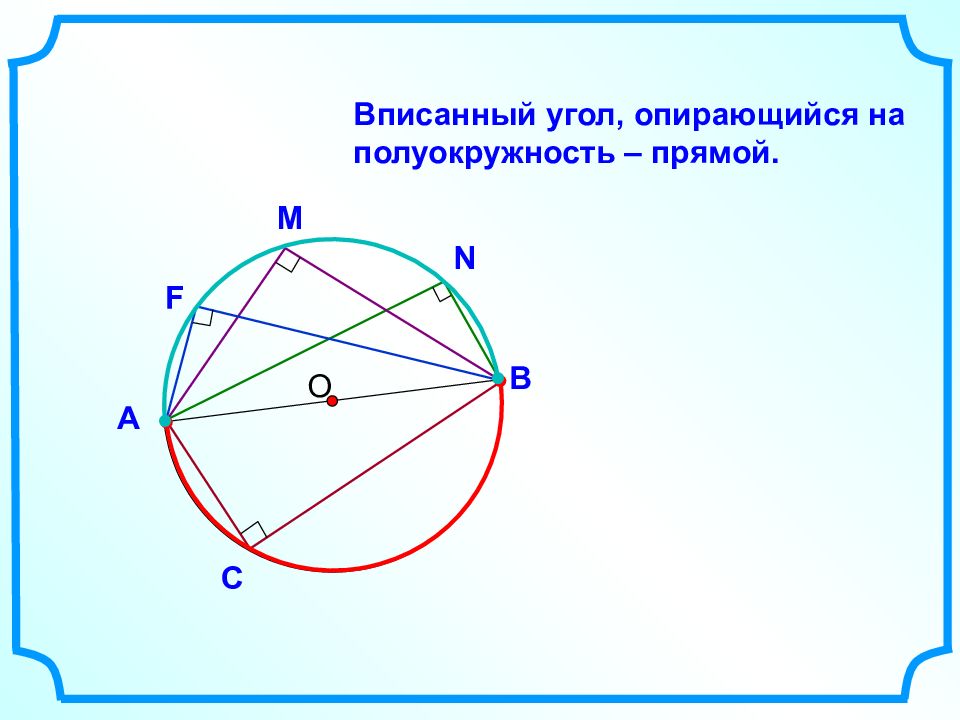
А В С А В О О Центральный угол Вписанный угол Угол с вершиной в центре окружности называется центральным углом. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
О Вписанные углы, опирающиеся на одну и ту же дугу, равны. В N M А С F
О Вписанный угол, опирающийся на полуокружность – прямой. В N M А С F
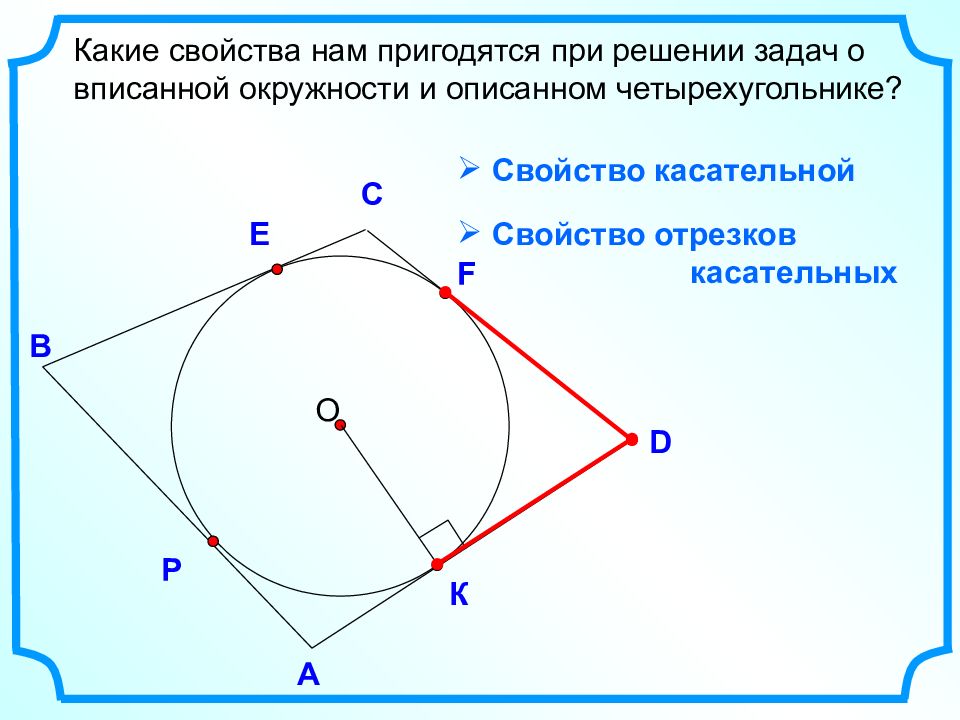
D В С Какие свойства нам пригодятся при решении задач о вписанной окружности и описанном четырехугольнике? А E О К Свойство касательной Свойство отрезков касательных F P
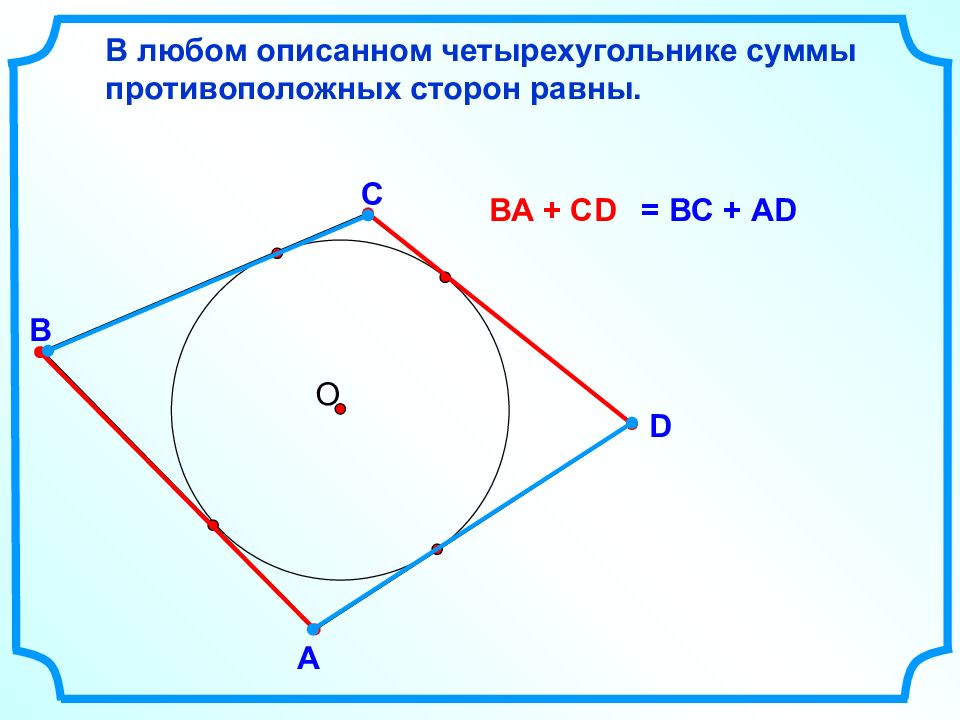
D В С В любом описанном четырехугольнике суммы противоположных сторон равны. А О = ВС + AD ВА + CD
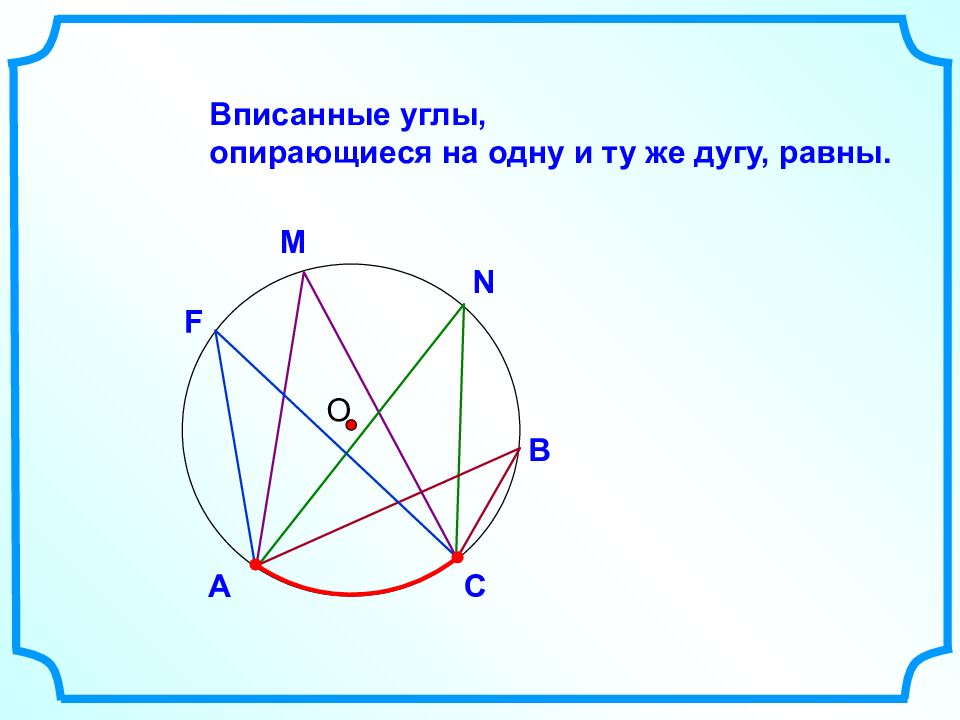
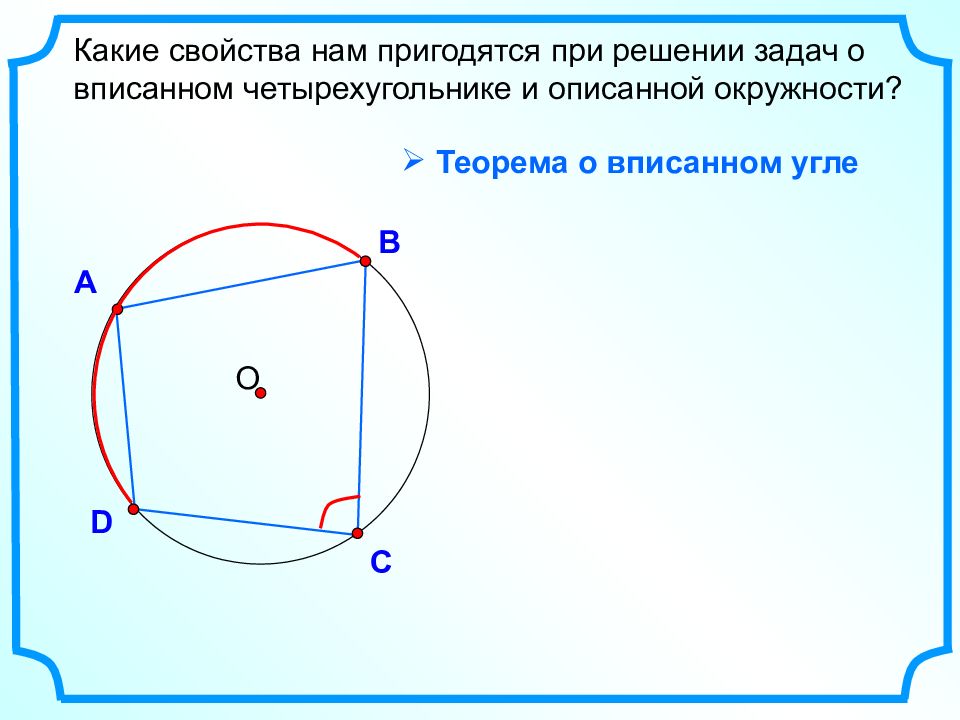
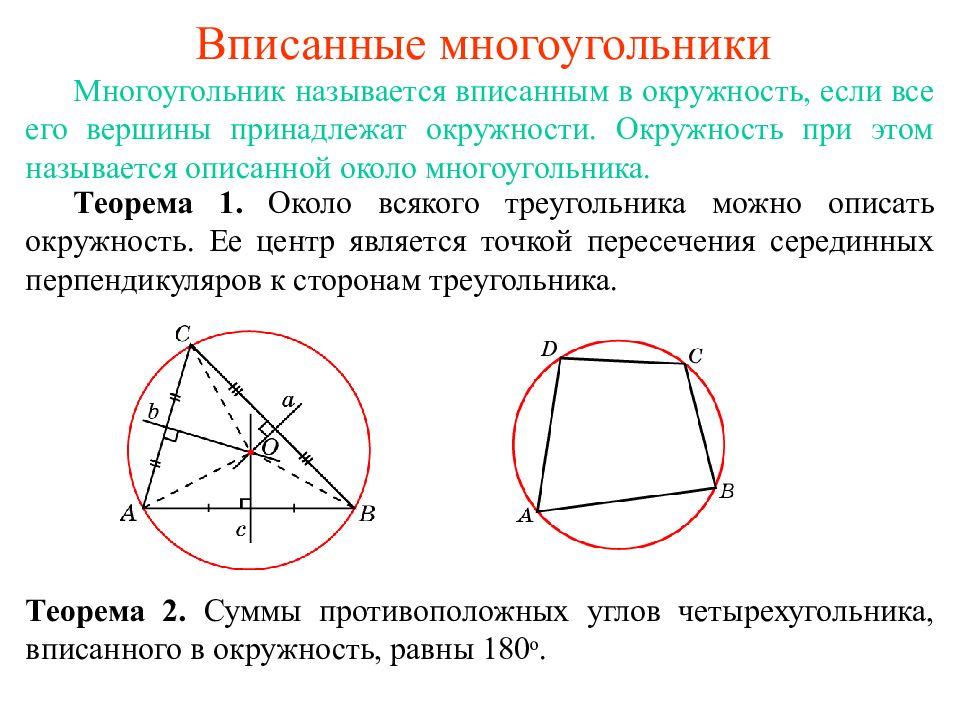
О А В D С Теорема о вписанном угле Какие свойства нам пригодятся при решении задач о вписанном четырехугольнике и описанной окружности?
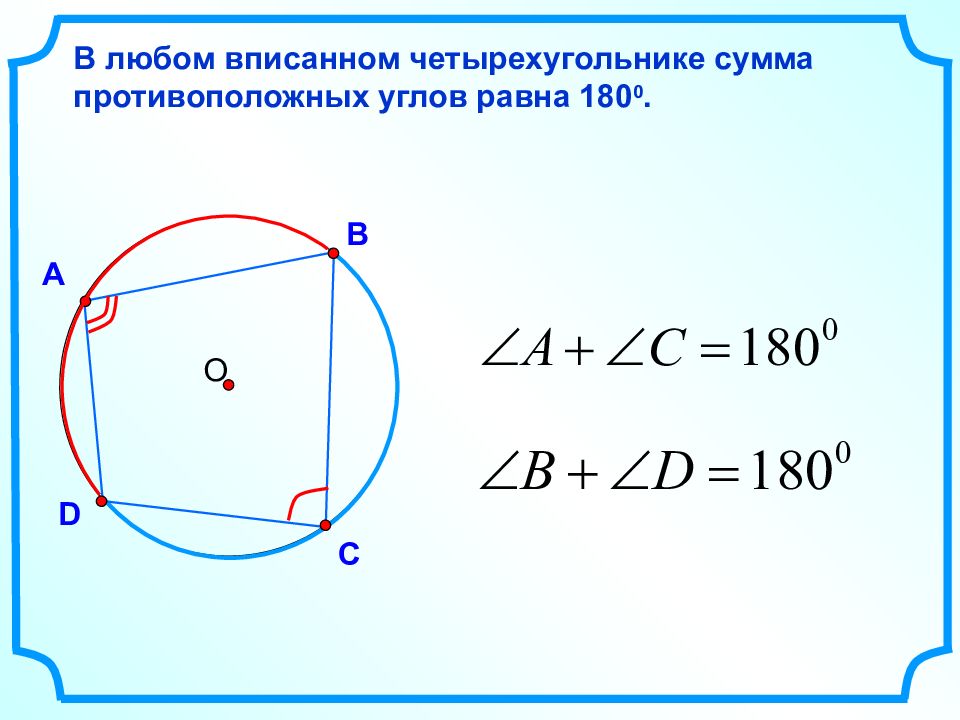
О А В D В любом вписанном четырехугольнике сумма противоположных углов равна 180 0. С
Формула для радиуса окружности, описанной около правильного n- угольника n =3 n =4 n =6 Формула для радиуса окружности, вписанной в правильный n- угольник
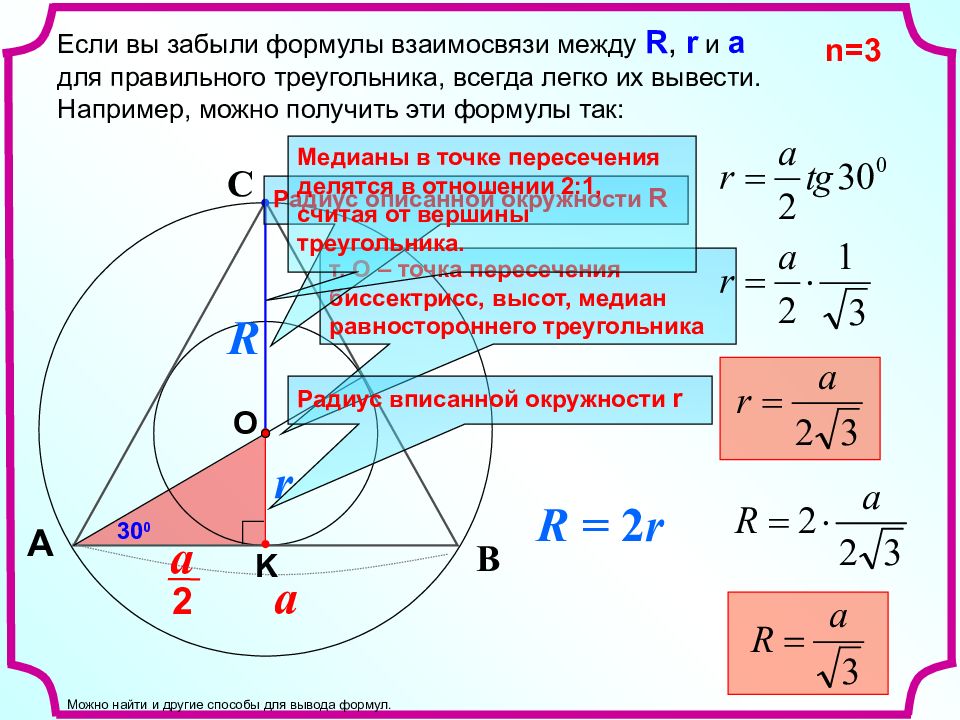
Если вы забыли формулы взаимосвязи между R, r и a для правильного треугольника, всегда легко их вывести. Например, можно получить эти формулы так: r С В A R a a 2 30 0 K O т. О – точка пересечения биссектрисс, высот, медиан равностороннего треугольника Радиус описанной окружности R Радиус вписанной окружности r Медианы в точке пересечения делятся в отношении 2:1, считая от вершины треугольника. R = 2 r Можно найти и другие способы для вывода формул. n =3
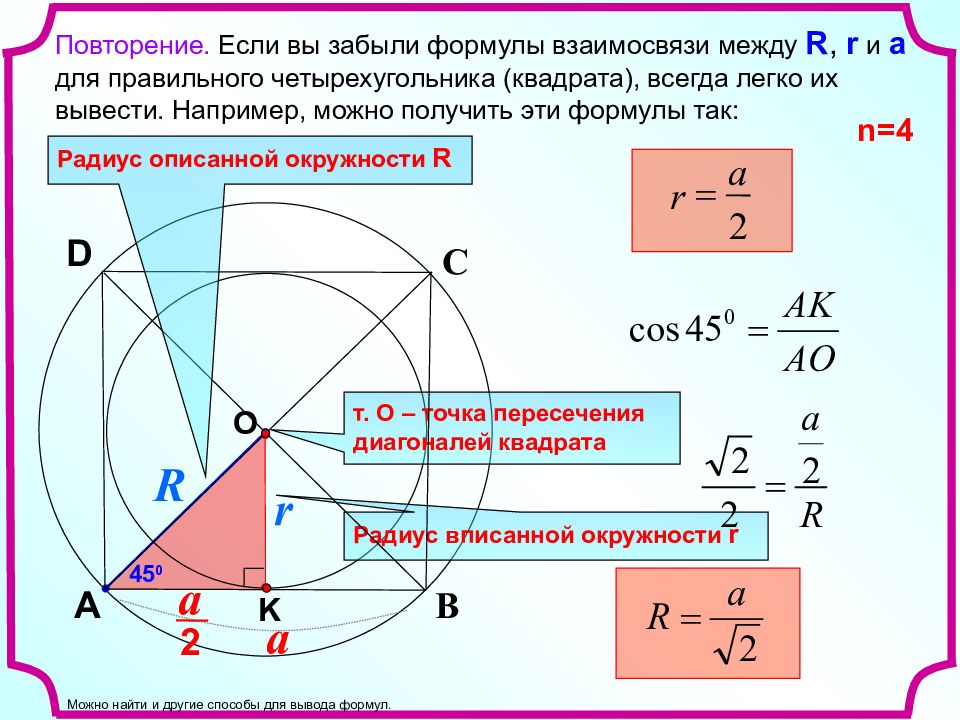
Повторение. Если вы забыли формулы взаимосвязи между R, r и a для правильного четырехугольника (квадрата), всегда легко их вывести. Например, можно получить эти формулы так: r С В A R a a 2 45 0 K т. О – точка пересечения диагоналей квадрата Радиус вписанной окружности r D O 2 a r = Радиус описанной окружности R n =4 Можно найти и другие способы для вывода формул.
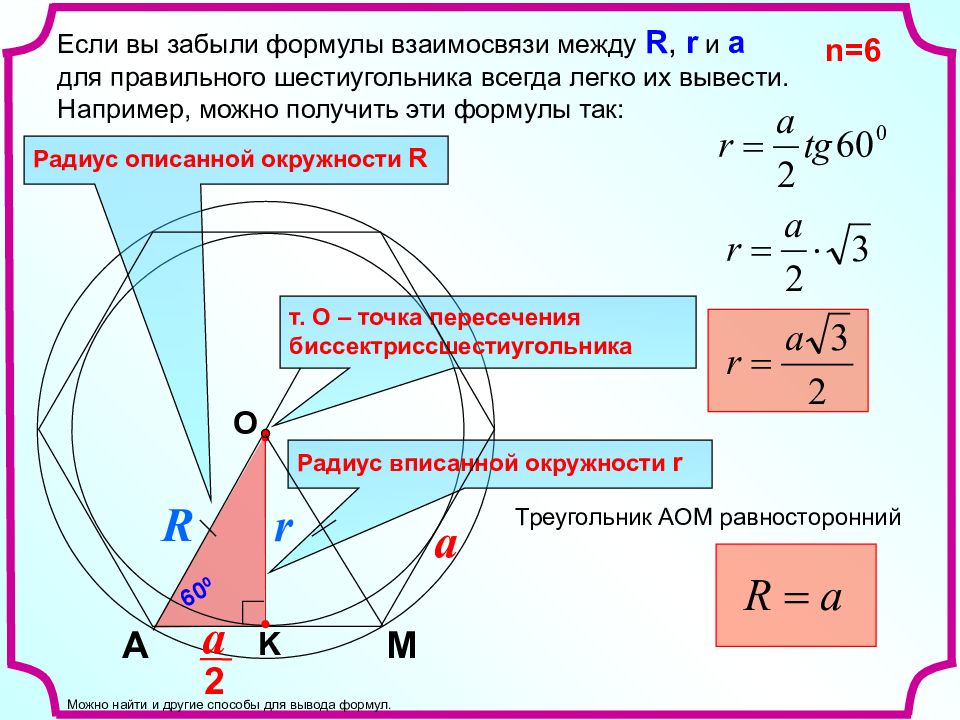
Если вы забыли формулы взаимосвязи между R, r и a для правильного шестиугольника всегда легко их вывести. Например, можно получить эти формулы так: r A R a a 2 6 0 0 т. О – точка пересечения биссектриссшестиугольника Радиус описанной окружности R Радиус вписанной окружности r n =6 K O Треугольник АОМ равносторонний М Можно найти и другие способы для вывода формул.
