Первый слайд презентации: Элементы теории множеств
В математике нет более общего понятия, чем понятие множества
Слайд 2: Значение теории множеств
Понятия и теоремы теории множеств обладают очень большой общностью (поскольку элементами множеств могут быть объекты различной природы) Понятия теории множеств являются базовыми для большинства математических теорий Теория множеств является фундаментом большинства разделов математики (алгебра, математический анализ, функциональный анализ, теория вероятностей и др.) Теория множеств оказала глубокое влияние на понимание самого предмета математики
Слайд 3: Множество
Понятию множества нельзя дать строго определения. Можно сказать, что множество – это «совокупность», «собрание», «семейство» и т.п. – но это не является математическим определением Нужно указать, частным случаем какого более общего понятия оно является, но в математике нет более общего понятия, чем множество. Поэтому приходится иллюстрировать это понятие на примерах, говорить о некоторых вещах, объединенных одним признаком: множество всех студентов в институте, множество планет Солнечной системы, множество четных чисел, множество точек данной окружности и т.д.
Слайд 4: Множество
- это совокупность каких-либо предметов, объектов, которые рассматриваются как единое целое «Множество – многое, мыслимое как единое целое» (Георг Кантор, немецкий математик, основоположник теории множеств) Обозначают множество заглавными латинскими буквами А,В,С и т.д. Объекты, которые составляют множество, обозначают строчными латинскими буквами a,b,c и т.д. Если элемент а принадлежит множеству А, то это обозначается
Слайд 5: Способы задания множеств
Словесное описание ( четные однозначные числа) Перечисление элементов A={2;4;6;8} При помощи характеристического свойства (свойство, присущее элементам этого множества и только им) A={x|P(x)}, например A={x|x=2n, n N,x<10}
Слайд 6: Множество
Один и тот же объект может быть элементом различных множеств (жительница Взлетки является элементом множества всех жителей г.Красноярска, множества всех женщин, множества всех людей и т.п.) В одном множестве не может быть двух одинаковых объектов Если множество состоит из конечного числа элементов, то его называют Конечное (множество дней недели), а если в нем бесконечно много элементов, - то Бесконечное (множество натуральных чисел)
Слайд 7: Множество
Русское слово «множество» может ввести в заблуждение. Оно предполагает некоторое изобилие. Математическое понятие «множество» этого оттенка может не иметь. Существуют множества состоящие из одного, двух элементов. Существуют множества, совсем не имеющее элементов – Пустое множество Если каждый элемент множества В является также элементом множества А, то говорят, что множество В является подмножеством множества А B A
Слайд 8: Множество
Любое множество является подмножеством самого себя A A Пустое множество является подмножеством любого множества Таким образом, для любого множества А всегда существуют два подмножества – пустое и само множество А. Они называются несобственными подмножествами Подмножества множества А, отличные от А и от называются собственными подмножествами
Слайд 9: Равенство множеств
множества А и В равны А=В если каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А, т.е. одновременно А В и В А
Слайд 10: Операции над множествами
Объединением (суммой) множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В. Диаграмма Эйлера-Венна
Слайд 11: Операции над множествами
Пересечением (произведением) множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат и множеству А, и множеству В Диаграмма Эйлера-Венна
Слайд 12: Операции над множествами
Разностью множеств А и В называется множество, состоящее из тех и только тех элементов множества А, которые не содержатся в множестве В Диаграмма Эйлера-Венна
Слайд 13: Операции над множествами
Дополнение множества В до множества А (при условии, что В А) – это разность множеств А\В Диаграмма Эйлера-Венна
Слайд 14: Задача 1
Пусть А= {1; 2 ; 3 ; 4 ; 5 }, B={2;4;6;8;10} Определить, являются ли множества А и В равными ? Найти пересечение, объединение и разность множеств А и В Равны ли множества В\А и А\В ? Найти дополнение множества В до множества А Самостоятельно решить задачи 1-3, стр.15
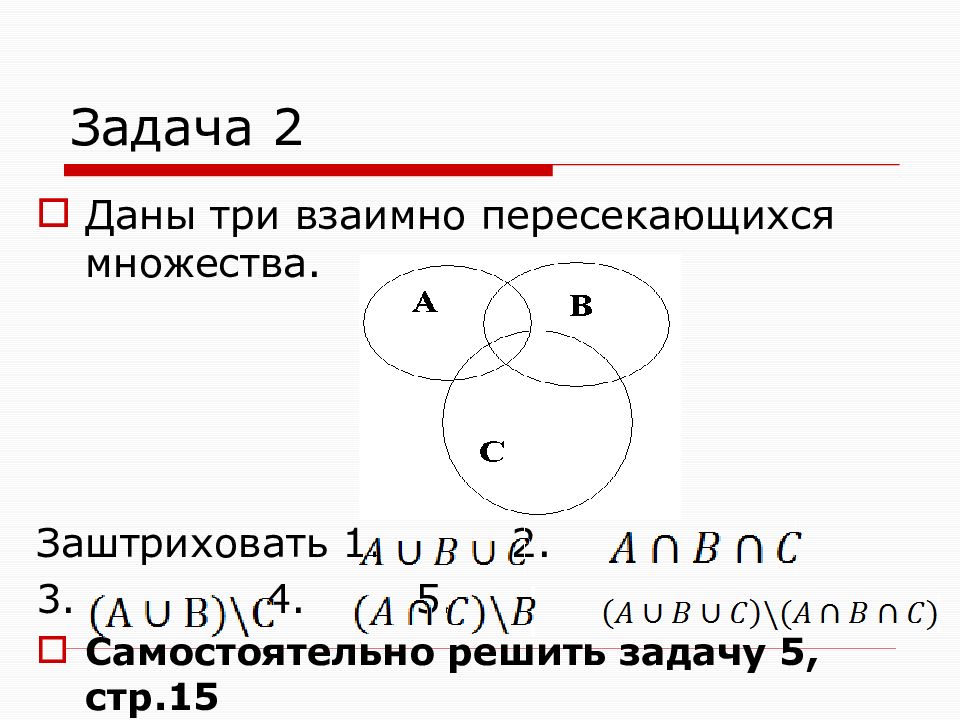
Слайд 15: Задача 2
Даны три взаимно пересекающихся множества. Заштриховать 1. 2. 3. 4. 5. Самостоятельно решить задачу 5, стр.15
Слайд 16: Свойства операций над множествами
Операции с пустым множеством Коммутативность объединения Коммутативность пересечения Ассоциативность объединения Ассоциативность пересечения
Слайд 17: Свойства операций над множествами
Дистрибутивность объединения относительно пересечения Дистрибутивность пересечения относительно объединения Идемпотентность объединения Идемпотентность пересечения Закон поглощения для объединения Закон поглощения для пересечения
Слайд 18: Свойства операций над множествами
Если множество В является подмножеством множества A, то справедливы следующие законы: Если множества В и С являются подмножествами множества А, то справедливы законы (Законы Моргана) Убедиться в справедливости этих законов с помощью диаграмм Эйлера-Венна
Слайд 19: Конечные множества
Множество называется конечным, если оно содержит конечное число элементов. Пусть A – некоторое конечное множество. Обозначим через n(A) количество элементов в множестве A. например, если A={0;1}, то n(A)=2 Число элементов пустого множества равно нулю: Если конечное множество A представимо в виде объединения попарно непересекающихся множеств A 1,A 2,…A N, то n(A)=n( A 1 )+n(A 2 )+…+n(A N ) Для любых двух конечных множеств A и B справедливо равенство (формула включений и исключений)
Слайд 20: Задача 3
В классе 30 учеников. Каждый из них занимается либо футболом, либо хоккеем, а 5 учеников – и хоккеем, и футболом. Сколько учеников занимается футболом, если хоккеем занимается половина класса ? Самостоятельно решить задачи 12, 15, 18 стр.16
Слайд 21: Решение
Пусть A – множество учеников, играющих в футбол, B – в хоккей. Тогда n ( B )=30/2 = 15, Требуется найти n(A) По формуле включений и исключений
Слайд 22: Задача 4
В классе 30 учеников. Известно, что 18 ребят имеют спортивный разряд по лыжам, а 16 – по плаванию. 10 учеников не имеют разряда ни по плаванию, ни по лыжам. Сколько ребят имеют спортивный разряд и по плаванию, и по лыжам? Самостоятельно решить задачу 20 стр.16
Слайд 23: Решение
Решение: Пусть A – множество учеников, имеющих разряд по лыжам, B – множество учеников, имеющих разряд по плаванию. Тогда, n ( A )=18, n ( b )=16, Требуется найти По формуле включений и исключений
Слайд 25: Задача 4
В одном курортном городке проводят свой отпуск 100 отдыхающих. Из них 80 человек принимают минеральные ванны, 70 – сеансы ароматерапии, 60 – сеансы массажа. При этом минеральные ванны и ароматерапию посещают 60, минеральные ванны и массаж – 50, ароматерапию и массаж – 40 человек. На все три процедуры ходят 30 человек. Сколько человек на этом курорте не посещает никаких процедур вообще ? Самостоятельно 17,19, стр.16
Последний слайд презентации: Элементы теории множеств: Задача 5
Каждый из 64 студентов 1-го курса изучают по крайней мере один из 3-х иностранных языков: итальянский, испанский или французский. При этом 28 изучают итальянский, 40 – испанский, а 25 – французский. Французский и испанский изучают 9 студентов, французский и итальянский – 18 студентов, итальянский и испанский – 7 студентов. Сколько студентов изучают ровно два языка из упомянутых выше?