Выполнили: Еремина Дарья Решетникова Кристина Группа МИ-16
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов. Виды соединений (комбинаций) элементов фиксированного(конечного) множества: -перестановки; -размещения; -сочетания.
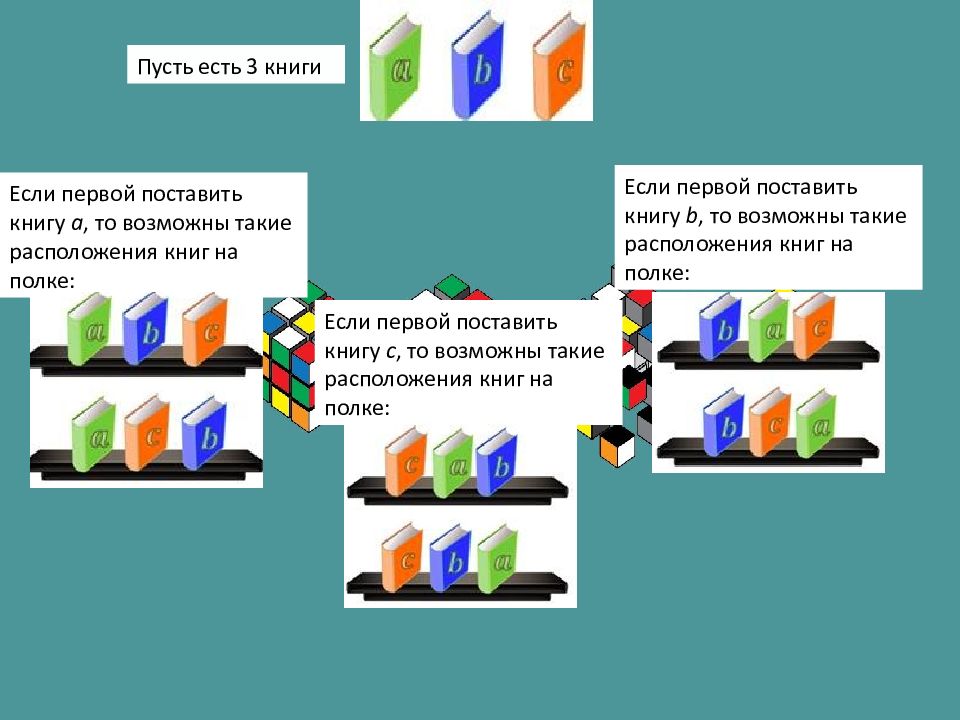
Пусть есть 3 книги Если первой поставить книгу а, то возможны такие расположения книг на полке: Если первой поставить книгу b, то возможны такие расположения книг на полке: Если первой поставить книгу c, то возможны такие расположения книг на полке:
Перестановкой из n элементов называется каждое расположение этих элементов в определённом порядке. Обозначение: P n Формула числа перестановок из n элементов: Пусть у нас есть n элементов. Тогда на первое место можно поставить один из них, то есть n вариантов. На второе место можно поставить любой из оставшихся « n -1» элементов. На третье место можно поставить любой из оставшихся « n -2» элементов. И так далее …. В результате получим следующую запись: P n =1*2*3*…*( n -2)*( n -1)* n
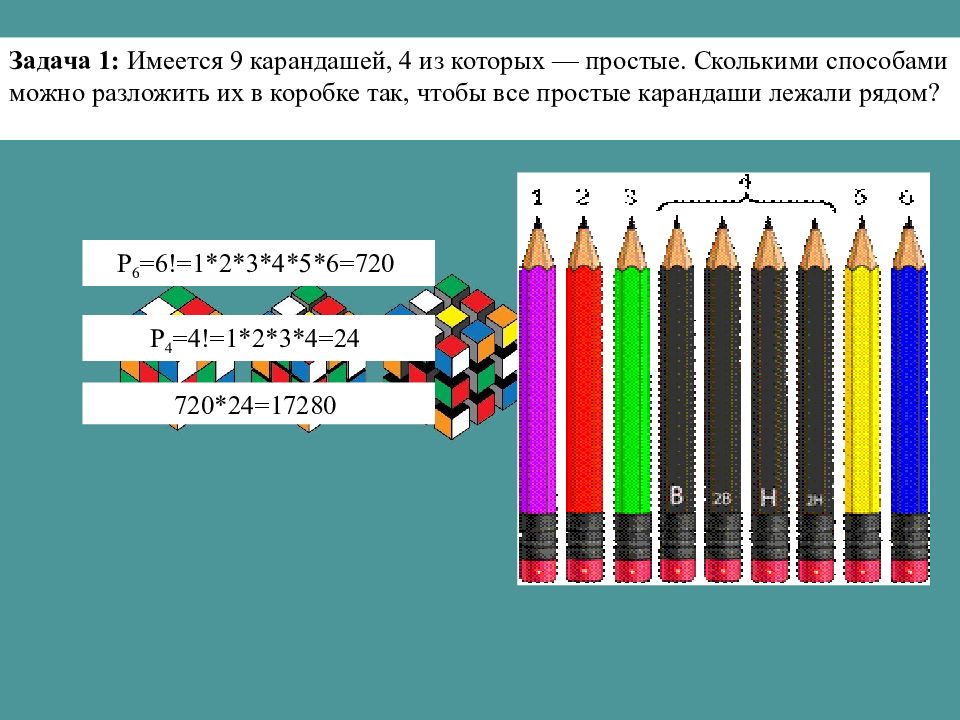
Задача 1: Имеется 9 карандашей, 4 из которых — простые. Сколькими способами можно разложить их в коробке так, чтобы все простые карандаши лежали рядом? P 6 =6!=1*2*3*4*5*6=720 P 4 =4!=1*2*3*4=24 720*24=17280
Задача 2: Сколько существует способов рассадить за круглый стол 5 юношей и 5 девушек так, чтобы они чередовались? P 5 = 5 !=1*2*3*4*5= 120 ( P 5 ) 2 = (5! ) 2 P 5 = 5 !=1*2*3*4*5= 120 2*( P 5 ) 2 =2*(5!) 2 =2*120 2 =14400
