Первый слайд презентации: ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Слайд 2: Работа и мощность переменного тока
В случае, когда сила тока изменяется во времени по произвольному закону, ток называется пере-менным. Колебания тока называются гармоническими, если они описываются уравнениями вида – циклическая частота, ( ω t + φ ) – фаза колебания, φ - начальная фаза, I m – амплитуда силы тока.
Слайд 3
В цепях переменного тока возникает разность фаз в колебаниях силы тока и напряжения, которая зависит от параметров ω, L, C, R. С учетом этого уравнения колебаний для некоторого участка цепи запишем в виде Мгновенная мощность тока на этом участке Преобразуем произведение синусов.
Слайд 4
Практический интерес представляет среднее значение мощности тока за период колебаний. При этом учтем, что среднее значение cos(2 ω t – φ ) равно нулю. Тогда – действующие значения силы тока и напряжения.
Слайд 5
Работа тока на участке цепи за время t Если на участке цепи имеется только резистор, то φ = 0, и средняя мощность тока
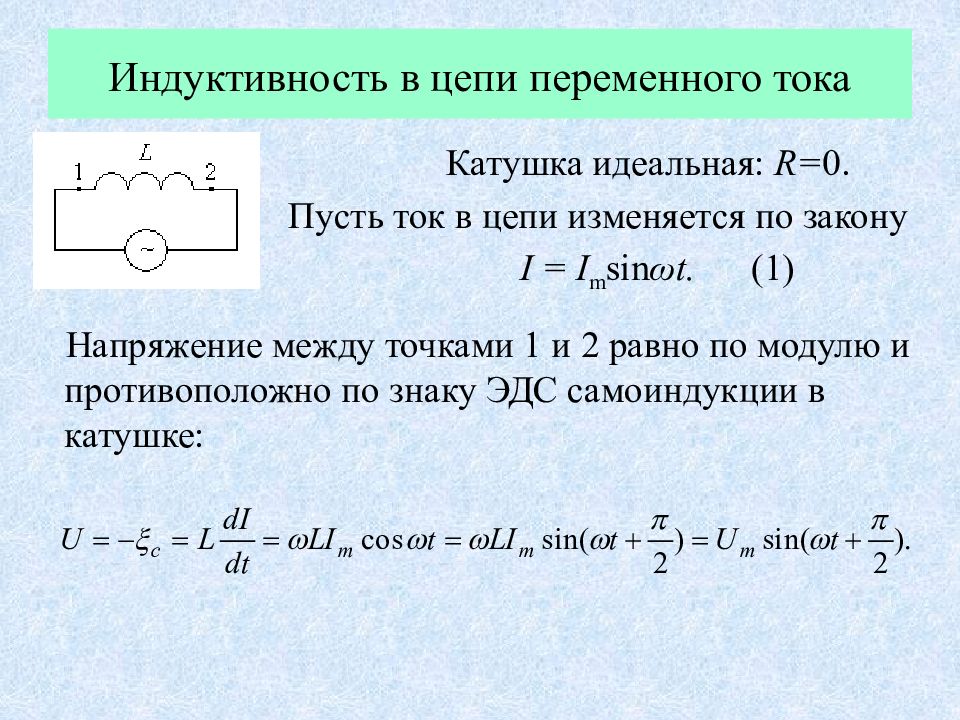
Катушка идеальная: R= 0. Пусть ток в цепи изменяется по закону I = I m sin ω t. (1) Напряжение между точками 1 и 2 равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Слайд 7
А нализ: 1. Напряжение опережает силу тока на φ = π / 2. 2. Амплитудные значения силы тока и напряжения связаны соотношением U m = I m · ω L X L = ω L - индуктивное сопротивление катушки. 3. Мощность тока в цепи
Слайд 8: Емкость в цепи переменного тока
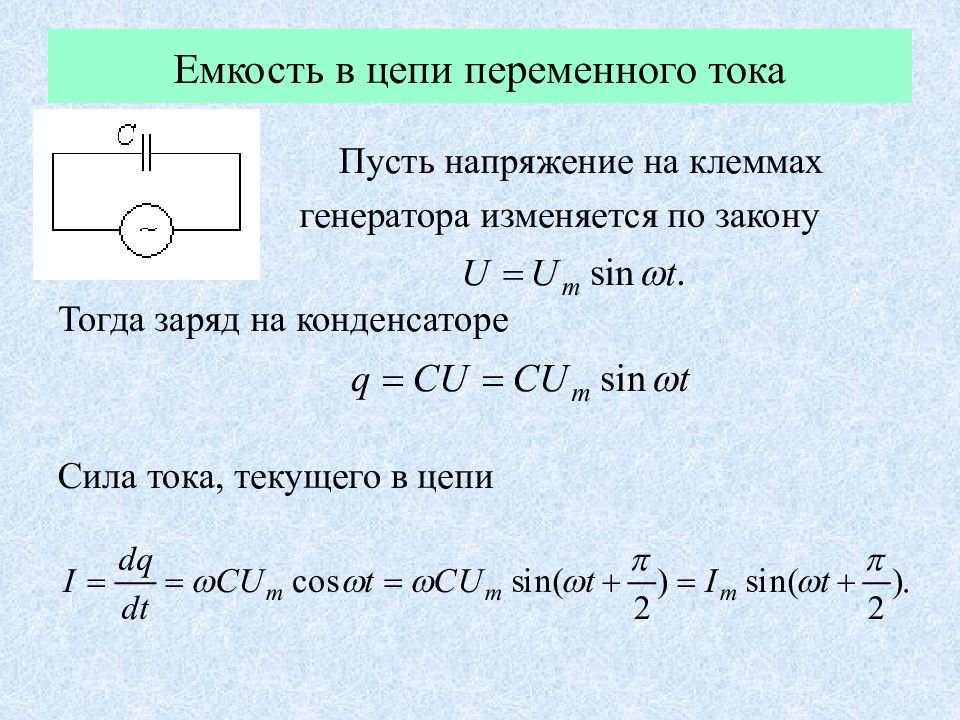
Пусть напряжение на клеммах генератора изменяется по закону Тогда заряд на конденсаторе Сила тока, текущего в цепи
Слайд 9
Анализ: 1. Сила тока, изменяясь, опережает напряжение на φ = π / 2. 2. Амплитудные значения силы тока и напряжения связаны соотношением - емкостное сопротивление цепи. 3. Средняя мощность тока в цепи равна нулю ( cos φ = 0).
Слайд 10: Электрический колебательный контур
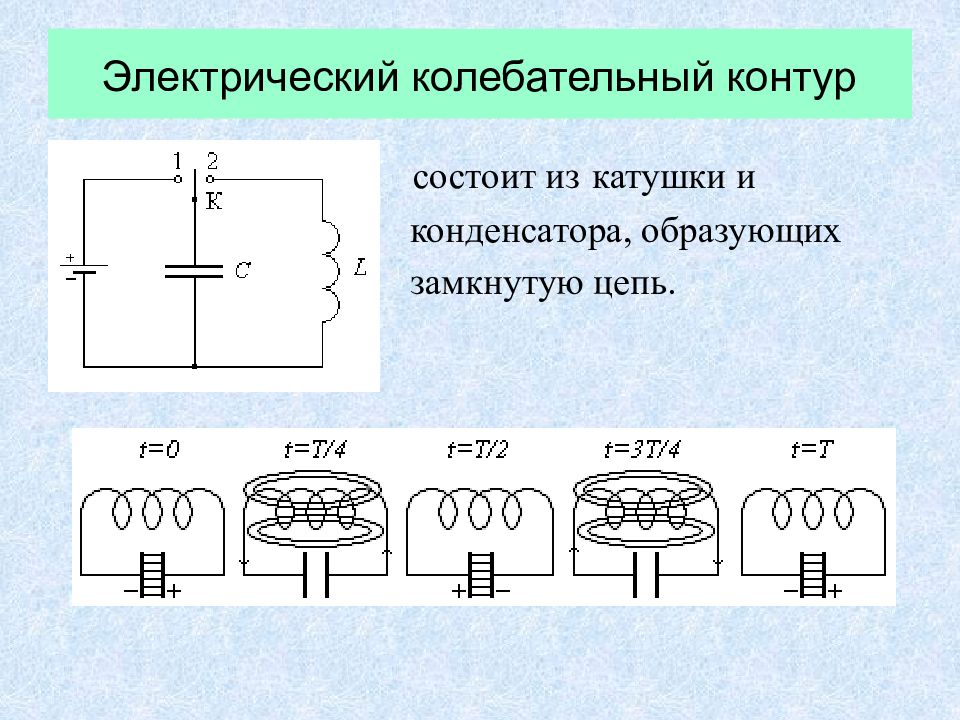
состоит из катушки и конденсатора, образующих замкнутую цепь.
Слайд 11
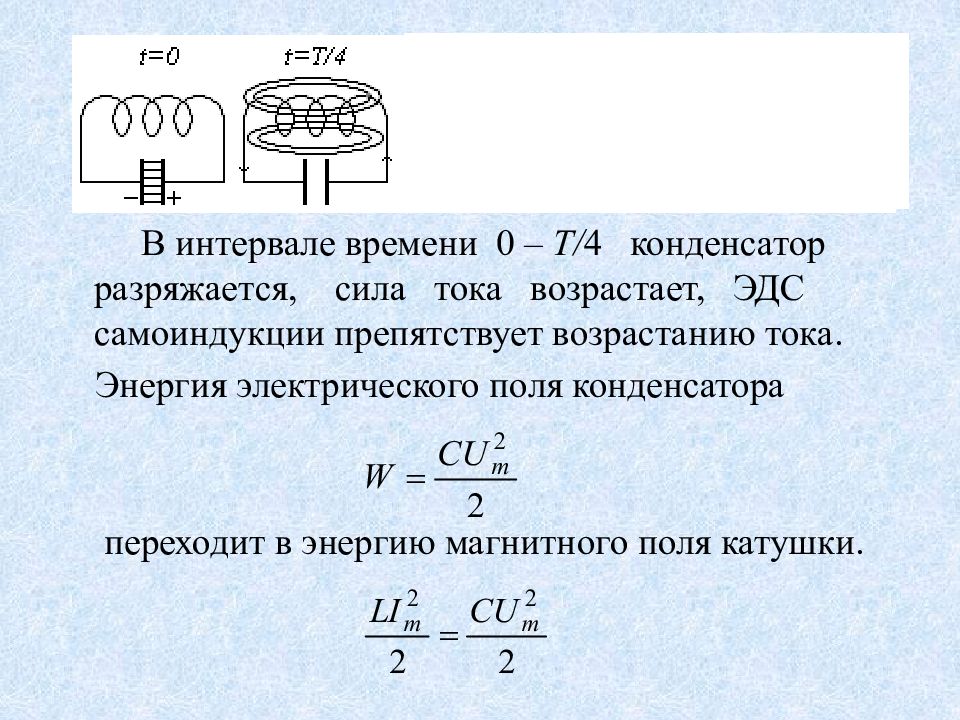
В интервале времени 0 – Т/ 4 конденсатор разряжается, сила тока возрастает, ЭДС самоиндукции препятствует возрастанию тока. Энергия электрического поля конденсатора переходит в энергию магнитного поля катушки.
Слайд 12
В интервале времени Т /4 – Т /2 сила тока уменьшается, ЭДС самоиндукции поддерживает убывающий ток. В результате происходит перезарядка конденсатора. При этом энергия магнитного поля катушки переходит в энергию электрического поля конденсатора.
Слайд 13
Теоретическое рассмотрение дает: В идеальном контуре, содержащем конденса-тор и катушку индуктивности, должны проис-ходить незатухающие электромагнитные колебания, циклическая частота которых 2. Период собственных колебаний в контуре (Формула У.Томсона).
Слайд 14
Полная энергия идеального контура с течением времени не изменяется: q, I – мгновенные значения заряда на конденса-торе и силы тока в контуре. Для амплитудных значений справедливо равенство
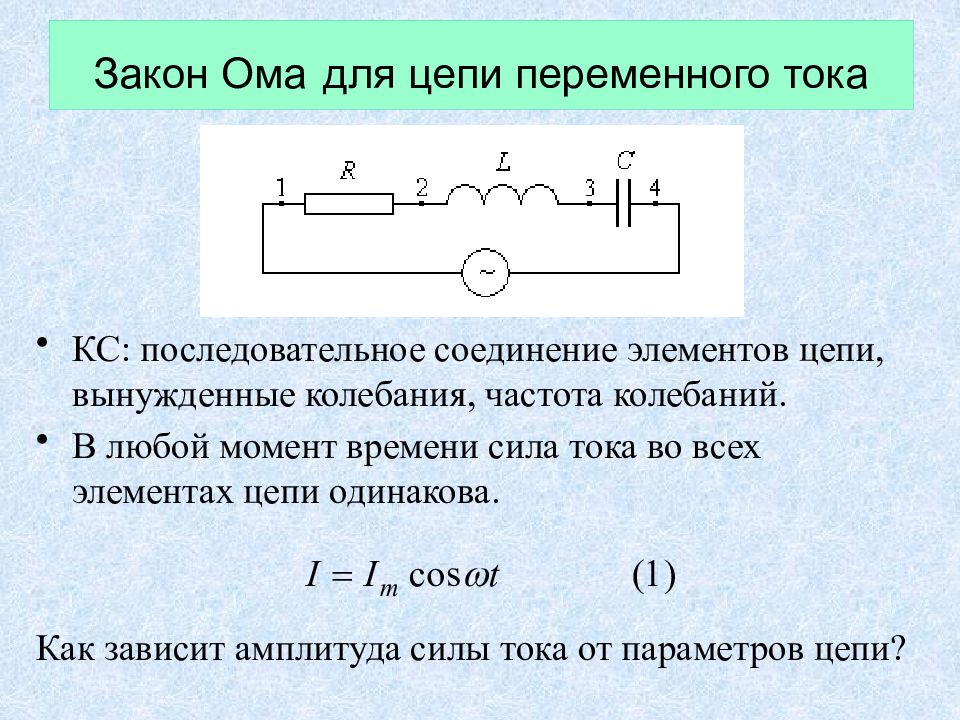
Слайд 15: Закон Ома для цепи переменного тока
КС: последовательное соединение элементов цепи, вынужденные колебания, частота колебаний. В любой момент времени сила тока во всех элементах цепи одинакова. Как зависит амплитуда силы тока от параметров цепи?
Слайд 16
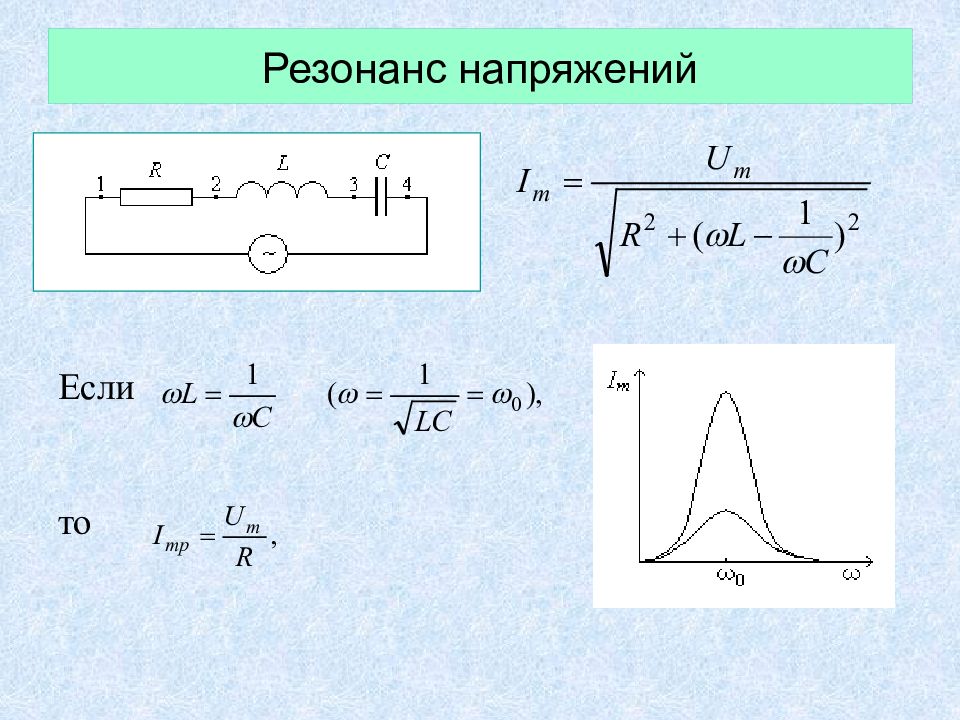
Решение задачи с использованием метода векторных диаграмм приводит к следующему результату:
Слайд 17
Выражение (2) – закон Ома для последовательной цепи переменного тока. Величина имеет смысл полного сопротивления цепи.
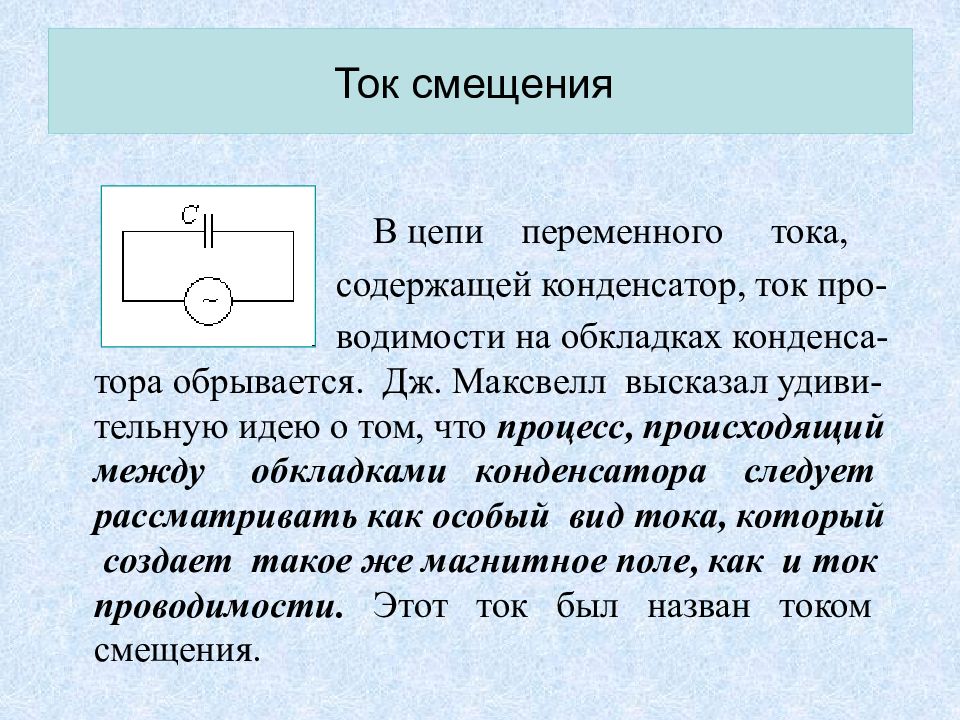
Слайд 20: Ток смещения
В цепи переменного тока, содержащей конденсатор, ток про- водимости на обкладках конденса-тора обрывается. Дж. Максвелл высказал удиви-тельную идею о том, что процесс, происходящий между обкладками конденсатора следует рассматривать как особый вид тока, который создает такое же магнитное поле, как и ток проводимости. Этот ток был назван током смещения.
Слайд 21
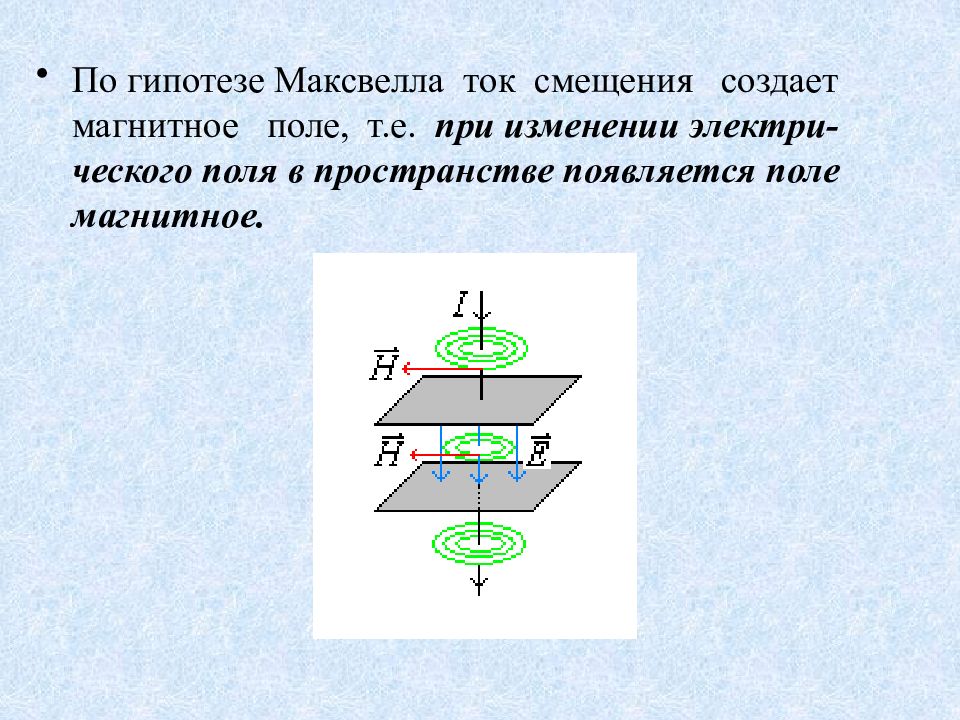
По гипотезе Максвелла ток смещения создает магнитное поле, т.е. при изменении электри-ческого поля в пространстве появляется поле магнитное.
Слайд 22
Наиболее весомый вклад внес в молекулярную физику и электродина-мику. В 1859 г. установил статистический закон, описывающий распреде-лени молекул газа по скоростям. В 1860-65 гг. создал теорию электро-магнитного поля. В 1865 г. теоретически обосновал существование ЭМ волн и высказал гипотезу об ЭМ природе света. Максвелл Джеймс Клерк (1831 – 1879, англ.)
Слайд 23
Переменный электромагнитный процесс распространяется в пространстве. Он имеет волновой характер. Вывод о существовании электромагнитных волн Дж. Максвелл сделал в 186 5 г. Г.Герц экспериментально обнаружил электро-магнитные волны и исследовал их свойства в 1887-88 гг.
Слайд 24
Является одним из осно-воположников электро-динамики. В 1888 г. экспериментально доказал существование электромагнитных волн Придал уравнениям Максвелла современную форму. В 1887 г. обнару-жил внешний фотоэф-фект. Генрих Герц (1857 – 1894, нем.)
Слайд 25
Следствия из уравнений Максвелла (в дифферен-циальной форме): 1. Скорость распространения ЭМВ: с ≈ 3 · 10 8 м/с.
Слайд 26
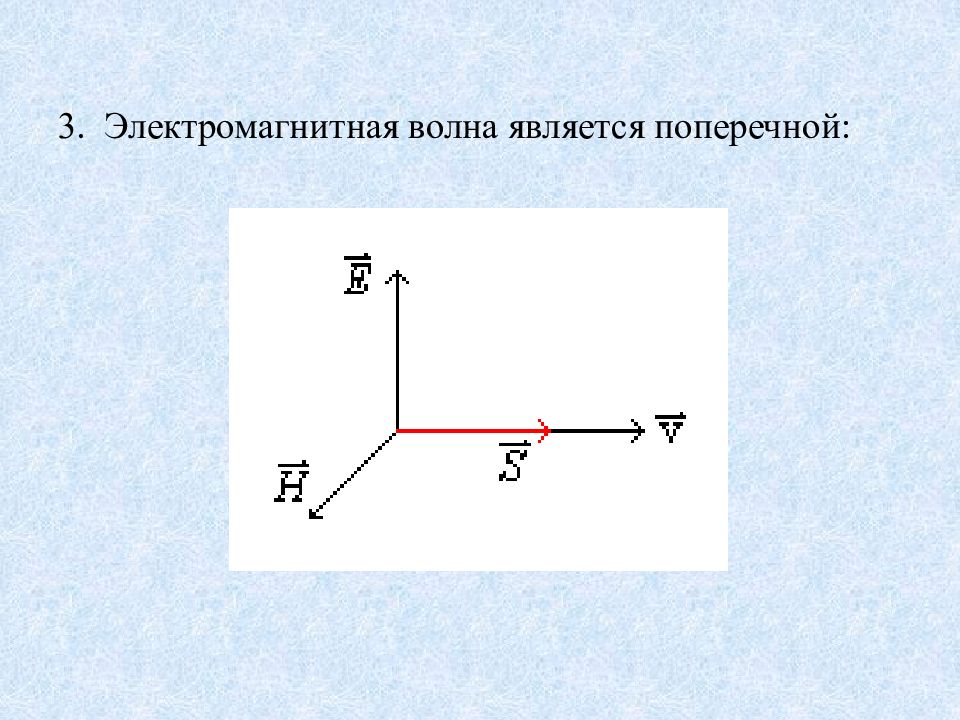
2. Вектор Умова-Пойнтинга для ЭМВ (определяет мгновенное значение энергии, переносимой волной за единицу времени через единичную площадку): S = S ( t ). Интенсивность ЭМВ – среднее значение S.
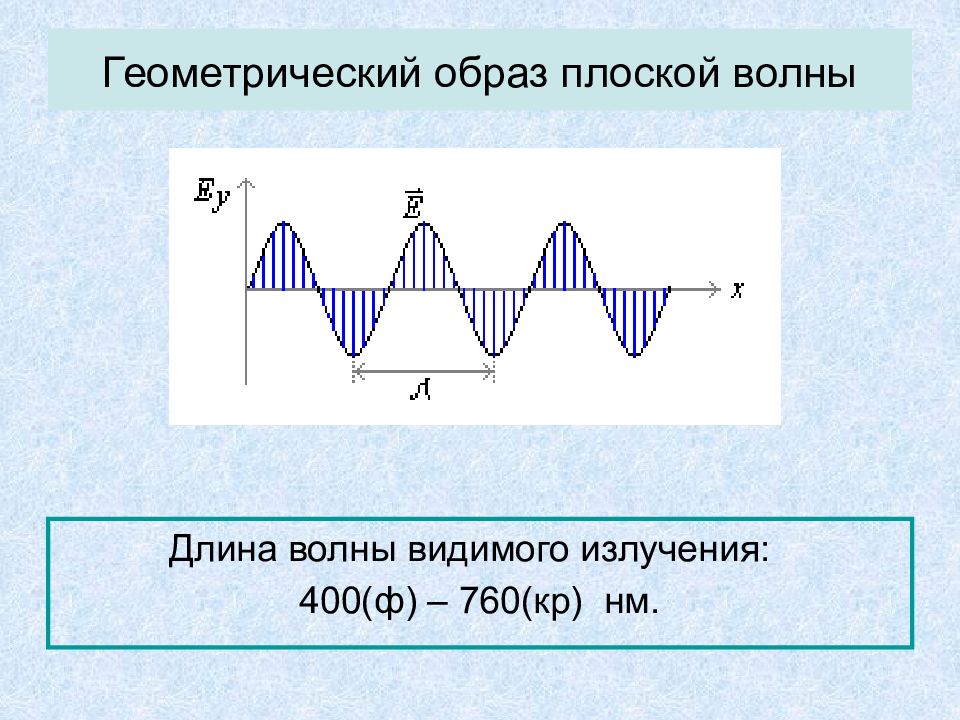
Слайд 28: Геометрический образ плоской волны
Длина волны видимого излучения: 400(ф) – 760(кр) нм.
Слайд 29
4. ЭМВ производит давление на тела. В 1873 г. Дж. Максвелл рассчитал давление света на основе электромагнитной теории: Здесь I - интенсивность ЭМВ, r - коэффициент ее отражения. Справедливость этой формулы была эксперимен-тально подтверждена выдающимся русским физиком П.Н.Лебедевым в 1898 г.
Слайд 30
П.Н.Лебедев (1866 – 1912, рус.) Известен как блестящий экспериментатор-виртуоз, автор исследований, выполненных скромными средствами на грани технических возможно-стей того времени, но поражающих глубокой интуицией и гениально-стью. .
Последний слайд презентации: ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
5. На границе диэлектриков ЭМВ отражаются и преломляются. Известные законы отражения и преломления света являются прямым следствием уравнений Максвелла. 6. Имеют место такие явления, как поглощение, интерференция, дифракция, дисперсия ЭМВ и др.