Первый слайд презентации: Все о четырехугольниках (теория)
Слайд 2: Содержание
Определения Параллелограмм а) Свойства параллелограмма Прямоугольник, ромб, квадрат а) Свойства прямоугольника, ромба, квадрата Трапеция (определения, виды) а) Свойства трапеции Свойства вписанных и описанных четырёхугольников Формулы площадей а) прямоугольника и квадрата б) параллелограмма в) ромба г) трапеции д) произвольного четырёхугольника
Слайд 3: Определения
Четырёхугольник – это многоугольник с четырьмя вершинами и четырьмя сторонами Соседние вершины – вершины, являющиеся концами одной из сторон четырёхугольника Противолежащие вершины – вершины не являющиеся соседними Диагонали четырёхугольника – отрезки, соединяющие противолежащие вершины. Соседние стороны – стороны, исходящие из одной вершины. Противолежащие стороны – стороны, не являющиеся соседними. Периметр – сумма длин всех сторон четырёхугольника.
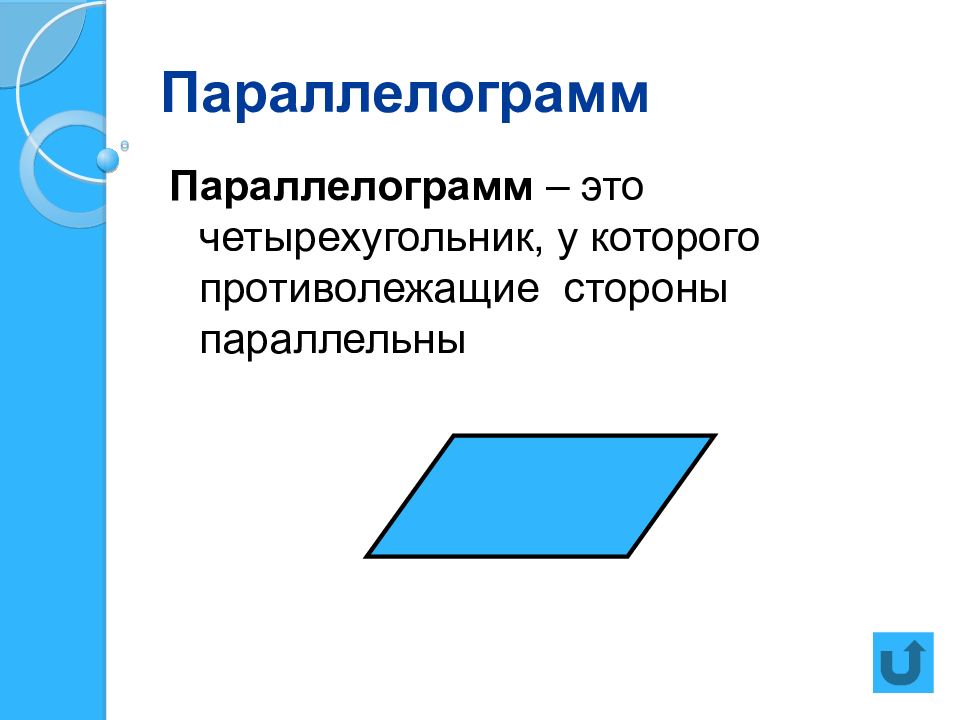
Слайд 4: Параллелограмм
Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны
Слайд 5: Свойства параллелограмма
1. Противолежащие стороны параллелограмма равны 2. Противолежащие углы параллелограмма равны 3. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам Утверждения, обратные свойствам 1-3, являются признаками параллелограмма, т.е. если противолежащие стороны четырёхугольника равны, то этот четырёхугольник - параллелограмм
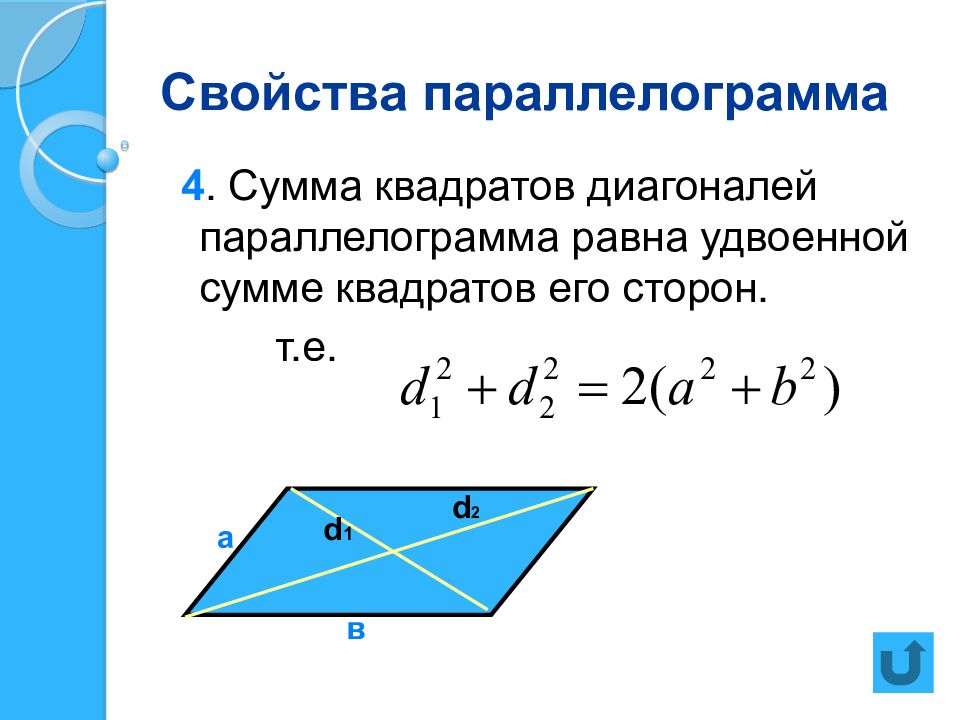
Слайд 6: Свойства параллелограмма
4. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон. т.е. d 1 d 2 а в
Слайд 7: Прямоугольник, ромб, квадрат
Прямоугольник - это параллелограмм, у которого все углы прямые Ромб – это параллелограмм, у которого все стороны равны. Квадрат – это прямоугольник, у которого все стороны равны. Квадрат – это ромб, у которого все углы прямые.
Слайд 8: Свойства прямоугольника, ромба и квадрата
1. Диагонали прямоугольника равны. 2. Диагонали ромба пересекаются под прямым углом. 3. Диагонали ромба являются биссектрисами его углов. 4. Диагонали квадрата: 1) равны 2) пересекаются под прямым углом 3) являются биссектрисами его углов
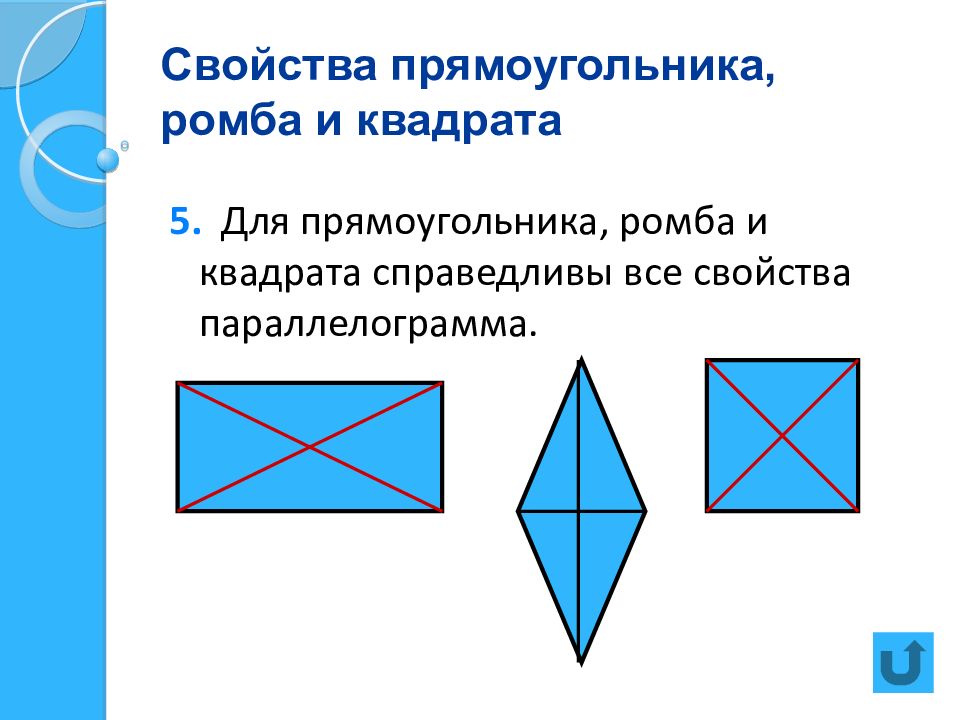
Слайд 9: Свойства прямоугольника, ромба и квадрата
5. Для прямоугольника, ромба и квадрата справедливы все свойства параллелограмма.
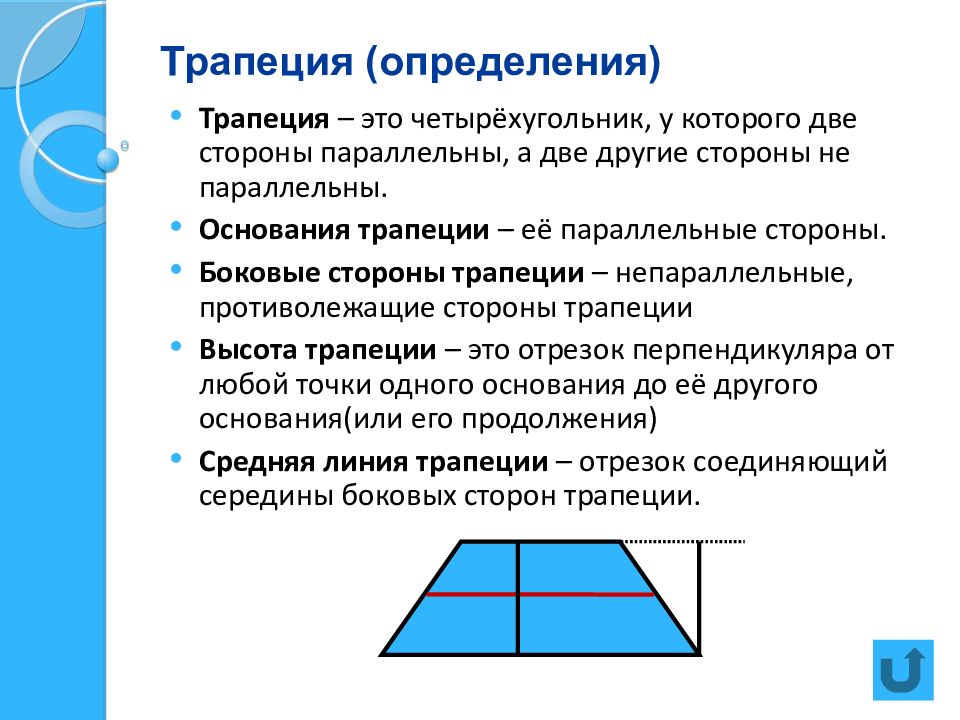
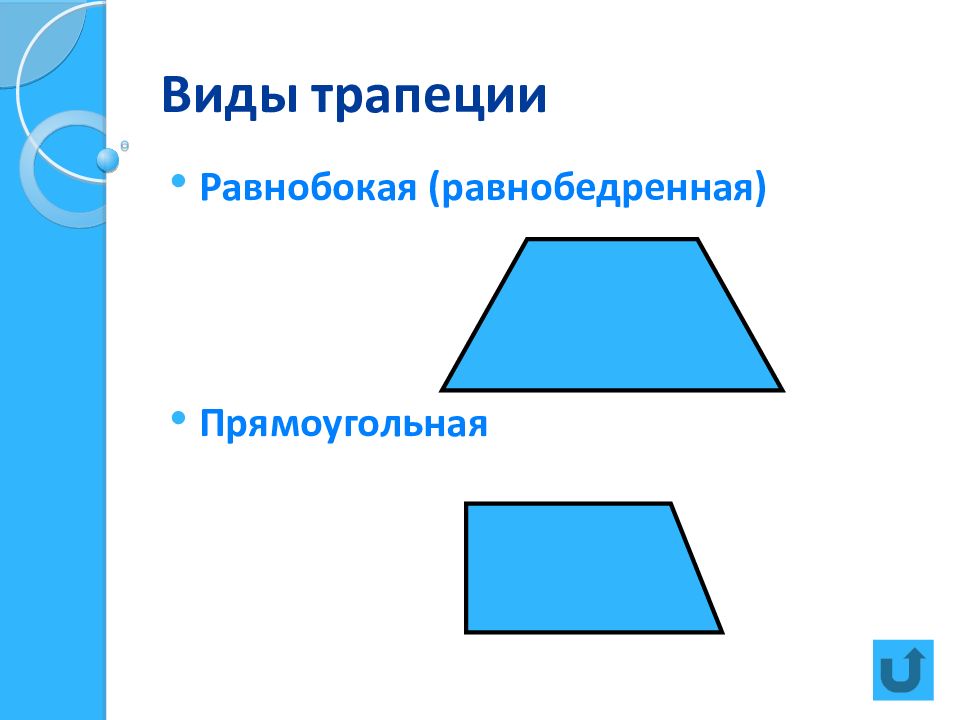
Слайд 10: Трапеция (определения)
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основания трапеции – её параллельные стороны. Боковые стороны трапеции – непараллельные, противолежащие стороны трапеции Высота трапеции – это отрезок перпендикуляра от любой точки одного основания до её другого основания(или его продолжения) Средняя линия трапеции – отрезок соединяющий середины боковых сторон трапеции.
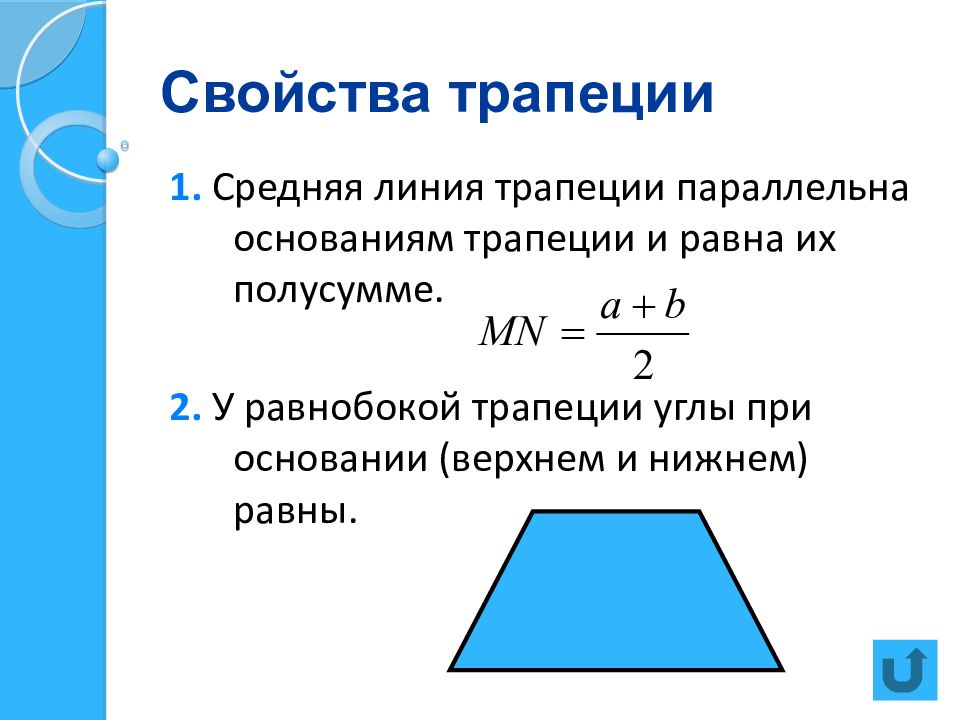
Слайд 12: Свойства трапеции
1. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме. 2. У равнобокой трапеции углы при основании (верхнем и нижнем) равны.
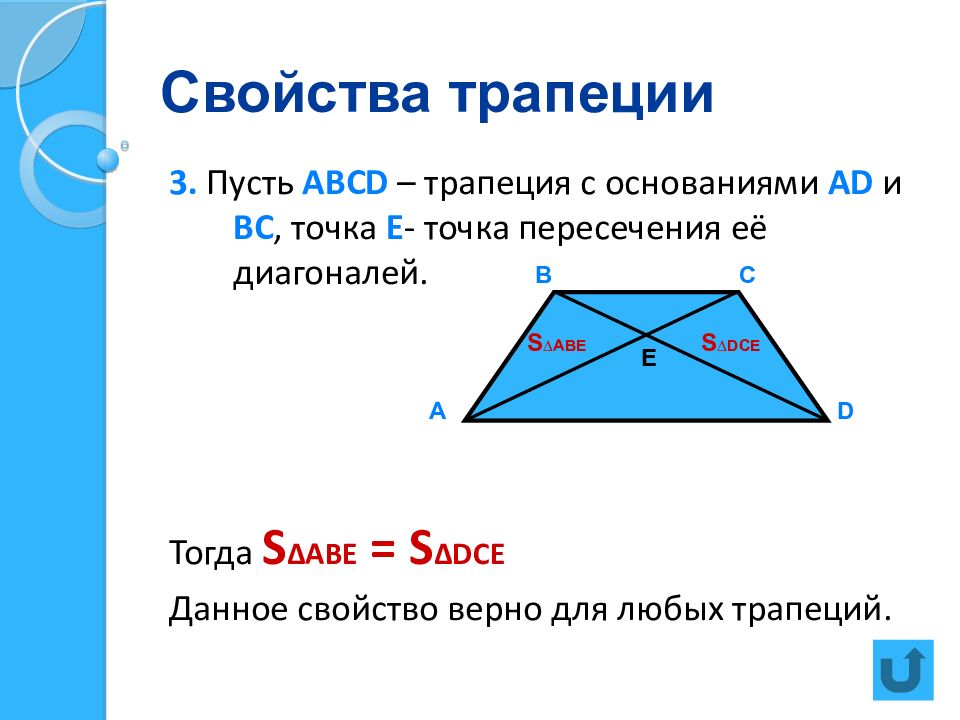
Слайд 13: Свойства трапеции
3. Пусть АВС D – трапеция с основаниями А D и ВС, точка Е - точка пересечения её диагоналей. Тогда S ∆ АВЕ = S ∆D СЕ Данное свойство верно для любых трапеций. А В С D Е S ∆ АВЕ S ∆D СЕ
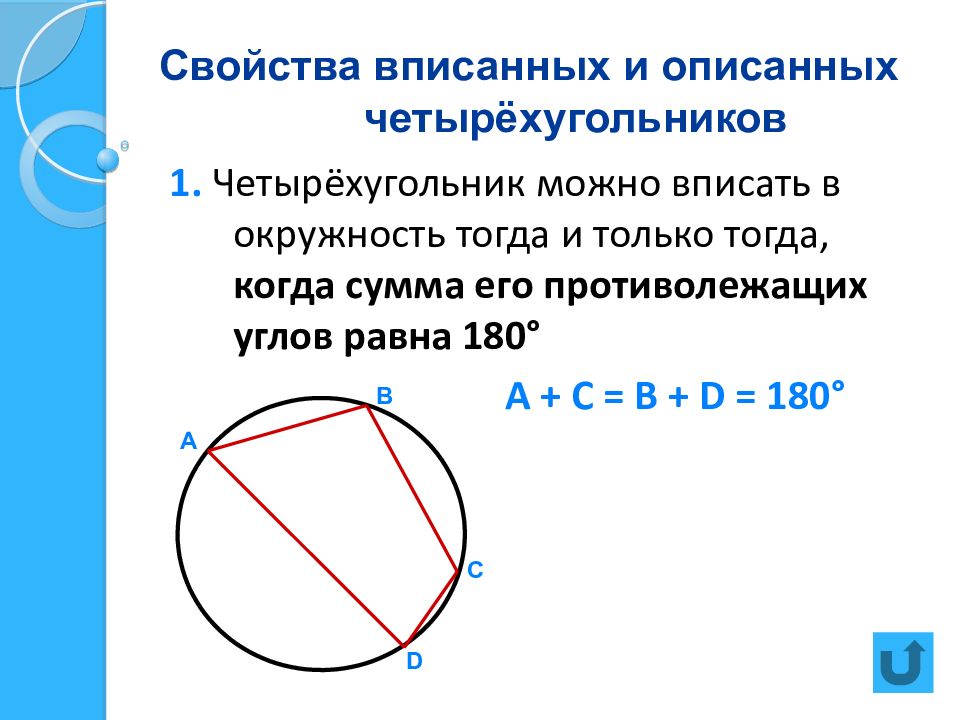
Слайд 14: Свойства вписанных и описанных четырёхугольников
1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180 ° А + С = В + D = 180 ° А В С D
Слайд 15: Свойства вписанных и описанных четырёхугольников
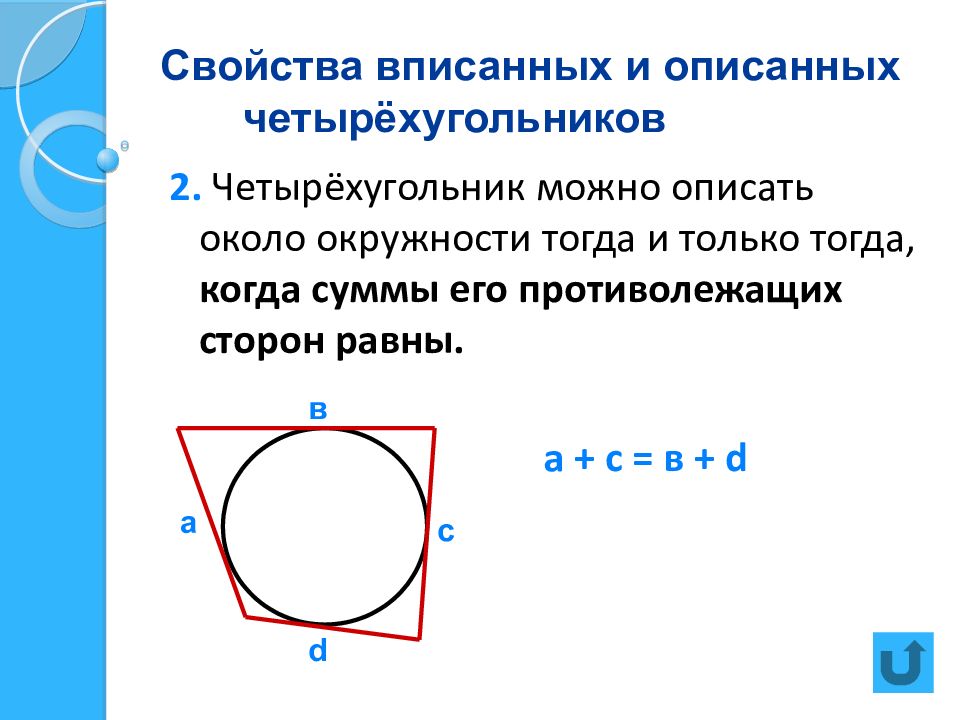
2. Четырёхугольник можно описать около окружности тогда и только тогда, когда суммы его противолежащих сторон равны. а + с = в + d а в с d
Слайд 16: Свойства вписанных и описанных четырёхугольников
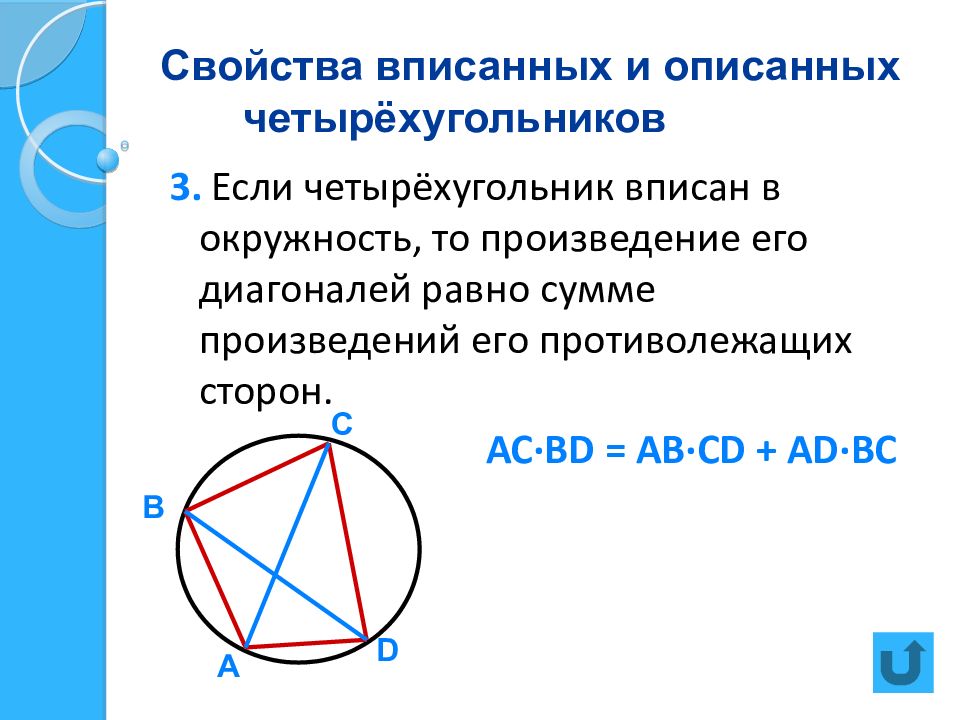
3. Если четырёхугольник вписан в окружность, то произведение его диагоналей равно сумме произведений его противолежащих сторон. АС · В D = АВ · С D + А D· ВС А В С D
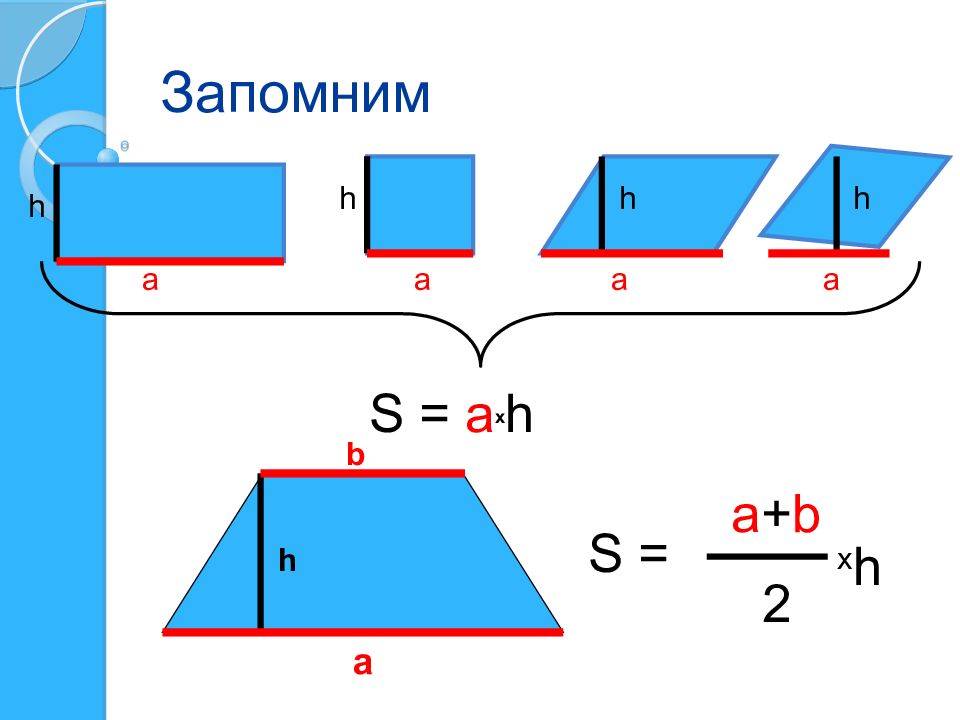
Слайд 17: Формулы площадей четырёхугольников
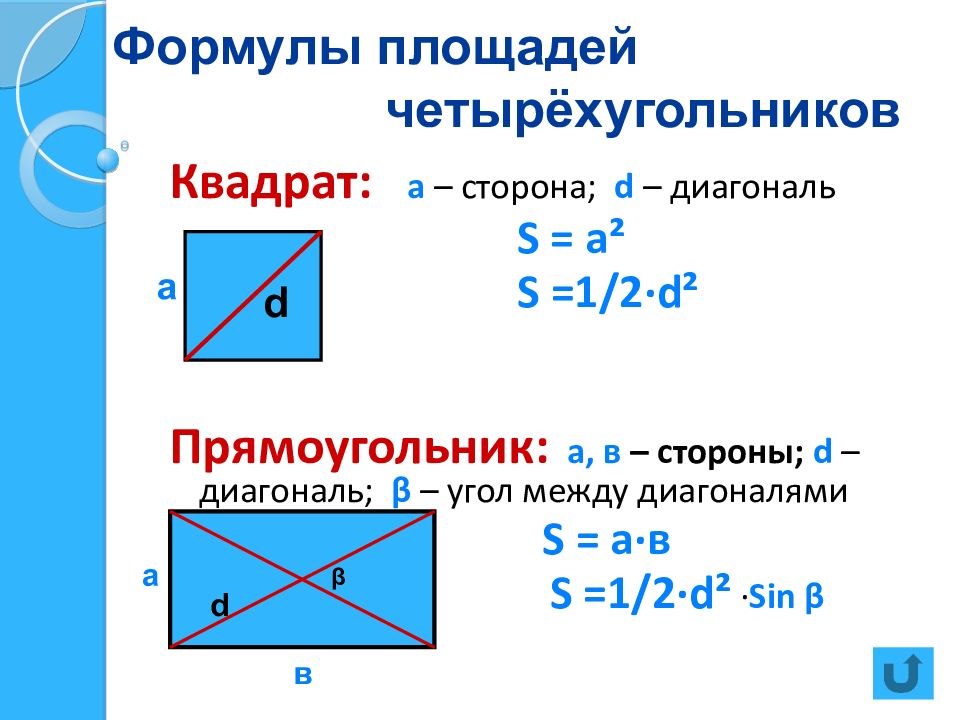
Квадрат: а – сторона; d – диагональ S = a² S =1 / 2·d² Прямоугольник: а, в – стороны; d – диагональ; β – угол между диагоналями S = a· в S =1 / 2·d² · Sin β а d а в β d
Слайд 18: Формулы площадей четырёхугольников
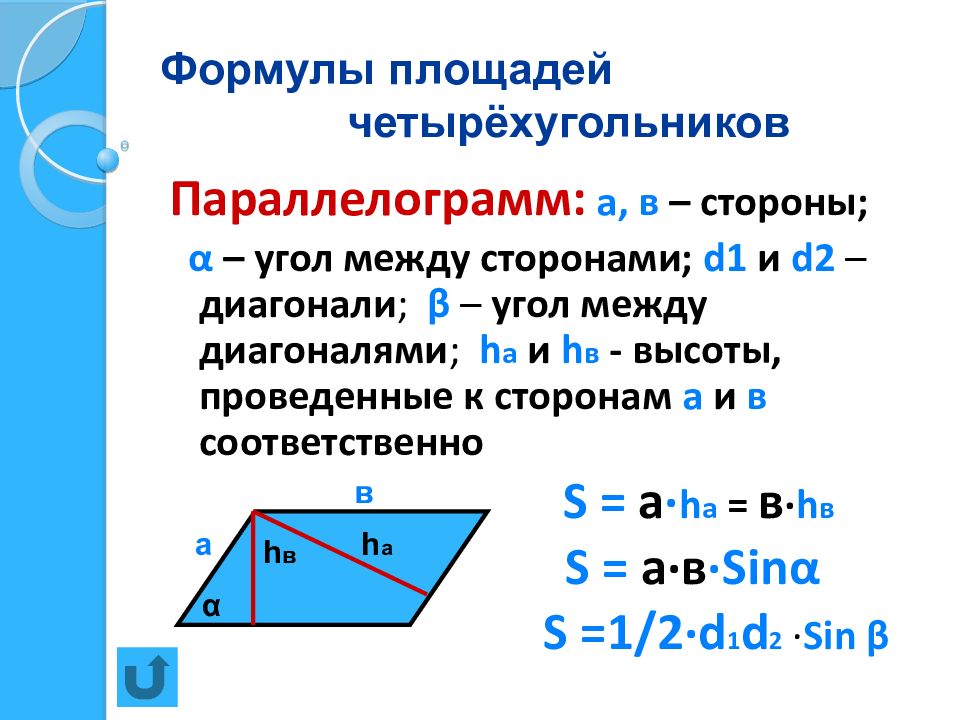
Параллелограмм: а, в – стороны; α – угол между сторонами; d1 и d2 – диагонали ; β – угол между диагоналями ; h a и h в - высоты, проведенные к сторонам а и в соответственно S = a · h a = в · h в S = a· в ·Sin α S =1 / 2·d 1 d 2 · Sin β а в α h a h в
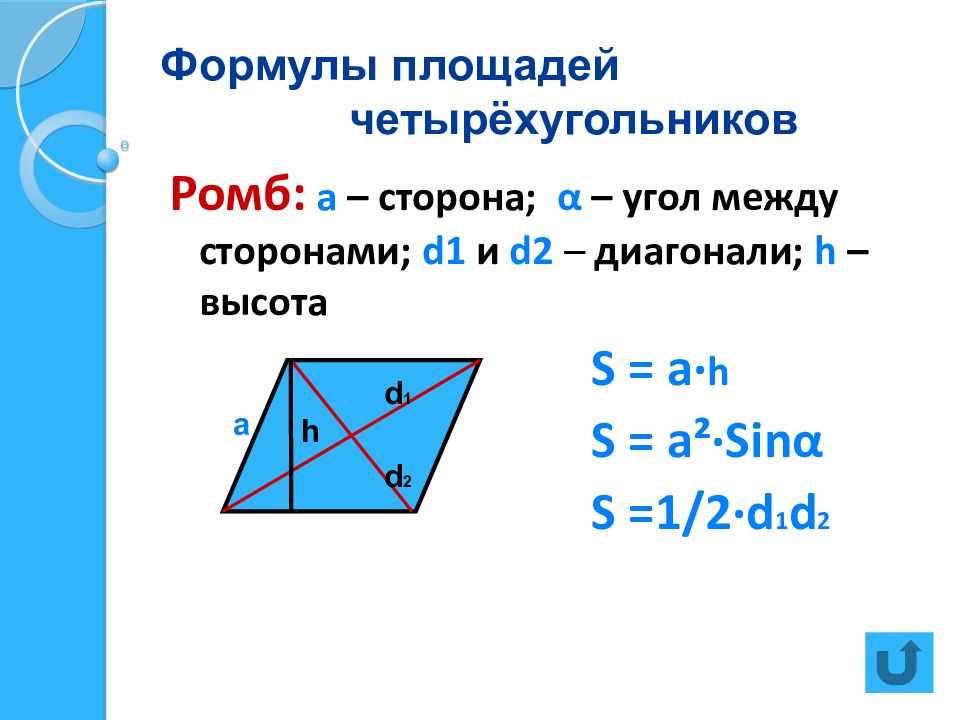
Слайд 19: Формулы площадей четырёхугольников
Ромб: а – сторона; α – угол между сторонами; d1 и d2 – диагонали; h – высота S = a· h S = a²·Sin α S =1 / 2·d 1 d 2 а d 1 d 2 h
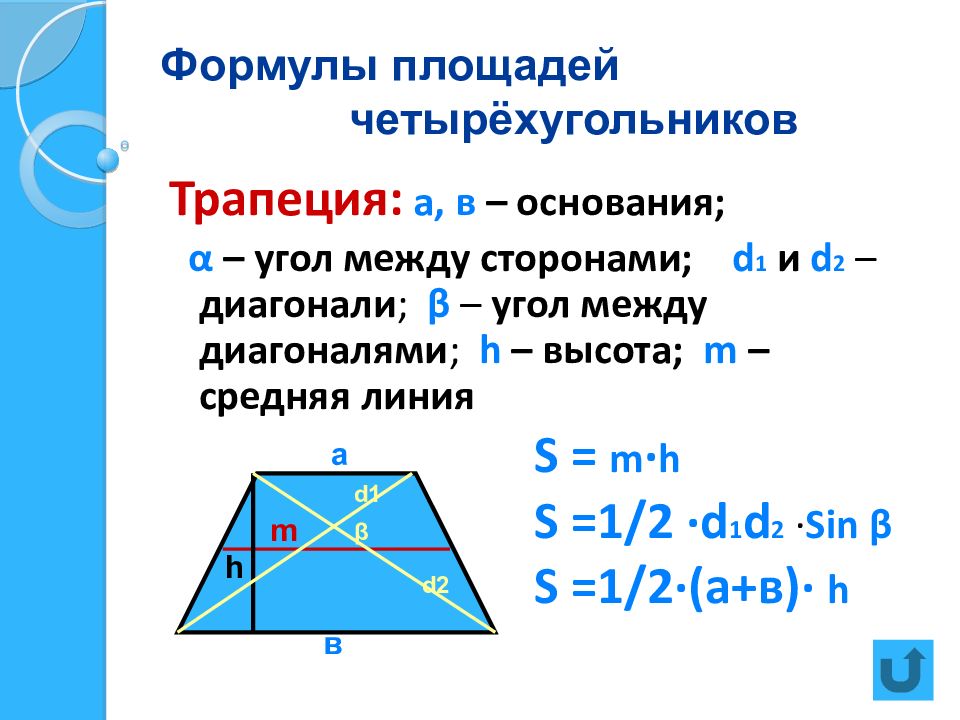
Слайд 20: Формулы площадей четырёхугольников
Трапеция: а, в – основания; α – угол между сторонами; d 1 и d 2 – диагонали ; β – угол между диагоналями ; h – высота; m – средняя линия S = m · h S =1 / 2 ·d 1 d 2 · Sin β S =1 / 2· (а+в) · h в а h m d1 d2 β
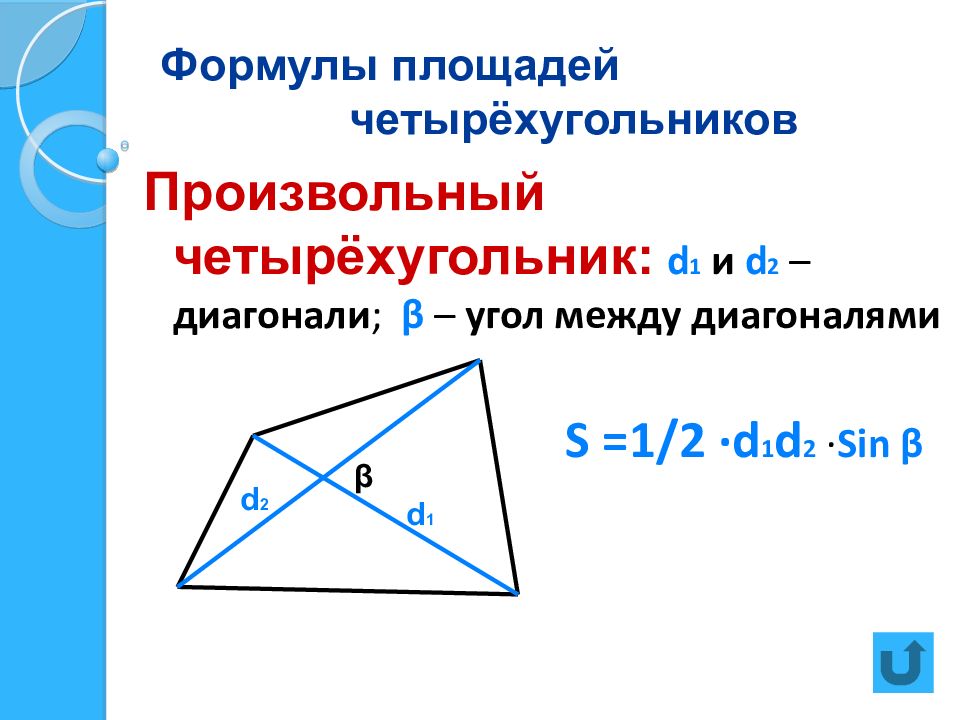
Слайд 22: Формулы площадей четырёхугольников
Произвольный четырёхугольник: d 1 и d 2 – диагонали ; β – угол между диагоналями S =1 / 2 ·d 1 d 2 · Sin β d 1 d 2 β
Последний слайд презентации: Все о четырехугольниках (теория): Используемые ресурсы
Л.С. Атанасян. Учебник геометрии 7-9.М.: «Просвещение», 2009 г. Т.С. Степанова. Математика. Весь школьный курс в таблицах., Минск, «Букмастер»,2012 https://www.google.com/search?hl=ru&site=imghp&tbm=isch&source=hp&biw=1382&bih=732&q=%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0&oq=%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0&gs_l=img.1.0.0l10.11499.13684.0.20805.10.7.0.3.3.0.113.481.6j1.7.0...0.0...1ac.1.7.img.ZRxa7gaF-MI#imgrc=hBP2SMLPpmMX9M%3A%3BLrDnnfsdseyC3M%3Bhttp%253A%252F%252Fimg16.slando.ua%252Fimages_slandocomua%252F74852745_1_644x461_podgotovka-k-zno-matematika-harkov.jpg%3Bhttp%253A%252F%252Fkharkov.kha.slando.ua%252Fobyavlenie%252Fpodgotovka-k-zno-matematika-ID5e1v1.html%3B527%3B461