Первый слайд презентации: Планиметрия
От углов до многоугольников Повторение материала
Слайд 2
Картина Рафаэля «Афинская школа». На ней изображены Пифагор, Евклид, Платон и другие основоположники геометрии, а вокруг них- любознательная молодежь, которой интересны научные открытия.
Научная школа Платона (открыта в 387 г. до н.э. ) – Академия – на протяжении более чем тысячи лет являлась центром культурного классического наследия. Она была размещена на специально купленном для этой цели участке в роще, носившей имя древнеаттического героя Академа Согласно преданию, над дверями Академии Платона было написано «Необученным геометрии вход воспрещён»
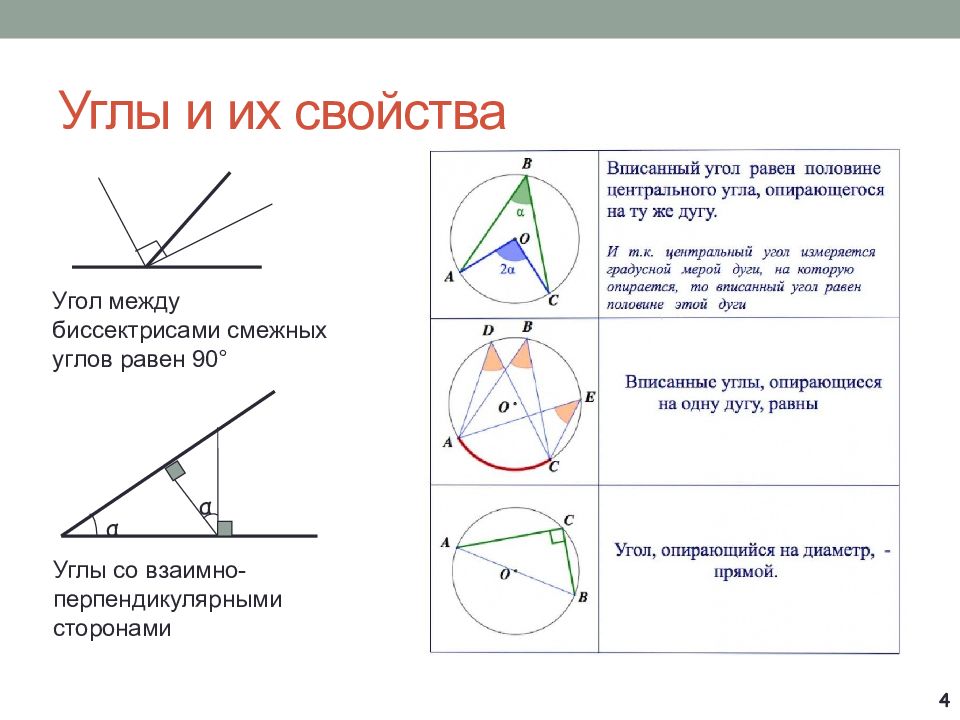
Слайд 4: Углы и их свойства
α α Угол между биссектрисами смежных углов равен 90° Углы со взаимно-перпендикулярными сторонами
Слайд 10: Параллельные прямые
a||b, c - секущая соответственные углы (4 и 5; 6 и 7 ; 1 и 2 ; 3 и 8 ): попарно равны внутренние накрест лежащие углы (2 и 7 ; 3 и 4): попарно равны внешние накрест лежащие углы ( 1 и 6; 5 и 6): попарно равны внутренние односторонние углы (2 и 3 ; 4 и 7): их сумма равна 180° (2 + 3 = 180°; 4 + 7 = 180°) внешние односторонние углы (1 и 8 ; 5 и 6); их сумма равна 180° ( 1 + 7 = 180°; 2 + 8 = 180°) При пересечении двух параллельных прямых третьей прямой, образуются восемь углов, которые попарно называются:
Слайд 11: Треугольники
Первый признак равенства треугольников Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны Второй признак равенства треугольников Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны Третий признак равенства треугольников Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Слайд 12: Треугольники
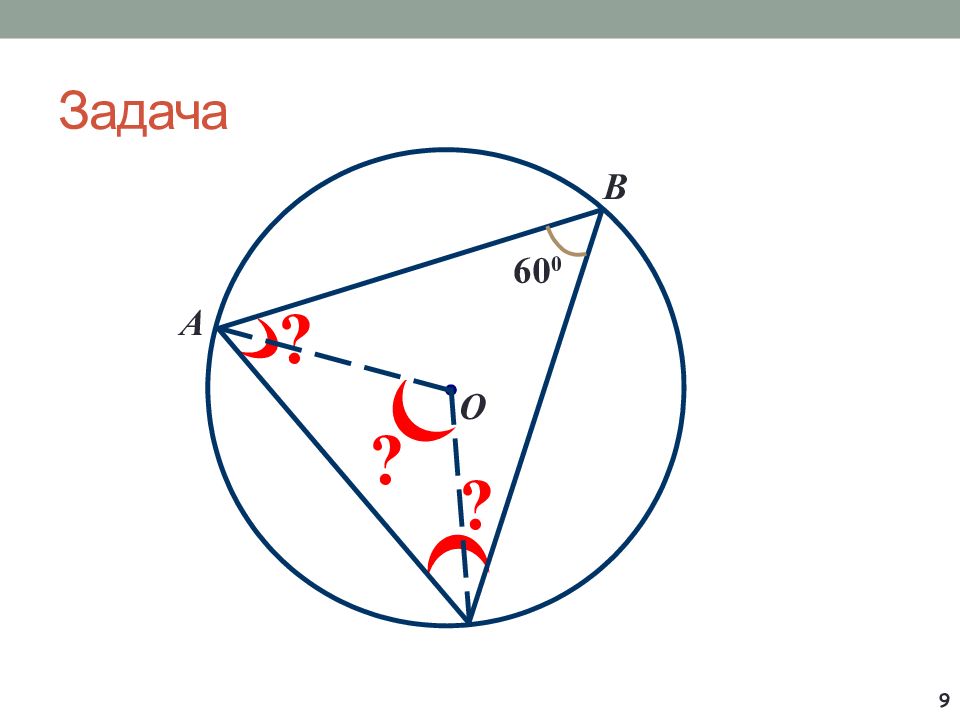
Сумма углов треугольника равна 18 0 ° Неравенство треугольника: Теорема синусов: Теорема косинусов: Центр вписанной окружности равноудалён от всех сторон и является точкой пересечения биссектрис треугольника Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
Слайд 14: Подобие треугольников
I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны II признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны III признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны
Слайд 16: Прямоугольный треугольник
А С B c b a Против угла в 30° лежит катет, равный половине гипотенузы
Слайд 17: Медиана треугольника
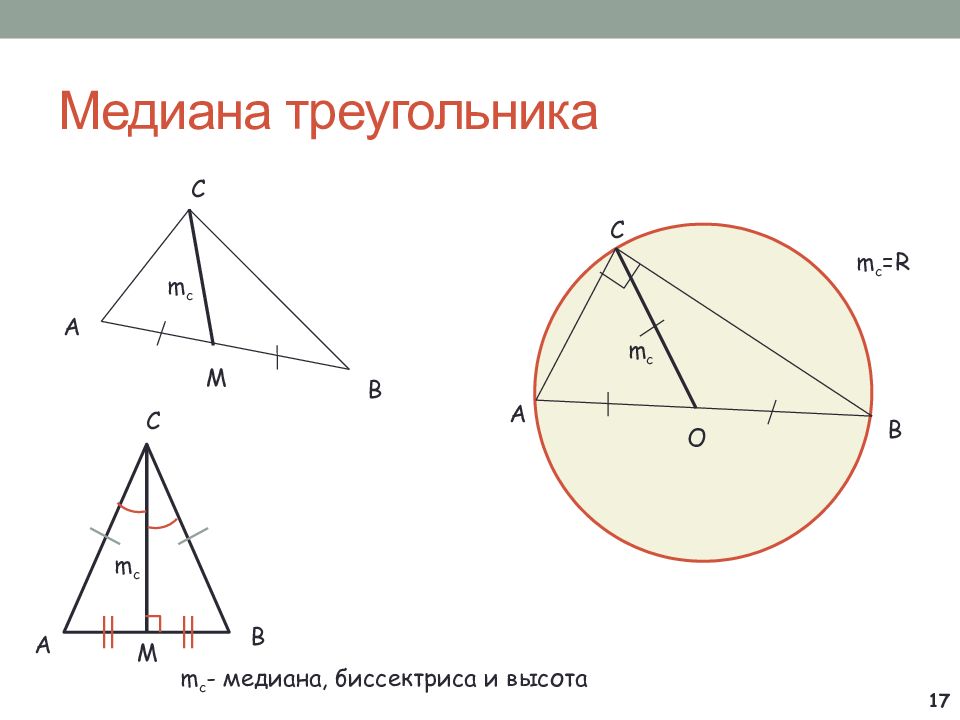
А В С М m c А В С О m c = R m c А С В m c М m c - медиана, биссектриса и высота
Слайд 25: Четырехугольники
невыпуклый выпуклый самопересекающийся Сумма углов четырехугольника равна 36 0 ° Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180° A B C D Выпуклый четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны A B C D
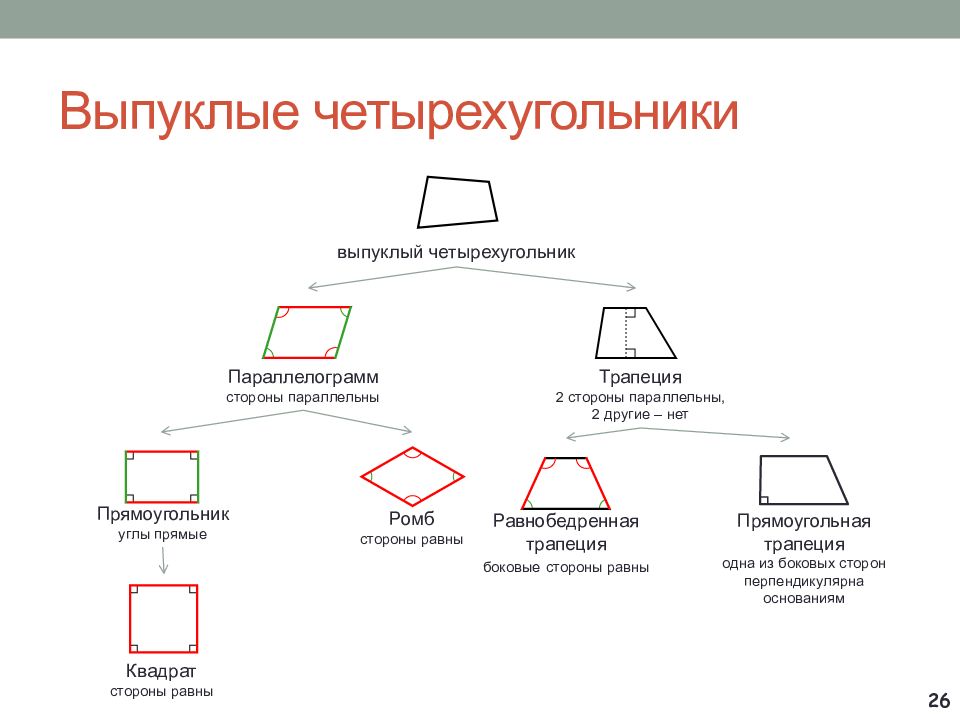
Слайд 26: Выпуклые четырехугольники
выпуклый четырехугольник Параллелограмм стороны параллельны Трапеция 2 с тороны параллельны, 2 другие – нет Прямоугольник углы прямые Ромб стороны равны Квадрат стороны равны Равнобедренная трапеция боковые стороны равны Прямоугольная трапеция одна из боковых сторон перпендикулярна основаниям
Слайд 27: Трапеция
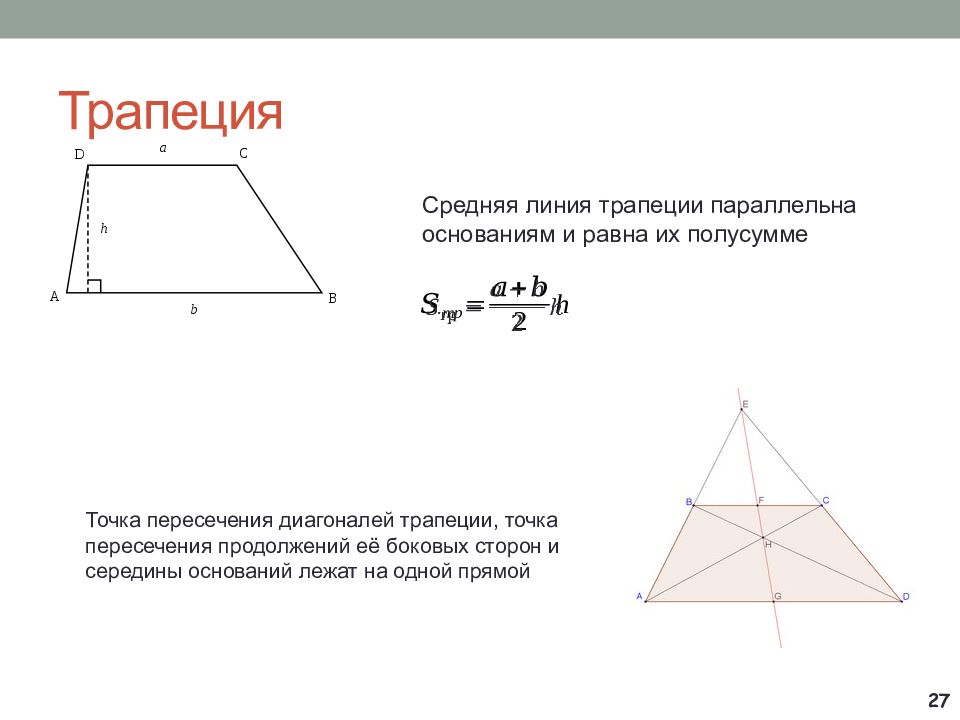
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой Средняя линия трапеции параллельна основаниям и равна их полусумме
Слайд 28: Параллелограмм
Противоположные стороны параллелограмма равны Противоположные углы параллелограмма равны Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам Сумма углов, прилежащих к одной стороне, равна 180°
Слайд 29: Прямоугольник и ромб
Диагонали прямоугольника равны d 2 d 1 Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).