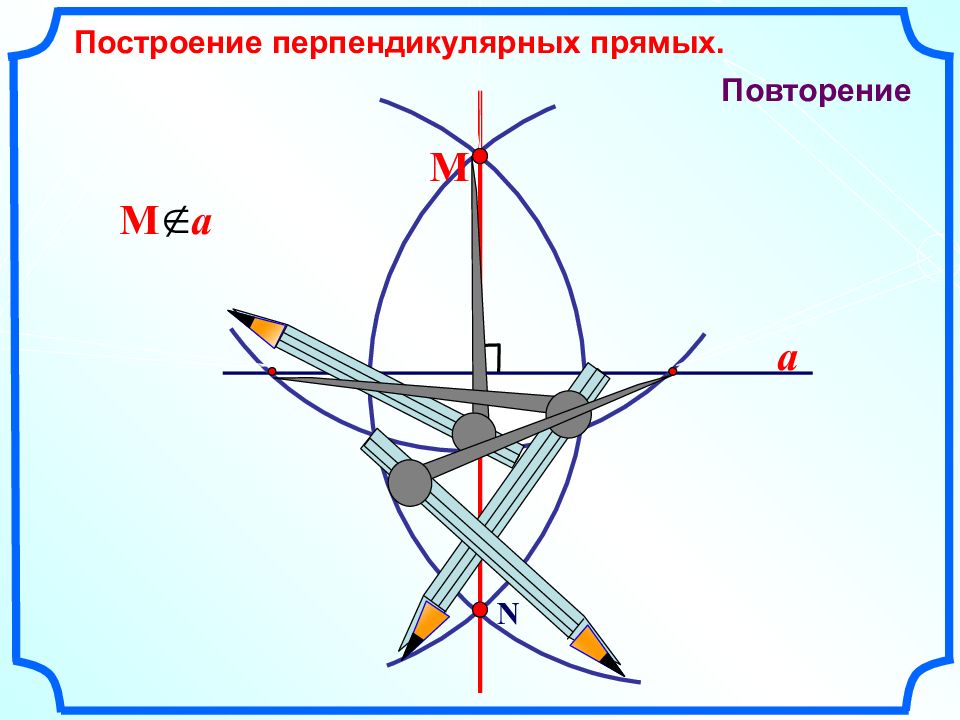
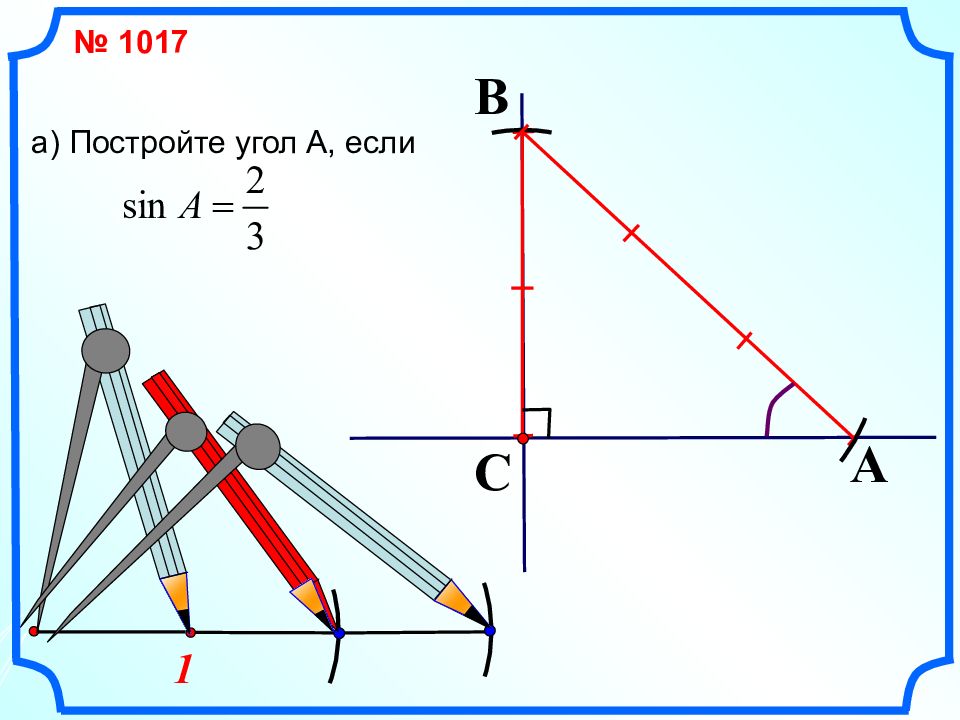
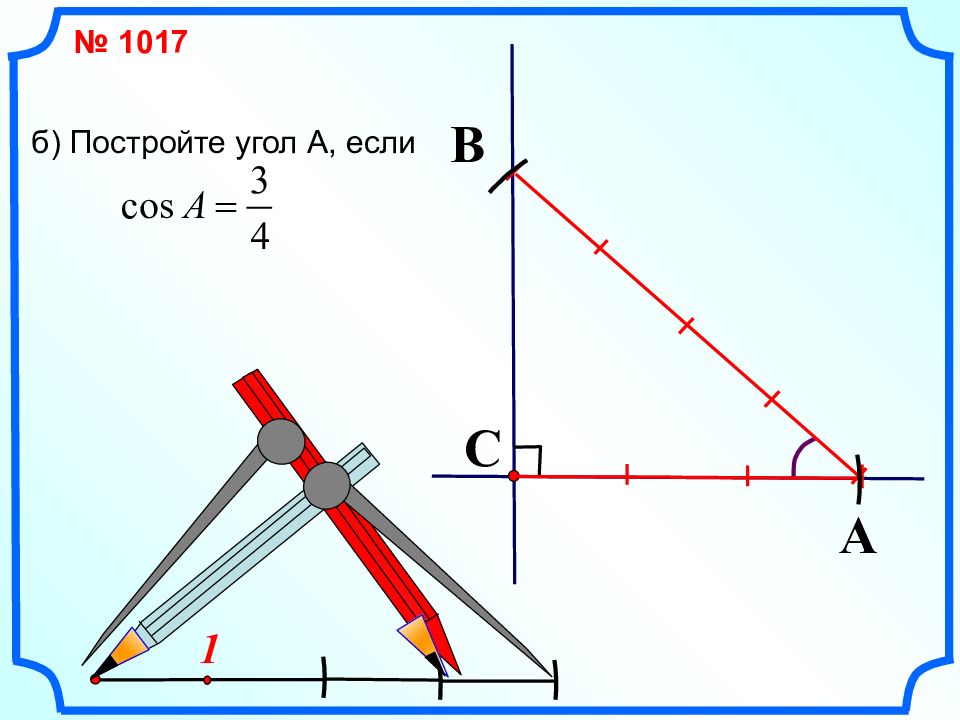
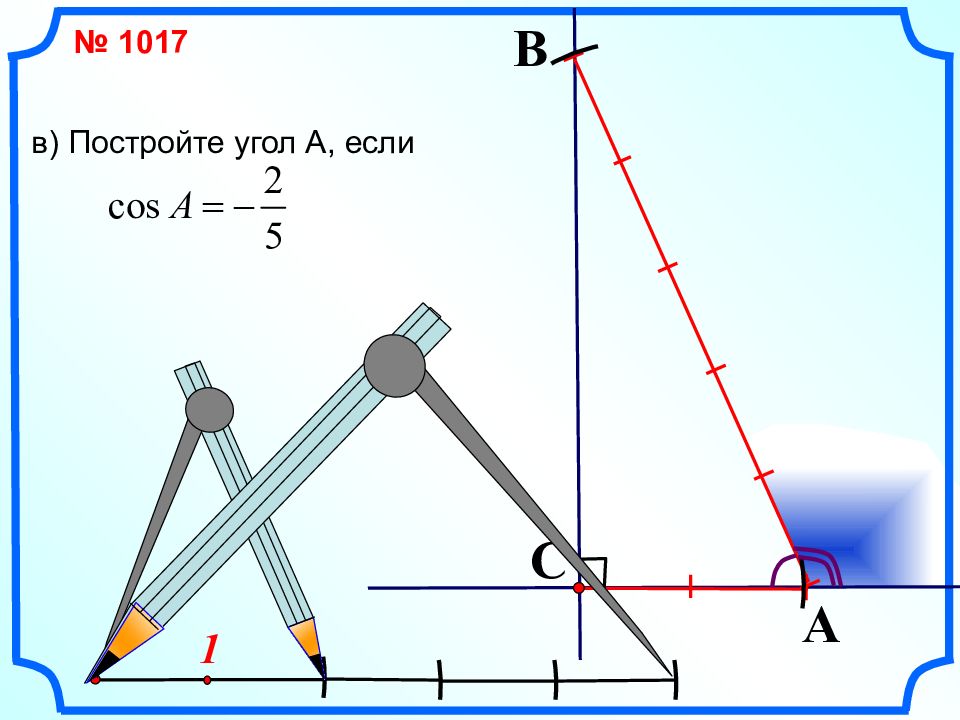
Первый слайд презентации
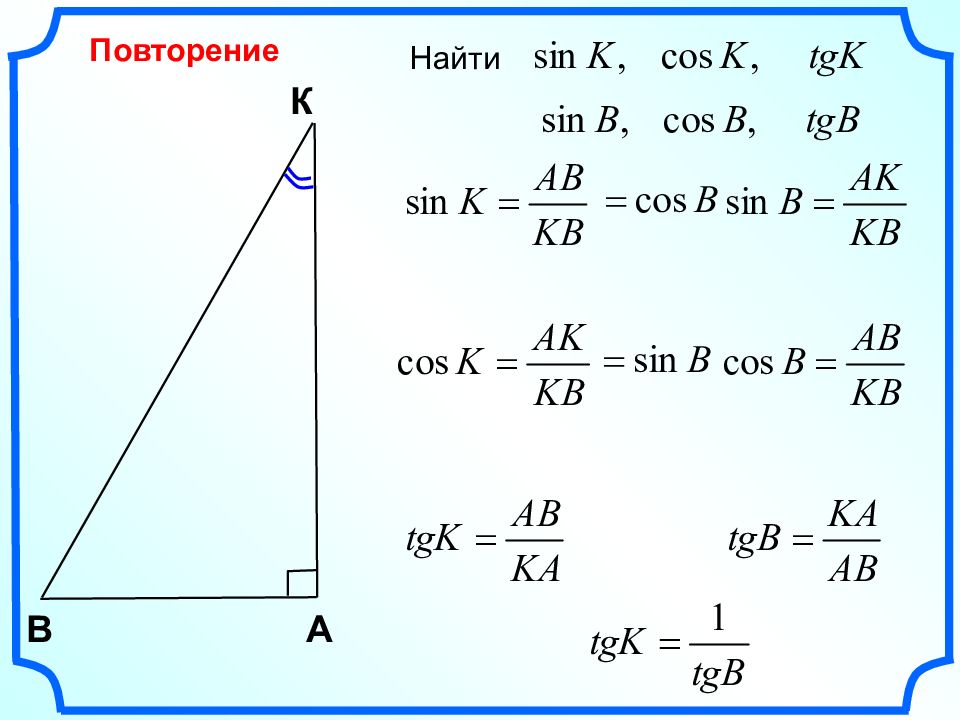
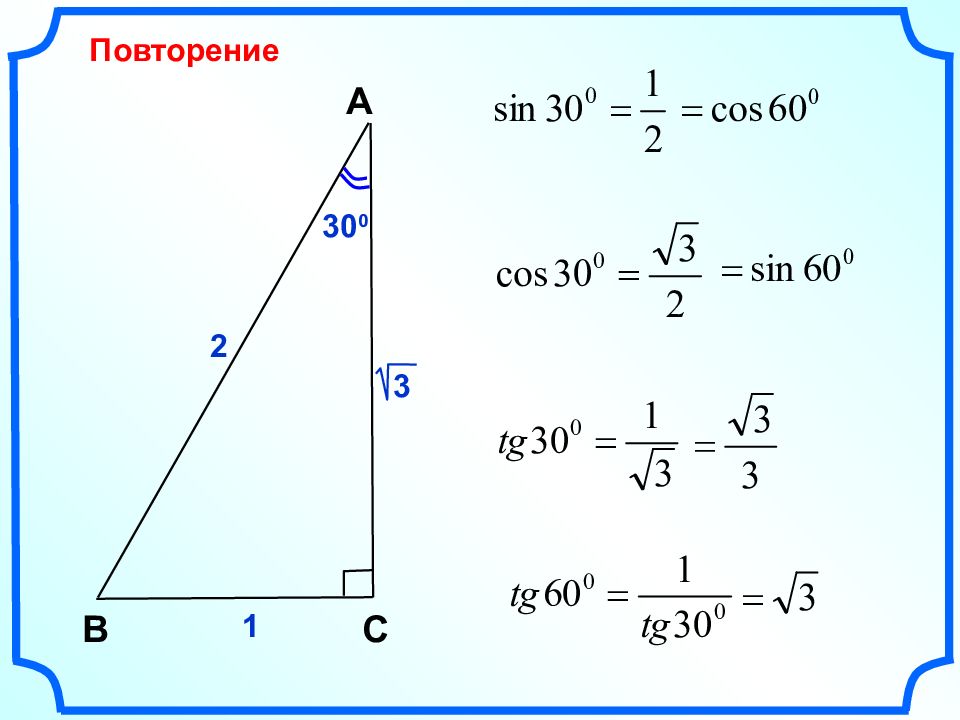
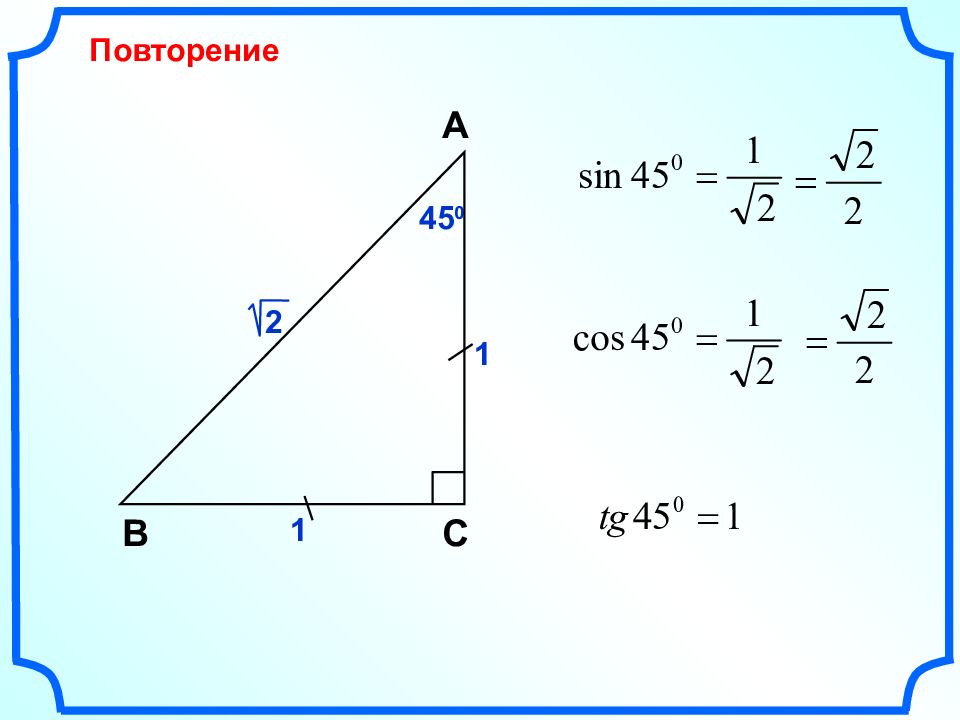
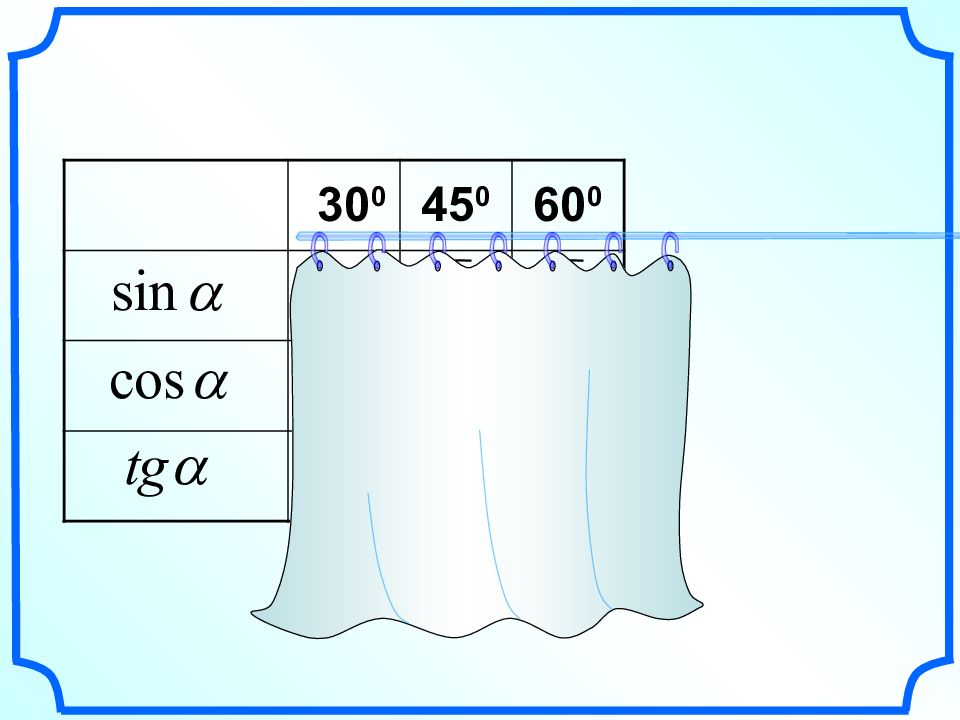
Синус, косинус и тангенс угла Л.С. Атанасян "Геометрия 7-9" Савченко Е.М., учитель математики, МОУ гимназия №, г. Полярные Зори, Мурманской обл.
Слайд 7
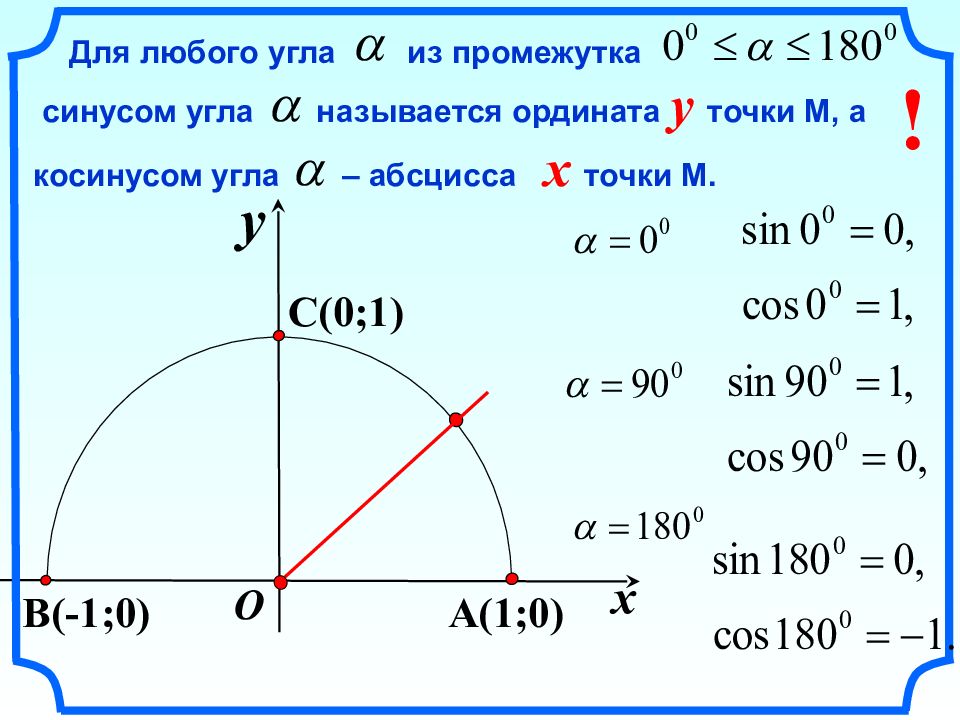
Для любого угла из промежутка синусом угла называется ордината y точки М, а косинусом угла – абсцисса x точки М. x y A ( 1;0) C ( 0;1) O B ( -1;0) !
Слайд 9
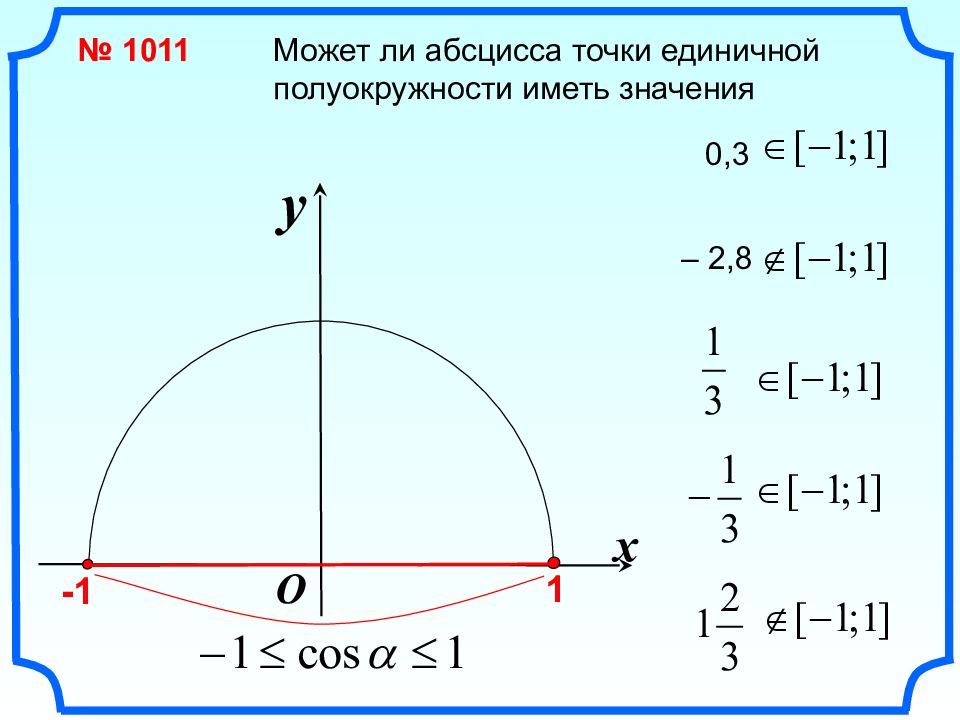
x y O № 1011 -1 1 Может ли абсцисса точки единичной полуокружности иметь значения 0,3 – 2,8
Слайд 10
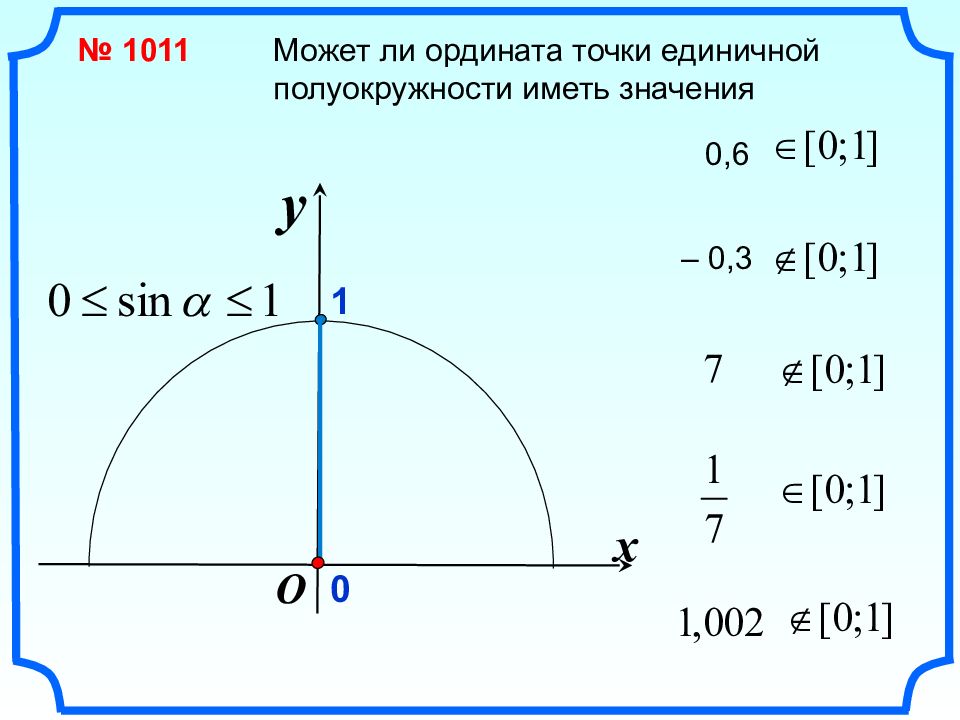
x y O № 1011 0 1 Может ли ордината точки единичной полуокружности иметь значения 0,6 – 0,3
Слайд 11
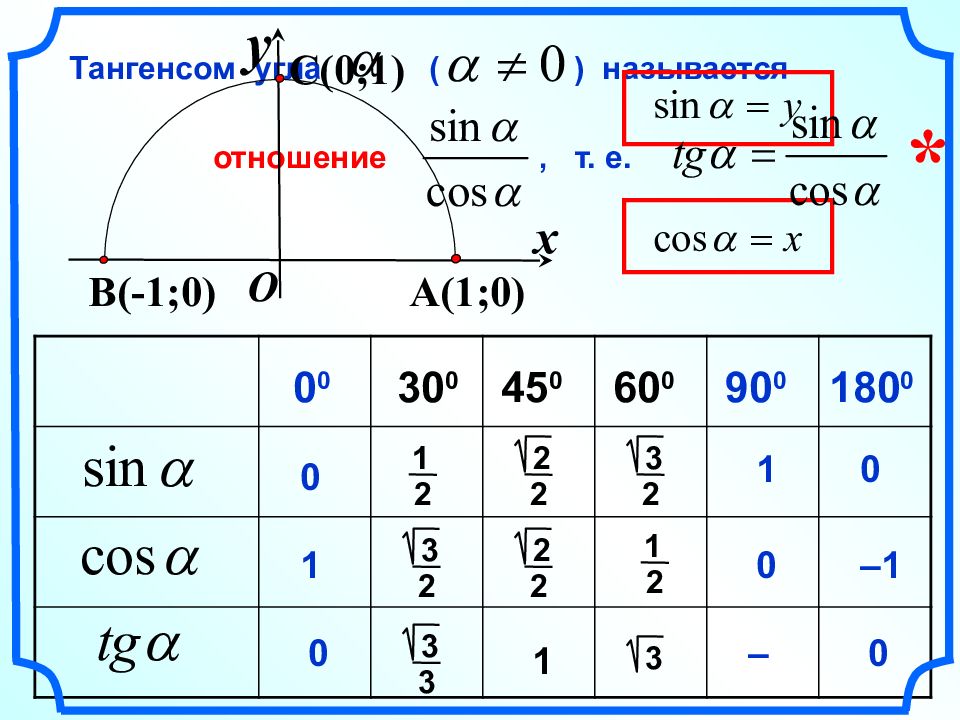
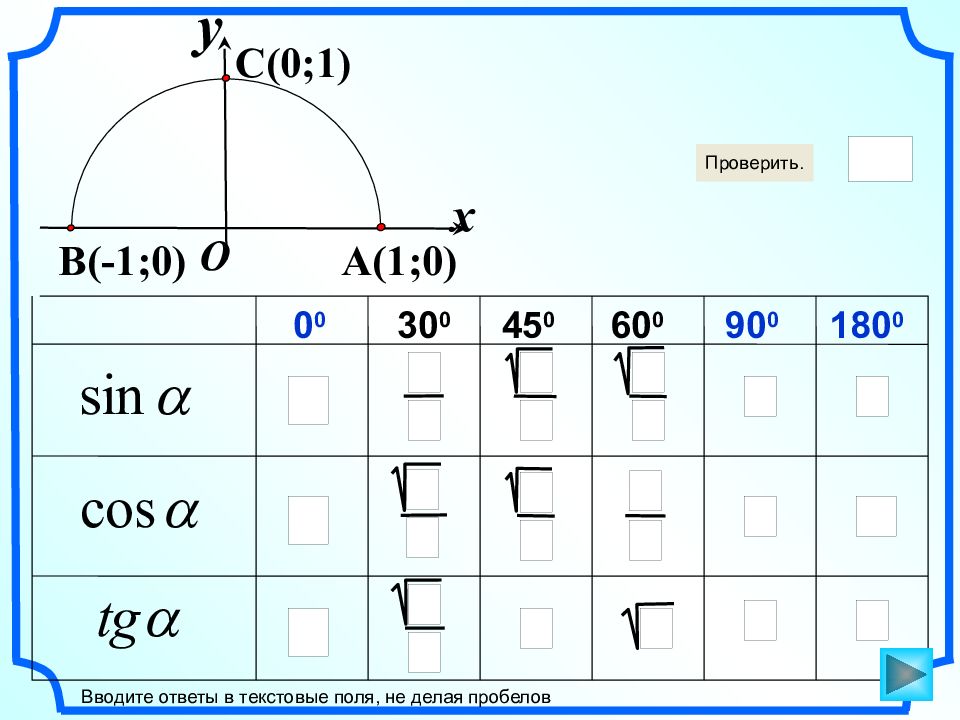
1 2 0 0 30 0 45 0 60 0 90 0 180 0 1 2 3 2 3 2 2 2 2 2 3 3 3 1 0 0 0 0 1 1 –1 0 – Тангенсом угла ( ) называется отношение, т. е. x y A ( 1;0) C ( 0;1) O B ( -1;0) *
Слайд 12
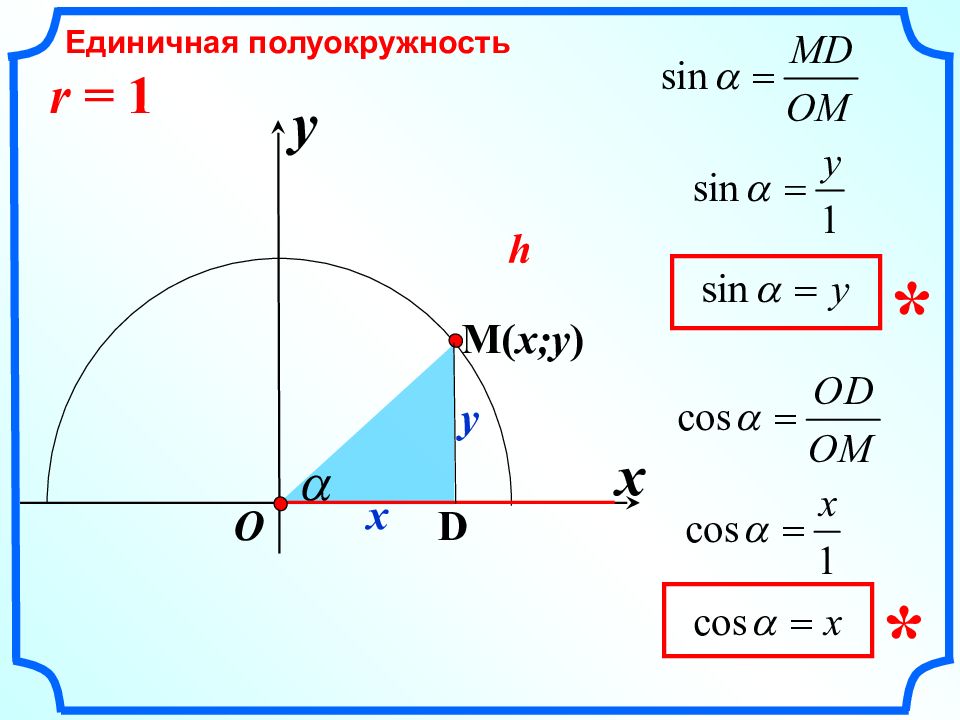
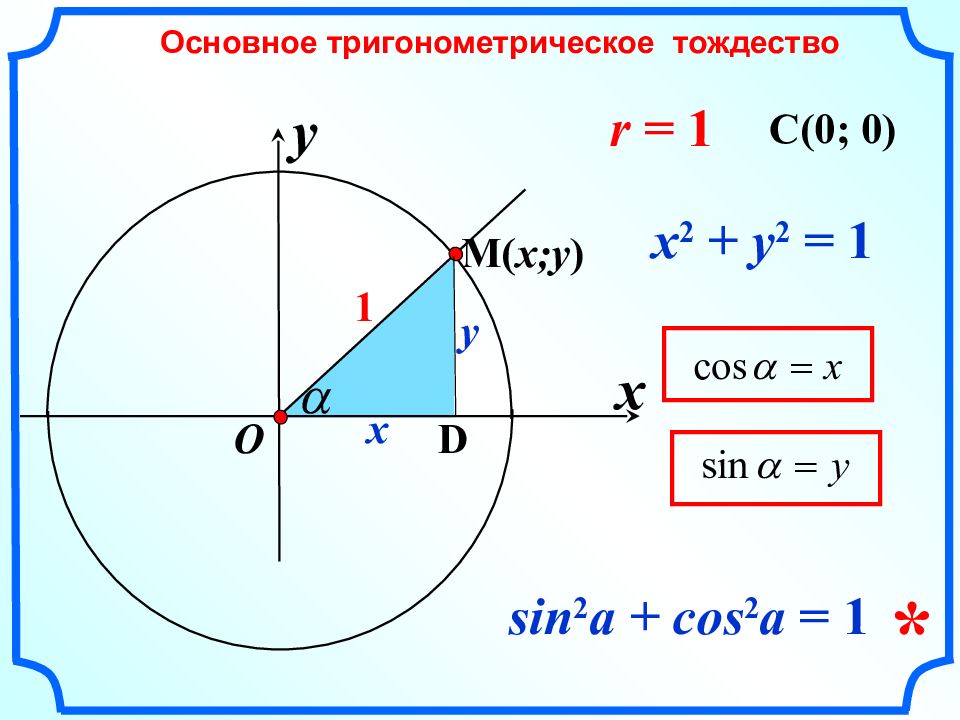
x Основное тригонометрическое тождество y O M ( x;y ) x y D 1 x 2 + y 2 = 1 r = 1 C ( 0; 0) sin 2 a + cos 2 a = 1 *
Слайд 14
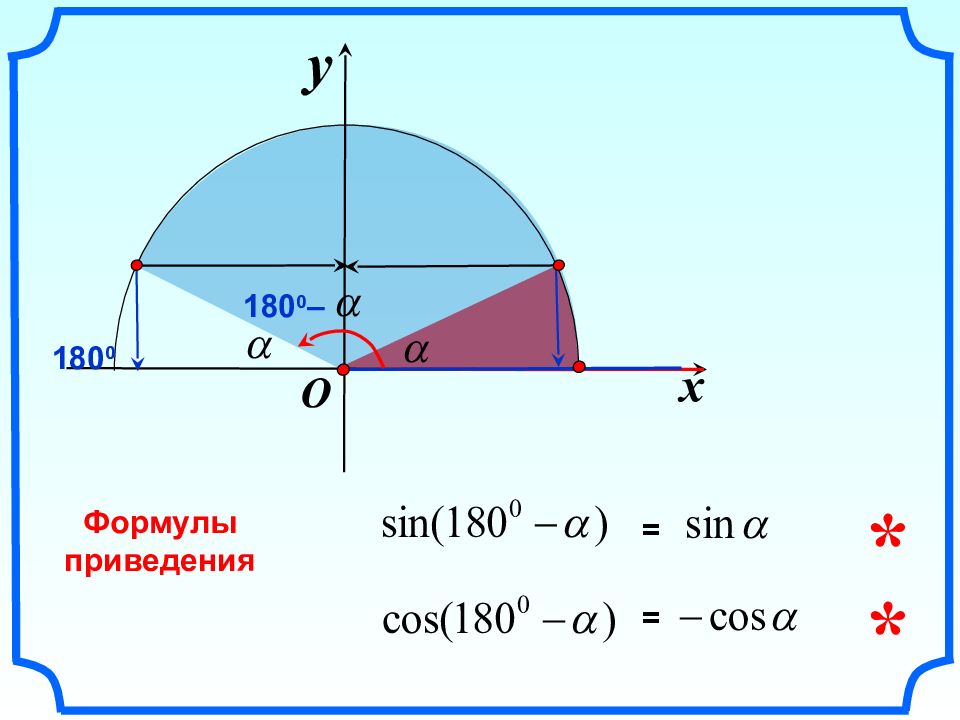
Применение формулы приведения Синус тупого угла равен синусу смежного с ним острого угла. Вычислим быстро! =
Слайд 15
Применение формулы приведения Косинус тупого угла равен «–» косинусу смежного с ним острого угла. Вычислим быстро! =
Слайд 16
60 0 Вводите ответы в текстовые поля, не делая пробелов 0 0 30 0 45 0 90 0 180 0 x y A ( 1;0) C ( 0;1) O B ( -1;0)
Слайд 17
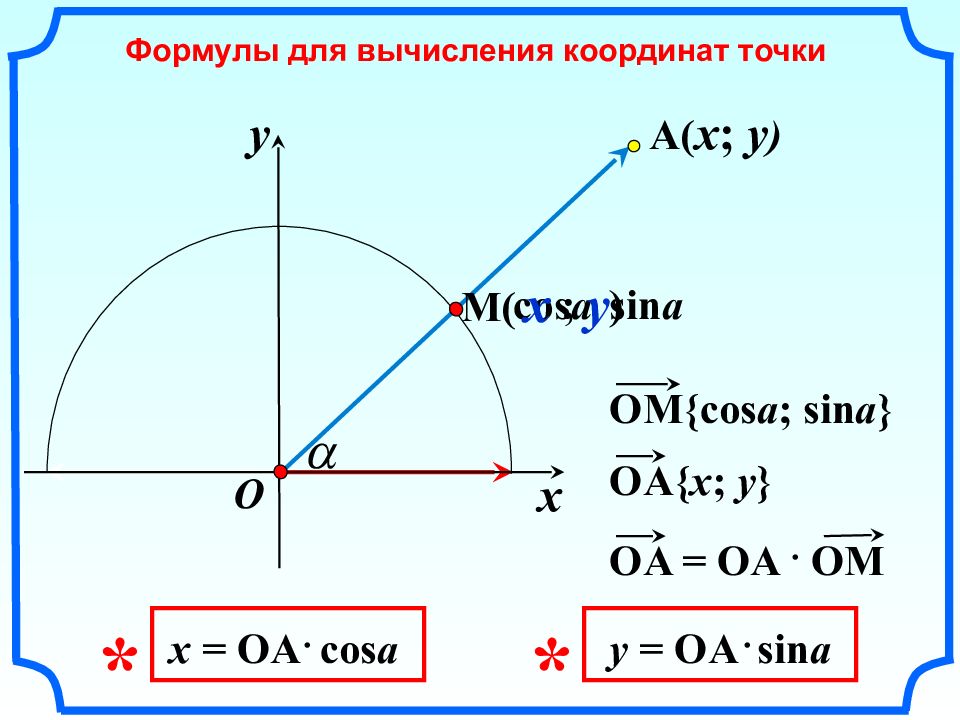
cos a sin a x Формулы для вычисления координат точки y O M ( x y ) ; A ( x ; y ) OM{cos a ; sin a } OA{ x ; y } OA = OA OM x = OA cos a y = OA sin a * *
Слайд 18
x = OA cos a * y = OA sin a * x y O B A = ; 2 3 2 3 Вычислите координаты точек А и В, если ОА=2, ОВ=, ВОС=60 0, ОВ ОА. 3 60 0 OB =, 3 x = cos6 0 0 3 = ( ) 1 2 3 x = 2 cos 1 5 0 0 OA = 2, = 2 (- ) 3 2 = – ; 3 y = 2 sin 1 5 0 0 = 2 2 1 A( - ; 1) 3 y = sin6 0 0 3 2 = ; 3 = 3 2 3 B( ; ) 3 2 2 3 = 1
Слайд 19
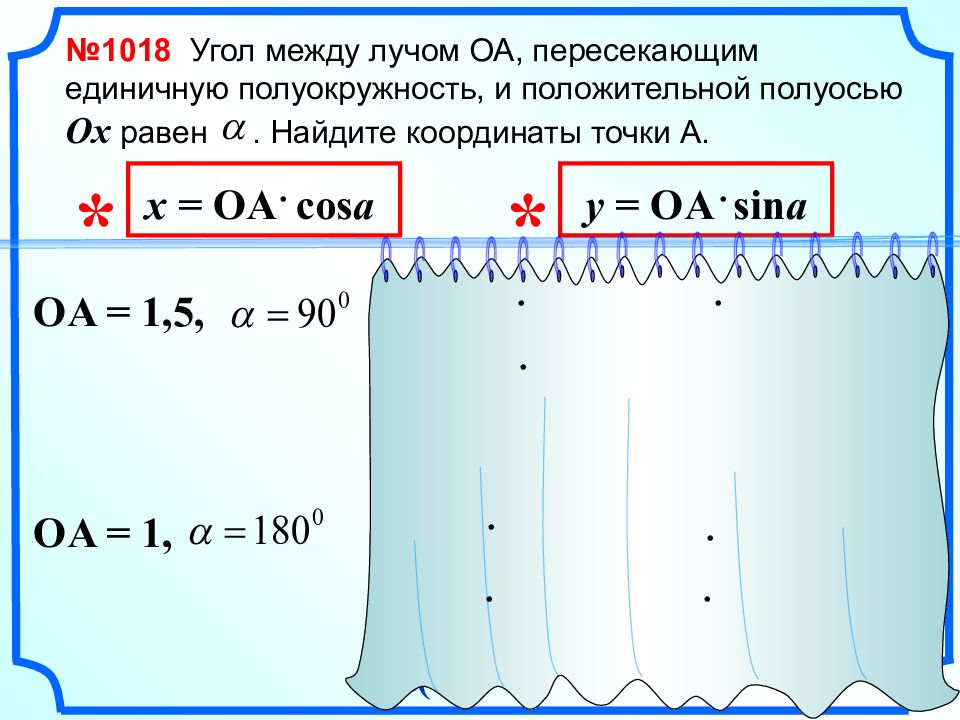
№ 1018 Угол между лучом ОА, пересекающим единичную полуокружность, и положительной полуосью Ox равен. Найдите координаты точки А. x = 3 cos45 0 OA = 3, x = OA cos a y = OA sin a * * = 3 2 2 = ; 3 2 2 y = 3 sin45 0 = 3 2 2 A( ; ) 3 2 2 3 2 2 x = 5 cos 1 5 0 0 OA = 5, = 5 (- ) 3 2 2 = - ; 5 3 y = 5 sin 1 5 0 0 A( - ; ) 5 3 2 2 5 = 5 2 1 x = 2 cos 30 0 OA = 2, = 2 3 2 = ; 3 y = 2 sin 30 0 = 2 2 1 A( ; 1 ) 3
Слайд 20
№ 1018 Угол между лучом ОА, пересекающим единичную полуокружность, и положительной полуосью Ox равен. Найдите координаты точки А. OA = 1,5, x = OA cos a y = OA sin a * * x = 1,5 cos 90 0 = 3 0 = 0 ; y = 1,5 sin 90 0 = 1,5 A( 0; 1,5 ) OA = 1, x = 1 cos 180 0 = 1 (- 1) = -1 A( - 1; 0 ) y = 1 sin 180 0 = 1 0