Г-9, урок № 1 Тригонометрические функции угла от 0° до 180°.
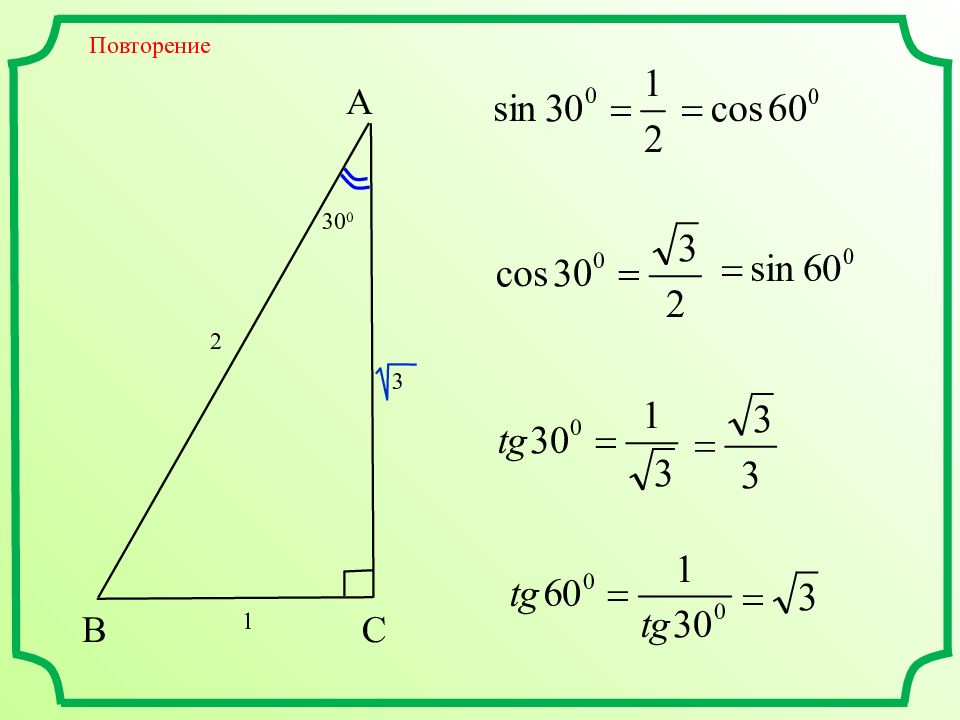
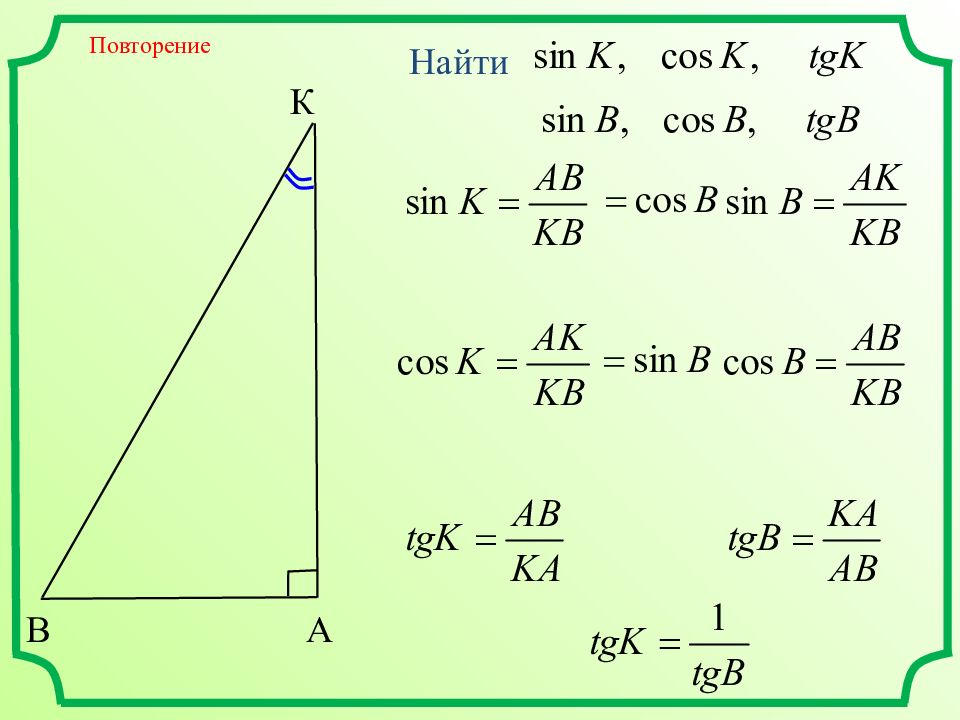
Настройся на урок Что называют синусом острого угла прямоугольного треугольника? А В С Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Настройся на урок Что называют косинусом острого угла прямоугольного треугольника? А В С Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Настройся на урок Что называют тангенсом острого угла прямоугольного треугольника? А В С Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Настройся на урок Что называют котангенсом острого угла прямоугольного треугольника? А В С Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Повторение A C В 30 0 2 1 3
Повторение К A В Найти
1 2 30 0 45 0 60 0 1 2 3 2 3 2 2 2 2 2 3 3 3 1
01.09.2022 Классная работа Тригонометрические функции угла от 0° до 180°.
Сегодня на уроке Научимся оперировать понятиями синуса, косинуса, тангенса и котангенса угла от 0° до 180°, выводить и применять основное тригонометрическое тождество и формулы sin(180° - α ) = sin α и cos (180° - α ) = - cos α.
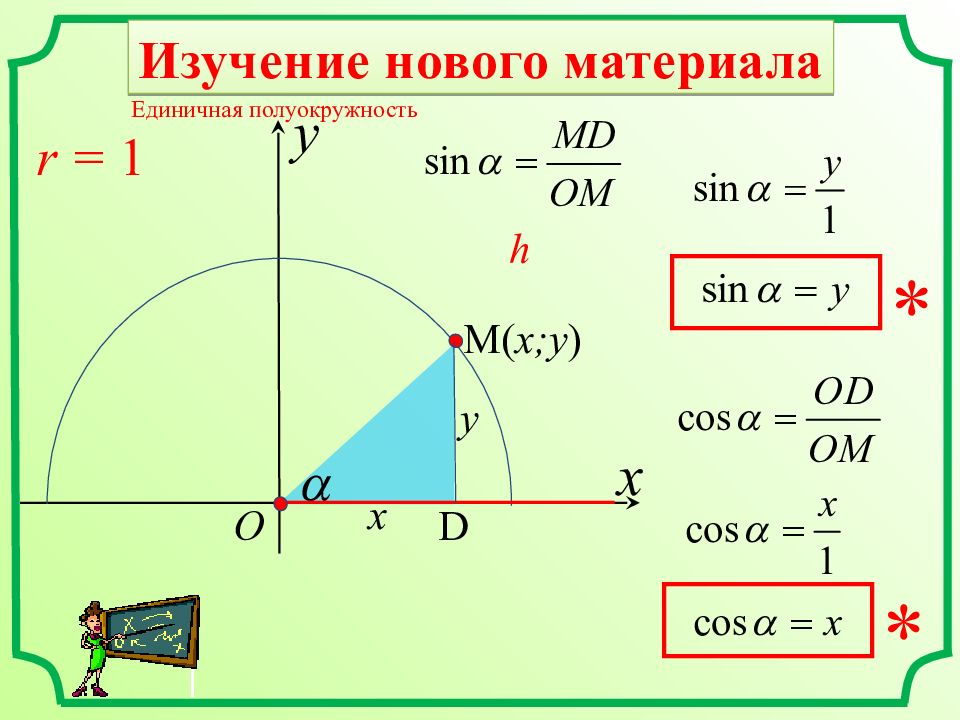
Изучение нового материала x Единичная полуокружность r = 1 y O M ( x;y ) h x y D * *
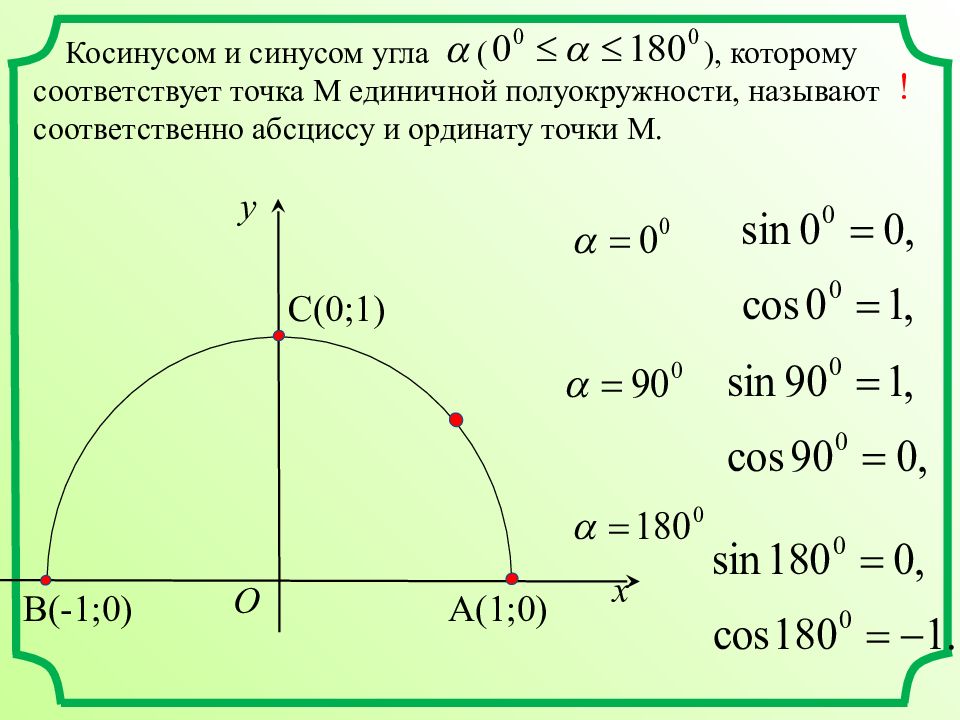
Косинусом и синусом угла ( ), которому соответствует точка М единичной полуокружности, называют соответственно абсциссу и ординату точки М. x y A ( 1;0) C ( 0;1) O B ( -1;0) !
x y O Если угол тупой, то и Если угол острый, то и I II -1 1 0 1 ! !
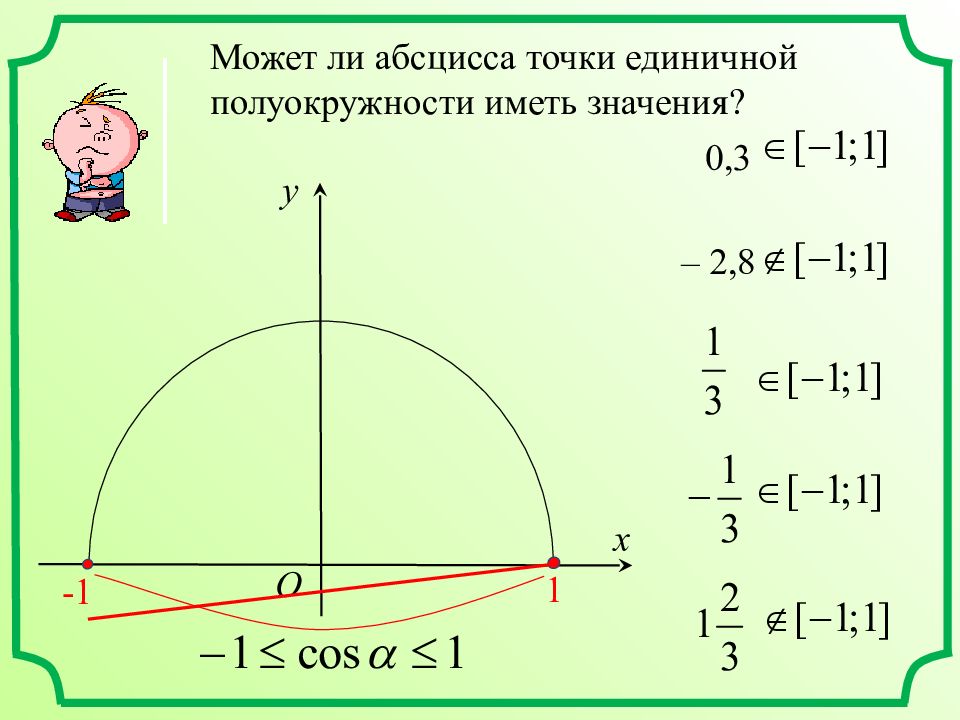
x y O -1 1 Может ли абсцисса точки единичной полуокружности иметь значения? 0,3 – 2,8
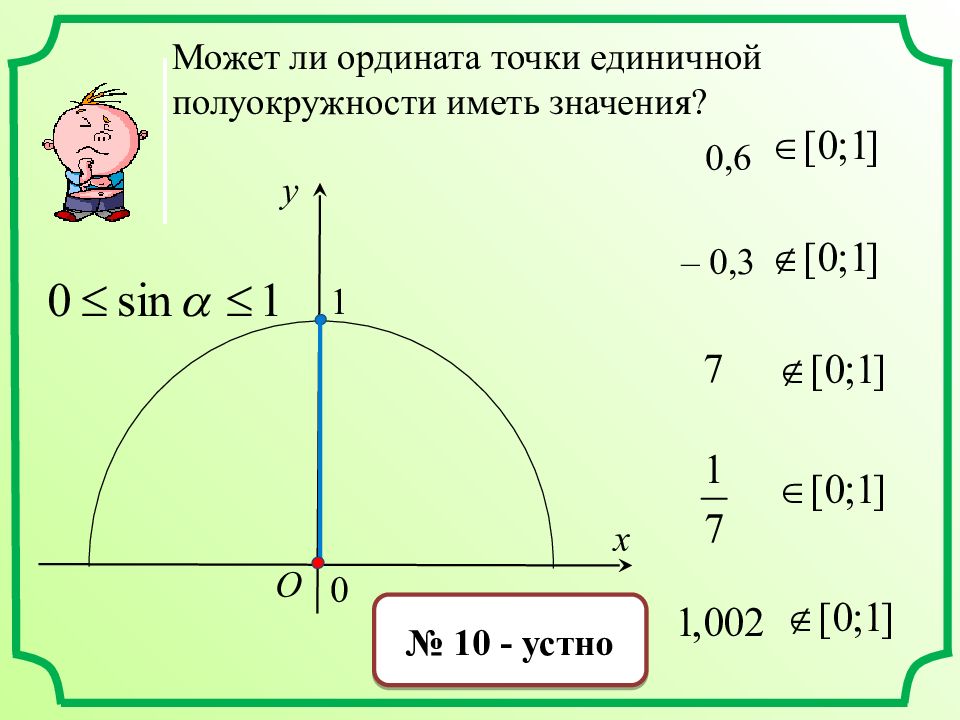
x y O 0 1 Может ли ордината точки единичной полуокружности иметь значения? 0,6 – 0,3 № 10 - устно
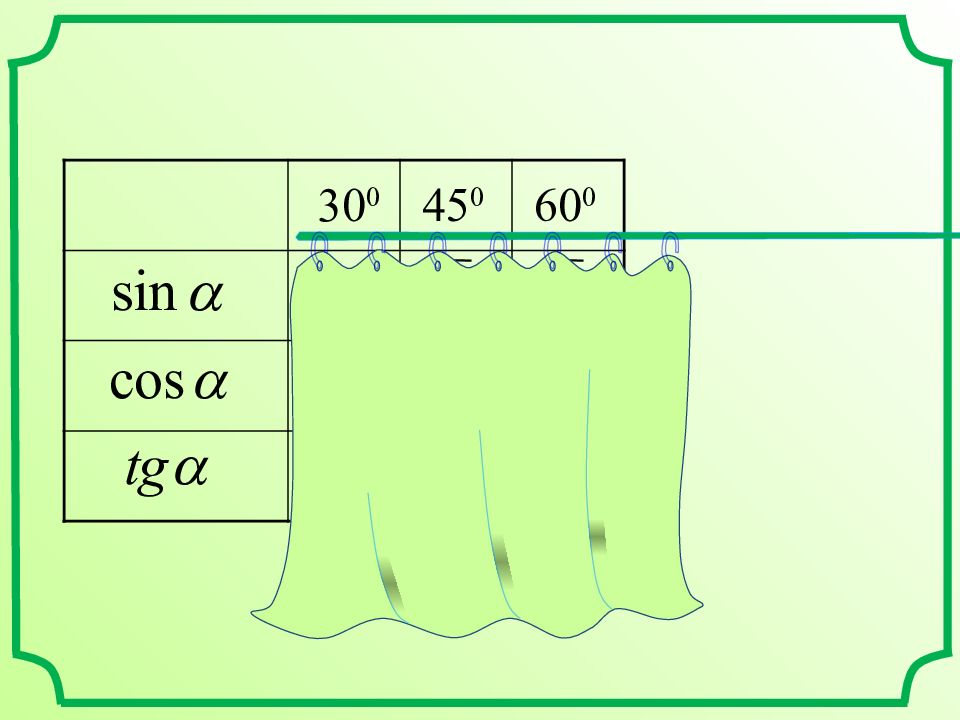
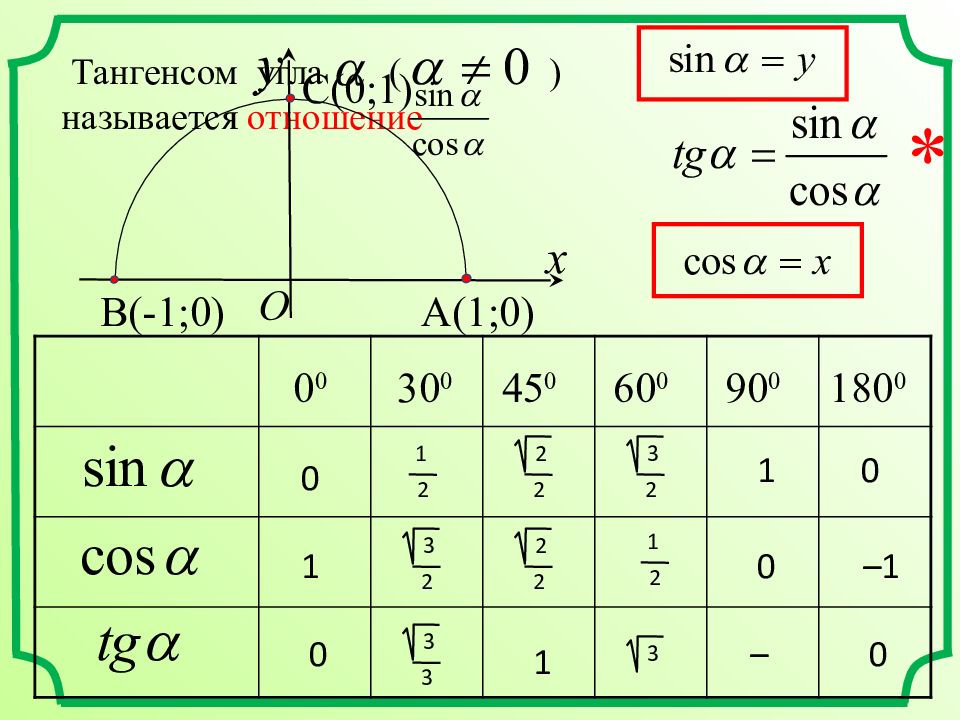
1 2 0 0 30 0 45 0 60 0 90 0 180 0 1 2 3 2 3 2 2 2 2 2 0 0 0 1 1 –1 Тангенсом угла ( ) называется отношение x y A ( 1;0) C ( 0;1) O B ( -1;0) * 0 3 3 1 3 – 0
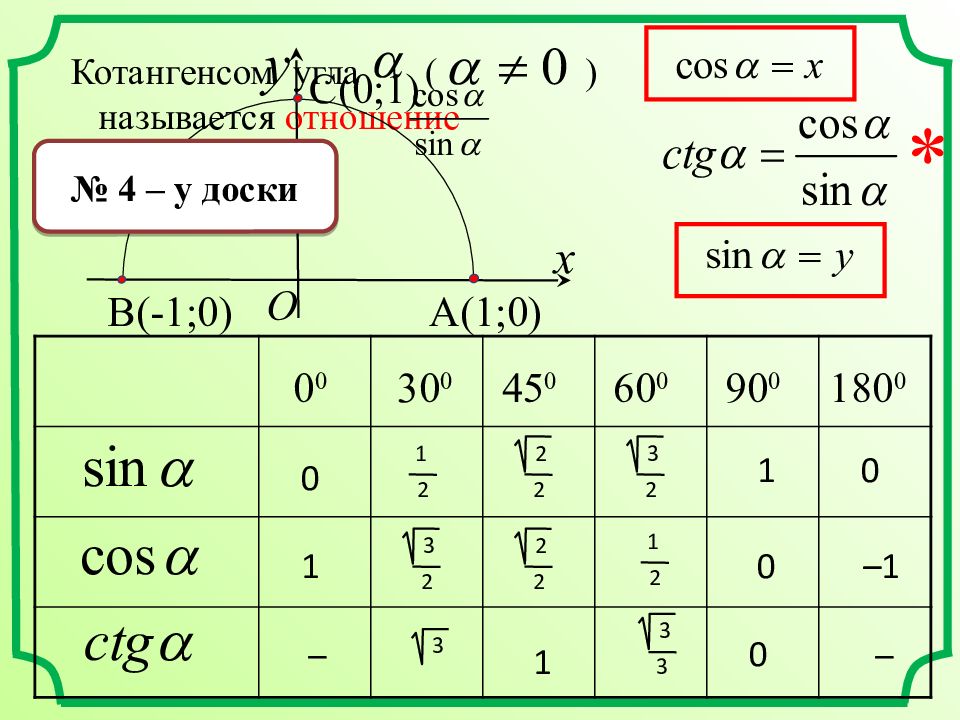
1 2 0 0 30 0 45 0 60 0 90 0 180 0 1 2 3 2 3 2 2 2 2 2 0 0 0 1 1 –1 Котангенсом угла ( ) называется отношение x y A ( 1;0) C ( 0;1) O B ( -1;0) * _ 3 1 3 3 0 _ № 4 – у доски
Домашнее задание Записать и выучить конспект, таблицу
