Первый слайд презентации: Электротехника, электроника и схемотехника
Часть 1. Электротехника. Раздел 6. Переходные процессы Общее представление Виды и параметры ВАХ для нелинейных элементов Методы расчета нелинейных цепей Содержательная часть лабораторной работы 6
Слайд 2: Общее представление
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 2 Общее представление Переходный процесс ( п.п.) – это процесс кратковременного изменения токов и напряжений в электрической цепи в результат ее коммутации или изменения свойств источников электрической энергии или изменениями параметров иных элементов электрической цепи. Обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи. Может сопровождаться перенапряжениями и сверхтоками, разрушающими устройство («быстрые» п.п., обусловленные паразитными реактивными элементами в цепи), но может быть и полезен, например, в генераторах Основные методы расчета: Классический метод, заключающийся в непосредственном интегрировании обыкновенных дифференциальных уравнений, описывающих электромагнитное состояние линейной цепи Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам. Основан на применении преобразования Лапласа и его свойствах. Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого порядка, записанных в нормальной форме (форме Коши) В основе всех перечисленных методов расчета изначально лежат уравнения связи между токами и напряжениями на реактивных элементах U L = L * di / dt и i C = C * dU / dt и уравнения для величины энергии магнитного и электрического полей на этих элементах:
Слайд 3: Основы расчета
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 3 Основы расчета Различают докоммутационные и послекоммутационные начальные значения ( н.з. ), где под коммутацией не обязательно понимать переключение в схемах. Это может быть, например, просто скачкообразное изменение амплитуды питающего цепь синусоидального переменного напряжения. Докоммутационные н.з. – это значения токов и напряжений в цепи непосредственно перед коммутацией (t=0 - ), а послекоммутационные – это их значение в самом начале переходного процесса (t=0 + ). Докоммутационные н.з. могут быть нулевыми и ненулевыми Законы коммутации - Вытекают из закона сохранения электрической энергии и соотношений U L = L * di / dt и i C = C * dU / dt, в которых из физических соображений производная не может принимать бесконечных значений Ток через индуктивность, а в общем случае – потокосцепление I*W для нескольких индуктивностей, или энергия магнитного поля, до и после коммутации одинаковы. Напряжение на емкости, а в общем случае – накопленный на конденсаторах электрический заряд, до и после коммутации одинаковы. Начальные значения на реактивных элементах, определяемые из законов коммутации, будут независимыми, тогда как на остальных элементах цепи – зависимыми, поскольку будут определяться из независимых начальных условий. После завершения переходного процесса при t→∞, снова наступает стационарное состояние. Соответствующие ему токи и напряжения в цепи принято называть принужденными, поскольку они вызваны действием источников энергии. Еще их называют установившимися Свободные токи и напряжения – это абстрактные составляющие токов и напряжений, равные разнице между принужденными значениями и фактически действующими токами и напряжениями в цепи. Обусловлены собственными колебаниями энергии в конденсаторах и индуктивностях цепи, возникающими за счет перехода от одного стационарного состояния цепи к другому. В начале переходного процесса, как правило, их значения максимальны, а в конце – стремятся к нулю. Общий подход к решению: выбор направлений токов в цепи и определение начальных докоммутационных значений. определение начальных послекоммутационных независимых значений для реактивных элементов с помощью основных законов коммутации Дальнейший расчет будет зависеть от выбранного метода (см.предыдущий и следующие слайды)
Слайд 4: Классический метод расчета: основные формулы
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 4 Классический метод расчета: основные формулы Анализ переходного процесса может быть представлен как результат наложения двух режимов: принужденного и свободного. Полное решение линейного дифференциального уравнения с постоянными коэффициентами находят в виде суммы частного решения неоднородного и общего решения соответствующего однородного уравнения: Исходное уравнение по 2-му закону Кирхгофа Итоговое дифференциальное уравнение 2-го порядка Общий вид решения такого уравнения: i св = A 1 ·e p 1 t +A 2 ·e p 2 t Алгебраизация – замена n- х производных по времени на параметр p n Корни находятся из характеристического уравнения p 2 +(R/L)p+(1/LC)=0 и могут быть кратными или комплексно сопряженными, но не могут быть положительными, поскольку при t ∞ i св 0. Постоянные интегрирования A 1, A 2 находят из начальных условий, которые определяют с помощью законов коммутации для t=0 +. Резистор (идеальное активное сопротивление) Катушка индуктивности (идеальная индуктивность) Конденсатор (идеальная емкость) при наличии магнитной связи с катушкой, обтекаемой током i M - В общем случае уравнение, описывающее переходный процесс в цепи с n реактивными элементами, имеет вид
Слайд 5: Алгоритм для классического метода расчета
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 5 Алгоритм для классического метода расчета Алгоритм расчета: Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации являются независимыми начальными условиями. Рассчитать принужденный (установившийся) режим при t→∞: найти выражения для принужденных значений токов и напряжений при t∞ и определить их значения. Можно делать после п.п.7 Используя независимые начальные условия, определить необходимые зависимые начальные условия (токи и/или напряжения на активных сопротивлениях) – Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения (заменив на р n производные n- го порядка ), получить характеристическое уравнение и найти его корни. Записать общие выражения для свободной составляющей искомых напряжений и токов в соответствии с видом корней характеристического уравнения. Обычно это выражения для токов в одной или нескольких ветвей. Переписать величины, полученные в предыдущем пункте, и производные от них для случая t = 0. Найти необходимые значения для свободных составляющих и их производных в t=0 + как разность между начальными условиями и выражениями для принужденных составляющих в t=0 +. Приравняв полученные на предыдущем шаге значения значениям выражений для свободных составляющих и их производных в t=0, найти постоянные интегрирования. Записать законы изменения искомых токов и напряжений, сложив выражения для свободной и принужденной составляющих. Методы нахождения характеристического уравнения Для составления характеристического и нахождения его корней можно использовать следующие методы: Путем непосредственного нахождения из законов Кирхгофа искомых токов и/или напряжений После записи системы из n уравнений для случая нулевых источников (однородная система уравнений вида Σ U i =0 и Σ i i =0 по законам Кирхгофа ) приравниваем нулю ее определитель: Δ =0 Через приравнивания нулю входного сопротивления двухполюсника, в котором j ω заменены на p
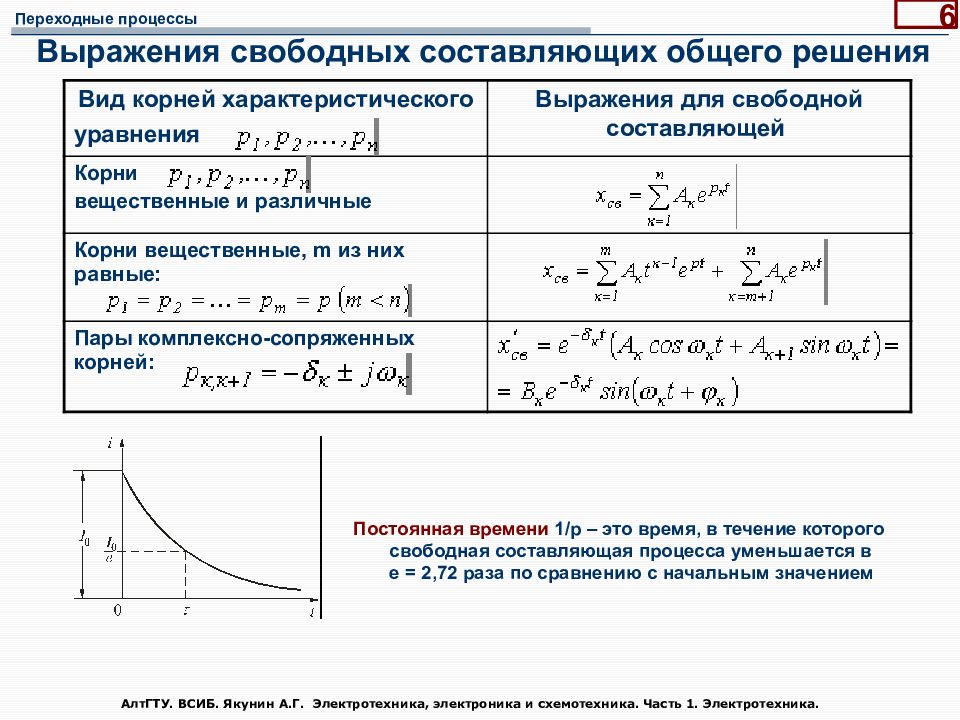
Слайд 6: Выражения свободных составляющих общего решения
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 6 Выражения свободных составляющих общего решения Постоянная времени 1/ p – это время, в течение которого свободная составляющая процесса уменьшается в е = 2,72 раза по сравнению с начальным значением Вид корней характеристического уравнения Выражения для свободной составляющей Корни вещественные и различные Корни вещественные, m из них равные: Пары комплексно-сопряженных корней:
Слайд 7: Примеры классических методов расчета для R-L - цепей
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 7 Примеры классических методов расчета для R-L - цепей 1. Короткое замыкание в цепи с резистором и катушкой Начальное условие: i(0 - ) = i(0 + ) = E / (R вн + R) Установившийся ток (принужденная составляющая) i уст =0 Уравнение для свободной составляющей: Характеристическое уравнение: pL + R = 0, его корень p= - R/L Решение для свободной составляющей: i св = i 0 · e -t/ τ, где τ = -L / R – постоянная времени Из начального условия i 0 = i (0), откуда i = i c в + i уст = E/ ( R вн + R)·e t/ τ 2. Подключение катушки к источнику напряжения Начальное условие: i(0 - ) = i(0 + ) = 0 Установившийся ток (принужденная составляющая) i уст = Е/ R Уравнение для свободной составляющей: Характеристическое уравнение: pL + R = 0, корень p= - R/L=-1/ τ, где τ = -L / R – постоянная времени Решение для свободной составляющей: i св =i 0 · e -t/ τ Из начального условия i (0) =i уст +i св (0) =0 находим, что i 0 = - E/R Тогда i=i c в + i уст = E/R · (1- e -t/ τ )
Слайд 8: Примеры классических методов расчета для R-C - цепей
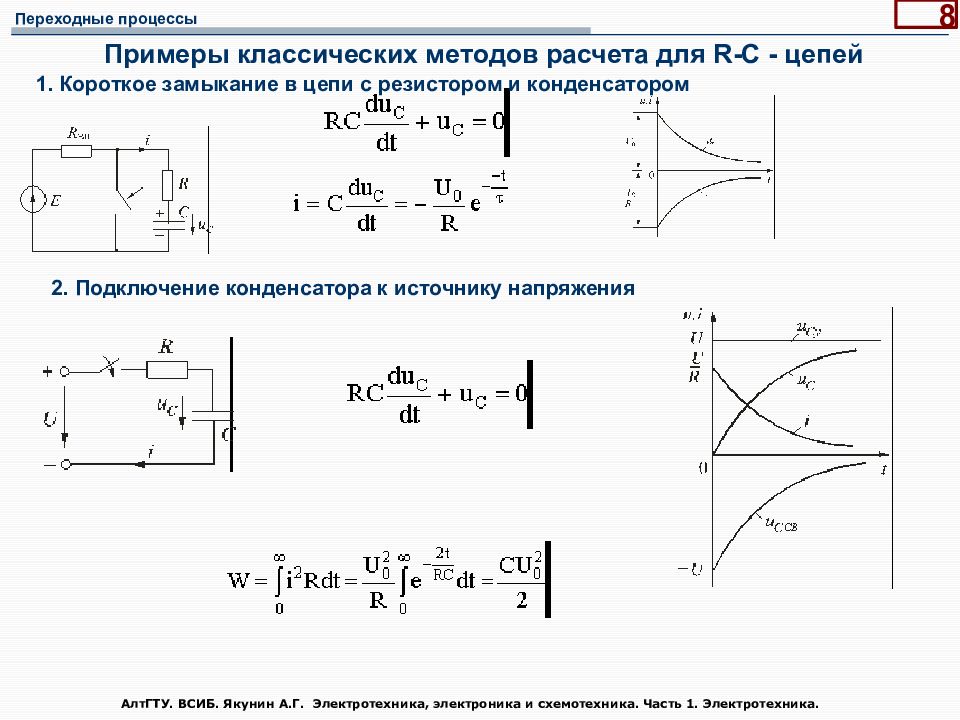
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 8 Примеры классических методов расчета для R-C - цепей 1. Короткое замыкание в цепи с резистором и конденсатором 2. Подключение конденсатора к источнику напряжения
Слайд 9: Примеры классических методов расчета для R-L-C - цепей
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 9 Примеры классических методов расчета для R-L-C - цепей p 1,2 = -α ± jω,
Слайд 10: Подключение R-L-C цепи к источнику напряжения
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 10 Подключение R-L-C цепи к источнику напряжения
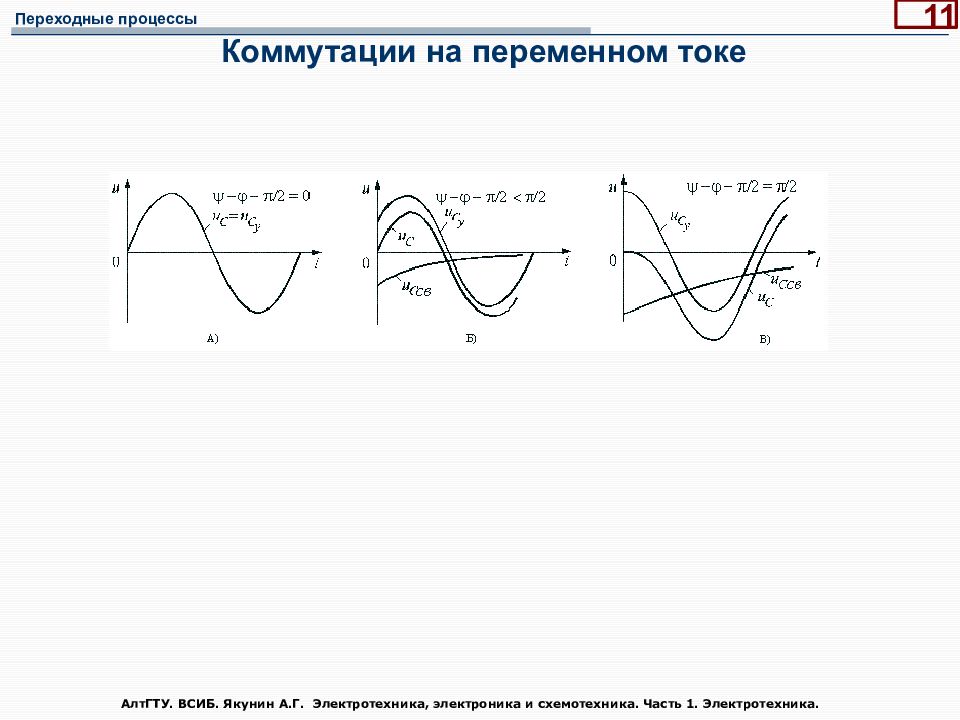
Слайд 11: Коммутации на переменном токе
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 11 Коммутации на переменном токе
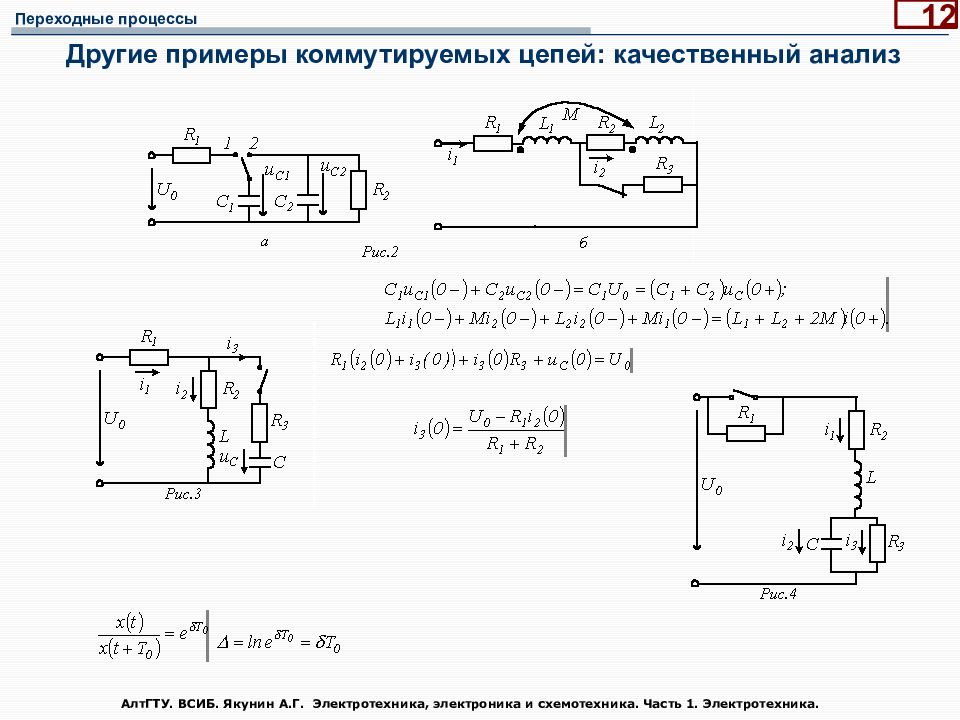
Слайд 12: Другие примеры коммутируемых цепей: качественный анализ
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 12 Другие примеры коммутируемых цепей: качественный анализ
Слайд 13: Операторный метод расчета п.п
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 13 Операторный метод расчета п.п. Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной, которую называют изображением Порядок решения: Заменяем схему с учетом ненулевых независимых начальных условий Находим решение любым из рассмотренных ранее методов для интересуемых участков цепи в виде функции комплексной переменной р. Находим для полученного решения оригинал Прямое преобразование Обратное преобразование Условные обозначения
Слайд 14: Свойства изображений и их виды
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 14 Свойства изображений и их виды Оригинал A Изображение Свойства изображений: Изображение суммы функций равно сумме изображений слагаемых При умножении оригинала на коэффициент на тот же коэффициент умножается изображение: Выражения изображений для производной и интеграла от функции: Другие преобразования: теорема сдвига и теорема о свертке
Слайд 15: Переход от изображений к оригиналам
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 15 Переход от изображений к оригиналам Варианты нахождения оригиналов: Через обратное преобразование по формуле Через таблицы соответствия По формуле разложения путем представления решения в виде суммы простых дробей: Коэффициенты А к находятся по формулам на основе правила Лапиталя Так как - это const, a получим, что Если есть нулевой корень, то
Слайд 16: Расчет п.п.через интеграл Дюамеля
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 16 Расчет п.п.через интеграл Дюамеля П.Д. – пассивный двухполюсник Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости g(t) или (и) переходную функцию по напряжению h(t), можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.
Слайд 17: Магнитные цепи
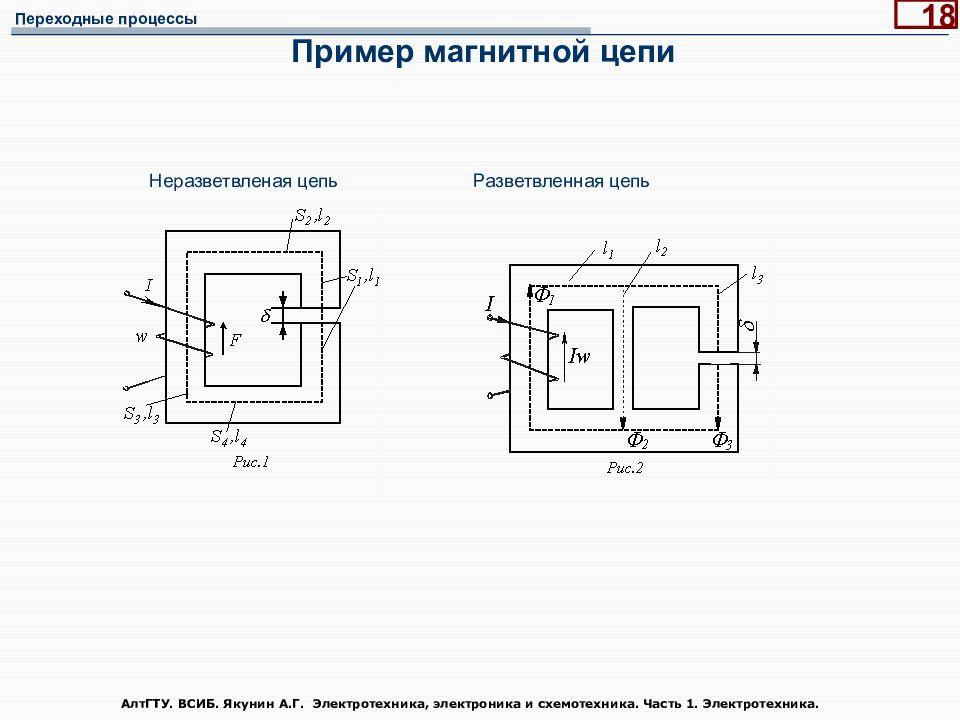
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 17 Магнитные цепи Закон (принцип) непрерывности магнитного потока: поток вектора магнитной индукции через замкнутую поверхность равен нулю Закон полного тока: циркуляция вектора напряженности вдоль произвольного контура равна алгебраической сумме токов, охватываемых этим контуром U= Гн/м, F=A, R м=1/Гн, Ф=Вб, H=A/ м, B= Тл