Пусть на отрезке [ x 0, x n ] определена некоторая функция y = f ( x ), однако полная информация о ней недоступна, либо функция имеет слишком сложное для дальнейшего использования аналитическое описание. Пусть известны значения этой функции в конечном числе точек x 0, x 1,…, x n отрезка [ x 0, x n ]
Слайд 3: Постановка задачи приближения функций:
Требуется по известным значениям y 0 =f( x 0 ), y 1 = f ( x 1 ),…, y n =f( x n ) найти на отрезке [ x 0, x n ] аналитическое выражение для некоторой функции F ( x ), которая приближала бы f ( x ) так, что в известных нам точках : F ( x 0 )= f ( x 0 ) = y 0, F ( x 1 )= f ( x 1 ) = y 1,…, F ( x n )= f ( x n ) = y n.
Слайд 4: Постановка задачи приближения функций:
Такую функцию F ( x ) принято называть интерполирующей, точки x 0, x 1,…, x n - узлами интерполяции.
Слайд 5: Постановка задачи приближения функций:
Подобные задачи интерполяции часто возникают на практике, например, при обработке экспериментальных данных, при работе с табличными функциями, в том случае, если требуется вычислить приближенно значение y = f ( x ) в некоторой точке х *, не совпадающей ни с одной из заданных в таблице.
Слайд 6: Постановка задачи приближения функций:
Если точка х * находится за пределами отрезка интерполирования [ x 0, x n ], то задача определения значения функции в точке x называется экстраполированием.
Слайд 7: Интерполирование функций
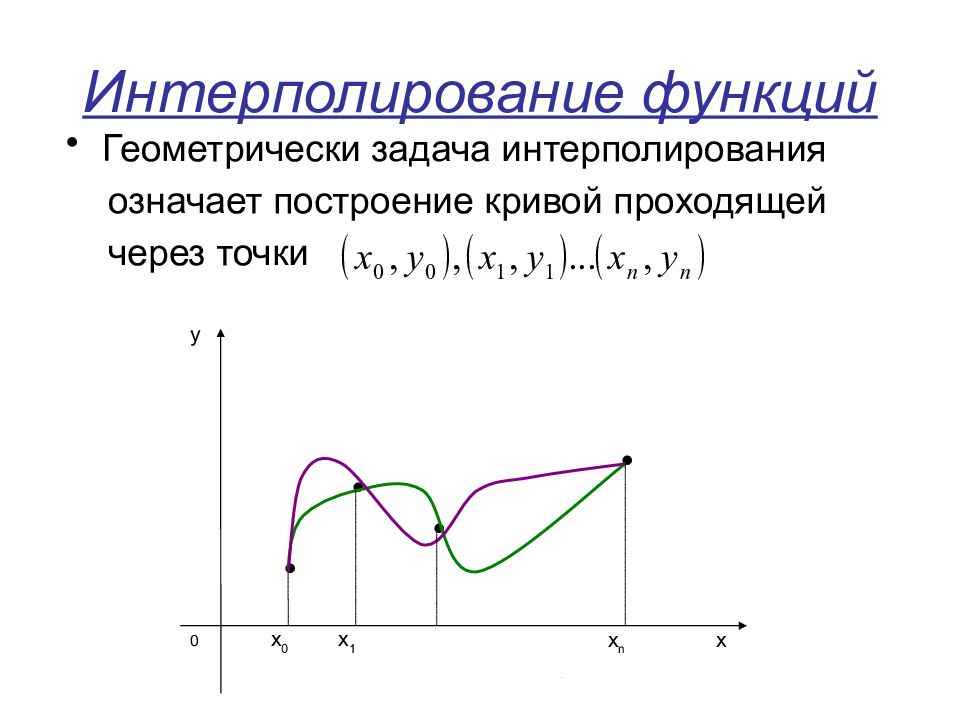
x 1 x n x 0 0 x y Геометрически задача интерполирования означает построение кривой проходящей через точки
Слайд 8: Интерполирование функций
Эта задача будет иметь единственное решение, если в качестве интерполирующей функции F ( x ) для f ( x ), заданной ( n +1) своим значением, выбрать многочлен степени не выше n : P n ( x 0 )=y 0, P n ( x 1 )=y 1,…, P n ( x n )= y n. P n ( x ) при этом называется интерполяци - онным полиномом.
Слайд 9: Задача 1
Построить линейный полином по заданным узлам интерполяции x 0 < x 1 и соответствующим им значениям функции и. Линейная система уравнений для определения a 0 и a 1 имеет вид:
Слайд 10: Задача 1
Определитель этой системы равен . Решив систему, получим: Следовательно:
Слайд 11: Задача 1
Перепишем этот полином в несколько другой форме, выделив и в качестве множителей: Геометрически это прямая на плоскости, проходящая через точки с координатами.
Слайд 12: Интерполяционный многочлен в форме Лагранжа
Требуется построить многочлен такой, чтобы в узлах интерполяции его значения совпадали бы со значениями функции : Задача имеет единственное решение, если степень многочлена не выше n.
Слайд 13: Интерполяционный многочлен в форме Лагранжа
Традиционно интерполяционный полином в форме Лагранжа обозначается Где - неизвестные постоянные коэффициенты, которые нужно найти. В узле интерполяции полином :
Слайд 14: Интерполяционный многочлен в форме Лагранжа
В узле : Наконец в точке : Получаем систему из ( n +1) уравнений с ( n +1) неизвестными:, где и - известные табличные значения аргумента и функции.
Слайд 15: Интерполяционный многочлен в форме Лагранжа
Если определитель системы не равен 0, то она имеет единственное решение. Действительно: , если различны. Любым из известных способов находим
Слайд 16: Интерполяционный многочлен в форме Лагранжа
Перепишем многочлен в другой форме: (1) где
Слайд 17: Интерполяционный многочлен в форме Лагранжа
Легко проверить, что в общем виде функция : В точках функция обращается в 0, а в точке равна 1.
Слайд 18: Интерполяционный многочлен в форме Лагранжа
Для формулы (1) окончательно получим :
Слайд 19: Интерполяционный многочлен в форме Лагранжа
Формулы линейной и квадратичной интерполяции по Лагранжу:
Слайд 20: ПРИМЕР 1
Написать интерполяционный полином второй степени для функции по ее значениям в трех точках: Вычислить с помощью этого полинома приближенное значение синуса в точке , сравнить полученный результат с точным значением синуса и подсчитать погрешность.
Слайд 23: Понятие конечных разностей
Для случая равноотстоящих узлов интерполяции, т.е., где, h - шаг интерполяции, введем понятие конечной разности. Назовём конечной разностью первого порядка разность между значениями функции в соседних узлах интерпо-ляции.
Слайд 24: Понятие конечных разностей
Тогда конечные разности в точках определяются:
Слайд 25: Понятие конечных разностей
В общем виде конечная разность первого порядка: Из конечных разностей первого порядка можно получить конечные разности второго порядка: из второго порядка третьего порядка: и т.д.
Слайд 26: Понятие конечных разностей
В общем виде конечная разность n -го порядка:
Слайд 27: Интерполяционный многочлен в форме Ньютона
Пусть функция f ( x ) задана значениями: в равноотстоящих узлах интерполяции:
Слайд 28: Интерполяционный многочлен в форме Ньютона
Тогда многочлен Лагранжа может быть записан в виде интерполяционного полинома Ньютона: где - конечные разности различных порядков.
Слайд 29: Интерполяционный многочлен в форме Ньютона
Полагая, можно интерполяционный многочлен Ньютона записать в следующем виде:
Слайд 30: Интерполяционный многочлен в форме Ньютона
Итак, в случае равноотстоящих узлов можно воспользоваться интерполяцион-ным полиномом Ньютона. В частности при n=1 имеем формулу линейного интерполирования:
Слайд 31: Интерполяционный многочлен в форме Ньютона
при n =2 - формулу квадратного интерполирования:
Слайд 32: Пример 1
Используя интерполяционный полином Ньютона, вычислить f(0,14), где функция задана таблицей:
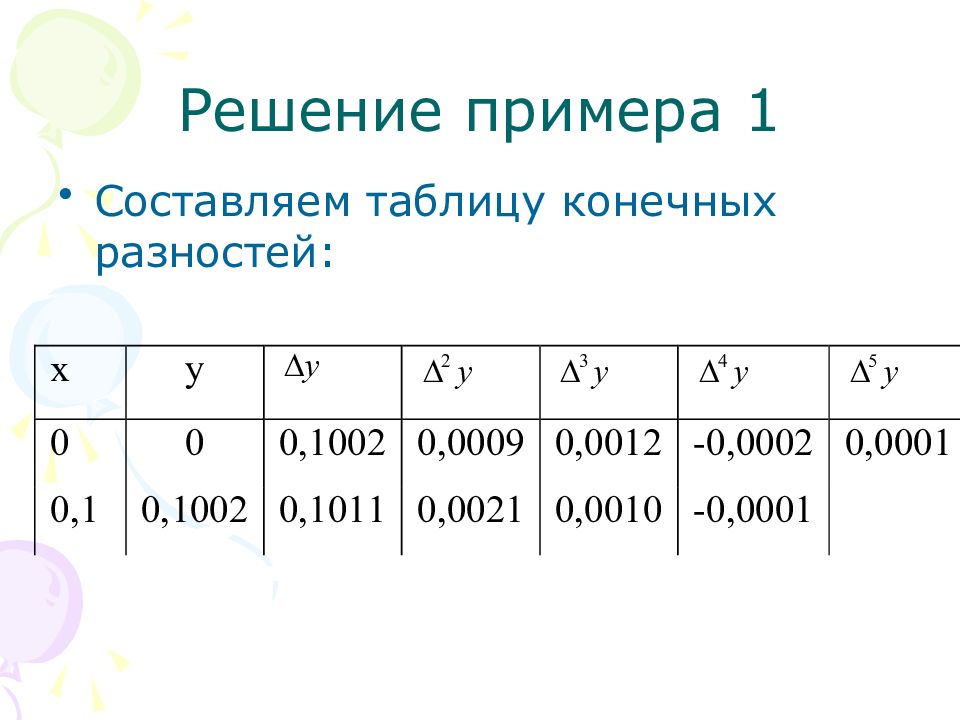
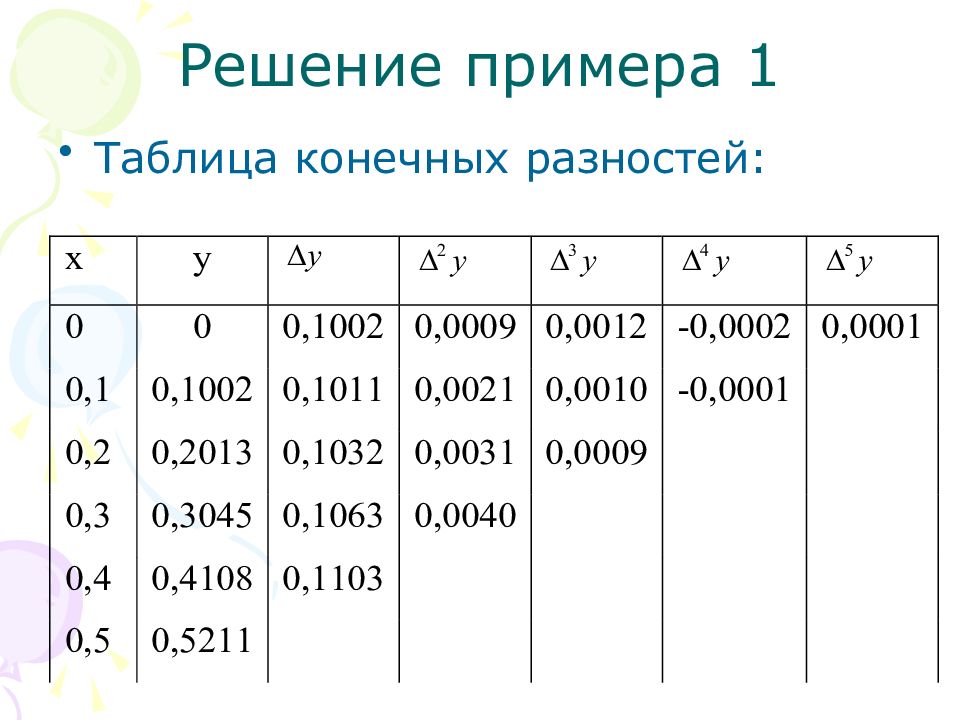
Слайд 35: Решение примера 1
Для вычисления f(0,14) воспользуемся интерполяционным полином Ньютона. Полагаем x 0 =0,1 и h =0,1, тогда и
Слайд 37: РАЗДЕЛЕННЫЕ И КОНЕЧНЫЕ РАЗНОСТИ
В практике интерполирования иногда удобнее использовать многочлены Ньютона, степень которых можно последовательно повышать путем добавления очередных слагаемых, имеющих более высокую степень.
Слайд 38: РАЗДЕЛЕННЫЕ РАЗНОСТИ
Такие несимметричные многочлены, альтернативные симметричным многочленам Лагранжа, основаны на разделенных и конечных разностях, вычисляемых по интерполируемой сеточной функции. Разделенные разности вводятся для функции у = f ( x ), заданной на неравномерной сетке ( h = var )
Слайд 39: Интерполяционный многочлен в форме Ньютона с использованием разделённых разностей
Построим многочлен n - й степени P n ( x ) в форме Ньютона. Этот многочлен имеет вид:
Слайд 40: Интерполяционный многочлен в форме Ньютона
Здесь - разделенные разности 0-го, 1-го, 2-го,:., n -го порядка соответственно. Разделенные разности вычисляются по таблице функции.
Слайд 41: Интерполяционный многочлен в форме Ньютона
Разделенные разности. Величины f ( x 0 ), f ( x 1 ), :, f ( x n ), т.е. значения самой табличной функции в узлах, считаем разделенными разностями нулевого порядка ( k =0). Таким образом, на отрезке [ x 0, x n ] определена n +1 разделенная разность нулевого порядка.
Слайд 42: Интерполяционный многочлен в форме Ньютона
Величина называется разделенной разностью первого порядка ( k =1) на частичном отрезке [ x 0, x 1 ] и вычисляется по уже известным разделенным разностям нулевого порядка на концах отрезка [ x 0, x 1 ] и длине этого отрезка.
Слайд 43: Интерполяционный многочлен в форме Ньютона
Для произвольного частичного отрезка [ x i, x i +1 ] разделенная разность первого порядка ( k =1) равна На отрезке [ x 0, x n ] можно вычислить n разделенных разностей первого порядка, по числу частичных отрезков [ x i, x i +1 ], i =0,..., n -1.
Слайд 44: Интерполяционный многочлен в форме Ньютона
Величина называется разделенной разностью второго порядка ( k =2) на частичном отрезке [ x 0, x 2 ] и и вычисляется по двум найденным ранее разделенным разностям первого порядка.
Слайд 45: Интерполяционный многочлен в форме Ньютона
Для произвольного частичного отрезка [ x i, x i+2 ] разделенная разность второго порядка ( k =2) равна На [ x 0, x n ] можно вычислить ( n -1) разделенную разность второго порядка по числу частичных отрезков [ x i, x i+2 ], поскольку в этом случае 0 i n -2.
Слайд 46: Интерполяционный многочлен в форме Ньютона
Разделенная разность некоторого порядка k на отрезке [ x i, x i+ k ] может быть определена через найденные ранее разделенные разности ( k -1)-го порядка по формуле: На [ x 0, x n ] можно вычислить ( n - k + 1) разделенную разность порядка k, поскольку в этом случае 0 i n - k.
Слайд 47: Интерполяционный многочлен в форме Ньютона
При k = n значение i может быть равно только 0 и мы получаем единственную разделенную разность n -го порядка на всем отрезке интерполирования [ x 0, x n ] по формуле:
Слайд 48: Интерполяционный многочлен в форме Ньютона
Разделенные разности в формуле для многочлена Ньютона P n ( x ) определены, соответственно, для отрезков [ x 0, x 0+ k ], где k =1,..., n.
Слайд 49: Интерполяционный многочлен в форме Ньютона
Теорема : Многочлен P n ( x ), построенный по формуле Ньютона, является интерполяционным многочленом, т.е. в узловых точках значение многочлена равно значению табличной функции: P n ( x i ) = f ( x i )= y i для всех i =0,..., n. Доказывается непосредственной подстановкой точек x 0, x 1,…, x n в формулу Ньютона.
Слайд 50: Интерполяционный многочлен в форме Ньютона
Интерполяционный многочлен степени не выше n, построенный по n +1 узлу интерполяции, единственен. Формула Лагранжа и формула Ньютона предлагают различные способы построения этого единственного многочлена.
Слайд 51: Интерполяционный многочлен в форме Ньютона
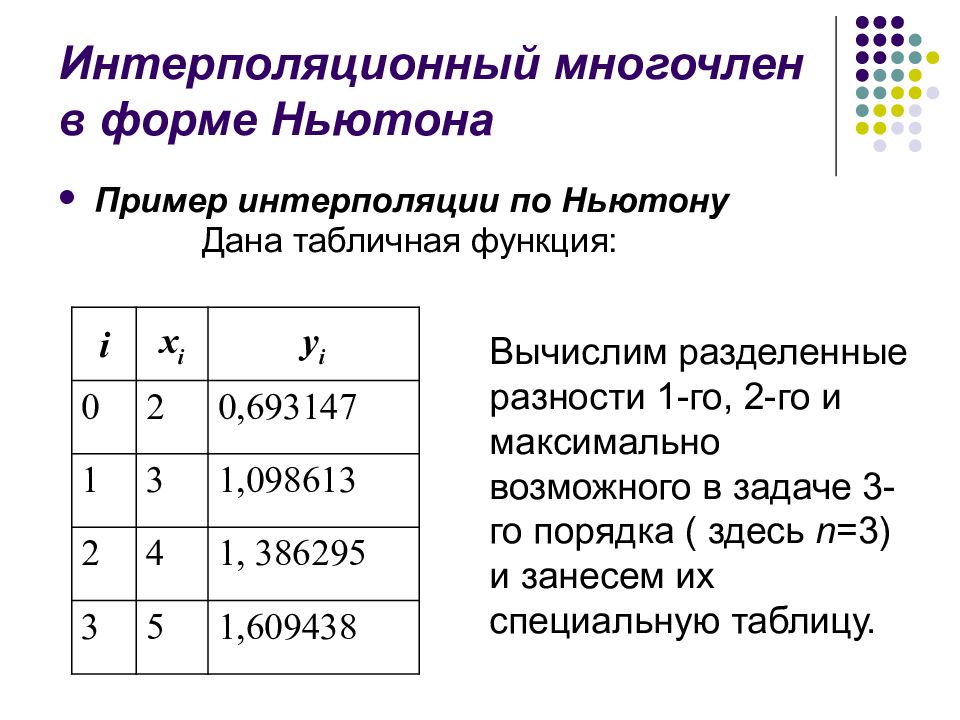
Пример интерполяции по Ньютону Дана табличная функция: i x i y i 0 2 0,693147 1 3 1,098613 2 4 1, 386295 3 5 1,609438 Вычислим разделенные разности 1-го, 2-го и максимально возможного в задаче 3-го порядка ( здесь n =3) и занесем их специальную таблицу.
Слайд 52: Интерполяционный многочлен в форме Ньютона
Три разделенные разности первого порядка:
Слайд 53: Интерполяционный многочлен в форме Ньютона
Две разделенные разности второго порядка:
Слайд 54: Интерполяционный многочлен в форме Ньютона
Одна разделенная разность третьего порядка:
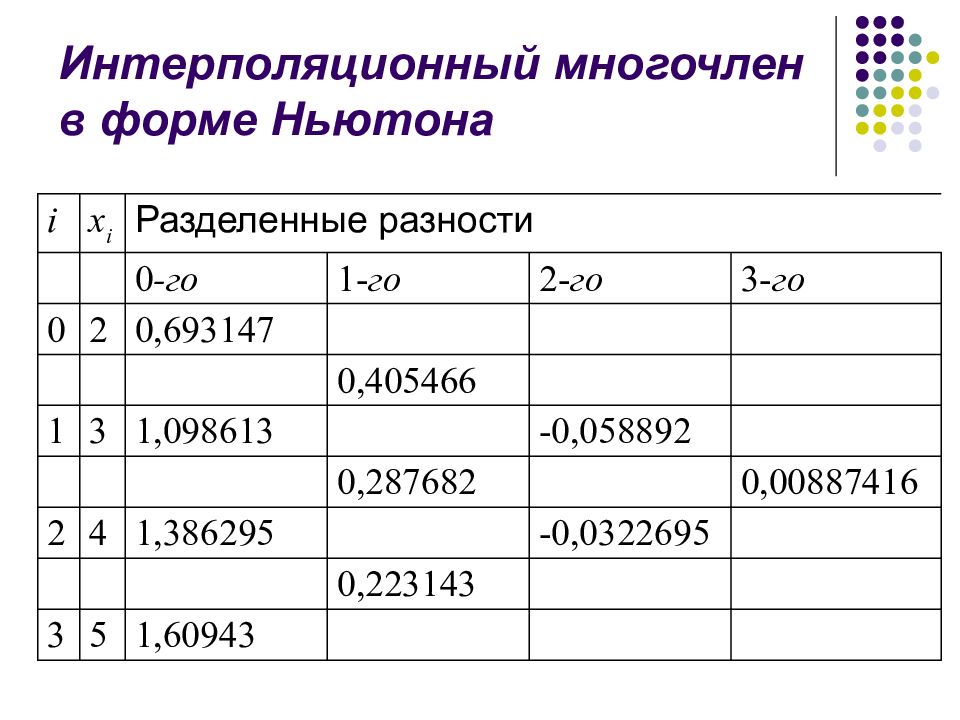
Слайд 55: Интерполяционный многочлен в форме Ньютона
i x i Разделенные разности 0 -го 1- го 2- го 3- го 0 2 0,693147 0,405466 1 3 1,098613 -0,058892 0,287682 0,00887416 2 4 1,386295 -0,0322695 0,223143 3 5 1,60943
Слайд 56: Интерполяционный многочлен в форме Ньютона
Интерполяционный многочлен Ньютона для заданной табличной функции имеет вид: