Числовым рядом называется сумма вида: где числа u 1, u 2, u 3,…,u n,... – члены ряда (бесконечная последовательность), u n – общий член ряда. Частичные суммы ряда : S 1 =u 1, S 2 =u 1 +u 2, S 3 =u 1 +u 2 +u 3, ………………….. S n =u 1 +u 2 +u 3 +…+u n
Если или, то ряд называется сходящимся, а число S – суммой сходящегося ряда. Если частичная сумма S n ряда при неограниченном возрастании n не имеет конечного предела (в частности, стремится к +∞ или к -∞), то такой ряд называется расходящимся.
Пример. Найти сумму членов ряда: Находим частичные суммы членов ряда:
Запишем последовательность частичных сумм: … Общий член этой последовательности есть: n/(2n+1) Последовательность частичных сумм имеет предел, равный 1/2. Итак, ряд сходится и его сумма равна 1/2.
Необходимый признак сходимости ряда Ряд может сходиться только при условии, что его общий член u n при неограниченном увеличении номера n стремится к нулю: Если, то ряд расходится – это достаточный признак расходимости ряда.
Достаточные признаки сходимости ряда с положительными членами а) Признак сравнения рядов с положительными членами. Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда: исследуемый ряд расходится, если его члены превосходят соответствующие члены другого заведомо расходящегося ряда. б) Признак Даламбера. Если для ряда с положительными членами выполняется условие, то ряд сходится при l< 1 и расходится при l> 1. Признак Даламбера не дает ответа, если l=1. В этом случае для исследования ряда применяют другие приемы.
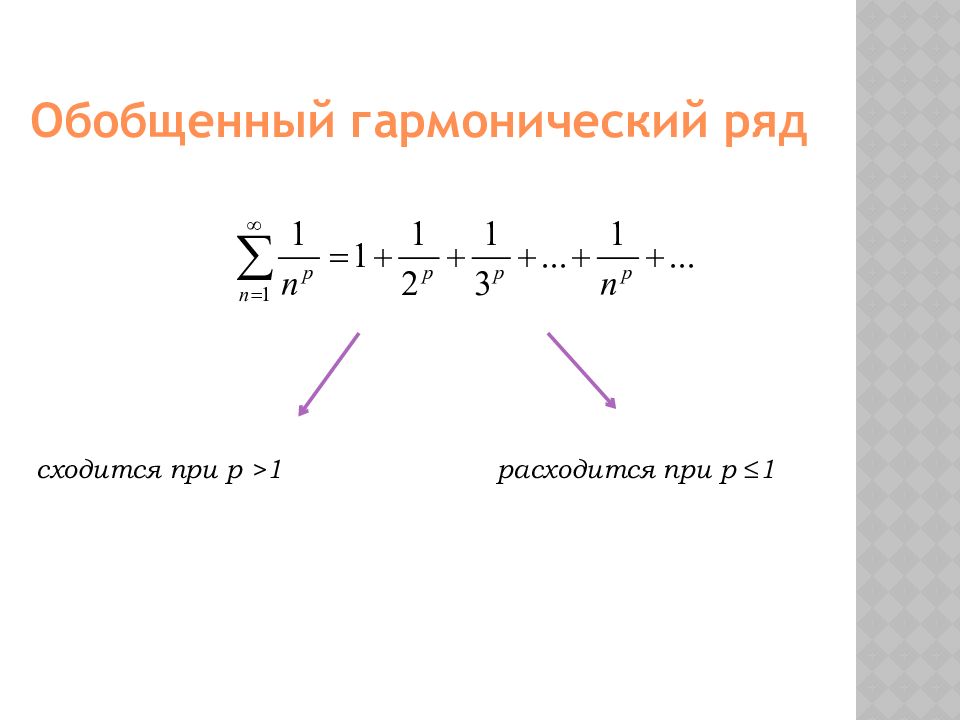
образован из членов геометрической прогрессии: Геометрический ряд сходится при | q | < 1 расходится при | q | ≥ 1
Обобщенный гармонический ряд сходится при p > 1 расходится при p ≤ 1
Пример. Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения: Необходимый признак сходимости ряда выполняется. Для признака сравнения сравним данный ряд с геометрическим: который сходится, так как q =1 / 2 < 1.
Сравнивая члены нашего ряда с соответствующими членами геометрического ряда, получим неравенства: Т.е. члены данного ряда соответственно меньше членов геометрического ряда. Следовательно, данный ряд сходится.
Пример. Исследовать сходимость ряда, используя признак Даламбера: Следовательно, данный ряд сходится.
Определение 1: Функциональным называется ряд, члены которого есть непрерывные функции от аргумента x : При x=n функциональный ряд становится числовым, который либо сходится, либо расходится.
Рассмотрим геометрическую прогрессию со знаменателем х : . Геометрическая прогрессия сходится, если ее знаменатель. Тогда она имеет сумму, которая очевидно является функцией от х.
Определение 2: Совокупность значений x, при которых ФР сходится, называется областью сходимости ряда. Сумма ФР может быть представлена:
Определение 3: ФР называется равномерно сходящимся в некоторой области X, если для каждого сколь угодно малого ε >0 найдется такое N( ε )>0, что при n>N выполняется неравенство: S(x) – непрерывная функция
Определение 4: Пусть даны: причем в некоторой области выполняется условие: Тогда
Если мажоранта функционального ряда сходится, то сходится и функциональный ряд абсолютно и равномерно.
Пусть даны функциональные ряды:
Определение 5: Функциональный ряд вида: называется степенным рядом.
Если степенной ряд сходится при x = x1, то он сходится для всех |x| < |x1|. Если степенной ряд расходится при x = x2, то он расходится для всех |x |> |x2|. Из теоремы следует, что существует такое положительное значение x = R, что при |x| < R степенной ряд сходится, а при |x| > R расходится, R - радиус сходимости. x0 x0 + R x0 - R Ряд сходится
По признаку Даламбера:
По радикальному признаку Коши:
Определение 6: Рядом Тейлора функции f(x) называется степенной ряд вида: это есть разложение функции в окрестности точки x 0. Коэффициентами являются производные высших порядков в точке x 0, т.е. Для разложения в ряд Тейлора необходимо, чтобы f(x) существовала в x 0 вместе со своими производными.
Определение 6: Всякая функция f(x) бесконечно дифференцируемая в интервале |x-x 0 |<r может быть разложена в степенной ряд Тейлора, если в этом интервале остаток ряда стремится к нулю:
Определение 7: Рядом Маклорена функции f(x) называется степенной ряд вида: это есть разложение функции в окрестности точки x =0. Коэффициентами являются производные высших порядков в точке x =0, т.е. Для разложения в ряд Маклорена необходимо, чтобы f(x) существовала в x =0 вместе со своими производными.
Определение. Ряд называется степенным по степеням х. Ряд является степенным по степеням.
Для любого степенного ряда существует конечное неотрицательное число R - радиус сходимости - такое, что если, то при ряд сходится, а при расходится. Интервал называется интервалом сходимости степенного ряда. Если, то интервал сходимости представляет собой всю числовую прямую. Если же, то степенной ряд сходится лишь в точке х =0.
Составим ряд из абсолютных величин членов степенного ряда и найдем интервал, в котором он будет сходиться, Тогда в этом интервале данный степенной ряд будет сходиться абсолютно. Согласно признаку Даламбера, если ,то степенной ряд абсолютно сходится для всех х, удовлетворяющих этому условию.
В этом случае ряд будет сходиться внутри интервала (- R,R ),где R -это радиус сходимости ряда: . За пределами этого интервала ряд будет расходиться, а на концах интервала, где , требуется дополнительное исследование.
Найти интервал сходимости ряда . Следовательно, ряд сходится абсолютно в интервале (-1,1).
Положим. Тогда получим числовой ряд. Этот ряд расходится (сравните его с гармоническим рядом). Полагая x = -1, имеем знакочередующийся ряд, который сходится условно в силу теоремы Лейбница. Итак, степенной ряд сходится в промежутке [-1,1).
Найти интервал сходимости степенного ряда. Здесь, =.Тогда = = =
=. Но 0<1 всегда, т.е. независимо от x. Это означает, что степенной ряд сходится независимо от x, т.е. на всей числовой прямой. Итак, интервал сходимости ряда - это промежуток.
Найти интервал сходимости ряда. = = = =. Этот предел может быть меньше единицы, если только x =0 (иначе он будет равен бесконечности). Это означает, что степенной ряд сходится лишь в точке x =0.
1. Сумма степенного ряда является непрерывной функцией в каждой точке интервала сходимости этого ряда. Например, непрерывна, если.
2. Ряд, полученный почленным дифференцированием степенного ряда, является степенным рядом с тем же интервалом сходимости, что и данный ряд, причем :если , то
3. Степенной ряд можно почленно интегрировать на любом промежутке, целиком входящем в интервал сходимости степенного ряда, при этом где.
Определение. Если бесконечно дифференцируемая функция является суммой степенного ряда, то говорят, что она разлагается в степенной ряд. Опр. Рядом Тейлора функции f ( x ) называется ряд, коэффициенты которого определяются по формулам, т.е. ряд или. Разложение функций в степенные ряды
Теорема. Если в некоторой окрестности точки , то ряд справа есть ее ряд Тейлора. Короче: если функция представлена в виде степенного ряда, то этот ряд является ее рядом Тейлора. Представление функции ее рядом Тейлора единственно.
Рассмотрим n - ю частичную сумму ряда Тейлора: Этот многочлен называется многочленом Тейлора функции. Разность называется остаточным членом ряда Тейлора.
Остаточный член в форме Лагранжа имеет вид: Тогда называется формулой Тейлора с остаточным членом в форме Лагранжа.
Для того чтобы функцию можно было разложить в ряд Тейлора на интервале (-R,R), необходимо и достаточно, чтобы функция на этом интервале имела производные всех порядков и чтобы остаточный член формулы Тейлора стремился к нулю при всех
Если функция f(x) на интервале (-R,R) бесконечно дифференцируема и ее производные равномерно ограничены в совокупности, т. е. существует такая константа М, что для всех выполняется условие при п=0,1,2,…, то функцию можно разложить в ряд Тейлора на этом интервале.
Все производные этой функции совпадают с самой функцией, а в точке х=0 они равны 1. Составим для функции формально ряд Маклорена: Этот ряд, очевидно, сходится на всей числовой оси. Но все производные функции равномерно ограничены, т. к., где R -любое число из интервала сходимости. Поэтому этот ряд сходится именно к функции
Вычислим производные синуса:
Ясно, что все производные синуса не превосходят по модулю единицу. Так что запишем ряд, который будет разложением синуса: при этом видно, что этот ряд сходится на всей числовой оси.
Разложения 1–7 позволяют, используя соответствующее разложение, вычислять приближенно значения функций, интегралы, приближенно интегрировать дифференциальные уравнения. Пример. С помощью степенного ряда вычислить с точностью до 0,0001 Применение степенных рядов
Разложим подынтегральную функцию в степенной ряд:
Так как получившийся ряд является знакочередующимся, то сумма знакочередующегося ряда не превосходит первого члена такого ряда. Ясно, что часть ряда, которую в задаче следует отбросить, также является знакочередующимся рядом и его сумма не превзойдет модуля первого отброшенного члена ряда. Таким образом, первый отброшенный член ряда должен быть меньше заданной погрешности, т.е. 0,0001.
Вычислив еще несколько членов ряда видим, что Отбросив этот и следующие за ним члены ряда, получим:
Вычислить с точностью до 0,001.Преобразуем Воспользуемся биномиальным рядом при х=0,25 и Получим
