Лектор Пахомова Е.Г. 20 1 0 г. Математический анализ Тема: Функция нескольких переменных
§1 1. Определение функции нескольких переменных. Предел и непрерывность ФНП 1. Определение функции нескольких переменных ОПРЕДЕЛЕНИЕ. Пусть X = {( x 1, x 2 , …, x n ) | x i X i ℝ } , U ℝ . Функция f : X U называется функцией n переменных. Записывают: u = f ( x 1, x 2 , …, x n ) , где f – закон, задающий соответствие между x 1, x 2 , …, x n и u . Значение u = f ( x 1, x 2 , …, x n ) при x 1 = x 0 1, x 2 = x 0 2, …, x n = x 0 n записывают в виде u = f ( x 0 1, x 0 2 , …, x 0 n ) или
Называют: X – область определения функции (Обозначают: D ( u ) ), x 1, x 2, …, x n – аргументы ( независимые переменные ), U – область значений (Обозначают: E ( u ) ), u ( u U ) – зависимая переменная ( функция ). СПОСОБЫ ЗАДАНИЯ ФНП 1) словесный; 2) табличный; 3) аналитический: а) явное задание (т.е. формулой u = f ( x 1, x 2 , …, x n ) ) б) неявное задание (т.е. уравнением F ( x 1, x 2 , …, x n, u ) = 0 ). 4) Функцию z = f ( x, y ) можно задать графически. ОПРЕДЕЛЕНИЕ. График о м функции z = f ( x, y ) называется геометрическое место точек пространства с координатами ( x ; y ; f ( x, y )), ( x, y ) D( z ). График функции z = f ( x, y ) будем также называть «поверх - ностью z = f ( x, y ) ».
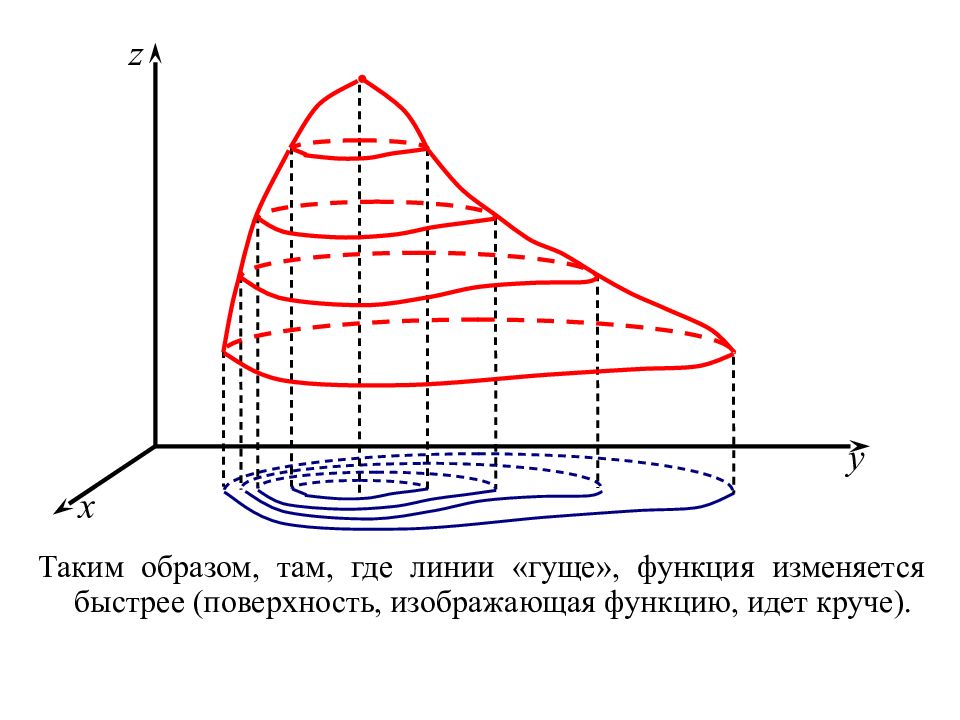
Линией уровня функции z = f ( x, y ) называют геометрическое место точек ( x, y ) плоскости, в которых функция принимает одно и то же значение C. 1) Линия уровня – линия в D ( z ), которая имеет уравнение f ( x, y ) = C . 2) Линия уровня – проекция на плоскость xOy линии пере - сечения графика функции z = f ( x, y ) и плоскости z = C. Полагаем C равными C 1, C 1 + h, C 1 + 2 h, …, C 1 + nh. Получим линии уровня, по расположению которых можно судить о графике функции и, следовательно, о характере изменения функции.
Таким образом, там, где линии «гуще», функция изменяется быстрее (поверхность, изображающая функцию, идет круче).
Поверхностью уровня функции u = f ( x, y, z ) называют геометри - ческое место точек пространства Oxyz, в которых функция принимает одно и то же значение C. Уравнение поверхности уровня: f ( x, y, z ) = C . 2. Предел функции нескольких переменных Напомним: Число A ℝ называется пределом функции f ( x ) при x стремящемся к x 0 (пределом функции f ( x ) в точке x 0 ), если >0 >0 такое, что если x U * ( x 0, ), то f ( x ) U ( A, ).
( x, y ) M xOy ; z = f ( x, y ) = f ( M ), где M D xOy . ( x, y, z ) M Oxyz u = f ( x, y, z ) = f ( M ), где M D Oxyz . По аналогии, последовательность ( x 1, x 2 , …, x n ) будем считать декартовыми координатами точки n -мерного пространства и рассматривать функцию n переменных как функцию точки этого пространства. Обозначают: ℝ n – n -мерное пространство, u = f ( M ) , где M ( x 1, x 2 , …, x n ) ℝ n – функции n переменных.
Если M 1 ( x 1 ), M 2 ( x 2 ) Ox , то расстояние между ними (обознач а- ют: | M 1 M 2 |) находится по формуле: Если M 1 ( x 1, y 1 ), M 2 ( x 2, y 2 ) xOy , то Если M 1 ( x 1, y 1, z 1 ), M 2 ( x 2, y 2, z 2 ) Oxyz , то Обобщая эти формулы, будем считать, что расстояние между точками n -мерного пространства M 1 ( x 1, x 2 , …, x n ), M 2 ( y 1, y 2 , …, y n ) ℝ n равно
Пусть M 0 ( x 01, x 02 , …, x 0 n ) ℝ n . Множество точек ℝ n , находя - щихся от M 0 на расстоянии меньшем , будем называть - окрестностью точки M 0 и обозначать U ( M 0, ). Иначе говоря, -окрестность M 0 ( x 01, x 02, …, x 0 n ) состоит из таких точек M ( x 1, x 2 , …, x n ), для которых имеет место неравенство П ри n = 1 U( M 0, ) = { M Ox | | M 0 M | = | x – x 0 | < } = ( x 0 – , x 0 + ) . П ри n = 2 т.е. U ( M 0, ) точки M 0 ( x 0, y 0 ) – круг с центром в точке M 0 ( x 0, y 0 ) и радиусом . П ри n = 3 т.е. U ( M 0, ) точки M 0 ( x 0, y 0, z 0 ) – шар с центром в точке M 0 ( x 0, y 0, z 0 ) и радиусом .
-окрестность точки M 0 ℝ n без самой точки M 0 будем называть проколотой и обозначать U *( M 0, ) Пусть функция n переменных u = f ( M ) определена в некоторой окрестности точки M 0 ℝ n, кроме, может быть, самой M 0. ОПРЕДЕЛЕНИЕ. Число A ℝ называется пределом функции f ( M ) при M стремящемся к M 0 (пределом функции f ( M ) в точке M 0 ), если >0 >0 такое, что если M U * ( M 0, ), то f ( M ) U ( A, ). Записывают в общем случае: Для функции z = f ( x, y ):
Замечания. 1) Условие M U * ( M 0, ) означает, что выполняется неравен- ство: 2) Условие f ( M ) U ( A, ) означает, что для f ( M ) выполняется неравенство | f ( M ) – A | < 3) Так как формально определение предела функции n пере- менных ничем не отличается от определения предела функции одной переменной, то все утверждения, которые были получены о пределах функции одной переменной и в которых не используется упорядоченность точек числовой прямой, остаются верными и для предела функции n переменных. 4) Определение бесконечно большой функции переносится на случай функции n переменных тоже дословно (сформулировать самостоятельно).
Пусть u = f ( M ) определена в некоторой окрестности M 0 ℝ n. ОПРЕДЕЛЕНИЕ 1. Функция f ( M ) называется непрерывной в точке M 0 если справедливо равенство или, иначе говоря, если >0 >0 такое, что если M U ( M 0, ) (т.е. | MM 0 | < ), то f ( M ) U ( f ( M 0 ), ) (т.е. | f ( M ) – f ( M 0 ) | < ). Справедливы утверждения: 1) арифметические операции над непрерывными в точке M 0 функциями приводят к непрерывным в этой точке функциям (при условии, что деление производится на функцию, не обращающуюся в ноль); 2) сложная функция, составленная из нескольких непрерывных функций, тоже будет непрерывной.
Если функция u = f ( M ) определена в некоторой окрестности точки M 0 (за исключением, может быть, самой M 0 ), но не является в этой точке непрерывной, то ее называют разрывной в точке M 0, а саму точку M 0 – точкой разрыва. Пусть G – некоторое множество точек в ℝ n и M 0 G . Точка M 0 называется внутренней точкой множества G, если U( M 0, ) G. Множество, каждая точка которого – внутренняя, называется открытым. Точка M 0 называется граничной точкой множества G, если в любой ее -окрестности есть как точки из G, так и точки, не принадлежащие G. Множество всех граничных точек множества G называется его границей. Множество, содержащее свою границу, называется замкнутым.
Множество G называется связным, если любые две его точки можно соединить непрерывной кривой, состоящей из точек этого множества. Замечание. Непрерывной кривой в n - мерном пространстве называется геометрическое место точек M ( x 1, x 2 , …, x n ), координаты которых удовлетворяют уравнениям x 1 = x 1 ( t ) , x 2 = x 2 ( t ) , …, x n = x n ( t ) , где x 1 = x 1 ( t ) , x 2 = x 2 ( t ) , …, x n = x n ( t ) – непрерывные функции параметра t ( ; ). Связное открытое множество называется областью. Связное замкнутое множество называется замкнутой областью. Область, целиком лежащая в некоторой -окрестности точки O (0,0,…,0), называется ограниченной.
ТЕОРЕМА (аналог теорем Вейерштрасса и Коши для ФНП). Если функция n переменных u = f ( M ) непрерывна в замкнутой и ограниченной области D, то она 1) ограничена ; 2) достигает в D своего наибольшего и наименьшего зна - чения ; 3) принима е т все промежуточные значения между любыми двумя своими значениями.
Для наглядности, здесь и далее все определения и утверждения будем формулировать для функции 2-х (или 3-х) переменных. На случай большего числа неизвестных они обобщаются естественным образом. Пусть z = f ( x, y ) , D ( z ) = D xOy , D – открытая область. Пусть M 0 ( x 0, y 0 ) D . Придадим x 0 приращение x, оставляя значение y 0 неиз - мененным (так, чтобы точка M ( x 0 + x, y 0 ) D ). При этом z = f ( x, y ) получит приращение x z ( M 0 ) = f ( M ) – f ( M 0 ) = f ( x 0 + x, y 0 ) – f ( x 0, y 0 ). x z ( M 0 ) называется частным приращением функции z = f ( x, y ) по x в точке M 0 ( x 0, y 0 ).
ОПРЕДЕЛЕНИЕ. Предел при x 0 отношения (если он существует и конечен) называется частной производной функции z = f ( x, y ) по переменной x в точке M 0 ( x 0, y 0 ). Обозначают: или
Замечани я. 1) Обозначения и надо понимать как целые символы, а не как частное двух величин. Отдельно взятые выражения z ( x 0, y 0 ) и x смысла не имеют. 2) характеризует скорость изменения функции z = f ( x, y ) по x в точке M 0 ( x 0, y 0 ) (физический смысл частной производной по x ). Аналогично определяется частная производная функции z = f ( x, y ) по переменной y в точке M 0 ( x 0, y 0 ): Обозначают:
Соответствие (и ) является функцией, определенной на D 1 ( D 2 ) D ( f ). Ее называют частной производной функции z = f ( x, y ) по переменной x ( y ) и обозначают Операция нахождения для функции z = f ( x, y ) ее частных производных называется дифференцированием функции z = f ( x, y ) по переменной x и y соответственно.
Фактически, – это обыкновенная про - изводная функции z = f ( x, y ), рассматриваемой как функция одной переменной x (соответственно y ) при постоянном значении другой переменной. Поэтому, вычисление частных производных производится по тем же самым правилам, что и для функции одной переменой. При этом, одна из переменных считается константой. ПРИМЕР. Найти частные производные по x и по y функции f ( x, y ) = x 2 + xy 2 + y 3
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ частных производных функции ДВУХ ПЕРЕМЕННЫХ. Пусть функция z = f ( x, y ) имеет в M 0 ( x 0, y 0 ) частную произ - водную по x ( y ). Пусть поверхность S – график функции z = f ( x, y ). Тогда где ( ) – угол наклона к оси Ox ( Oy ) касательной, проведен - ной в точке P 0 ( x 0, y 0, f ( x 0, y 0 ) ) к линии пересечения поверхнос - ти S и плоскости y = y 0 ( x = x 0 ).
Пусть z = f ( x, y ) имеет и, определенные на D xOy . Функции и называют также частными производными первого порядка функции f ( x, y ) (или первыми частными производными функции f ( x, y ) ). и в общем случае функции переменных x и y . Частные производные по x и по y от и, если они существуют, называются частными производ - ными второго порядка (или вторыми частными производ - ными ) функции f ( x, y ).
Обозначения.
Частные производные второго порядка в общем случае являют - ся функциями двух переменных. Их частные производные (если они существуют) называют частными производными третьего порядка (или третьими частными производными ) функции z = f ( x, y ). Продолжая этот процесс, назовем частными производными порядка n функции z = f ( x, y ) частные производные от ее частных производных ( n – 1)-го порядка. Обозначения аналогичны обозначениям для частных производ - ных 2-го порядка. Например: Частные производные порядка n > 1 называют частными производными высших порядков.
Частные производные высших порядков, взятые по разным аргументам, называются смешанными. Частные производные высших порядков, взятые по одному аргументу, называют иногда несмешанными. ПРИМЕР. Найти частные производные 2-го порядка от функции z = x 4 + 3 x 2 y 5 . ТЕОРЕМА 1 (условие независимости смешанной производной от последовательности дифференцирований). Пусть z = f ( x, y ) в некоторой области D xOy имеет все частные производные до n -го порядка включительно и эти производные непрерывны. Тогда смешанные производные порядка m ( m n ), отлича - ющиеся лишь последовательностью дифференцирований, совпадают между собой.
1. Дифференцируемые функции нескольких переменных Пусть z = f ( x, y ) , D ( z ) = D xOy , D – область (т.е. открытое связное множество). Пусть M 0 ( x 0, y 0 ) D . Придадим x 0 и y 0 приращение x и y соответственно (так, чтобы точка M ( x 0 + x, y 0 + y ) D ). При этом z = f ( x, y ) получит приращение z ( M 0 ) = f ( M ) – f ( M 0 ) = f ( x 0 + x, y 0 + y ) – f ( x 0, y 0 ). z ( M 0 ) называется полным приращением функции z = f ( x, y ) в точке M 0 ( x 0, y 0 ), соответствующим x и y.
ОПРЕДЕЛЕНИЕ. Функция z = f ( x, y ) называется дифференци - руемой в точке M 0 ( x 0, y 0 ) если ее полное приращение в этой точке может быть записано в виде z ( M 0 ) = A x + B y + 1 x + 2 y , (1) где A, B – некоторые числа, 1, 2 – бесконечно малые при x 0, y 0 (или, что то же, при ). Замечание. Функции 1 и 2 зависят от x 0, y 0, x, y. Равенство (1) можно записать и в более сжатой форме: z ( M 0 ) = A x + B y + , ( 2 ) где – бесконечно малая при 0. Функция z = f ( x, y ), дифференцируемая в каждой точке некото - рой области D, называется дифференцируемой в D.
Напомним: для дифференцируемой функции y = f ( x ) справед- ливы утверждения: 1) y = f ( x ) дифференцируема в x 0 f ( x 0 ); 2) y = f ( x ) дифференцируема в x 0 y = f ( x ) непрерывна в x 0 . ТЕОРЕМА 1 (необходимые условия дифференцируемости ФНП) Пусть функция z = f ( x, y ) дифференцируема в точке M 0 ( x 0, y 0 ). Тогда она непрерывна в этой точке и имеет в ней частные производные по обеим независимым переменным. Причем ДОКАЗАТЕЛЬСТВО
Замечания. 1) С учетом теоремы 1 равенства (1) и (2) можно записать соответственно в виде: (3) (4) где 1, 2 – бесконечно малые при x 0, y 0, – бесконечно малая при 0. 2) Утверждение обратное теореме 1 неверно. Из непрерывности функции двух переменных в точке и существования в этой точке ее частных производных еще не следует дифферен - цируемость функции.
ПРИМЕР. Функция непрерывна в точке (0;0) и имеет в этой точке частные производные, но не явля - ется в этой точке дифференцируемой. ТЕОРЕМА 2 (достаточные условия дифференцируемости ФНП) Пусть функция z = f ( x, y ) имеет в некоторой окрестности точки M 0 ( x 0, y 0 ) частные производные и, причем в самой точке M 0 эти производные непрерывны. Тогда функция z = f ( x, y ) дифференцируема в этой точке.
Пусть функция z = f ( x, y ) дифференцируема в точке M 0 ( x 0, y 0 ). Тогда где 1, 2 – бесконечно малые при x 0, y 0. ОПРЕДЕЛЕНИЕ. Если z = f ( x, y ) дифференцируема в точке M 0 ( x 0, y 0 ), то линейная относительно x и y часть ее пол - ного приращения в этой точке, т.е. называется полным дифференциалом функции z = f ( x, y ) в точке M 0 ( x 0, y 0 ) и обозначается dz ( M 0 ) или df ( x 0, y 0 ).
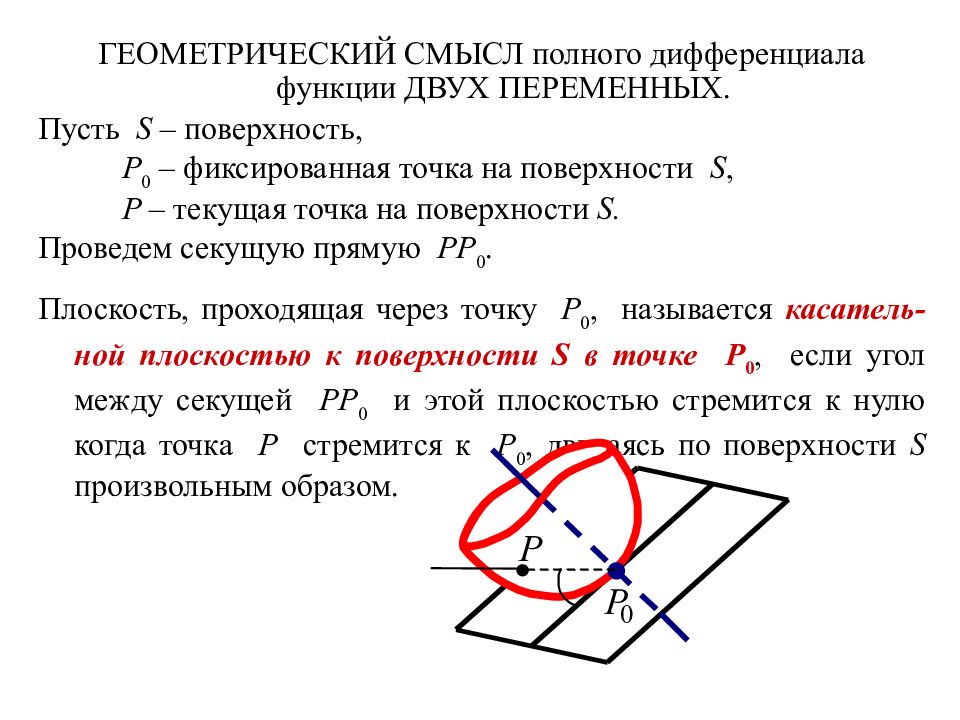
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ полного дифференциала функции ДВУХ ПЕРЕМЕННЫХ. Пусть S – поверхность, P 0 – фиксированная точка на поверхности S, P – текущая точка на поверхности S. Проведем секущую прямую PP 0. Плоскость, проходящая через точку P 0, называется касатель - ной плоскостью к поверхности S в точке P 0, если угол между секущей PP 0 и этой плоскостью стремится к нулю когда точка P стремится к P 0, двигаясь по поверхности S произвольным образом.
Прямая, проходящая через точку P 0 перпендикулярно касатель - ной плоскости к поверхности в этой точке, называется нормалью к поверхности в точке P 0. ДОКАЗАНО, что 1) если функция z = f ( x, y ) дифференцируема в точке M 0 ( x 0, y 0 ), то поверхность z = f ( x, y ) имеет в точке P 0 ( x 0, y 0, f ( x 0, y 0 )) касательную плоскость. Ее уравнение: уравнение нормали к поверхности z = f ( x, y ) в P 0 ( x 0, y 0, f ( x 0, y 0 )):
2) если поверхность задана уравнением F ( x, y, z ) = 0, F ( x, y, z ) – дифференцируема в P 0 ( x 0, y 0, z 0 ), причем хотя бы одна из ее частных производных не обращается в P 0 в ноль, то касательная плоскость к поверхности в точке P 0 ( x 0, y 0, z 0 ) существует и ее уравнение уравнения нормали к поверхности F ( x, y, z ) = 0 в P 0 ( x 0, y 0, z 0 ): Замечание. Точка P 0 ( x 0, y 0, z 0 ) поверхности F ( x, y, z ) = 0, в которой все частные производные функции F ( x, y, z ) обращаются в ноль, называется особой точкой поверхности.
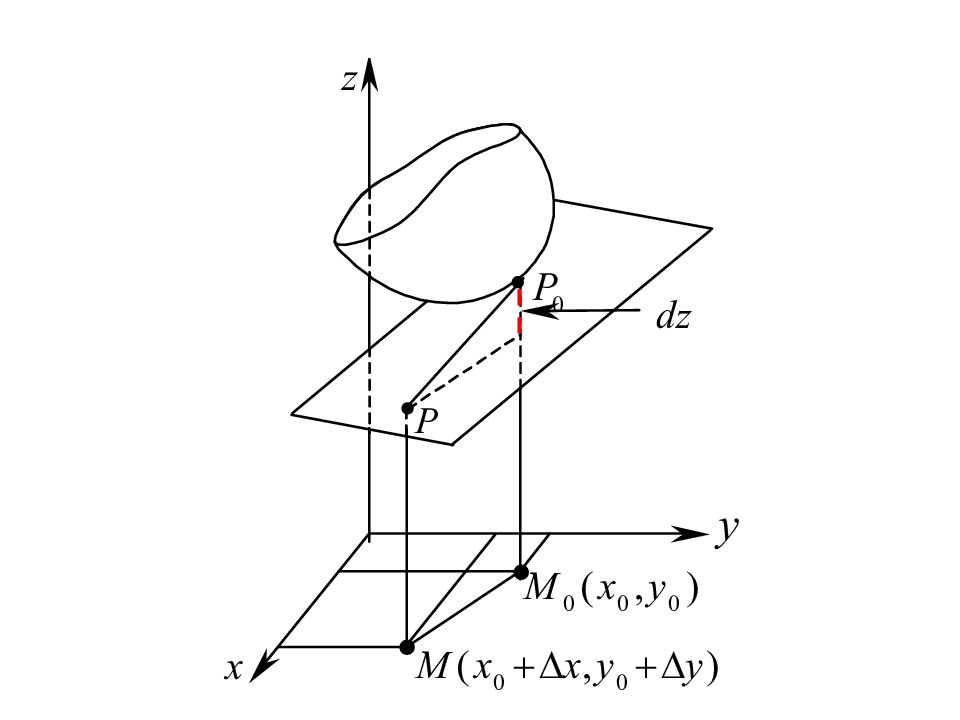
Пусть функция z = f ( x, y ) дифференцируема в точке M 0 ( x 0, y 0 ). поверхность z = f ( x, y ) имеет в точке P 0 ( x 0, y 0, f ( x 0, y 0 )) касательную плоскость. Ее уравнение: Обозначим x – x 0 = x, y – y 0 = y. Тогда уравнение касательной плоскости примет вид: ТАКИМ ОБРАЗОМ, полный дифференциал функции z = f ( x, y ) в точке M 0 ( x 0, y 0 ) равен приращению, которое получает аппликата точки P 0 ( x 0, y 0, f ( x 0, y 0 )) касательной плоскости к поверхности z = f ( x, y ), когда ее координаты x 0 и y 0 получают приращения x и y соответственно.
Очевидно, что соответствие ( x 0, y 0, x, y ) df ( x 0, y 0 ) является функцией (четырех переменных). Ее называют полным дифференциалом функции z = f ( x, y ) и обозначают dz или df ( x, y ). Легко доказать, что полный дифференциал функции n пере - менных обладает теми же свойствами, что и дифференциал функции одной переменной. В частности, для df ( x, y ) существует вторая, инвариантная форма записи :
Пусть z = f ( x, y ) дифференцируема в области D 1 D ( f ) . Ее д ифференциал dz ( M ) – функци я переменных x, y, d x, d y. Далее будем dz ( M ) называть дифференциалом 1- го порядка. Зафиксируем значение dx и d y. Тогда dz ( M ) станет функцией двух переменных x и y. Дифференциал функции dz ( M ) (если он существует) называется дифференциалом 2- го порядка функции z = f ( x, y ) (или вто - рым дифференциалом функции z = f ( x, y ) ) и обозначается d 2 z, d 2 f ( x, y ). d 2 z ( M ) – функция переменной x и y. Д ифференциал функции d 2 z ( M ) (если он существует) называют дифференциалом третьего порядка функции z = f ( x, y ) (или третьим дифференциалом функции z = f ( x, y ) ) и обозна - чается d 3 z, d 3 f ( x, y ).
Продолжая далее этот процесс, определим дифференциал n -го порядка функции z = f ( x, y ) как дифференциал от ее диффе - ренциала порядка n – 1. Обозначают: d n z, d n f ( x, y ). Замечание. Значение дифференциала n -го порядка функции f ( x, y ) в точке ( x 0, y 0 ) обозначают d n z ( M 0 ), d n f ( x 0, y 0 ) . Дифференциалы порядка n > 1 называют дифференциалами высших порядков. Если функция z = f ( x, y ) имеет дифференциал порядка n, то ее называют n раз дифференцируемой. ТЕОРЕМА 3 (о связи дифференциала n -го порядка и n -х частных производных). Если все производные k -го порядка функции z = f ( x, y ) в области D непрерывны, то она k раз дифференцируема. При этом имеет место символическая формула
Замечание. 1) Чтобы записать дифференциал по формуле (6) необходимо: а) формально раскрыть скобку по биномиальному закону, б) умножить получившееся выражение на f ( x, y ), в) замени ть каждое произведение частной производной Например, для n = 2 получим: Для n = 3 получим:
2) Символическая формула для нахождения дифференциала d k u функции u = f ( x 1, x 2,… x n ) будет иметь вид при условии, что x 1, x 2,… x n – независимые аргументы.
1. Частные производные сложной функции Пусть z = f ( x, y ), где x = 1 ( u, v ), y = 2 ( u, v ). Тогда z – сложная функция независимых переменных u и v. Переменные x и y называются для z промежуточными переменными. ЗАДАЧА: найти частные производные функции z по u и v. ТЕОРЕМА 1 ( о производной сложной функции). Пусть z = f ( x, y ), где x = 1 ( u, v ), y = 2 ( u, v ). Если f ( x, y ), 1 ( u, v ), 2 ( u, v ) дифференцируемы, то справедливы формулы ( 1 )
Теорема 1 естественным образом обобщается на случай функции большего числа независимых и промежуточных аргументов. А именно, если u = f ( x 1, x 2 , …, x n ), где x i = i ( t 1, t 2 , …, t m ) (i = 1,2, …, n ), то
ЧАСТНЫЕ СЛУЧАИ сложной ФНП 1) Пусть z = f ( x, y ), где x = 1 ( t ), y = 2 ( t ). Тогда z – сложная функцией одной переменной t. Если f ( x, y ), 1 ( t ), 2 ( t ) дифференцируемы, то справедлива формула ( 2 ) 2) Пусть z = f ( x, y ), где y = ( x ) Тогда z – сложная функцией одной переменной x. Если f ( x, y ), ( x ) дифференцируемы, то справедлива формула ( 3 ) Производная в левой части формулы ( 3 ) называется полной производной функции z.
Пусть z = f ( x, y ) – дифференцируемая функция 2- х независимых переменных. Тогда, по определению ( 4 ) или, в другом виде, ( 5 ) Формула ( 5 ) остается верна и в том случае, если z = f ( x, y ) – слож - ная функция. Формула ( 5 ) записи полного дифференциала называется инвариантной. УПРАЖНЕНИЕ 1. Показать, что формула ( 4 ) неверна, если x и y – функции.
Пусть z = f ( x, y ) – n раз дифференцируемая функция 2- х незави - симых переменных. Тогда k n ( 6 ) Формула ( 6 ) тоже не является инвариантной. УПРАЖНЕНИЕ 2. Найти дифференциал 2-го порядка если z = f ( x, y ), где x = 1 ( u, v ), y = 2 ( u, v ).
ТЕОРЕМА 1 (существования неявной функции). Пусть функция F ( x 1, x 2 , …, x n , u ) и все ее частные произ - водные 1- го порядка определены и непрерывны в некоторой окрестности точки P 0 ( x 01 , x 02 , …, x 0 n , u 0 ). Если F ( P 0 ) = 0 и, то такая окрестность U точки M 0 ( x 01 , x 02 , …, x 0 n ), в которой уравнение F ( x 1, x 2 , …, x n , u ) = 0 определяет непрерывную функцию u = f ( x 1, x 2 , …, x n ), причем 1) f ( M 0 ) = u 0 ; 2) для любой точки M ( x 1, x 2 , …, x n ) U 3) функция u = f ( x 1, x 2 , …, x n ) имеет в окрестности U непрерывные частные производные по всем аргументам.
ЗАДАЧА. Найти частные производные неявно заданной функции. 1) Пусть F ( x, y ) удовлетворяет условиям теоремы 1 в некоторой окрестности P 0 ( x 0, y 0 ) Тогда уравнение F ( x, y ) = 0 определяет в некоторой окрестности U точки x 0, непрерывную функцию y = f ( x ). ( 1 ) 2) Пусть F ( x, y, z ) удовлетворяет условиям теоремы 1 в окрестности P 0 ( x 0, y 0, z 0 ). Тогда уравнение F ( x, y, z ) = 0 определяет в некоторой окрест - ности U точки M 0 ( x 0, y 0 ) непрерывную функцию z = f ( x, y ). Так как фактически это обыкновенная производная функ- ции z = f ( x, y ), рассматриваемой как функция одной пере- менной при постоянном значении другой, то по формуле ( 1 ) получаем
Пусть z = f ( x, y ) определена в некоторой области D xOy , M 0 ( x 0, y 0 ) D. ОПРЕДЕЛЕНИЕ 1. Точка M 0 ( x 0, y 0 ) называется точкой максимума функции f ( x, y ), если M ( x, y ) U ( M 0, ) выполняется неравенство f ( x, y ) f ( x 0, y 0 ) . Точка M 0 ( x 0, y 0 ) называется точкой минимума функции f ( x, y ), если M ( x, y ) U ( M 0, ) выполняется неравенство f ( x, y ) f ( x 0, y 0 ) . Точки максимума и минимума функции называются ее точками экстремума. Значения функции в точках максимума и минимума называются соответственно максимумами и минимумами ( экстремумами ) этой функции.
Замечания. 1) По смыслу точкой максимума (минимума) функции f ( x, y ) могут быть только внутренние точки области D. 2) Если M ( x, y ) U *( M 0, ) выполняется неравенство f ( x, y ) < f ( x 0, y 0 ) [ f ( x, y ) > f ( x 0, y 0 ) ], то точку M 0 называют точкой строгого максимума (соответственно точкой строгого минимума ) функции f ( x, y ). Определенные в 1 точки максимума и минимума называют иногда точками нестрогого максимума и минимума. 3) Понятия экстремумов носят локальный характер. В рассматриваемой области функция может совсем не иметь экстремумов, может иметь несколько (в том числе бесчисленно много) минимумов и максимумов. При этом некоторые минимумы могут оказаться больше некоторых ее максимумов.
ТЕОРЕМА 2 (необходимые условия экстремума). Если функция z = f ( x, y ) в точке M 0 ( x 0, y 0 ) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю, либо хотя бы одна из них не существует. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ теоремы 2. Если M 0 ( x 0, y 0 ) – точка экстремума функции z = f ( x, y ), то касательная плоскость к графику этой функции в точке P 0 ( x 0, y 0, f ( x 0, y 0 )) либо параллельна плоскости xOy, либо вообще не существует. ДОКАЗАТЕЛЬСТВО Точки, удовлетворяющие условиям теоремы 2, называются критическими точками функции z = f ( x, y ).
ТЕОРЕМА 3 (достаточные условия экстремума функции ДВУХ переменных). Пусть M 0 ( x 0, y 0 ) – критическая точка функции z = f ( x, y ) и в некоторой окрестности точки M 0 функция имеет непрерыв - ные частные производные до 2 - го порядка включительно. Обозначим Тогда 1) если A C – B 2 < 0 , то точка M 0 ( x 0, y 0 ) не является точкой экстремума; 2) если A C – B 2 > 0 и A > 0 , то в точке M 0 ( x 0, y 0 ) функция имеет минимум; 3) если A C – B 2 > 0 и A < 0 , то в точке M 0 ( x 0, y 0 ) функция имеет максимум; 4) если A C – B 2 = 0 , то никакого заключения о крити - ческой точке M 0 ( x 0, y 0 ) сделать нельзя и требуются дополнительные исследования.
Замечание. 1) Если с помощью теоремы 3 исследовать критическую точку M 0 ( x 0, y 0 ) не удалось, то ответ на вопрос о наличии в M 0 экстремума даст знак f ( x 0, y 0 ) : а) если при всех достаточно малых x и y имеем f ( x 0, y 0 ) < 0, то M 0 ( x 0, y 0 ) – точка строгого максимума; б) если при всех достаточно малых x и y имеем f ( x 0, y 0 ) > 0, то M 0 ( x 0, y 0 ) – точка строгого минимума. В случае нестрогих экстремумов при некоторых значениях x и y приращение функции будет нулевым 2) Определения максимума и минимума и необходимые условия экстремума легко переносятся на функции трех и более числа переменных. Достаточные условия экстремума для функции n ( n > 2) переменных ввиду их сложности в данном курсе не рассматриваются. Определять характер критических точек для них мы будем по знаку приращения функции.
ОПРЕДЕЛЕНИЕ. Условным экстремумом функции n переменных u = f ( x 1, x 2 , …, x n ) называется экстремум этой функции, найденный в предположении, что переменные x 1, x 2 , …, x n связаны m ( m < n ) условиями : 1 ( x 1, x 2 , …, x n ) = 0 , ……………………., (1) m ( x 1, x 2 , …, x n ) = 0 . Условия (1) называются уравнениями связи. Обычный экстремум при этом называют безусловным экстремумом.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ условного экстрему - ма функции ДВУХ переменных. Пусть поверхность S – график функции z = f ( x, y ); M 1 – точка безусловного экстремума ( сравниваем P 1 и точ - к и ее полной окрестности). Пусть ℓ xOy – кривая уравнения связи ( x, y ) = 0, L – образ ℓ на поверхности S. M 0 – точка условного экстремума (сравниваем положе- ние P 0 и точек кривой L ).
ЗАДАЧА. Найти экстремум функции z = f ( x, y ), при условии, что x и y связаны условием ( x, y ) = 0. I способ. Метод подстановки. И з уравнения ( x, y ) = 0 выразить y = ( x ) и подставить в z = f ( x, y ). Тогда условный экстремум – обычный экстремум функции одной переменной z = f ( x, ( x )). II способ. Метод Лагранжа. Пусть уравнение ( x, y ) = 0 определяет функцию y = y ( x ) в неявном виде, f ( x, y ) – дифференцируемая. Необходимые условия условного экстремума функции 2-х переменных:
Замечания. 1) Условия (5) – необходимые условия экстремума функции 3-х переменных F ( x, y, ) = f ( x, y ) + ( x, y ). F ( x, y, ) называют функцией Лагранжа, – множителем Лагранжа. 2) ГЕОМЕТРИЧЕСКИЙ СМЫСЛ метода Лагранжа. Рассмотрим линии уровня f ( x, y ) = C 1 , …, f ( x, y ) = C k функции z = f ( x, y ) и кривую ( x, y ) = 0 (кривую ℓ ). Точка Q не является точкой условного экстремума, т.к. в ее окрестности функция принимает значения как больше C i , так и меньше C i . Точка условного экстремума M 0 – точка в которой ℓ касается некоторой линии уровня f ( x, y ) = C m .
В точке условного экстремума касательная к линии уровня f ( x, y ) = C m и к ℓ – общая. Угловой коэффициент касательной к линии уровня f ( x, y ) = C m в точке M 0 : Угловой коэффициент касательной к линии ℓ в точке M 0 : Так как k 1 = k 2 , то
Полученные из системы (5) критические точки M i необходимо проверить на наличие условного экстремума (рассмот реть в них приращение f ( M i ) с учетом уравнения связи ( x, y ) = 0). Замечание. Пусть M 0 ( x 0, y 0 ) – критическая точка условного экстремума, M 0 ( x 0, y 0 ) 0 . Рассмотрим f ( M 0 ) = f ( M ) – f ( M 0 ) = f ( x 0 + x, y 0 + y ) – f ( x 0, y 0 ) , где ( x 0, y 0 ) = 0 и ( x 0 + x, y 0 + y ) = 0 : f ( M 0 )= f ( x 0 + x, y 0 + y ) – f ( x 0, y 0 ) + 0 [ ( x 0 + x, y 0 + y ) – ( x 0, y 0 )] = = [ f ( x 0 + x, y 0 + y ) + 0 ( x 0 + x, y 0 + y )] – [ f ( x 0, y 0 ) + 0 ( x 0, y 0 )]. f ( M 0 ) = x,y F ( x 0, y 0, 0 ) Таким образом, приращение функции f ( M 0 ) с учетом уравнения связи ( x, y ) = 0 совпадает с приращением функции 2-х переменных F ( x, y, 0 ) = f ( x, y ) + 0 ( x, y ).
Для функции 2-х переменных справедлива ТЕОРЕМА 1 (достаточное условие условного экстремума функции 2-х переменных). Пусть M 0 ( x 0, y 0 ) – критическая точка для условного экстремума функции z = f ( x, y ) и в некоторой окрестности точки M 0 ( x 0, y 0 ) функция имеет непрерывные частные производные до второго порядка включительно. Обозначим Тогда : 1) если > 0 , то в точке M 0 – условный минимум ; 2) если < 0 , то в точке M 0 – условный максимум ; 3) если = 0 , то никакого заключения о критической точке M 0 ( x 0, y 0 ) сделать нельзя и требуются дополнительные исследования.
Обобщая полученные результаты на функцию n переменных получим следующие результаты. ТЕОРЕМА 2 (необходимые условия условного экстремума функции n переменных). Если функция u = f ( x 1, x 2 , …, x n ) в точке M 0 ( x 01, x 02 , …, x 0 n ) имеет условный экстремум, то M 0 является стационарной точкой функции F ( x 1, x 2 , …, x n, 1, … m ) = f ( M ) + 1 1 ( M ) + … + m m ( M ), где 1 ( M ) = 0 , … m ( M ) = 0 – уравнения связи. Наличие в критической точке M 0 экстремума определяют по знаку приращения функции n переменных F ( M 0, 01, … 0 m ) где 01, …, 0 m – фиксированные значения множителей Ла - гранжа, соответствующие точке M 0.
ОПРЕДЕЛЕНИЕ. Пусть G – некоторая область в простран - стве Oxyz [ на плоскости xOy ]. Говорят, что на G задано скалярное поле, если в каждой точке M G определена функция 3 -х переменных u = f ( M ) [ функция 2 -х переменных z = f ( M )]. Поведение скалярного поля характеризуют 1) производная по направлению; 2) градиент.
Пусть z = f ( x, y ) определена в области D xOy , M 0 ( x 0, y 0 ) D, s ̄ – некоторый вектор. Пусть M ( x 0 + x, y 0 + y ) D , такая, что ⇈ s ̄ ̄. ОПРЕДЕЛЕНИЕ. Если существует и конечен то его называют производной функции z = f ( x, y ) в точке M 0 ( x 0, y 0 ) по направлению вектора s ̄. Обозначают:
ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ ПО НАПРАВЛЕНИЮ – средняя скорость изменения функции z = f ( x, y ) на отрезке M 0 M . – скорость изменения функции z = f ( x, y ) в точке M 0 ( x 0, y 0 ) в направлении вектора s ̄ . Так же как и для функции одной переменной доказывается, что 1) если, то функция в точке M 0 ( x 0, y 0 ) в направле - нии вектора s ̄ возрастает; 2) если, то функция в точке M 0 ( x 0, y 0 ) в направле - нии вектора s ̄ убывает; 3) если, то в направлении вектора s ̄ функция не изменяется. направление вектора s ̄ – направление линии уровня функ - ции, проходящей через точку M 0 (вектор s ̄ является касательным к линии уровня в точке M 0 ).
Замечание. Частные производные функции являются частным случаем производной по направлению. А именно: – производная функции по направлению век - тора i (направлению оси Ox ); – производная функции по направлению век - тора j (направлению оси Oy ).
Пусть z = f ( x, y ) дифференцируема в точке M 0 ( x 0, y 0 ). Тогда где – бесконечно малая при Обозначим | M 0 M | = . Тогда x = cos , y = cos где cos , cos – направляющие ко синусы вектора s ̄ . Следовательно, Разделив на | M 0 M | = и перейдя к пределу при 0, полу - чим
где cos , cos – направляющие косинусы вектора s ̄ . Замечание. Аналогично определяется и обозначается производ - ная по направлению для функции 3-х переменных u = f ( x, y, z ). Для нее получим где cos , cos , cos – направляющие косинусы вектора s ̄.
ОПРЕДЕЛЕНИЕ. Градиентом функции z = f ( x, y ) в точке M 0 ( x 0, y 0 ) называется вектор с координатами Обозначают: grad z ( M 0 ). СВОЙСТВА ГРАДИЕНТА 1) grad z ( M 0 ) определяет направление, в котором функция в точке M 0 возрастает с наибольшей скоростью. При этом | grad z ( M 0 ) | равен наибольшей скорости изменения функции в точке M 0. 2) grad z ( M 0 ) перпендикулярен к линии уровня функции z = f ( x, y ), проходящей через точку M 0. Замечание. Для функции 3-х переменных градиент определя - ется и обозначается аналогичным образом, и сохраняет все свои свойства.
1. Формула Тейлора для функции одной переменной Пусть y = f ( x ) дифференцируема в окрестности точки x 0. Тогда f ( x 0 ) = f ( x 0 ) x + 1 x , где 1 ( x 0, x ) – бесконечно малая при x 0. f ( x 0 + x ) = f ( x 0 ) + f ( x 0 ) x + 1 x . (1) Обозначим x 0 + x = x , x = x – x 0 и формула (1) примет вид: f ( x ) = f ( x 0 ) + f ( x 0 ) ( x – x 0 ) + 1 ( x – x 0 ) , (2) где 1 ( x 0, x ) – бесконечно малая при x x 0.
Если y = f ( x ) n раз дифференцируема в окрестности точки x 0 , то применим n раз формулу (2) к функции i и получим (3): где n ( x 0, x ) – бесконечно малая при x x 0. Формулу (3) называют формулой Тейлора разложения функ - ции f ( x ) по степеням ( x – x 0 ) ( в окрестности точки x 0 ). Слагаемое называют многочленом Тейлора функции f ( x ) по степеням ( x – x 0 ). Слагаемое R n = n ( x – x 0 ) n называют остаточным членом формулы Тейлора.
Остаточный член R n можно записать в нескольких формах: 1) R n = n ( x – x 0 ) n = o (( x – x 0 ) n ) – форма Пеано ; 2) если y = f ( x ) n + 1 раз дифференцируема в окрестности точки x 0 , то R n можно записать в форме Лагранжа : где c – точка между x 0 и x. Если в формуле Тейлора x 0 = 0 , то она примет вид ( 4 ): Формулу ( 4 ) называют формулой Маклорена. Применение формулы Маклорена (Тейлора): 1) в приближенных вычислениях (значений функций, опреде - ленных интегралов и т.п.); 2) при нахождении пределов.
Пусть y = f ( x ) n раз дифференцируема в окрестности точки x 0 . Тогда d n f ( x 0 ) = f ( n ) ( x 0 ) ( x ) n . Если c – точка между x 0 и x , то (0; 1) такое, что c = x 0 + x . Следовательно, формулу (3) можно записать в виде
Пусть z = f ( x, y ) n + 1 раз дифференцируема в некоторой окрестности U точки M 0 ( x 0, y 0 ). Тогда, как и в случае функции y = f ( x ) справедлива формула где M ( x 0 + x, y 0 + y ) U и R n = o ( n ) при Формулу (5) называют формулой Тейлора для функции z = f ( x, y ) в окрестности точки M 0 ( x 0, y 0 ) ( по степеням ( x – x 0 ), ( y – y 0 ) ).
Слагаемое называют многочленом Тейлора функции f ( x, y ) в окрест - ности точки M 0 ( x 0, y 0 ). Слагаемое R n называют остаточным членом формулы Тейлора функции f ( x, y ) в окрестности точки M 0 ( x 0, y 0 ). Аналогичный вид имеет формула Тейлора для функций большего числа переменных
ОПРЕДЕЛЕНИЕ. Многочлен n переменных x 1, x 2 , …, x n в котором все члены имеют одинаковую степень, называется однородным или формой. ПРИМЕРЫ. 1) f ( x 1, x 2 , x 3 ) = 2 x 1 + 4 x 2 – 5 x 3 – однородный 1-й степени (линейная форма) ; 2) f ( x 1, x 2 ) = 2 x 1 2 + x 1 x 2 + 3 x 2 2 – однородный 2-й степени ( квадратичная форма ) ; 3) f ( x 1, x 2 ) = x 1 3 – x 1 2 x 2 + x 1 x 2 2 – 4 x 2 3 – однородный 3-й степени.
Общий вид квадратичной формы: f ( x 1, x 2 , …, x n ) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 + + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + … +2 a 1n x 1 x n + + 2 a 23 x 2 x 3 + 2 a 24 x 2 x 4 + … +2 a 2n x 2 x n + + … + 2 a n–1,n x n–1 x n . Будем считать, что a ij = a ji . Тогда квадратичную форму можно записать в виде
ОПРЕДЕЛЕНИЕ. Квадратичная форма f ( x 1, x 2 , …, x n ) называ - ется положительно ( отрицательно ) определенной если f ( x 1, x 2 , …, x n ) > 0 [ f ( x 1, x 2 , …, x n ) < 0] для любых, не равных одновременно нулю, значений переменных x 1, x 2 , …, x n. Положительно и отрицательно определенные квадратичные формы называются знакоопределенными. Если квадратичная форма может принимать как положительные, так и отрицательные значения, то она называется неопределенной. Симметрическая матрица из коэффициентов квадратичной формы, т.е. матрица вида называется матрицей квадратичной формы.
Главными угловыми минорами квадратной матрицы C = ( c ij ) называются ее миноры вида ТЕОРЕМА 1 (критерий Сильвестра). 1) Квадратичная форма положительно определена все главные угловые миноры ее матрицы – положительные. 2) Квадратичная форма отрицательно определена знаки главных угловых миноров ее матрицы чередуются, начиная с минуса, т.е.
Пусть z = f ( x, y ) , D ( z ) = D xOy , M 0 ( x 0, y 0 ) D . Пусть z = f ( x, y ) трижды дифференцируема в окрестности U точки M 0 и M 0 – критическая точка для z = f ( x, y ). Тогда 1) M U где R 2 = o ( 2 ) при 2) df ( M 0 ) = 0 и
Так как d 2 f ( M 0 ) – квадратичная форма с матрицей получаем следующие достаточные условия экстремума функции 2-х переменных: 1) функция z = f ( x, y ) имеет в точке M 0 ( x 0, y 0 ) максимум, если квадратичная форма d 2 f ( M 0 ) отрицательно определена, т.е. 2) функция z = f ( x, y ) имеет в точке M 0 ( x 0, y 0 ) минимум, если квадратичная форма d 2 f ( M 0 ) положительно определена, т.е.
