1
Слайд 2
Элементы аналитической геометрии § 1. Плоскость. Имеем OXYZ и некоторую поверхность S F ( x, y, z ) = 0 Определение 1 : уравнение с тремя переменными называется уравнением поверхности S в пространстве, если этому уравнению удовлетворяют координаты каждой точки, лежащей на поверхности и не удовлетворяют координаты ни одной точки не лежащей на ней. y z x О ( S ) 2
Слайд 3
Пример. Уравнение ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 = R 2 ( R > 0) определяем сферу с центром в точке C ( a, b, c ) и радиусом R. M ( x, y, z ) – переменная точка M ϵ ( S ) | CM | = R M C 3
Слайд 4
Определение 2 : Поверхность S называется поверхностью n -того порядка, если в некоторой декартовой системе координат она задается алгебраическим уравнением n -той степени F ( x, y, z ) = 0 (1) В примере ( S ) - окружность, поверхность второго порядка. Если S - поверхность n -того порядка, то F ( x, y, z ) - многочлен n -той степени относительно ( x, y, z ) Рассмотрим единственную поверхность 1-го порядка – плоскость. Составим уравнение плоскости проходящей через точку M 0 ( x 0, y 0, z 0 ), с вектором нормали 4
Слайд 5
Пусть M ( x, y, z ) - это произвольная (текущая) точка плоскости. или в координатной форме: Уравнение (2) - уравнение плоскости проходящей через точку М с данным вектором нормали. (2) M 0 M О α 5
Слайд 6
D (*) (3) - полное уравнение плоскости Неполное уравнение плоскости. Если в уравнении (3) несколько коэффициентов (но не A, B, C одновременно) = 0, то уравнение называется неполным и плоскость α имеет особенности в расположении. Например если D = 0, то α проходит через начало координат. 6
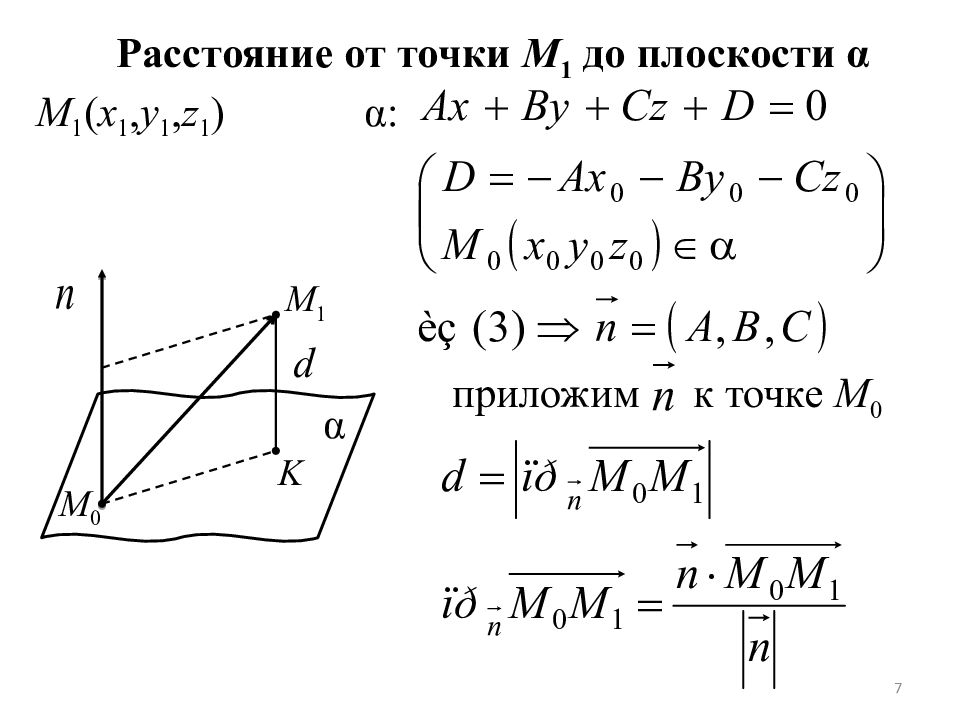
Слайд 7
Расстояние от точки М 1 до плоскости α М 1 ( x 1, y 1, z 1 ) α : приложим к точке M 0 M 0 M 1 K α 7 d
Слайд 8
- расстояние от точки M 1 до плоскости α Уравнение плоскости «в отрезках» Составим уравнение плоскости отсекающей на координатных осях ненулевые отрезки с величинами a, b, c. В качестве возьмем Составим уравнение для т. A с 8 B (0, b,0) A ( a, 0,0) C (0, 0, c )
Слайд 9
уравнение плоскости, проходящей через точку А, перпенди - кулярно вектору нормали -уравнение плоскости α " в отрезках" 9
Слайд 10
§2. Общее уравнение прямой. Прямую в пространстве можно задать пересечением 2-х плоскостей. (1) уравнение прямой Система вида (1) определяет прямую в пространстве, если коэффициенты A 1, B 1, C 1 одновременно непропорциональны A 2, B 2, C 2. 10
Слайд 11
Параметрические и канонические уравнения прямой -произвольная точка прямой 11 M 0 M точка Параметрическое уравнение t - параметр
Слайд 12
Исключив t получим: - каноническое уравнение 12 Система (3) определяет движение материальной точки, прямолинейное и равномерное из начального положения M 0 ( x 0, y 0, z 0 ) со скоростью в направлении вектора.
Слайд 14
Угол между прямыми в пространстве. Условия параллельности и перпендикулярности. Пусть в пространстве две прямые L 1, L 2 заданы своими каноническими уравнениями: Тогда задача определения угла между этими прямыми сводится к определению угла между
Слайд 15
15 их направляющими векторами: Пользуясь определением скалярного произведения и выражением в координатах указанного скалярного произведения и длин векторов q 1 и q 2, получим для нахождения :
Слайд 16
16 Условие параллельности прямых l 1 и l 2 соответствует коллинеарности q 1 и q 2, заключается в пропорциональности координат этих векторов, т.е. имеет вид: Условие перпендикулярности следует из определения скалярного произведения и его равенства нулю (при cos = 0 ) и имеет вид: l 1 l 2 + m 1 m 2 + n 1 n 2 = 0.
Слайд 17
17 Угол между прямой и плоскостью: условия параллельности и перпендикулярности прямой и плоскости Рассмотрим плоскость P, заданную общим уравнением: Ах + By + Cz + D = 0, и прямую L, заданную каноническим уравнением:
Слайд 18
18 Т.к. угол между прямой L и плоскостью П является дополнительным к углу между направляющим вектором прямой q = ( l, m, n ) и нормальным вектором плоскости n = ( А, В, С ), то из определения скалярного произведения q n = q n cos и равенства cos = sin ( = 90 - ), получим:
Слайд 19
19 Условие параллельности прямой L и плоскости П (включающее в себя принадлежность L к П ) эквивалентно условию перпендикулярности векторов q и n и выражается = 0 скалярного произведения этих векторов: q n = 0 : А l + Bm + Cn = 0. Условие перпендикулярности прямой L и плоскости П эквивалентно условию параллельности векторов n и q и выражается пропорциональностью координат этих векторов:
Слайд 20
20 Условия принадлежности двух прямых к одной плоскости Две прямые в пространстве L 1 и L 2 могут: 1) пересекаться; 2) быть параллельными; 3) скрещиваться. В первых двух случаях прямые L 1 и L 2 лежат в одной плоскости. Установим условие принадлежности к одной плоскости двух прямых, заданных каноническими уравнениями:
Слайд 21
21 Очевидно, что для принадлежности двух указанных прямых к одной плоскости необходимо и достаточно, чтобы три вектора = ( х 2 - х 1, у 2 - у 1, z 2 - z 1 ); q 1 = ( l 1, m 1, n 1 ) и q 2 = ( l 2, m 2, n 2 ), были компланарны, для чего в свою очередь необходимо и достаточно, чтобы смешанное произведение указанных трех векторов = 0.
Слайд 22
22 Записывая смешанные произведения указанных векторов в координатах получаем необходимое и достаточное условие принадлежности двух прямых L 1 и L 2 к одной плоскости:
Слайд 23
23 Условие принадлежности прямой к плоскости Пусть есть прямая и плоскость Ах + Ву + С z + D = 0. Эти условия имеют вид: Ах 1 + Ву 1 + С z 1 + D = 0 и А l + В m + С n = 0, первое из которых означает, что точка М 1 ( х 1, у 1, z 1 ), через которую проходит прямая, принадлежит плоскости, а второе – условие параллельности прямой и плоскости.
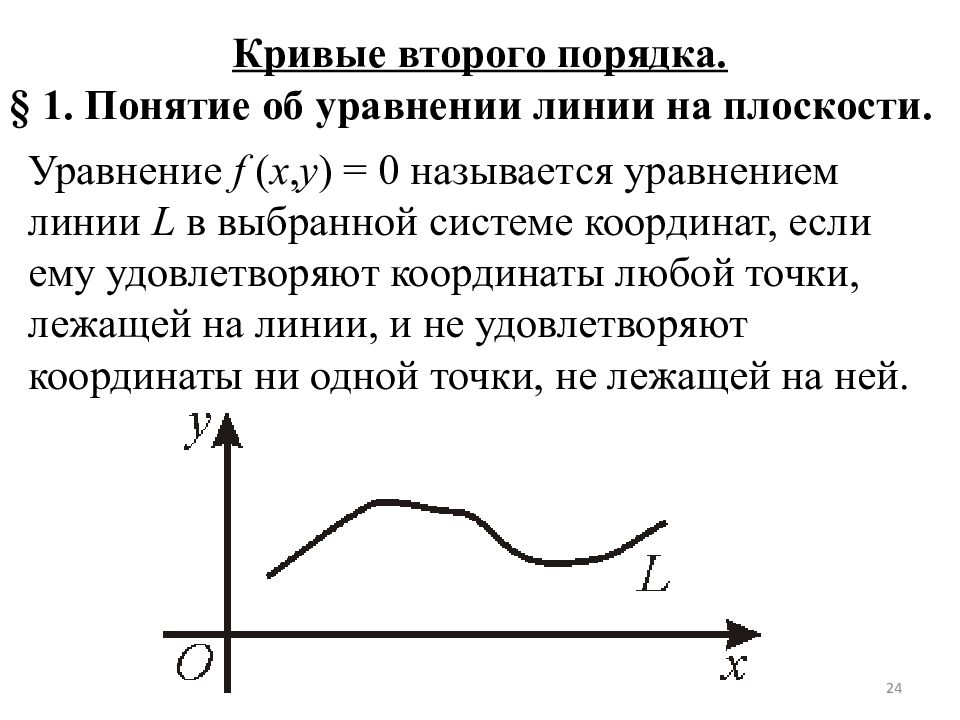
Слайд 24
Кривые второго порядка. § 1. Понятие об уравнении линии на плоскости. Уравнение f ( x, y ) = 0 называется уравнением линии L в выбранной системе координат, если ему удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней. 24
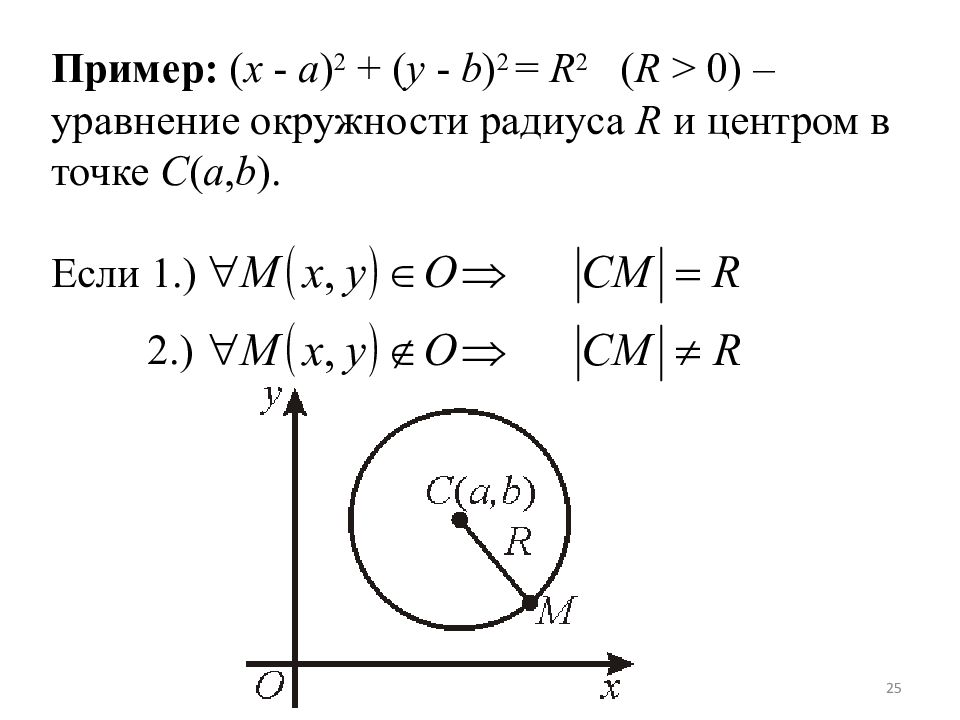
Слайд 25
25 Пример: ( x - a ) 2 + ( y - b ) 2 = R 2 ( R > 0) – уравнение окружности радиуса R и центром в точке С ( a, b ). Если 1.) 2.)
Слайд 26
Линия L называется линией n -того порядка, если в некоторой декартовой системе координат она задается алгебраическим уравнением n -той степени относительно x и y. Мы знаем единственную линию 1-го порядка – прямую: Ax + By + D = 0 Мы будем рассматривать кривые 2-го порядка: эллипс, гиперболу, параболу. Общее уравнение линий 2-ого порядка имеет вид: Ax 2 + By 2 + Cxy + Dy + Ex + F = 0 26
Слайд 27
Эллипс (Э) Определение. Эллипс – множество всех точек плоскости, сумма расстояний которых до двух фиксированных точек плоскости F 1 и F 2, называемых фокусами, есть величина постоянная и б о льшая расстояния между фокусами. Обозначим постоянную 2 а, расстояние между фокусами 2 с ( а > с, а > 0, с > 0). Проведем ось Х через фокусы, ось Y через середины фокусного расстояния. Пусть М – произвольная точка эллипса, т. М ϵ Э r 1 + r 2 = 2 a (1), где r 1, r 2 – фокальные радиусы Э. 27
Слайд 28
Запишем (1) в координатной форме: (2) Это уравнение эллипса в выбранной системе координат. Упрощая (2) получим : b 2 = a 2 - c 2 (3) – каноническое уравнение эллипса. Можно показать, что (2) и (3) эквивалентны: 28
Слайд 29
Исследование формы эллипса по каноническому уравнению 1) Эллипс – кривая 2-го порядка 2) Симметрия эллипса. т.к. x и y входят в (3) лишь в четных степенях, то эллипс имеет 2 оси и 1 центр симметрии, которые в выбранной системе координат совпадают с выбранными осями координат и точкой О. 29
Слайд 30
3) Расположение эллипса Т.е. весь Э расположен внутри прямоугольника, стороны которого x = ± a и y = ± b. 4) Пересечение с осями. С ОХ : С ОУ : В силу симметрии эллипса рассмотрим его поведение ( ↑↓ ) лишь в I четверти. A 1 (- a ;0); A 2 ( a ;0); вершины эллипса B 1 ( 0 ; b ); B 2 (0;- b ); 30
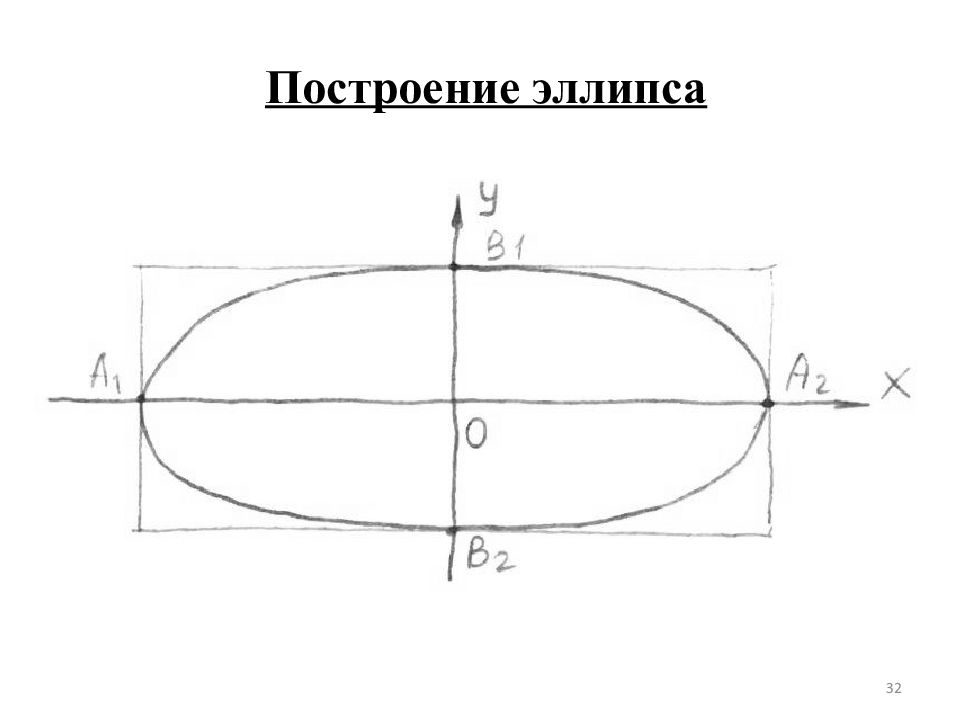
Слайд 31
Разрешив (3) относительно y получим: в I четверти x > 0 и эллипс убывает. Вывод: Э – замкнутая кривая, овальная, имеющая четыре вершины. План построения Э. 1) Строим прямоугольник со сторонами 2 a, 2 b 2) Вписываем выпуклую овальную линию 31
Слайд 33
Гипербола (Г) Определение : Г – множество всех точек плоскости, модуль разности расстояний которых до 2-х фиксированных точек плоскости F 1, F 2 есть величина постоянная и < этого расстояния. 2 а, | F 1 F 2 | = 2 c Выберем систему координат. точка М ϵ Г | r 1 - r 2 |= 2 a r 1 - r 2 = ± 2 а В координатной форме: (1) – уравнение Г в выбранной системе координат 33
Слайд 34
Упрощая (1): (2) – каноническое уравнение Г. и (2) – эквивалентны. Исследование гиперболы по каноническому уравнению 1) Г- линия 2-го порядка 2) Г имеет две оси и один центр симметрии, которые в нашем случае совпадают с координатными осями и началом координат. 3) Расположение гиперболы. 34
Слайд 35
Гипербола расположена вне полосы между прямыми x = a, x = - a. 4) Точки пересечения с осями. OX : OY : не имеет решений A 1 (- a ;0); A 2 ( a ;0) – действительные вершины Г B 1 ( 0 ; b ); B 2 (0;- b ) – мнимые вершины Г 2 a – действительная ось Г 2 b – мнимая ось Г 35
Слайд 36
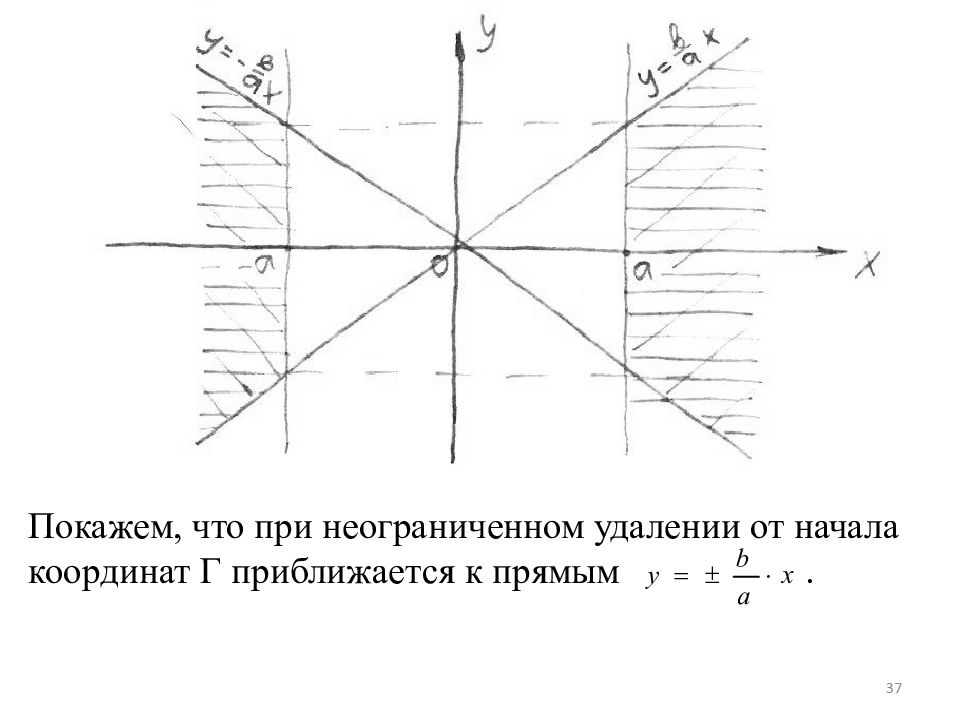
5) Асимптоты гиперболы. В силу симметрии Г рассмотрим ее часть в I четверти. Разрешив (2) относительно y, получим: уравнение Г в I четверти x ≥ 0 Рассмотрим прямую: т.к. в I четверти x >0, то т.е. в I четверти при одной и той же абсциссе, ордината прямой > ординаты соответствующей точки Г, т.е. в I четверти Г лежит ниже этой прямой. Вся Г лежит внутри вертикального угла со сторонами 36
Слайд 37
Покажем, что при неограниченном удалении от начала координат Г приближается к прямым. 37
Слайд 38
6) Можно показать, что в I ч. Г возрастает 7) План построения Г а) строим прямоугольник 2 a, 2 b б) проводим его диагонали в) отметим А 1, А 2 – действительные вершины Г и впишем эти ветви 38
Слайд 39
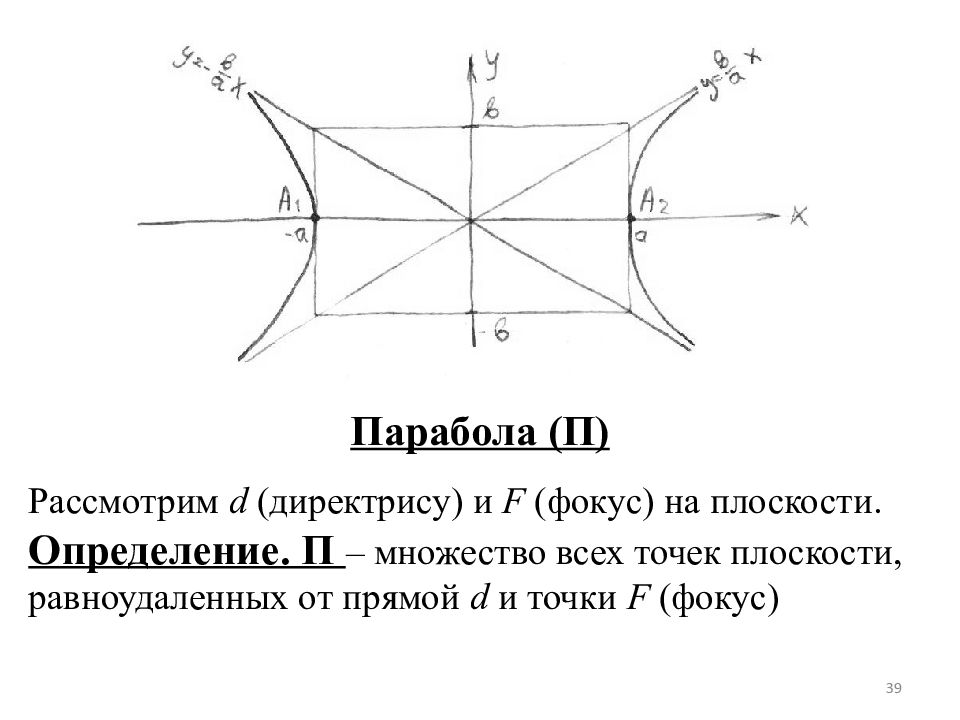
Парабола (П) Рассмотрим d ( директрису ) и F ( фокус ) на плоскости. Определение. П – множество всех точек плоскости, равноудаленных от прямой d и точки F ( фокус ) 39
Слайд 40
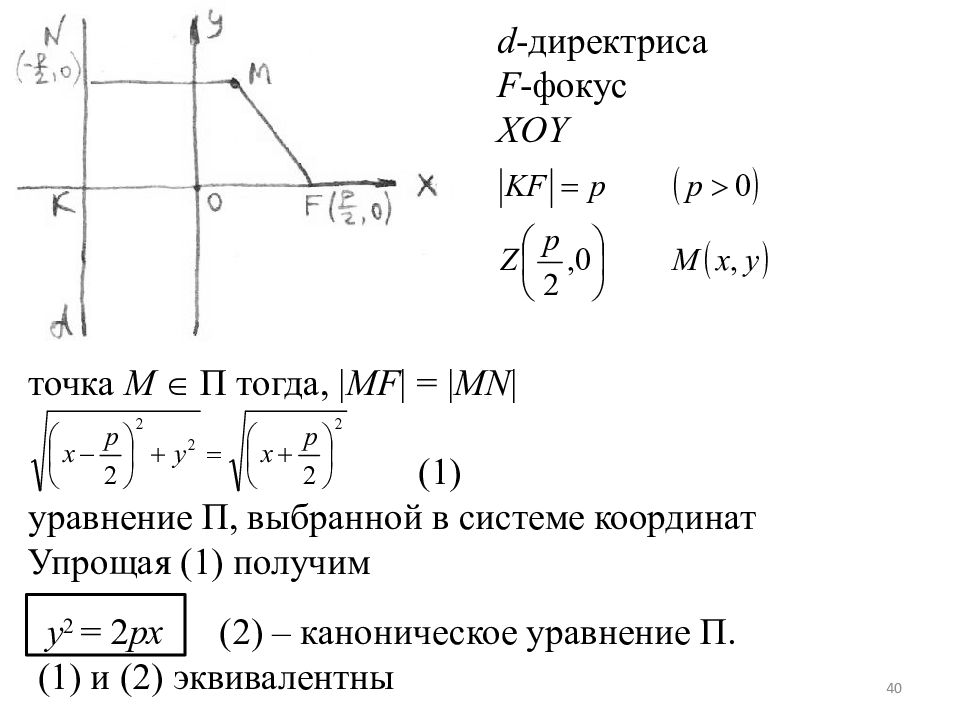
d - директриса F - фокус XOY точка М П тогда, | MF | = | MN | (1) уравнение П, выбранной в системе координат Упрощая (1) получим y 2 = 2 px (2) – каноническое уравнение П. (1) и (2) эквивалентны 40
Слайд 41
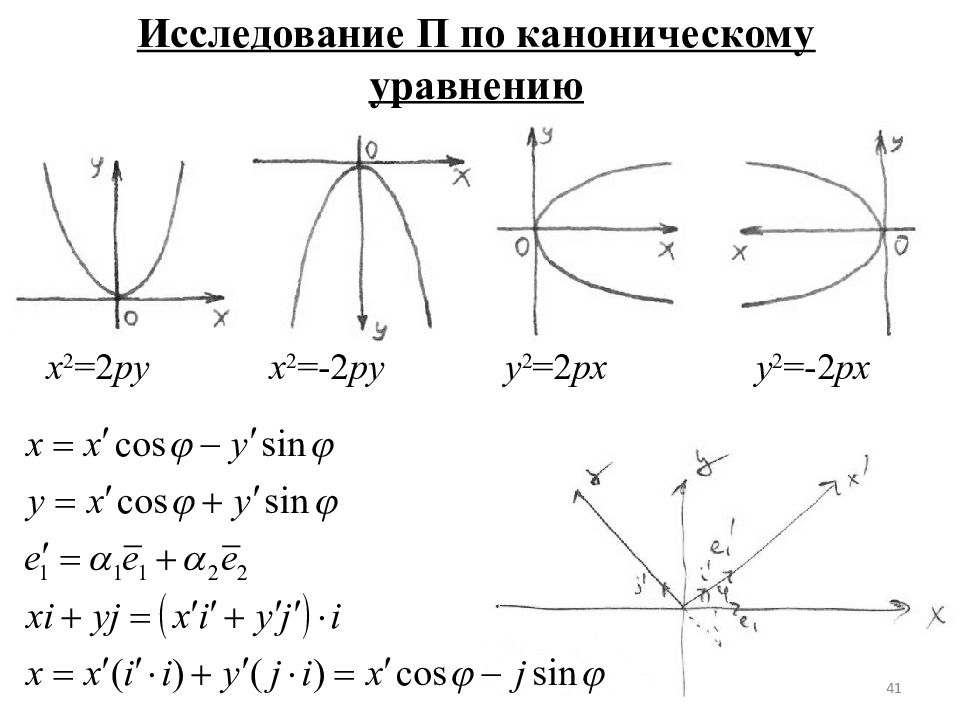
Исследование П по каноническому уравнению x 2 =2 py x 2 =-2 py y 2 =2 px y 2 =-2 px 41
Слайд 42
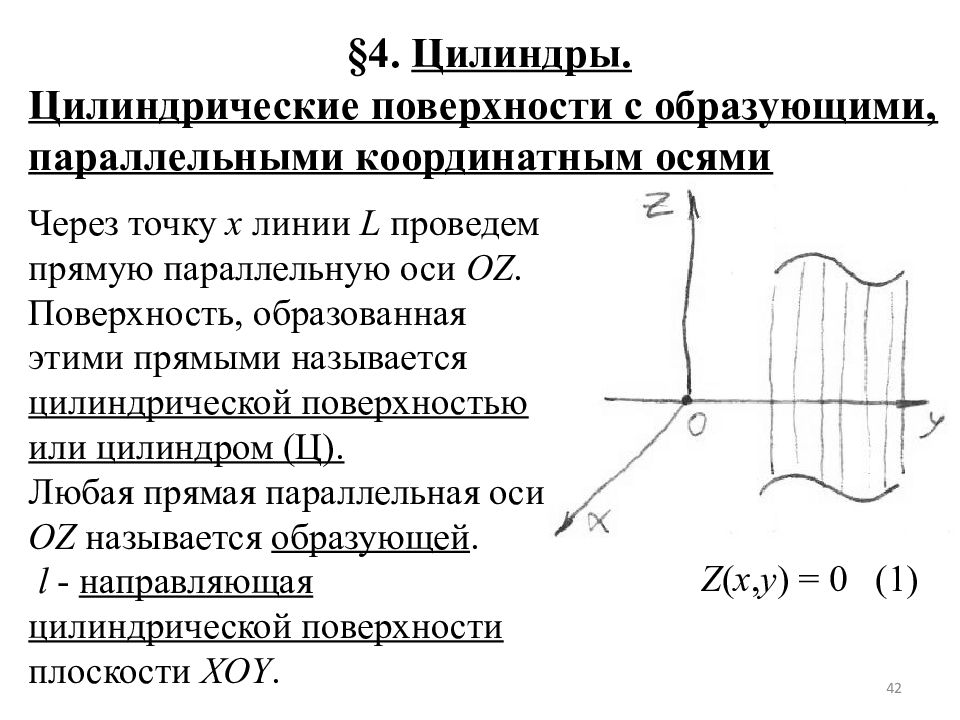
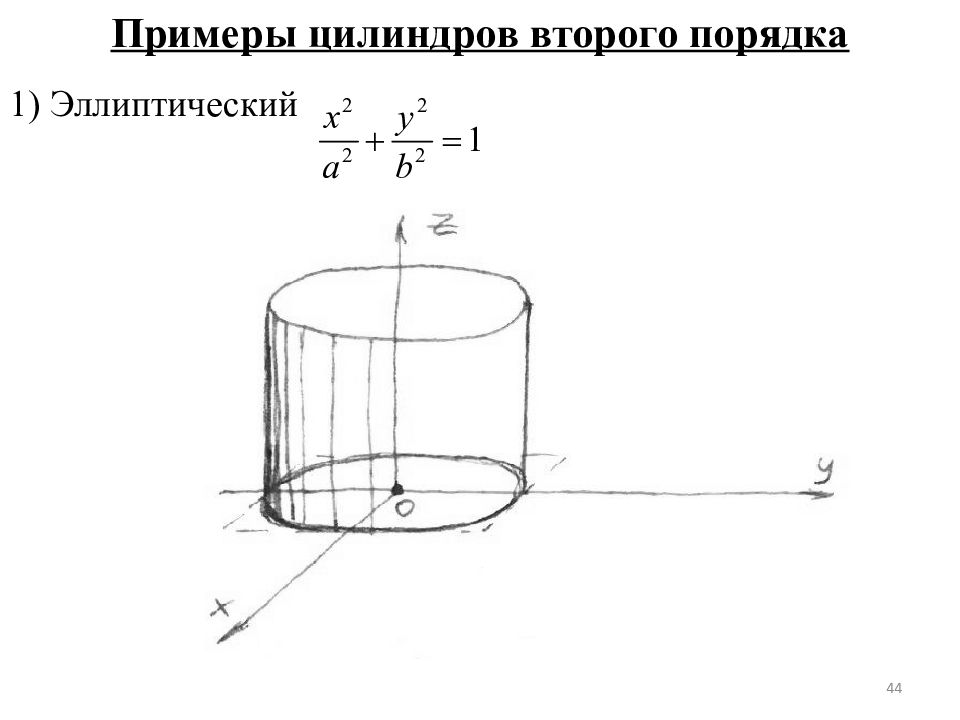
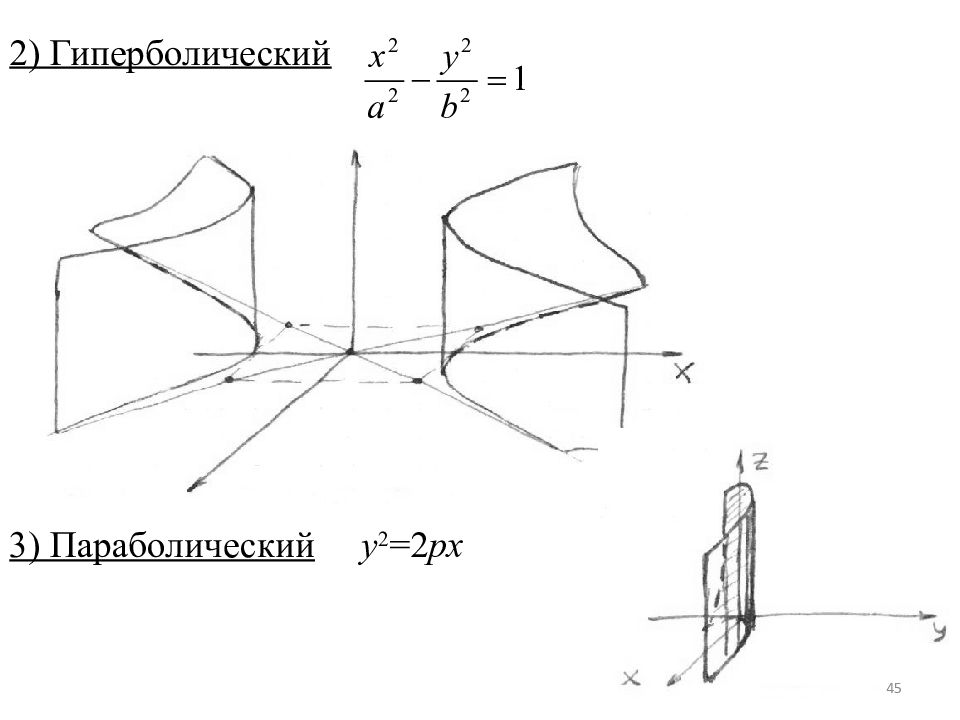
§ 4. Цилиндры. Цилиндрические поверхности с образующими, параллельными координатным осями Через точку х линии L проведем прямую параллельную оси OZ. Поверхность, образованная этими прямыми называется цилиндрической поверхностью или цилиндром (Ц). Любая прямая параллельная оси OZ называется образующей. l - направляющая цилиндрической поверхности плоскости XOY. Z ( x, y ) = 0 (1) 42
Слайд 43
Пусть М ( x, y, z ) – произвольная точка цилиндрической повер-хности. Спроецируем ее на L. M 0 ϵ L => Z ( x 0, y 0 ) = 0 (2) x = x 0 y = y 0 => Z ( x, y ) = 0 M ϵ Ц M 0 ϵ L то есть координаты М удовлетворяют (1) очевидно, что если М Ц, то она не проектируется в точку М 0 ϵ L и следовательно, координаты М не будут удовлетворять уравнению (1), которое определяет Ц с образующей параллельной оси OZ в пространстве. Аналогично можно показать, что : Ф( x, z ) = 0 в пространстве Ц || OY ( y, z ) = 0 определяет в пространстве Ц || OX 43
Слайд 46
Проекция пространственной линии на координатной плоскости Линию в пространстве можно задать параметрически и пересечением поверхностей. Одну и ту же линию можно задать ∩ различных поверхностей. Пусть пространственная линия L задается ∩ двух поверхностей α : S 1 : Ф 1 ( x, y, z ) = 0 S 2 : Ф 2 ( x, y, z ) = 0 уравнение L Ф 1 ( x, y, z ) = 0 (1) Ф 2 ( x, y, z ) = 0 Найдем проекцию L на плоскость XOY из уравнения (1) исключаем Z. Получим уравнение: Z ( x, y ) = 0 – в пространстве это уравнение Ц с образующей || OZ и направляющей L. 46
Слайд 47
Проекция: L xy Z ( x, y ) = 0 Z = 0 Поверхности второго порядка Эллипсоид – каноническое уравнение поверхности имеет вид: 1) Эллипсоид – поверхность второго порядка. 2) X, Y, Z входят в уравнение лишь в четных степенях = > поверхность имеет 3 плоскости и 1 центр симметрии, которые в выбранной системе координат совпадают с координатными плоскостями и началом координат. 47
Слайд 48
3) Расположение эллипсоида Поверхность заключена между || плоскостями с уравнениями x = a, x = - a. Аналогично т.е. вся поверхность заключена внутри прямоугольного параллелепипеда. х = ± а, y = ± b, z = ± с. Будем исследовать поверхность методом сечений – пересекая поверхность координатными плоскостями и плоскостями || координатным. В сечении будем получать линии, по форме которых будем судить о форме поверхности. 48
Слайд 49
Пересечем поверхность плоскостью XOY. В сечении получим линию. Аналогично с плоскостью YOZ Плоскость || XOY Если h ( 0, с ), то оси эллипса убывают от a и b до 0. -эллипс с полуосями b и с - эллипс a и b – полуоси 49
Слайд 50
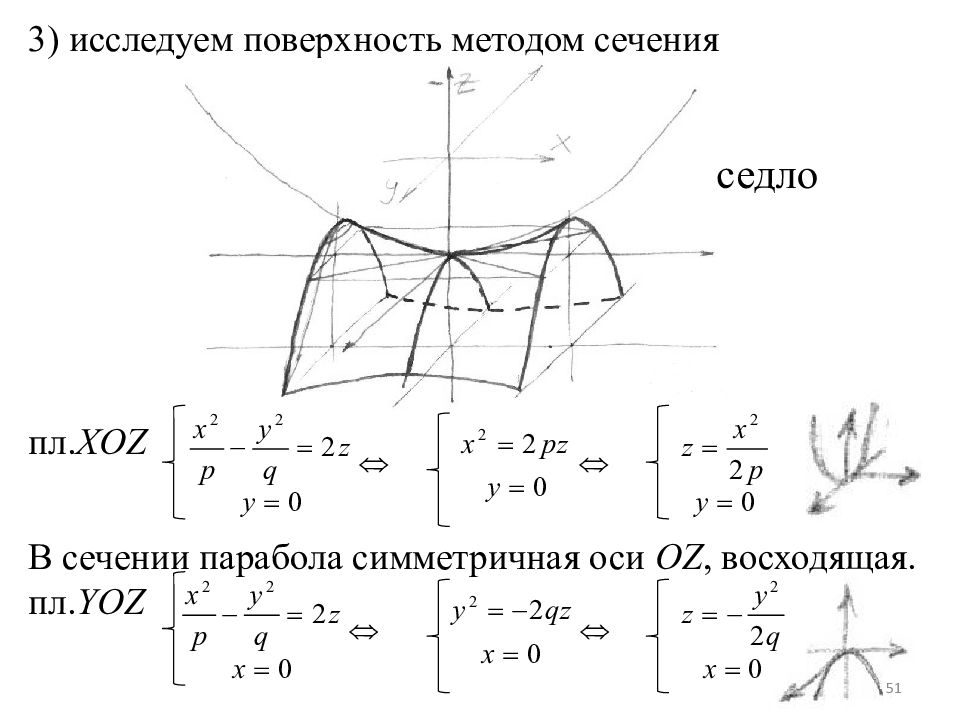
a = b = с - сфера Параболоиды а) Гиперболический параболоид – поверхность с каноническим уравнением: 1) Поверхность второго порядка 2) Так как x, y входят в уравнение лишь в четных степенях, то поверхность имеет плоскости симметрии, которые при данном выборе координат совпадают с плоскостями XOZ, YOZ. 50
Слайд 51
3 ) исследуем поверхность методом сечения пл. XOZ В сечении парабола симметричная оси OZ, восходящая. пл. YOZ седло 51
Слайд 52
пл. || YOZ пл. || XOZ пл. XOY В сечении пара прямых, проходящих через начало координат 52
Слайд 53
пл. || XOY при h > 0 гиперболы, с действительной полуосью вдоль OX, при h < 0 гиперболы, с действительной полуосью вдоль оси Y. Эллиптический параболоид 1) поверхность второго порядка 2) имеет 2 плоскости симметрии, которые совпадают с XOZ и YOZ 3) левая часть уравнения неотрицательна = > z ≥ 0, то есть, вся поверхность расположена над XOY. 4) исследуем поверхность методом сечения 53
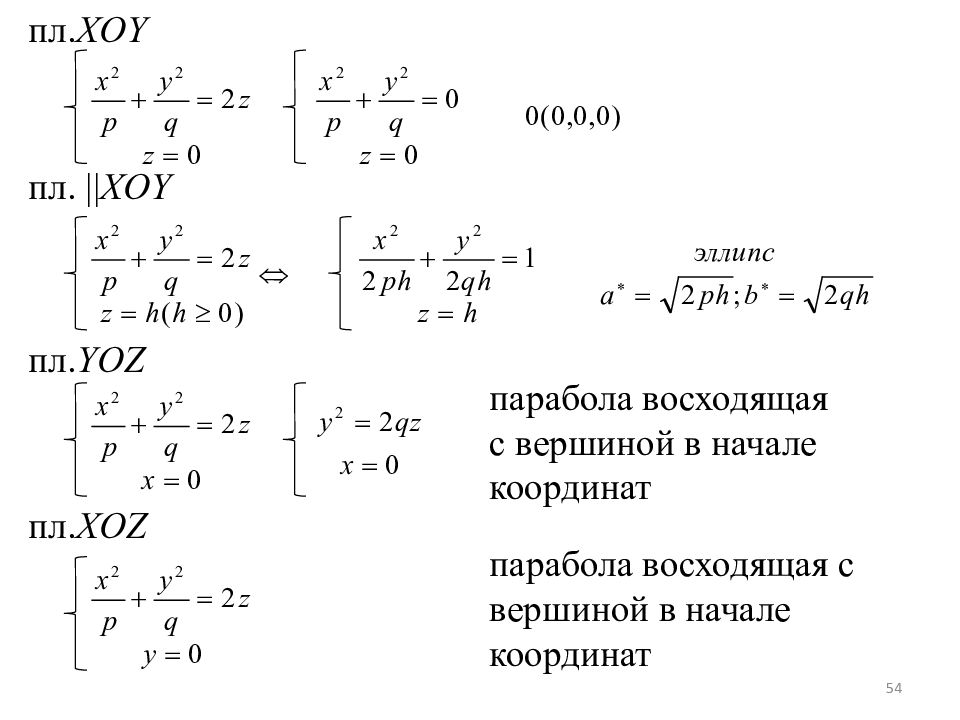
Слайд 54
пл. XOY пл. || XOY пл. YOZ пл. XOZ парабола восходящая с вершиной в начале координат парабола восходящая с вершиной в начале координат 54
Слайд 55
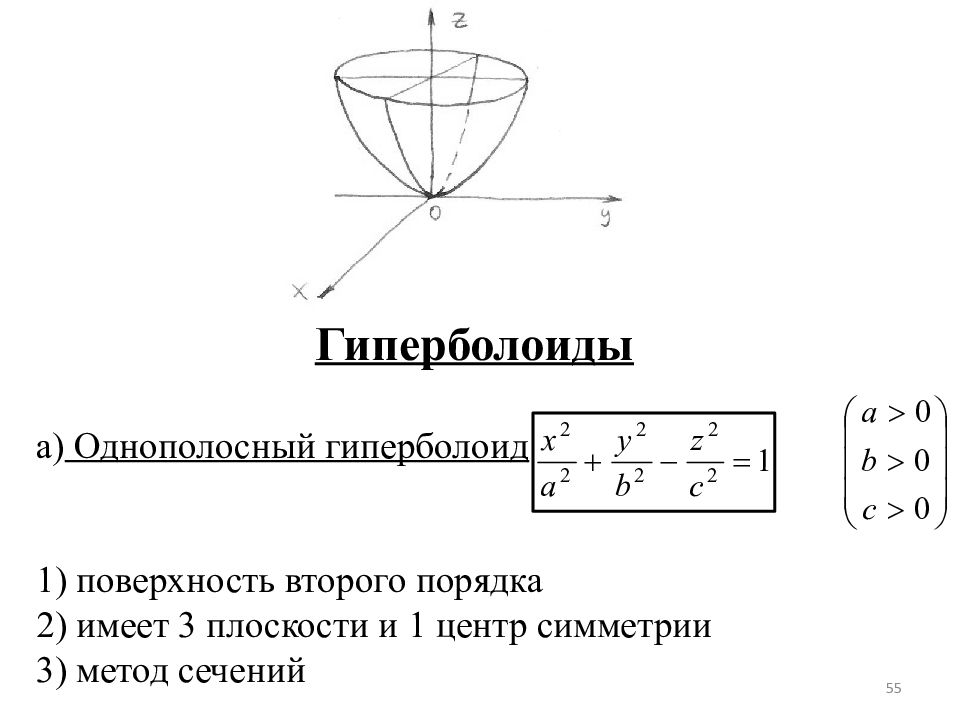
Гиперболоиды а) Однополосный гиперболоид 1) поверхность второго порядка 2) имеет 3 плоскости и 1 центр симметрии 3) метод сечений 55
Слайд 56
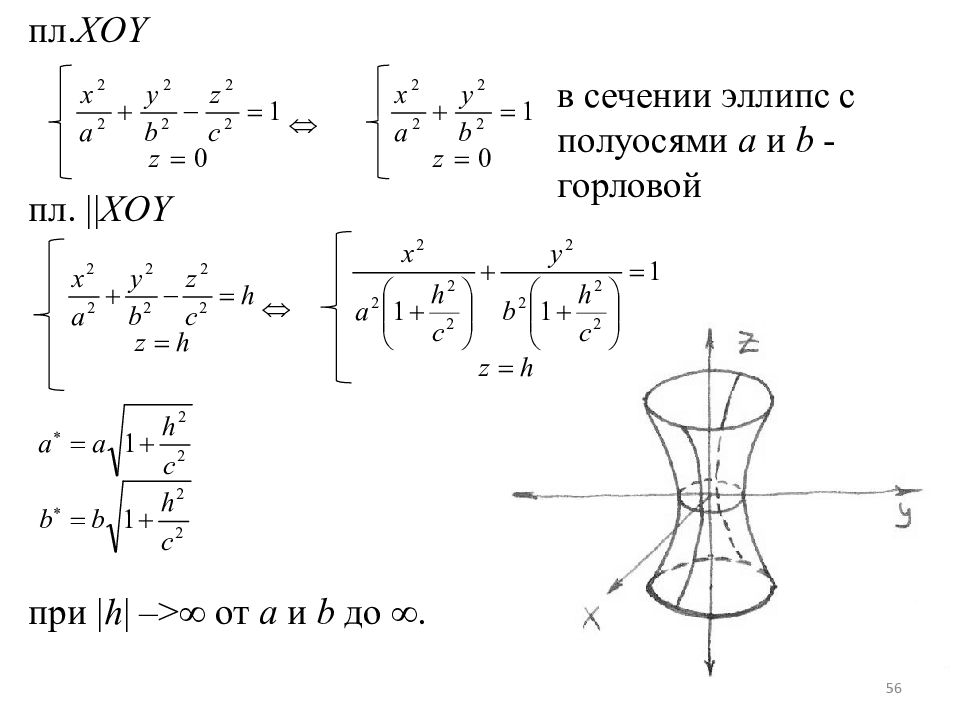
пл. XOY пл. || XOY при | h | – >∞ от a и b до ∞. 56 в сечении эллипс с полуосями а и b - горловой
Слайд 57
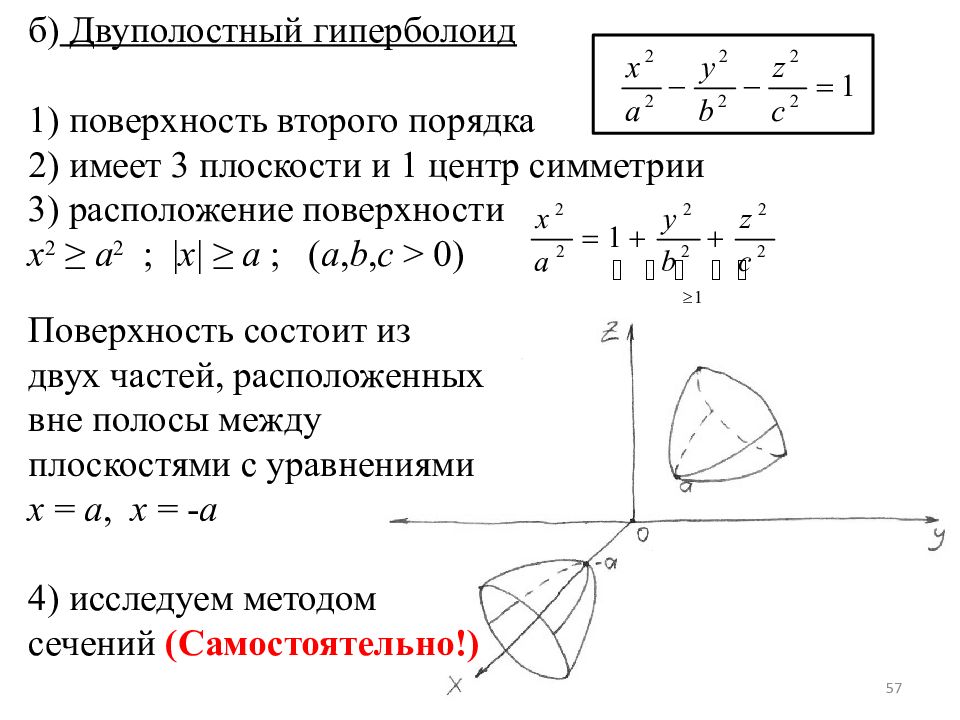
б) Двуполостный гиперболоид 1) поверхность второго порядка 2) имеет 3 плоскости и 1 центр симметрии 3) расположение поверхности x 2 ≥ a 2 ; | x | ≥ a ; ( a, b, c > 0) Поверхность состоит из двух частей, расположенных вне полосы между плоскостями с уравнениями x = a, x = - a 4) исследуем методом сечений (Самостоятельно!) 57
Слайд 58
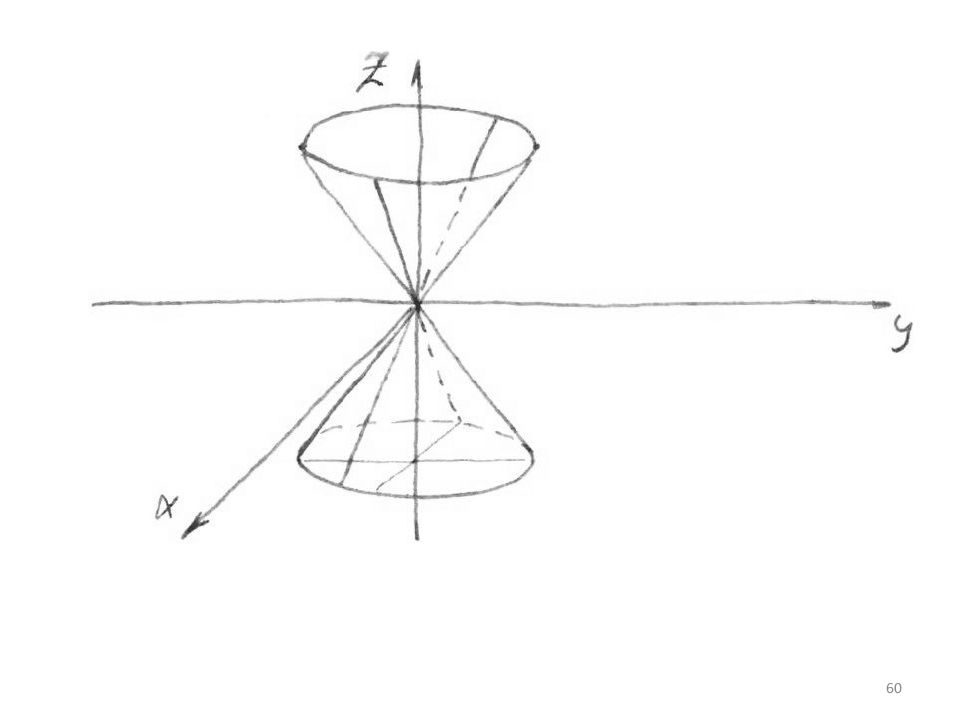
Конус второго порядка Конусом второго порядка называется поверхность, каноническое уравнение которой имеет вид: 1) поверхность второго порядка 2) имеет 3 плоскости и 1 центр симметрии 3) исследуем методом сечений пл. XOY 58
Слайд 59
пл. || XOY | h | – >∞ от 0 до ∞ пл. YOZ пара прямых, проходящих через начало координат пл. XOZ пара прямых, проходящих через начало координат 59