Контрольная работа (домашняя) по методичке 15876 (с.27 ), задачи 3,4,5( а,б,в ) Практикумы «Алгебра» и « Матем.анализ » Солдатова Гульнара Тагировна gulnara.soldatova@yandex.ru
РАЗДЕЛ 1. Элементы линейной (задача 3) РАЗДЕЛ 2. Элементы математического анализа (задачи 4-5)
§ 1. Матрицы. Операции над ними. § 2. Определители. §3. Обратная матрица § 4. Решение СЛАУ.
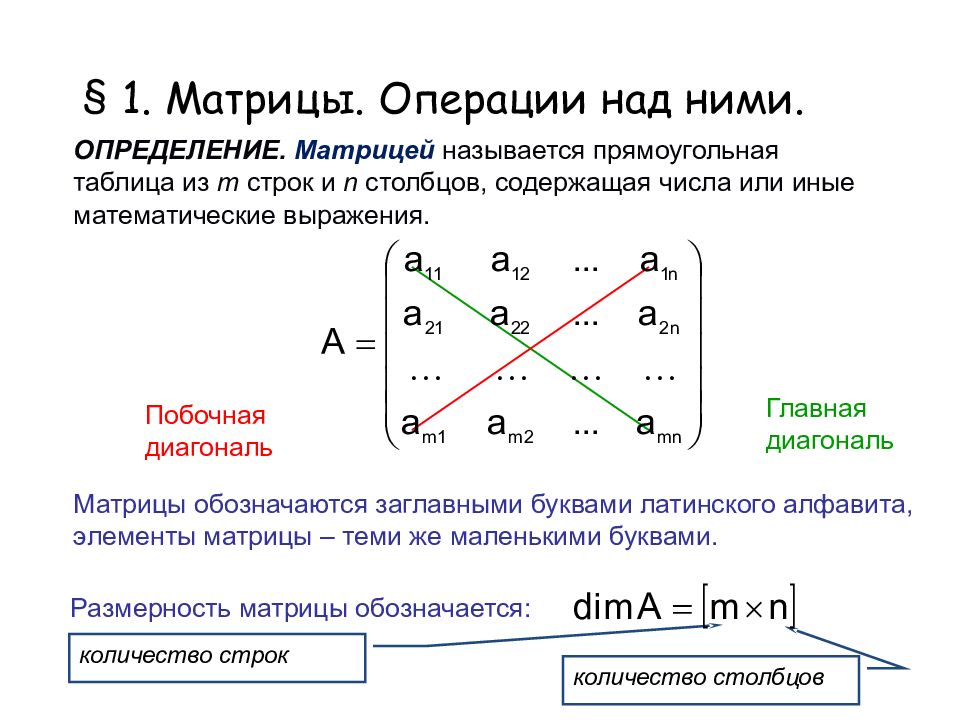
ОПРЕДЕЛЕНИЕ. Матрицей называется прямоугольная таблица из m строк и n столбцов, содержащая числа или иные математические выражения. Матрицы обозначаются заглавными буквами латинского алфавита, элементы матрицы – теми же маленькими буквами. Размерность матрицы обозначается: количество строк количество столбцов Главная диагональ Побочная диагональ § 1. Матрицы. Операции над ними.
1) Если, то матрица называется прямоугольн ой. 2) Если, то матрица называется квадратной ( n - ного порядка ). 3) Матрица типа называется вектор-строк ой: Матрица типа называется вектор-столбцом :
4) Квадратная матриц а называется единичной, если ее элементы, расположенные на главной диагонали, равны единице, остальные – нулю (обозначается буквой Е ): 5) Если все элементы матрицы равны нулю, то она называется нул евой матрицей и обозначается символом 0.
6) Квадратная матрица называется диагональной, если элементы, стоящие вне главной диагонали равны нулю 7) Квадратная матрица называется треугольной, если элементы, стоящие ниже (выше) главной диагонали равны нулю:
Равенство матриц Сложение (вычитание) матриц Сумма и разность матриц существуют только для матриц одинакового размера, при этом соответствующие элементы матриц складываются или вычитаются. Матрицы равны, если они имеют одинаковую размерность и их соответствующие элементы равны. Транспонирование матрицы Операция получения из данной матрицы транспонированной заменой каждой строки столбцом с тем же номером
Умножение матрицы на число Найти значение выражения: При умножении матрицы A на число k получается матрица того же размера, при этом каждый элемент матрицы A умножается на k. Решение:
Умножение матриц Произведение матриц A * B определено только тогда, когда число столбцов матрицы А равно числу строк матрицы В, в противном случае произведение не существует. Пример 1. Пример 2.
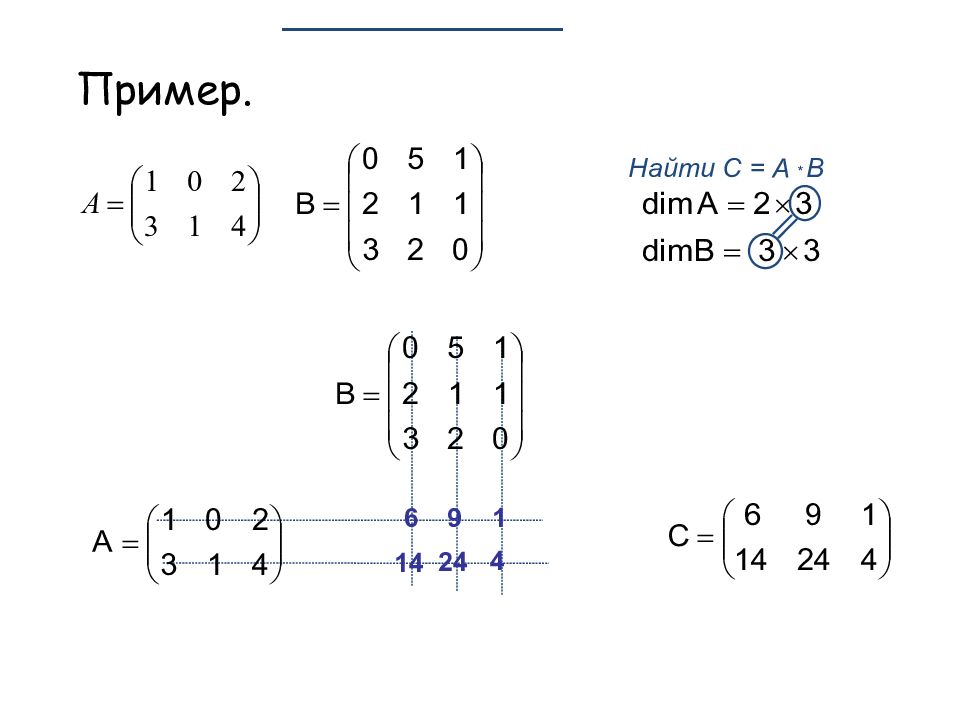
Произведением матрицы A размера с элементами a i j на матрицу B размера с элементами b j q называется матрица C р азмера с элементами :
Найти С = A * B 6 9 1 14 24 4
Найти произведение матриц АВ и проверить, перестановочны ли матрицы Решение:
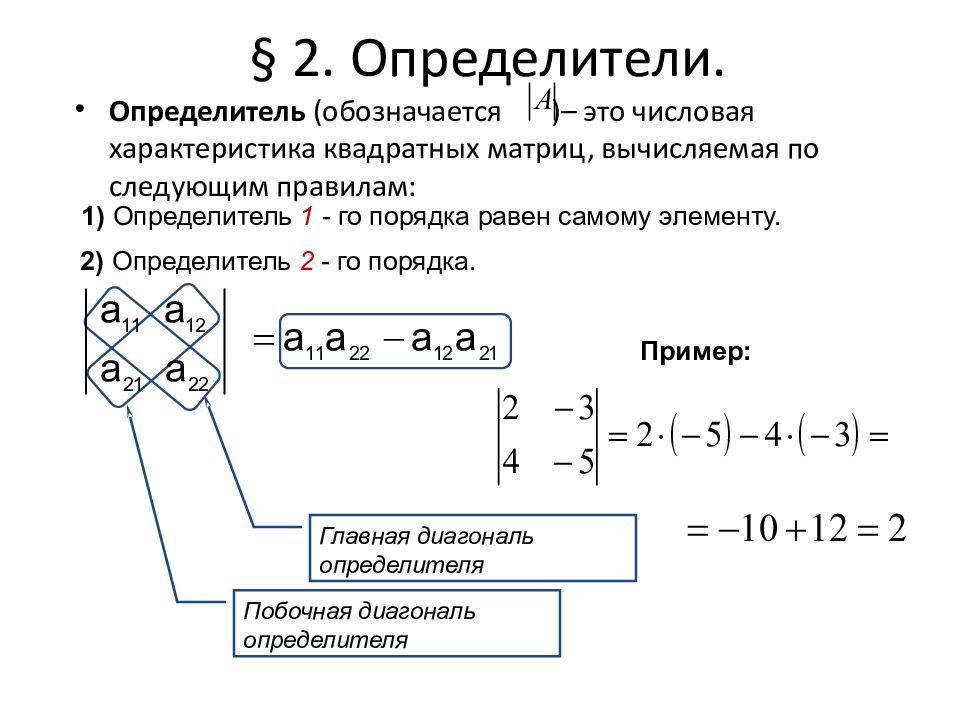
2) Определитель 2 - го порядка. Главная диагональ определителя Побочная диагональ определителя § 2. Определители. Определитель (обозначается )– это числовая характеристика квадратных матриц, вычисляемая по следующим правилам: 1) Определитель 1 - го порядка равен самому элементу. Пример:
a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 - - ( a 13 a 22 a 31 + a 21 a 12 a 33 + a 32 a 23 a 11 «+» «-» 3) Определитель 3 - го порядка. Правило треугольников. )
Метод треугольника применим только для определителей 3 порядка Пример.
Свойства определителя произвольного порядка : 1. Определитель матрицы А равен определителю транспонированной матрицы, т.е. 2. Если все элементы некоторой строки матрицы А равны 0, то определитель равен 0. 3. Общий множитель всех элементов строки определителя можно вынести за знак этого определителя. 4. Если в определителе поменять местами две строки, то он изменит знак на противоположный. 5. Если определитель имеет две равные строки, то он равен 0.
7. Значение определителя не изменится, если к элементам его некоторой строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число k. 6. Если элементы двух строк определителя пропорциональны, то определитель равен 0.
Теорема. О братная матрица существует и единственна тогда и только тогда, когда. Определение. Квадратная матрица А -1 называется о братной матрицей по отношению к квадратной матрице A n - ного порядка, если выполняется условие: АА -1 =А -1 А=Е, где A, А -1, Е – одного порядка.
Где - алгебраическое дополнение элемент а a i j вычисляется по формуле M i j - минор элемента a i j - это oпределитель, который получается из определителя n - го порядка путем вычеркивания i - й строки и j - го столбца, т.е. строки и столбца, на пересечении которых стоит элемент a i j
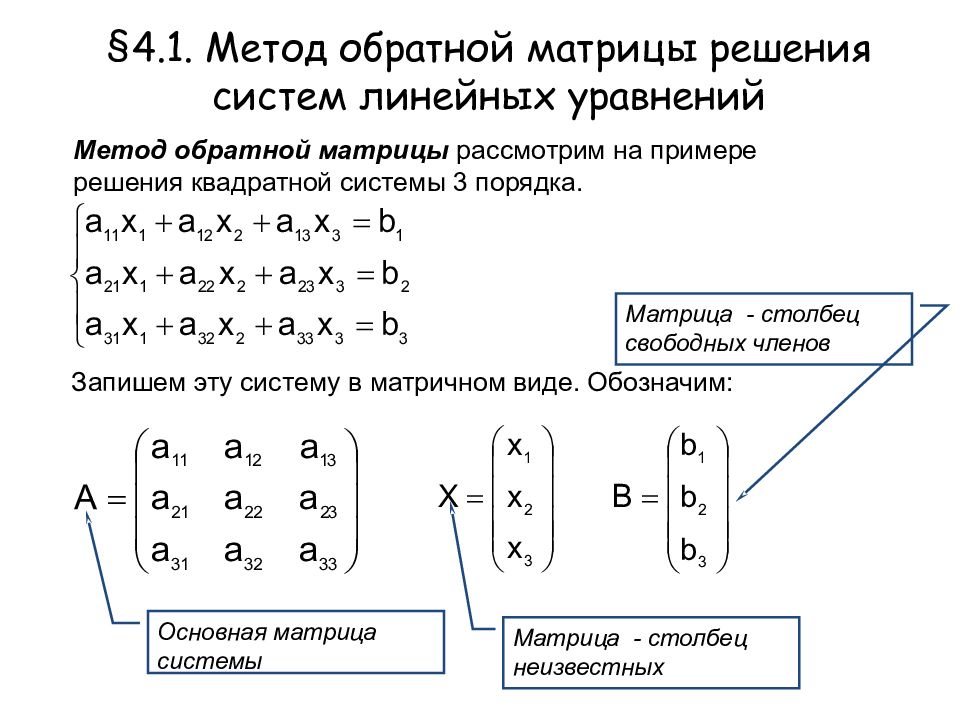
Метод обратной матрицы рассмотрим на примере решения квадратной системы 3 порядка. Запишем эту систему в матричном виде. Обозначим: Основная матрица системы Матрица - столбец неизвестных Матрица - столбец свободных членов
Тогда систему можно записать так: Найдем решение системы в матричном виде:
Решить систему методом обратной матрицы. -0,5 2 -5
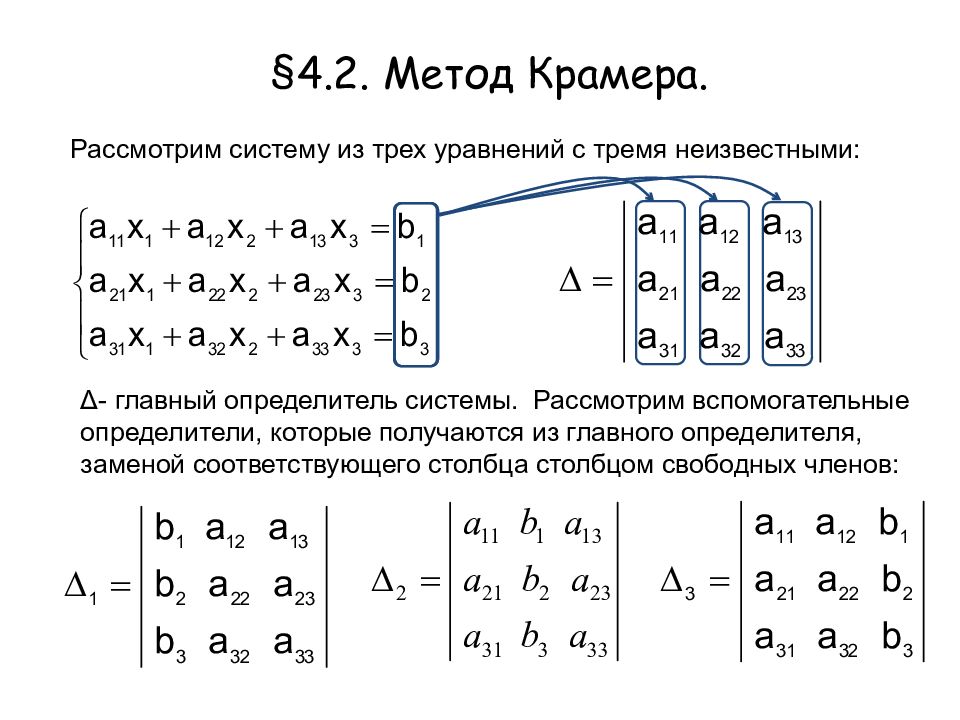
Рассмотрим систему из трех уравнений с тремя неизвестными: Δ - главный определитель системы. Рассмотрим вспомогательные определители, которые получаются из главного определителя, заменой соответствующего столбца столбцом свободных членов:
Тогда, если, система линейных уравнение имеет единственное решение, определяемое по формулам Крамера : Пусть - определитель матрицы системы А, -определитель, полученный из заменой j - го столбца столбцом свободных членов В. Или в общем случае, для системы из n уравнений с n неизвестными:
Пример : Решить систему уравнений по формулам Крамера. значит система имеет единственное решение, определяемое формулами Крамера
Рассмотрим систему линейных уравнений где числа а 11, а 12,… а 33 – коэффициенты системы, b 1, b 2, b 3 - свободные члены системы, х 1, х 2, х 3 - неизвестные. Расширенная матрица системы
Следующие действия над расширенной матрицей системы называются элементарными преобразованиями. У множение или деление элементов строк на одно и то же число, не равное нулю Перестановка местами двух строк Прибавление к элементам строки элементов другой строки, умноженных на произвольный множитель. Суть метода : с помощью элементарных преобразований над строками расширенная матрица приводится к треугольному виду.
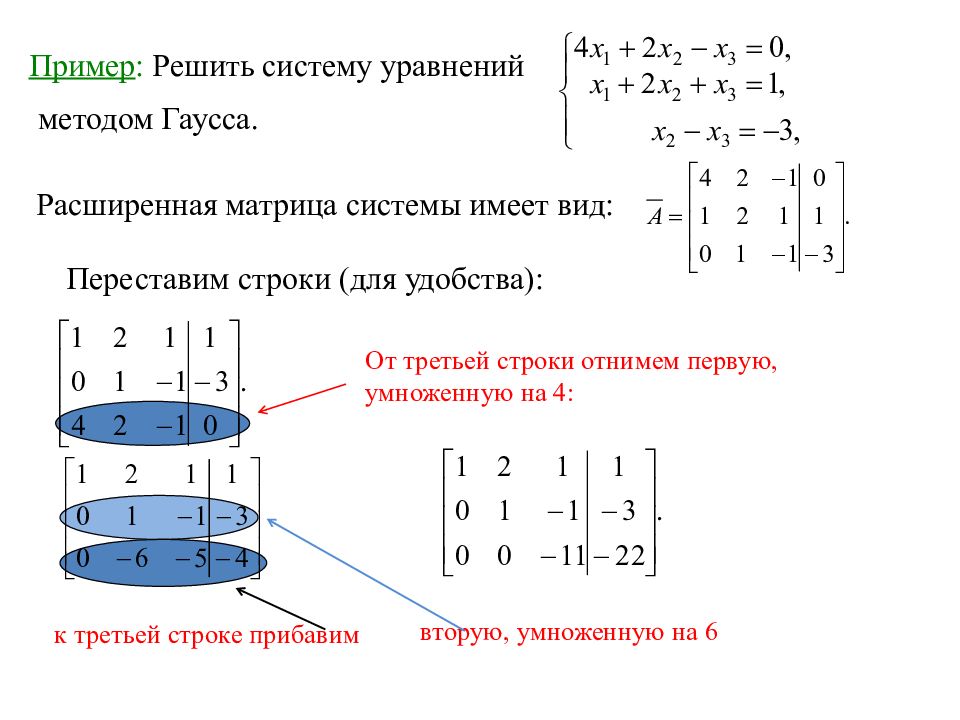
Пример : Решить систему уравнений методом Гаусса. Расширенная матрица системы имеет вид: Переставим строки (для удобства): От третьей строки отнимем первую, умноженную на 4: к третьей строке прибавим вторую, умноженную на 6
Матрица приведена к треугольному виду, ей соответствует преобразованная система уравнений: Находим решение этой системы, начиная с последнего уравнения: третью строку разделим на (-11)
