Первый слайд презентации: ЭЛЕКТРОТЕХНИКА
Лектор Доцент кафедры Электротехника К.т.н. Поляков Сергей Владимирович
Слайд 2: ЛИТЕРАТУРА
Атабеков Г.И. Теоретические основы электротехники. Ч. I. Линейные электрические цепи. М.: Энергия. 1978. 529 с. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: Учебник. – 10-е изд. – М.: 2002. –638 с.: ил. Касаткин А.С., Немцов М.В. Электротехника. Учеб. для вузов. – 6-е изд. перераб. – М.:Высш. шк., 2000. – 542 с.: ил. Нейман Л.Р., Демирчан К.С. Теоретические основы электротехники, Ч. I, II. – М.: Энергия, 1981. Попов В.П. Основы теории цепей: Учеб. для вузов. – 3-е изд., испр. – М.: Высш. шк., 2000 – 575 с.: ил. Теоретические основы электротехники / Под ред. П. А. Ионкина. Ч I, II. – М.: Высш. шк., 1975.
1.1. Электрический ток Электрический ток - это явление направленного движения свободных носителей электрического заряда.. направление, обратное направлению движения электронов, и было выбрано в качестве положительного направления электрического тока в приемнике, т.е. от «плюса» к «минусу». Численно ток определяется как предел отношения количества электричества, переносимого заряженными частицами через поперечное сечение проводника за некоторый промежуток времени t при. (1.2) где – сумма положительных и отрицательных зарядов, переносимых в противоположные стороны через рассматриваемое поперечное сечение проводника. Ток измеряется в амперах [ А ].
Слайд 4
1.2. Напряжение Электрический потенциал точки электрического поля – это работа, совершаемая силами поля при переносе единичного положительного заряда из данной точки поля в бесконечность. Единица измерения - [ В ольт] Напряжение – величина численно равная работе, совершаемой электрическим полем при переносе единичного положительного заряда из точки а в точку b. Единица измере-ния – [ В ольт ]. Для участка цепи (рис.1.1) напряжение между точками a и b может быть определено, как разность потенциалов a и b. а i b Рис.1.1. u ab (1.3) (1.4)
Слайд 5
1.3. Мощность и энергия При перемещении по участку электрической цепи элементарного электрического заряда dq под действием напряжения U силами электри-ческого поля совершается работа. Единица измерения – [ Дж оуль] положительной (при совпадающих по направлению U и i ) или отрицательной (если направления U и i противоположны). В первом случае ( P > 0 ) элемент электрической цепи потребляет энергию (является приемником), во втором ( P < 0 ) – отдает энергию (является источ ником). Энергия, поступившая в приемник за время от t 1 до t 2, определяется и измеряется в джоулях [ Дж ]. (1.5) Учитывая, что, получим Мощность Единица измерения – [ В а т т]. Мощность Р величина алгебраическая и может быть (1.6) (1.7)
Слайд 6
1.4. Пассивные и активные элементы электрической цепи 1.4.1. Резистор. Сопротивление электрическое Резистором называется элемент электричес-кой цепи, в котором происходит необратимое преобразование электрической энергии в тепловую. R.. iuРис.1.2 . а i b Рис.1. 2. u R Условное изображение резистора приведено на рис.1.2. Электрическая энергия, поступающая в резистор R за время t и превращающаяся в тепло (1.8) (1.9) Эта формула определяет закон Ома, установленный в 1826г. Величина сопротивления измеряется в омах [Ом]. Величину обратную сопротивлению называют прово-димостью. Размерность проводимости – [ С и м менс] Мощность, поступающая на резистор (1.10)
Слайд 7
1.4.2. Индуктивность. Катушка индуктивности Индуктивная катушка - элемент электрической цепи, способный накапливать энергию магнитного поля. Потокосцеплением называется сумма маг-нитных потоков ( k ), сцепленных (пронизываю-щих) с определенным числом витков k. Индуктивность всегда больше нуля и измеряется в генри [ Гн ]. По закону электромагнитной индукции изме-нение потокосцепления пронизывающего витки катушки индуктивности вызывает появление в ней электродвижущей силы (ЭДС) Падением напряжения на катушке индуктив-ности называется величина Положительное направление u L совпадает по направлению с положительным направлением i. (1.13) (1.12) (1.14) (1.15)
Слайд 8
На рис.1.3 приведено условное обозначе-ние элемента индуктивности и положитель-ного направления тока i, падения напряжения U L и ЭДС самоиндукции e L Мгновенная мощность, поступающая в катушку индуктивности, равна (1.16) Мощность связана с процессом изменения энергии магнитного поля. Рис.1.3. e L L U L .. i (1.16) Энергия, накопленная в магнитном поле катушки индуктивности, начиная с момента времени t = 0 при i = 0 (1.17)
Слайд 9
1.4.3. Емкость. Конденсатор Конденсатор – элемент электрической цепи, способный накапливать энергию в электрическом поле. Конденсатор характеризуется емкостью. Емкость - отношения заряда q к напряжению на этом элементе. Емкость измеряется в фарадах ( Ф ), причем емкость всегда больше нуля. (1.18) Ток – производная заряда во времени, отсюда (1.19) проинтегрировав (1.20) или (1.21)
Слайд 10
но убывает, т.е. ток отрицателен, то энергия, ранее накопленная в электрическом поле емкости, возвращается во внешнюю цепь. Энергия электрического поля в произвольный момент времени t (при условии, что при t=0 емкость не была заряжена) определится Рис.1.4. u c C .. i Условное обозначение емкости и положительные направления тока и напряжения приведены на рис.1.4. Мощность, поступающая в емкость, равна Когда заряд положителен и возрас-тает, то ток положителен, и в емкость поступает электрическая энергия извне. Когда заряд положителен, (1.22)
Слайд 11
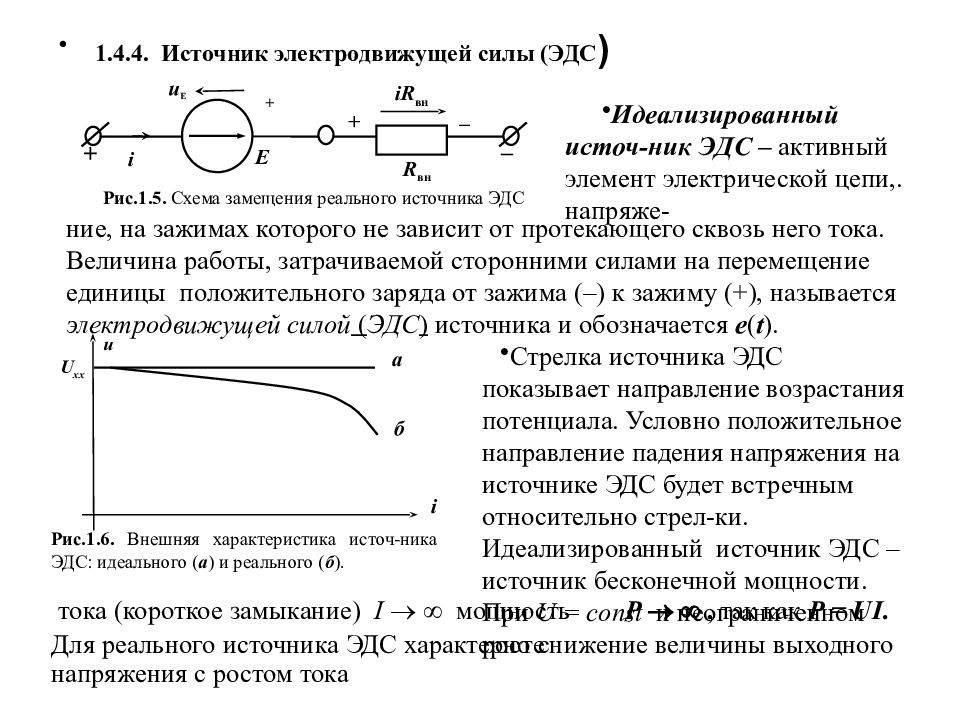
1.4.4. Источник электродвижущей силы (ЭДС ) Стрелка источника ЭДС показывает направление возрастания потенциала. Условно положительное направление падения напряжения на источнике ЭДС будет встречным относительно стрел-ки. Идеализированный источник ЭДС – источник бесконечной мощности. При U = const и неограниченном росте Идеализированный источ-ник ЭДС – активный элемент электрической цепи,. напряже- u Е – + Рис.1.5. Схема замещения реального источника ЭДС i iR вн R вн E + + – ние, на зажимах которого не зависит от протекающего сквозь него тока. Величина работы, затрачиваемой сторонними силами на перемещение единицы положительного заряда от зажима (–) к зажиму (+), называется электродвижущей силой ( ЭДС ) источника и обозначается e ( t ). u U хх Рис.1.6. Внешняя характеристика источ-ника ЭДС: идеального ( а ) и реального ( б ). i a б тока (короткое замыкание) I мощность Р , так как Р = UI. Для реального источника ЭДС характерно снижение величины выходного напряжения с ростом тока
Слайд 12
1.4.5. Источник тока Идеализированный источник тока – актив-ный элемент электрической цепи, ток которого не зависит от напряжения на его зажимах. Стрелка источника тока показывает направление протекания тока. Положительное направление падения напряжения на источнике тока будет встречным относительно стрелки (рис.1.7). Идеализированный источник тока – источник бесконечной мощности (рис.1.9 кривая а ). Для реального источника ЭДС характерно сниже-ние величины тока с ростом сопротивления во внешней цепи (рис.1.6 кривая 2 б ). Это сниже-ние объясняется наличием у источника внут-ренней проводимости G вн. Различают источ-ники постоянного тока и источники, ток которых есть функция времени. i I хх Рис.1.9. Внешняя характер-истика источника тока: идее-ального ( а ) и реального ( б ). e a б Рис.1.7. Идеальный источник тока i + J + – u i Рис.1.8. Схема замещения реального источника тока i G вн J u i вн
Слайд 13
Электрическая цепь и электрическая схема Электрической цепью называют совокупность устройств и объектов, образующих пути для протекания электрического тока. Элемент электрической цепи – отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определенную функцию. Активные элементы электрических цепей – источники электрической энергии, преобразующие в электрическую энергию другие виды энергии (механическую, химическую и др.). Пассивные элементы электрических цепей – элементы электрической цепи, преобразующие электрическую энергию в другие виды энергии. Все элементы электрических цепей разделяют на две группы: линейные и нелинейные.
Слайд 14
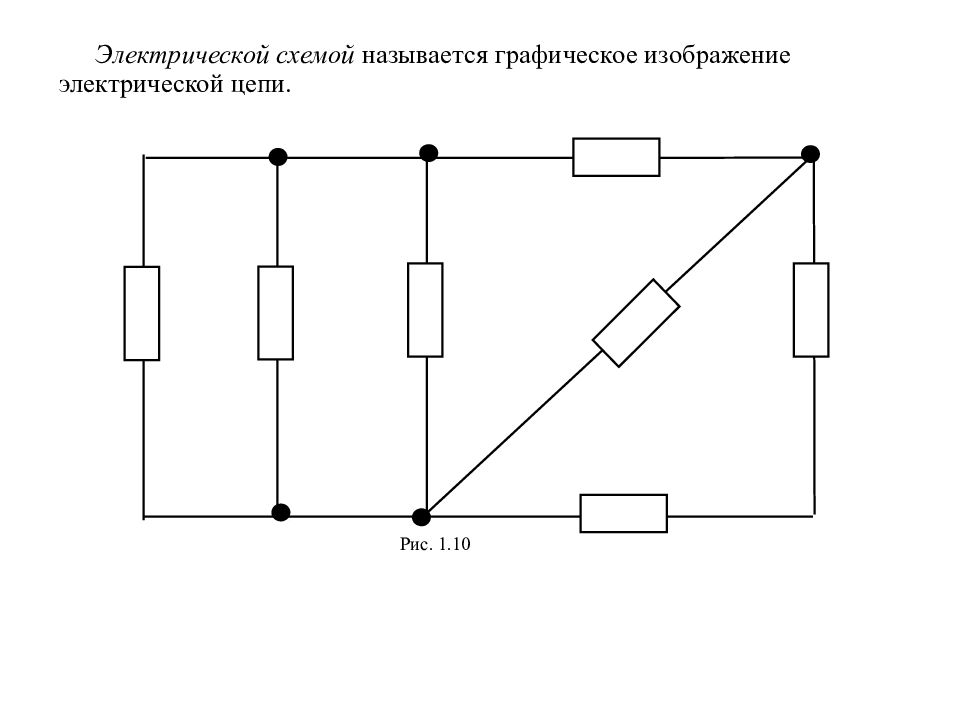
Электрической схемой называется графическое изображение электрической цепи. Рис. 1.10
Слайд 15
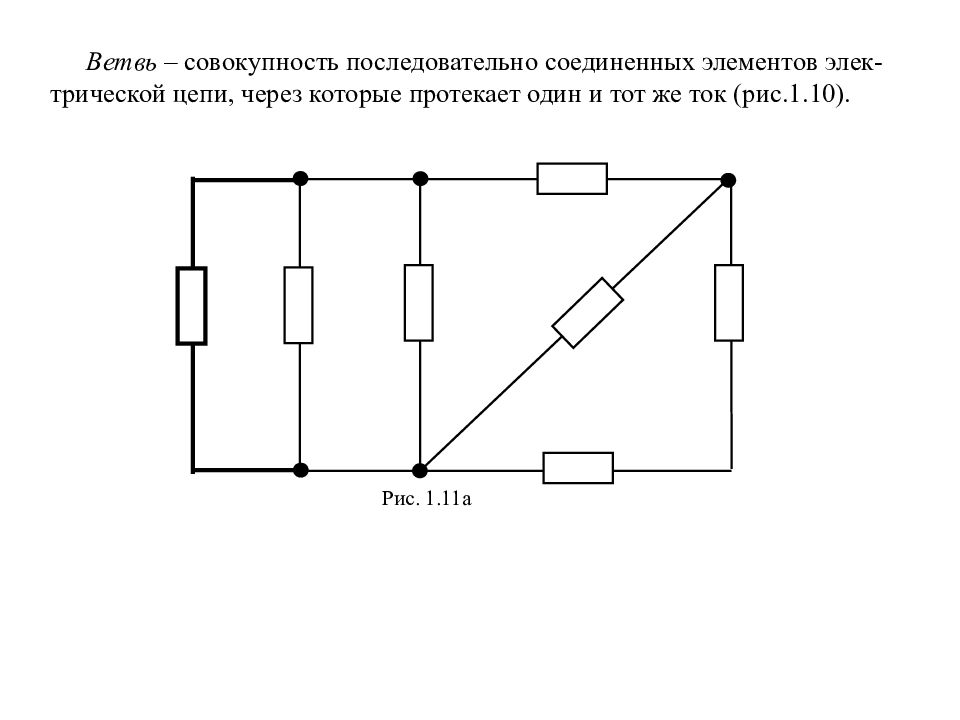
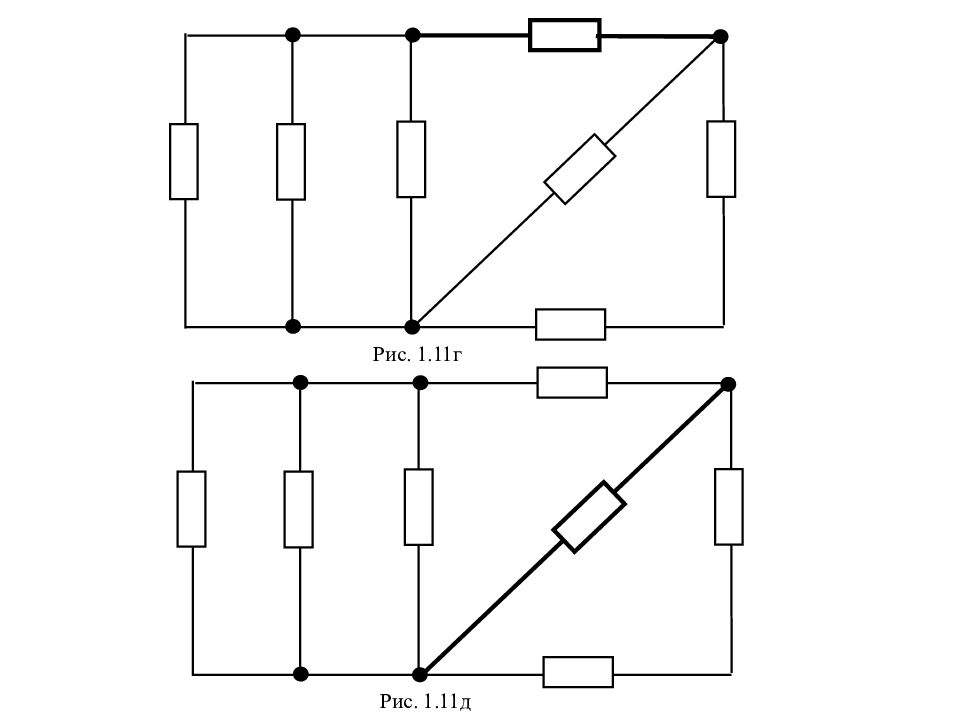
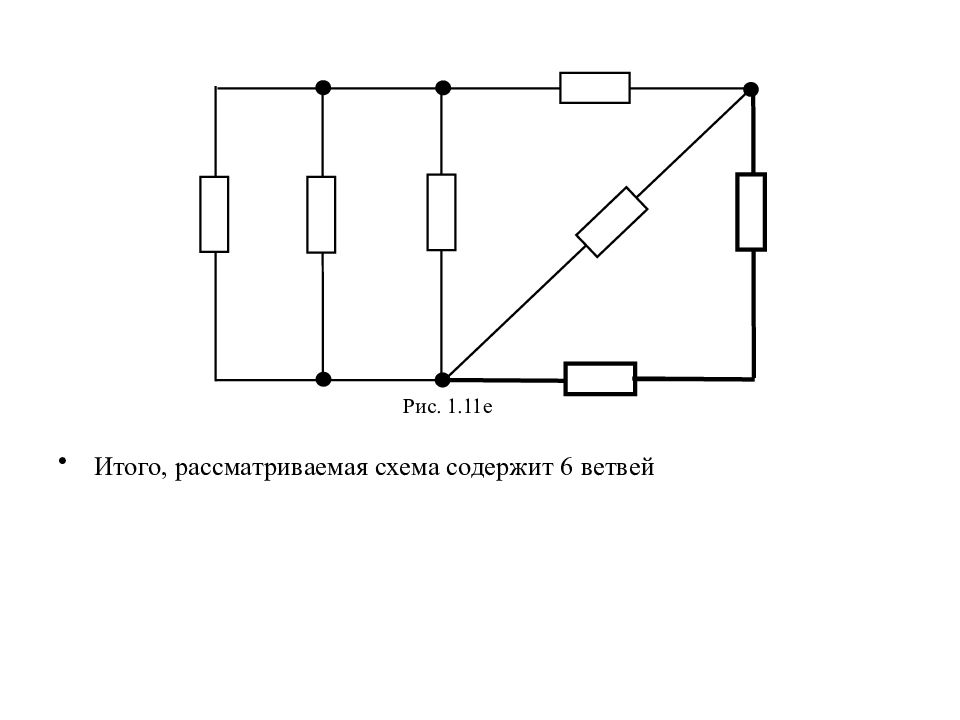
Ветвь – совокупность последовательно соединенных элементов элек-трической цепи, через которые протекает один и тот же ток (рис.1.10). Рис. 1.11а
Слайд 19
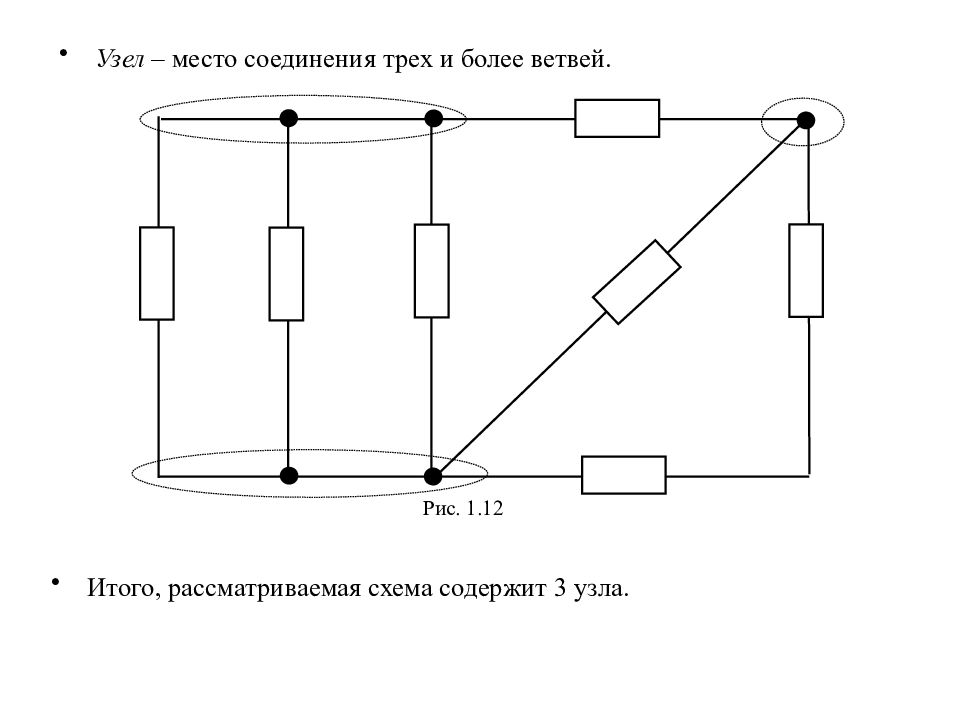
Узел – место соединения трех и более ветвей. Рис. 1.12 Итого, рассматриваемая схема содержит 3 узла.
Слайд 20
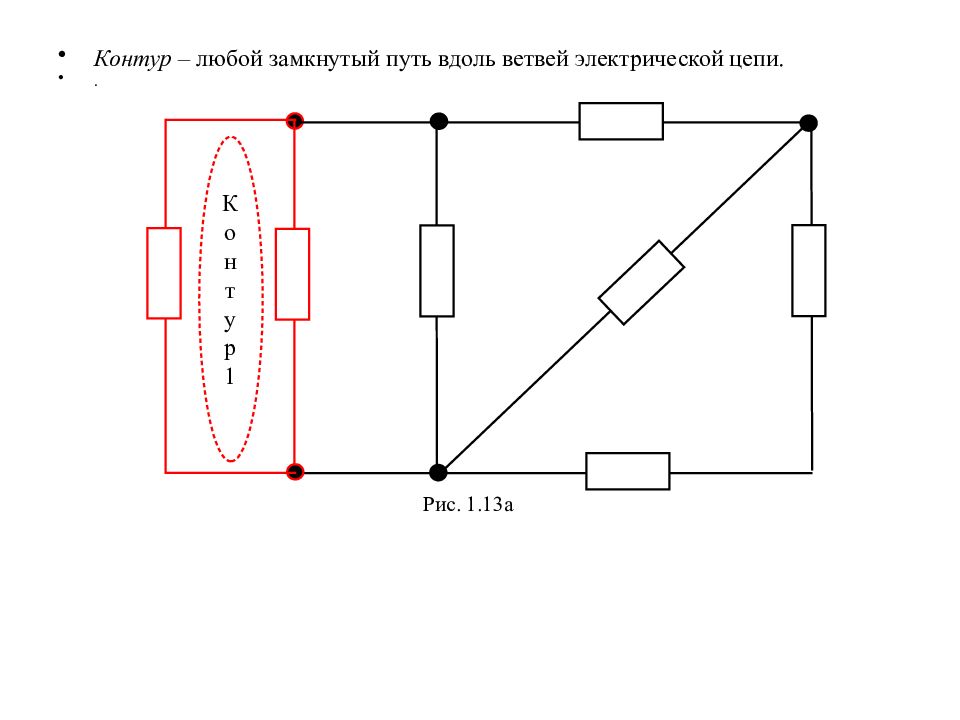
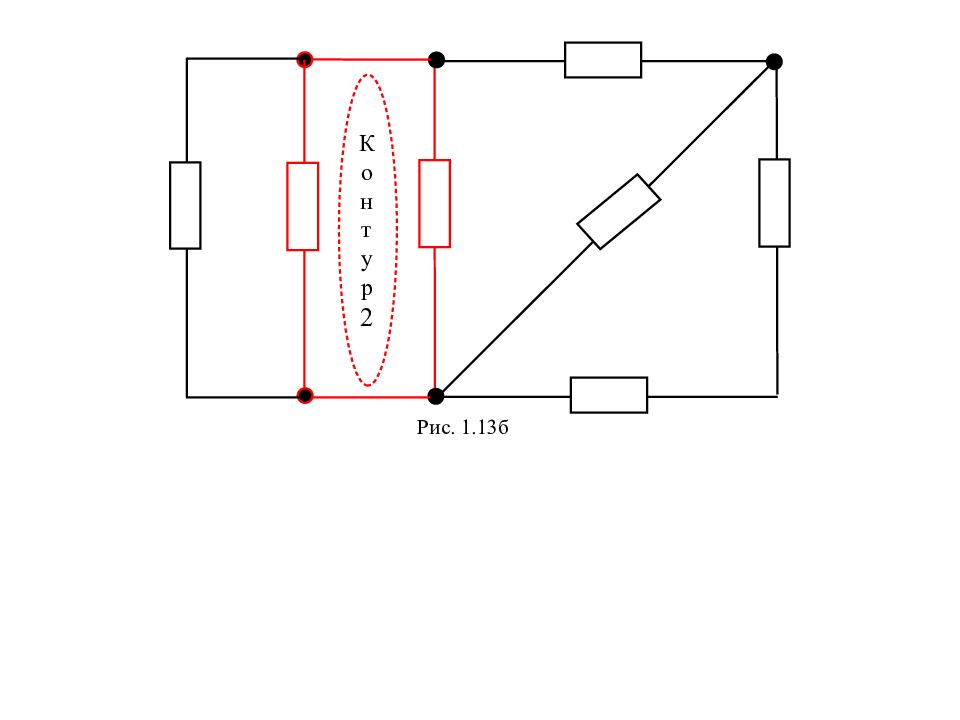
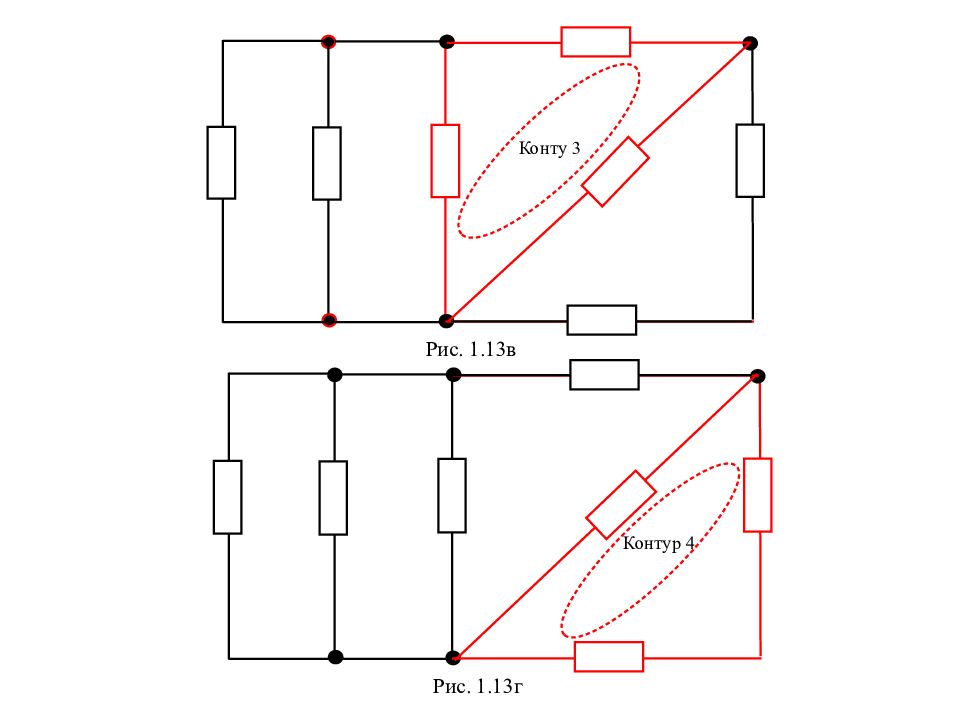
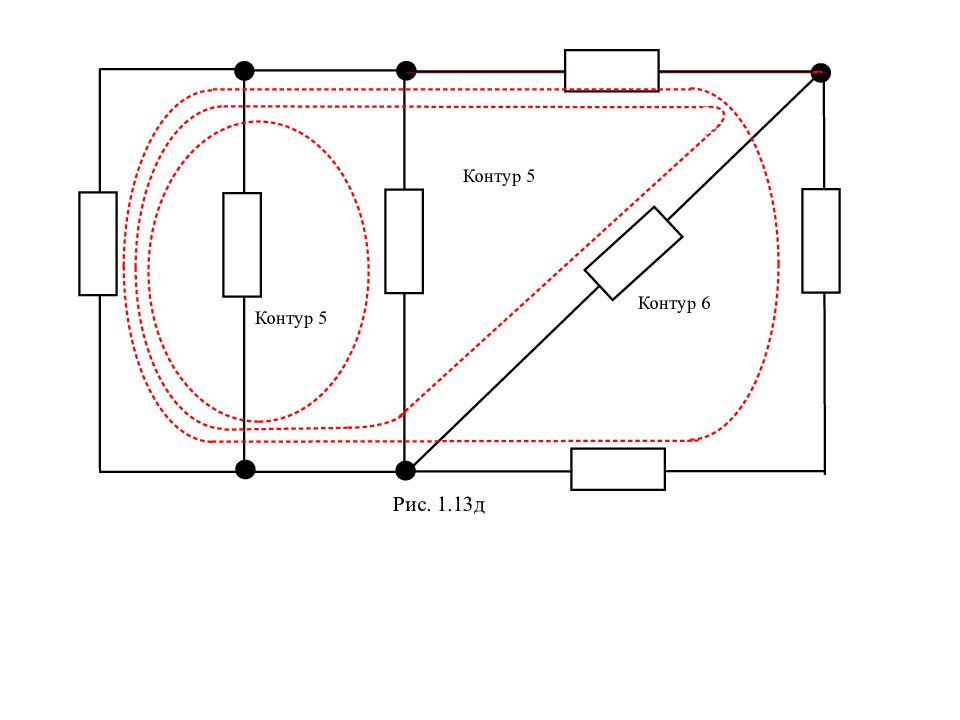
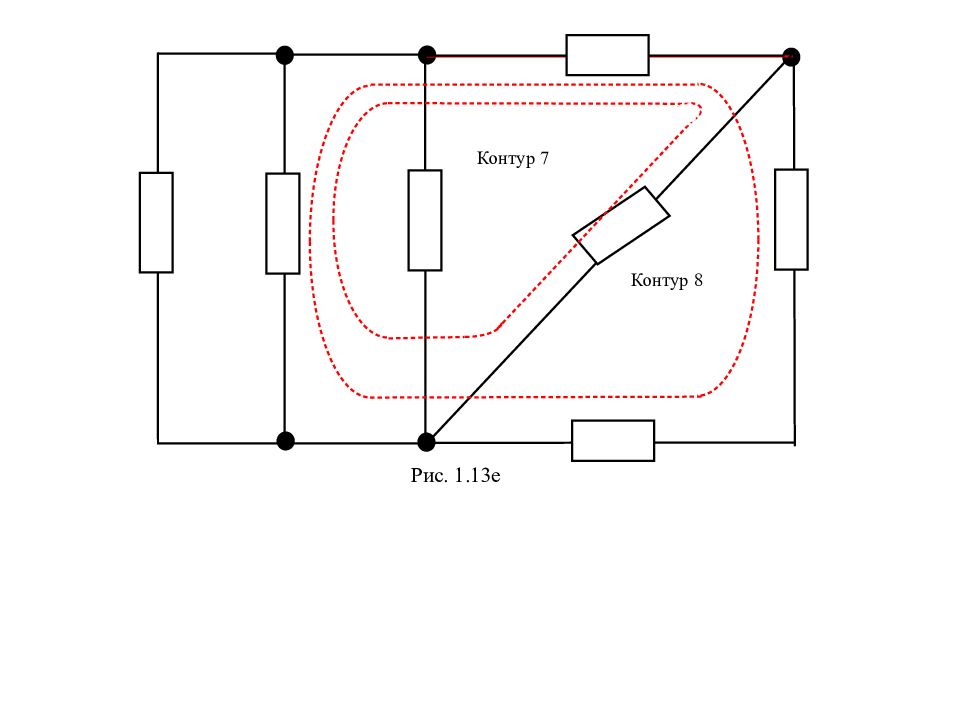
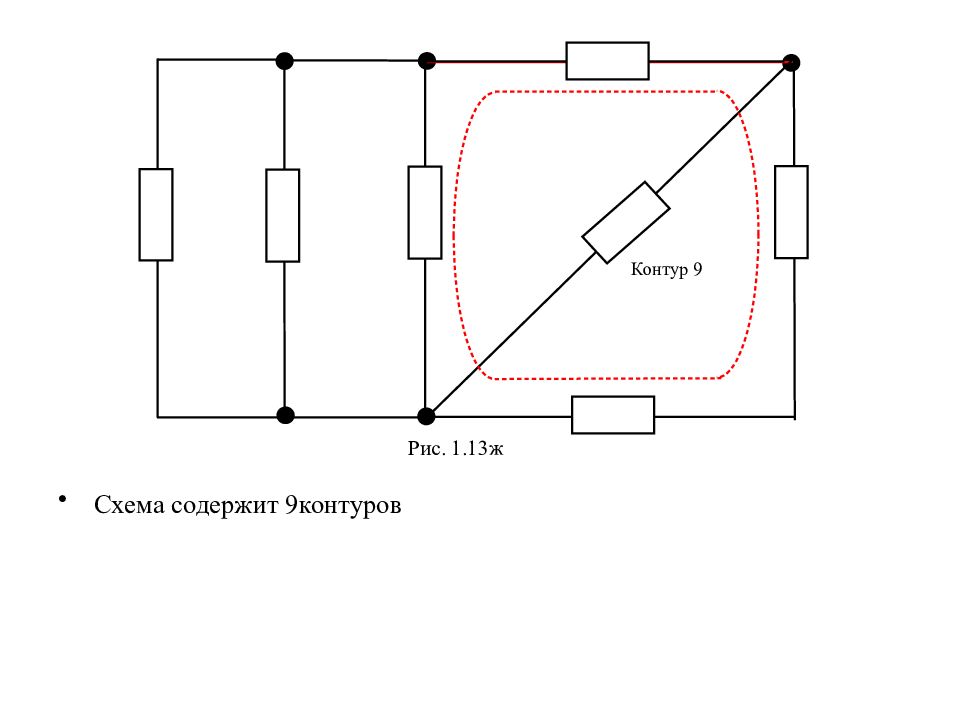
Контур – любой замкнутый путь вдоль ветвей электрической цепи. . Рис. 1.13а К о н т у р 1
Слайд 26
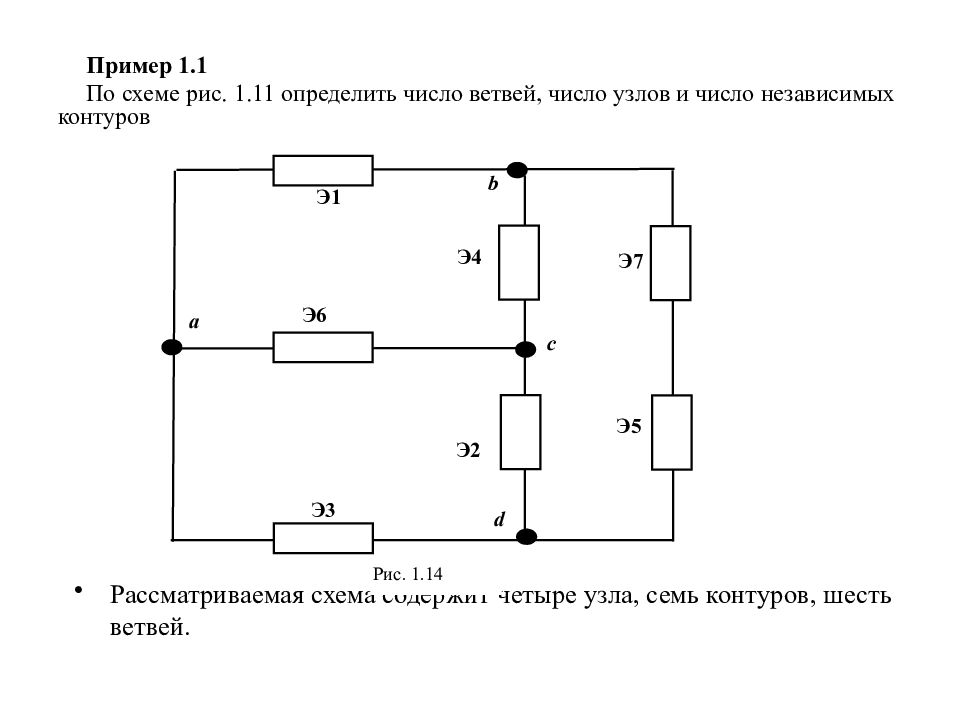
Пример 1.1 По схеме рис. 1.11 определить число ветвей, число узлов и число независимых контуров Рассматриваемая схема содержит четыре узла, семь контуров, шесть ветвей. d c b a Э 6 Э 1 Э 3 Э 4 Э 7 Э 2 Э 5 Рис. 1.14
Слайд 27
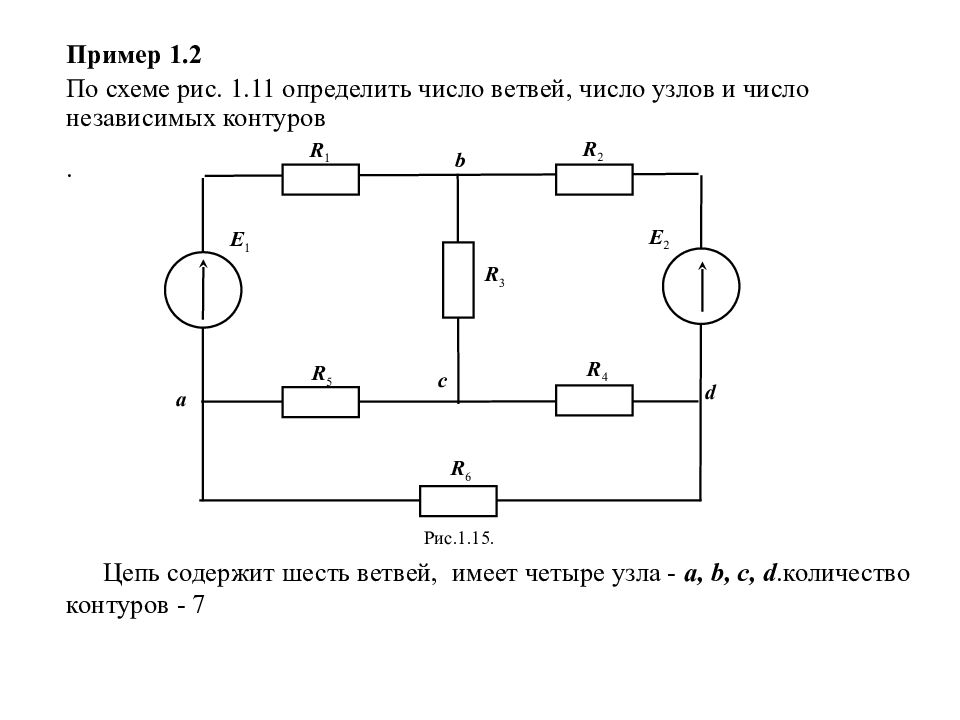
Цепь содержит шесть ветвей, имеет четыре узла - a, b, c, d.количество контуров - 7 Рис.1.1 5. a c b d E 1 E 2 R 1 R 2 R 3 R 4 R 5 R 6 Пример 1.2 По схеме рис. 1.11 определить число ветвей, число узлов и число независимых контуров .
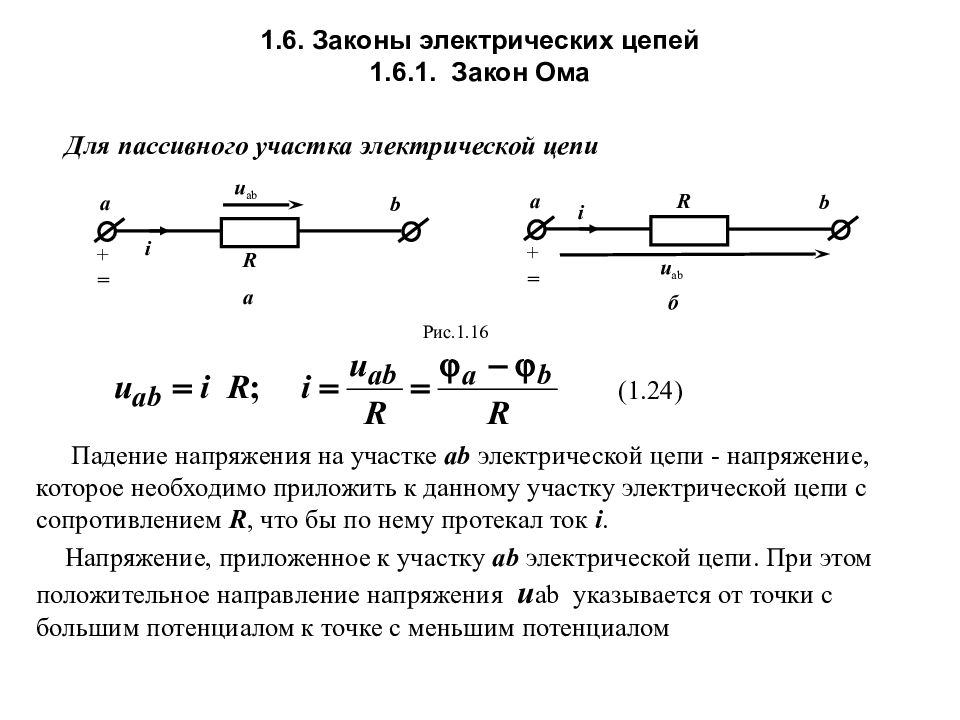
Для пассивного участка электрической цепи Падение напряжения на участке а b электрической цепи - напряжение, которое необходимо приложить к данному участку электрической цепи с сопротивлением R, что бы по нему протекал ток i. Напряжение, приложенное к участку а b электрической цепи. При этом положительное направление напряжения u ab указывается от точки с большим потенциалом к точке с меньшим потенциалом Рис.1.1 6 R u ab a + = i b a R u ab a + = i b б (1.24)
Слайд 29
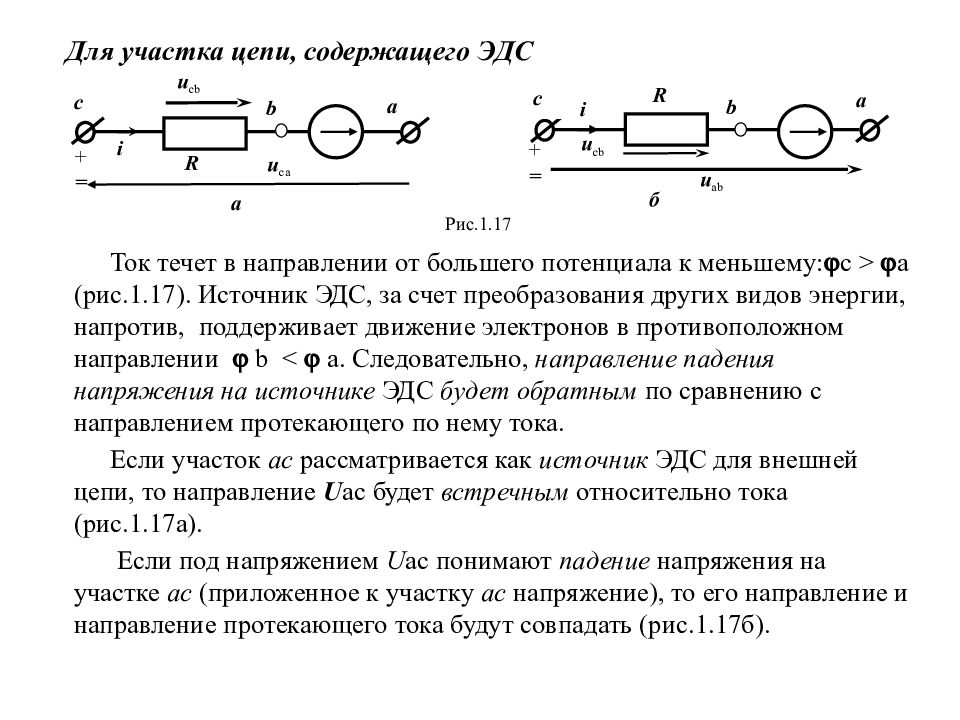
Для участка цепи, содержащего ЭДС Ток течет в направлении от большего потенциала к меньшему: c > a (рис.1.17). Источник ЭДС, за счет преобразования других видов энергии, напротив, поддерживает движение электронов в противоположном направлении b < а. Следовательно, направление падения напряжения на источнике ЭДС будет обратным по сравнению с направлением протекающего по нему тока. Если участок ас рассматривается как источник ЭДС для внешней цепи, то направление U a с будет встречным относительно тока (рис.1.17а). Если под напряжением U a с понимают падение напряжения на участке ас (приложенное к участку ас напряжение), то его направление и направление протекающего тока будут совпадать (рис.1.17б). u cb u ca с Рис.1.1 7 R u cb a + = i b a R u ab a + = i c б b
Слайд 30
При определения тока участка цепи можно воспользоваться неслож-ным правилом: в числителе – все что способствует нарастанию тока (ЭДС, напряжение на концах участка – совпадение их направлений с направлением тока) берут со знаком ‘+’, все что препятствует (встреч-ные направления) – со знаком ‘–’; в знаменателе – суммарное сопротивление ветви: (1.25) для рис.1.17а для рис.1.17б В общем случае для любого участка цепи (1.26)
Слайд 31
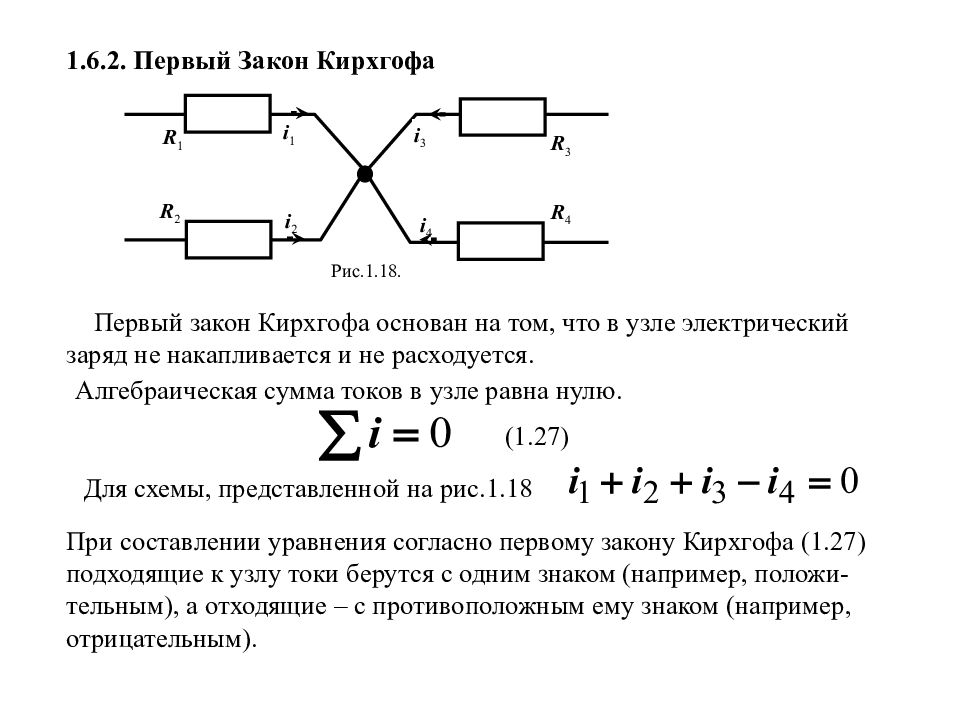
1.6.2. Первый Закон Кирхгофа i 2 i 4 R 1 R 2 R 3 R 4 i 1 Рис.1.18. i 3 Первый закон Кирхгофа основан на том, что в узле электрический заряд не накапливается и не расходуется. Алгебраическая сумма токов в узле равна нулю. (1.27) Для схемы, представленной на рис.1.18 При составлении уравнения согласно первому закону Кирхгофа (1.27) подходящие к узлу токи берутся с одним знаком (например, положи-тельным), а отходящие – с противоположным ему знаком (например, отрицательным).
Слайд 32
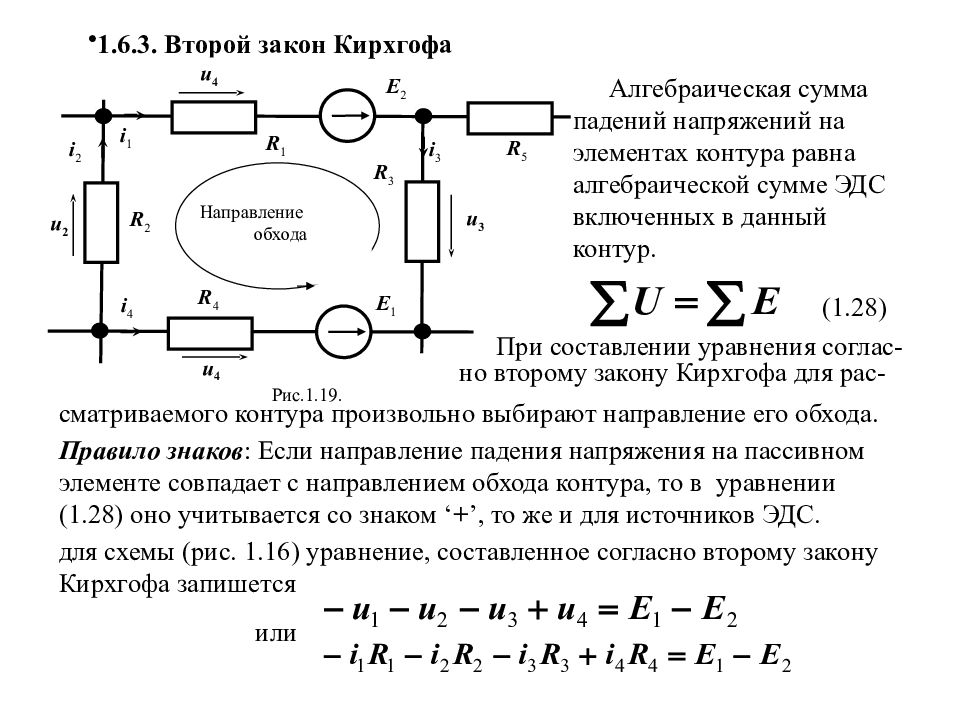
1.6.3. Второй закон Кирхгофа сматриваемого контура произвольно выбирают направление его обхода. Правило знаков : Если направление падения напряжения на пассивном элементе совпадает с направлением обхода контура, то в уравнении (1.28) оно учитывается со знаком ‘ + ’, то же и для источников ЭДС. для схемы (рис. 1.16) уравнение, составленное согласно второму закону Кирхгофа запишется Алгебраическая сумма падений напряжений на элементах контура равна алгебраической сумме ЭДС включенных в данный контур. (1.28) E 1 E 2 u 4 u 2 i 2 i 1 i 4 R 1 R 2 R 3 R 4 i 3 Рис.1.19. u 4 Направление обхода R 5 u 3 При составлении уравнения соглас-но второму закону Кирхгофа для рас- или
2.1. Синусоидальные ЭДС, напряжения и токи Рассмотрим основные способы представления синусоидальных величин – частота – физическая величина, определяющая число коле баний в единицу времени (Гц); Т – период– время одного полного колебания (с) i, u, е– начальные фазовые углы e, u, i – мгновенные значения ЭДС, напряжения и тока; I m, U m, E m – амплитудные значения соответствующих величин; – круговая (цикличес-кая) частота;
Слайд 35
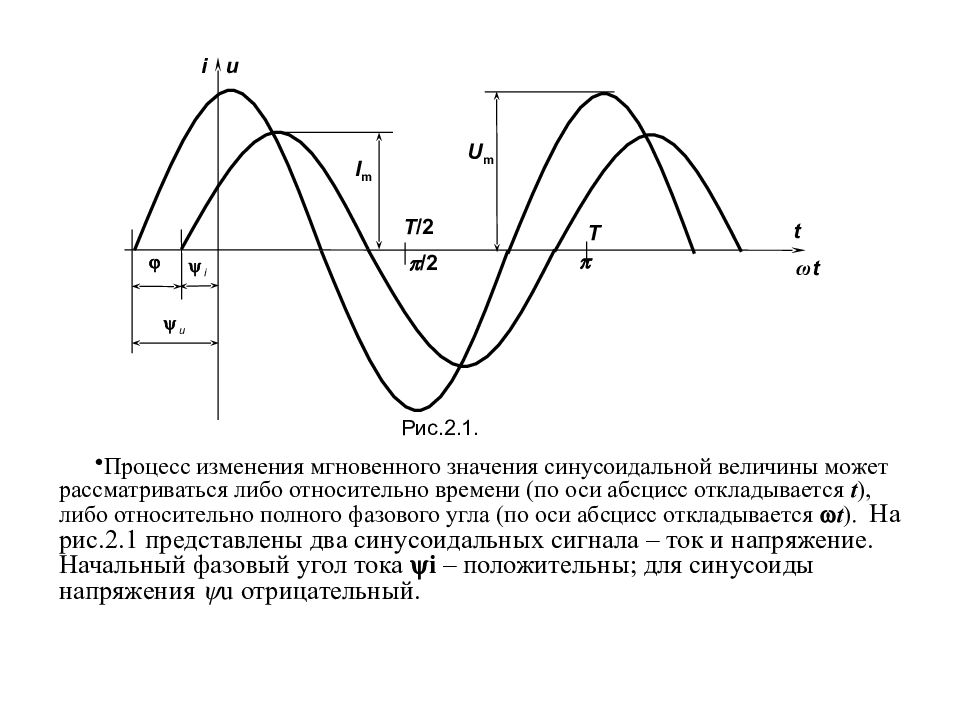
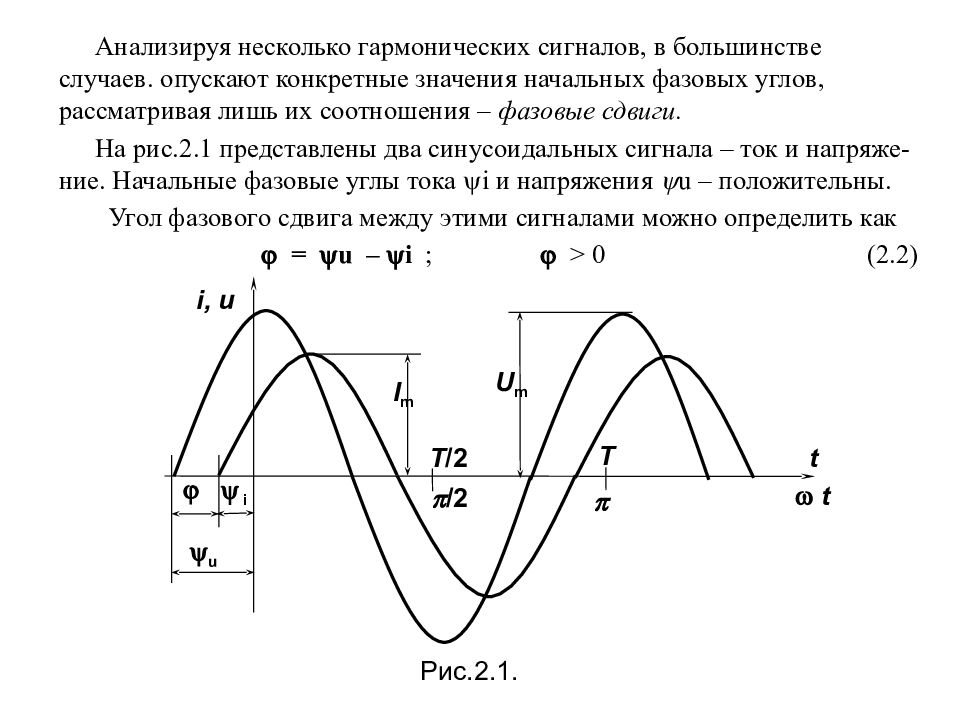
Процесс изменения мгновенного значения синусоидальной величины может рассматриваться либо относительно времени (по оси абсцисс откладывается t ), либо относительно полного фазового угла (по оси абсцисс откладывается t ). На рис.2.1 представлены два синусоидальных сигнала – ток и напряжение. Начальный фазовый угол тока i – положительны; для синусоиды напряжения u отрицательный. U m I m i /2 i u Рис.2.1. Т /2 Т ω t t u
Слайд 36
2.2. Представление синусоидальной величины комплексными числами. 2.2.1. Определение комплексного числа Комплексным числом называется упорядоченная пара действительных чисел а и b где a = Re ( Z ) – действительная часть комплексного числа Z, b = Im ( Z ) – мнимая часть комплексного числа Z, j – мнимая единица ( j 2 = –1). действительная часть комплексного числа Re ( Z 1 ) = 4; мнимая часть комплексного числа Im ( Z 1 ) = 3. действительная часть комплексного числа Re ( Z 1 ) = -3; мнимая часть комплексного числа Im ( Z 1 ) = 5. действительная часть комплексного числа Re ( Z 1 ) = 0; мнимая часть комплексного числа Im ( Z 1 ) = -2. действительная часть комплексного числа Re ( Z 1 ) = 4; мнимая часть комплексного числа Im ( Z 1 ) = 0.
Слайд 37
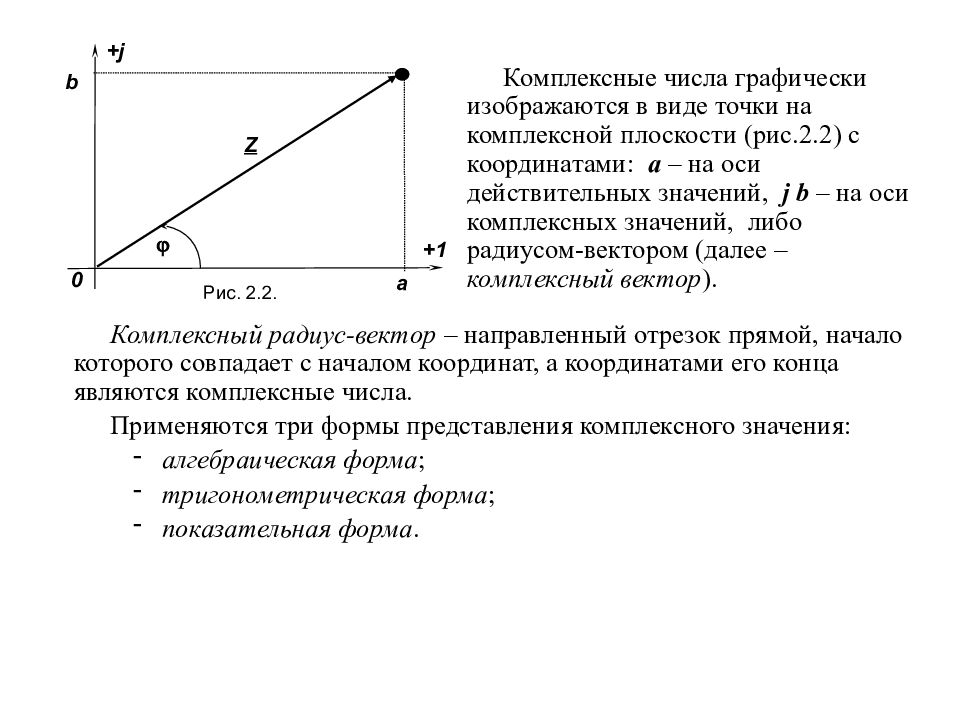
Комплексные числа графически изображаются в виде точки на комплексной плоскости (рис.2.2) с координатами: a – на оси действительных значений, j b – на оси комплексных значений, либо радиусом-вектором (далее – комплексный вектор ). Рис. 2.2. Z +j +1 a 0 b Комплексный радиус-вектор – направленный отрезок прямой, начало которого совпадает с началом координат, а координатами его конца являются комплексные числа. Применяются три формы представления комплексного значения: алгебраическая форма ; тригонометрическая форма ; показательная форма.
Слайд 38
2.2.2. Алгебраическая форма представления комплексного числа Комплексное число представленное в алгебраической форме имеет вид , (2.3) Длина или модуль комплексного вектора определяется по его проекциям на оси исходя из прямоугольного треугольника (рис.2.2) . (2.4) Аргументом комплексного числа называется угол между действительной осью и комплексным вектором. Если > 0, то угол отсчитывается в направлении против движения часовой стрелки, если < 0, – наоборот. Аргумент связан с действительной и мнимой частями комплексного числа соотношением (2.5)
Слайд 39
Если два комплексных числа отличаются только знаком перед мнимой частью, то такие комплексные числа называются сопряженными. Для любого комплексного числа существует сопряженное комплексное число, обозначаемое Для каждого из заданных комплексных чисел найти модуль, аргумент и сопряженное комплексное число. сопряженное комплексное число модуль комплексного числа аргумент комплексного числа модуль комплексного числа аргумент комплексного числа сопряженное комплексное число
Слайд 40
модуль комплексного числа аргумент комплексного числа сопряженное комплексное число модуль комплексного числа аргумент комплексного числа сопряженное комплексное число отсутствует так как рассматриваемое число действительное
Слайд 41
2.2.3. Тригонометрическая форма представления комплексного числа Проекции комплексного вектора на действительную и мнимую оси определяются (2.6) Подставив эти значения в (2.3), получим тригонометрическую форму записи комплексного числа (2.7) 2.2.4. Показательная форма представления комплексного числа Показательная форма удобна для выполнения операций умножения и деления над комплексными числами. Используя формулу Эйлера можно комплексного числа, записанные в тригонометрической форме, ,представить в показательной форме (2.8)
Слайд 42
Пример 2.3 Задано комплексное число . Представить данное число в тригонометрической и показательной формах и. изобразить его на комплексной плоскости. Рис. 2.3. + j Z 10 + 0 Решение – алгебраическая форма. Проекция на ось действительных значений равна, на ось мнимых значений – 10 (рис.2.3). Модуль комплекс-ного числа – Z M определяется формулой (2.4) Аргумент комплексного числа определяется формулой (2.5) Тригонометрическая форм согласно формуле (2.7) Показательная форма
Слайд 43
Задано комплексное число – алгебраическая форма. Проекция на ось действительных значений равна, на ось мнимых значений равна –10 (рис.2.4). Рис. 2.4. + j Z 10 + 0 Пример 2.4 Аргумент комплексного числа определяется формулой (2.5) Тригонометрическая форм согласно формуле (2.7) Показательная форма Модуль Z M определяется как (рис.2.5)
Слайд 44
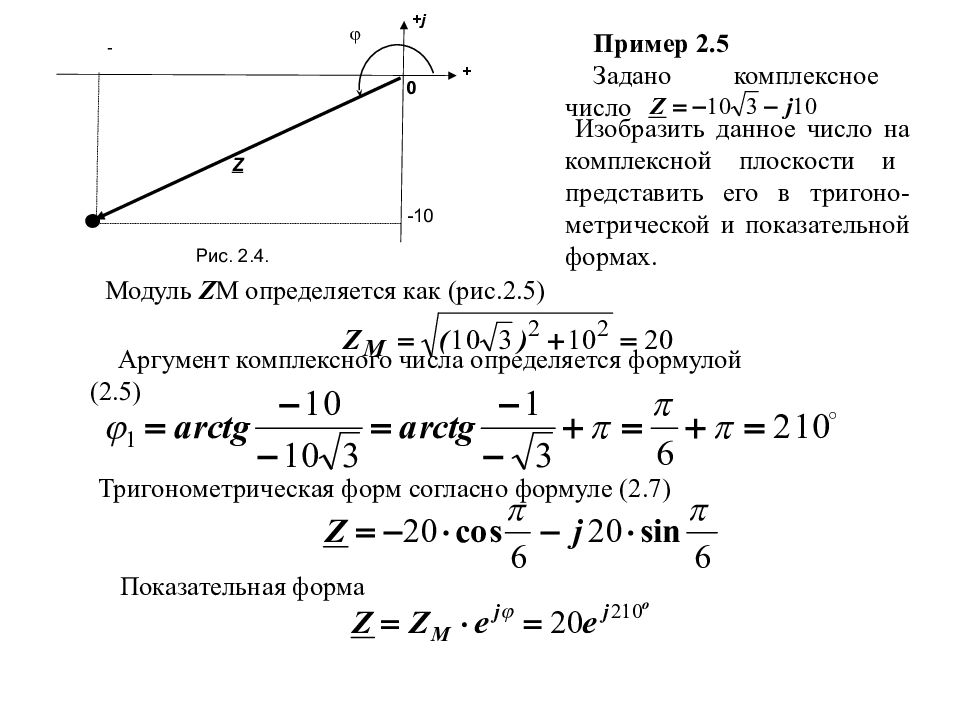
Пример 2.5 Задано комплексное число Изобразить данное число на комплексной плоскости и представить его в тригоно - метрической и показательной формах. Рис. 2.4. + j Z -10 + 0 - Аргумент комплексного числа определяется формулой (2.5) Тригонометрическая форм согласно формуле (2.7) Показательная форма Модуль Z M определяется как (рис.2.5)
Слайд 45
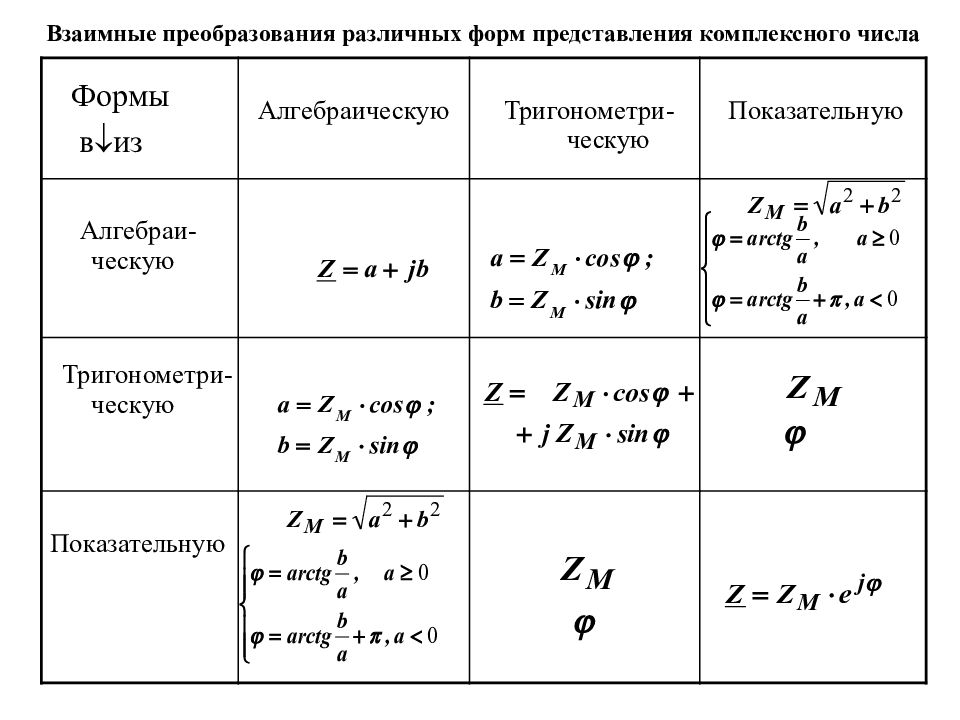
Формы в из Алгебраическую Тригонометри-ческую Показательную Алгебраи-ческую Тригонометри-ческую Показательную Взаимные преобразования различных форм представления комплексного числа
Слайд 46
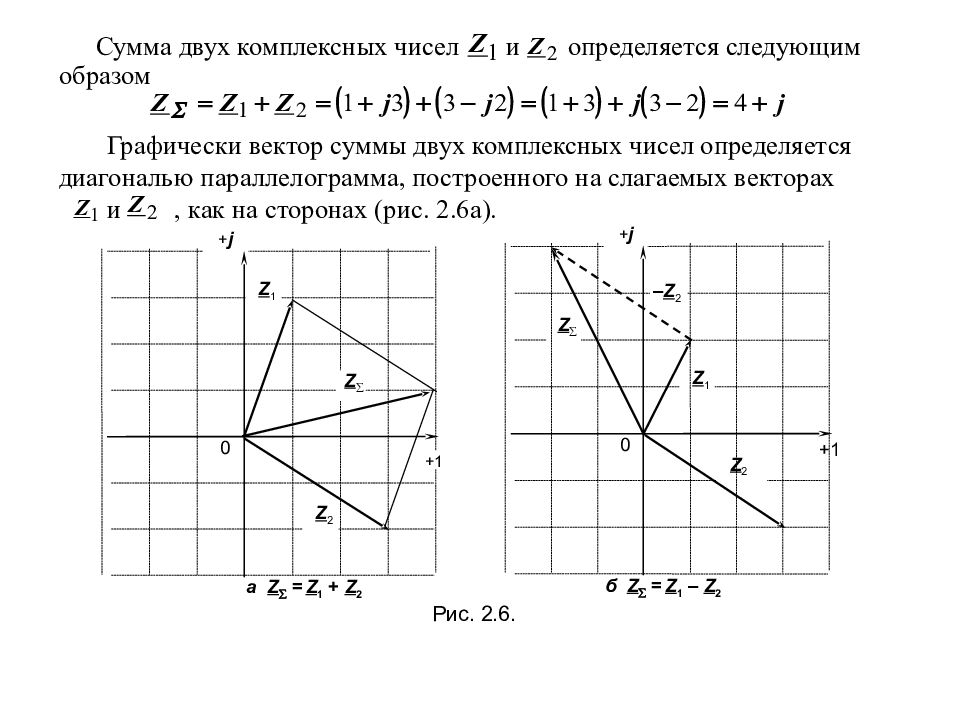
Пример 2.6 Произвести сложение и вычитание и построить вектор, соответствующий сумме (разности) следующих комплексных чисел: и Решение Сумма двух комплексных чисел и определяется следующим образом Графически вектор суммы двух комплексных чисел и опре-деляется диагональю параллелограмма, построенного на слагаемых векторах, как на сторонах (рис. 2.6а).
Слайд 47
2.2.5. Основные математические операции над комплексными числами Сложение (Вычитание) Заданы два комплексных числа и Для сложения (вычитания) достаточно сложить (вычесть) соответственно действительные и мнимые их части. Для этой цели наиболее удобно п ред - ставлять комплексные числа в алгебраической форме Геометрический смысл этих операций сводится к сложению (вычитанию) векторов и, построенных на комплексной плоскости. Зададимся двумя комплексными числами : и Сумма : Сумма сопряженных комплексных чисел – действительное число. (2.9) Разность : Пример 2.6 Произвести сложение и вычитание и построить вектор, соответствующий сумме (разности) следующих комплексных чисел: и .
Слайд 48
Сумма двух комплексных чисел и определяется следующим образом Графически вектор суммы двух комплексных чисел определяется диагональю параллелограмма, построенного на слагаемых векторах и, как на сторонах (рис. 2.6а). 0 + j + 1 Z 1 Z 2 Z a Z = Z 1 + Z 2 Рис. 2.6. б Z = Z 1 – Z 2 0 + j + 1 Z 1 Z – Z 2 Z 2
Слайд 49
Разность двух комплексных чисел и определяется как Графически вектор разности двух комплексных чисел определяется диагональю параллелограмма, построенного на векторах и, как на сторонах (рис. 2.6 б ). Умножение (Деление) Для умножения (деления) комплексных чисел наиболее удобно представлять их в показательной форме. Чтобы перемножить (разделить) два комплексных числа нужно перемножить (разделить) их модули и сложить (вычесть) аргументы. Заданы два комплексных числа и Произведение этих чисел определится формулой Если комплексные числа заданы в алгебраической форме и , то для выполнения операции умножения возможен либо переход к показательной форме, либо как умножение двух многочленов с учетом, что (2.10)
Слайд 50
Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа (2.11) (2.12) Частное от деления на, если они заданы в показательной форме, определится формулой (2.13) Если комплексные числитель и знаменатель заданы в алгебраической форме, то для выполнения операции деления возможен либо переход к показательной форме, либо формирование в знаменателе действительного числа (домножение и знаменателя, и числителя на сопряженное знамена-телю комплексное число). (2.14)
Слайд 51
Пример 2.7 Найти произведение и частное двух комплексных чисел: и 1. Произведение и частное двух комплексных чисел и проведем согласно формулам (2.11) и (2.14) , . и 2. Представим комплексные числа и в показательной форме, используя формулы (2.4) и (2.5) для определения модуля и аргумента. Действительная часть комплексного числа равна 0, а мнимая -( 2). Находим модуль и аргумент Зная модуль и аргумент, запишем
Слайд 52
Находим модуль и аргумент Действительная часть комплексного числа равна а мнимая Зная модуль и аргумент, запишем Произведение и определим согласно формуле (2.10) Частноеот деления и определим согласно формуле (2.11)
Слайд 53
2.1. Синусоидальные ЭДС, напряжения и токи В качестве основного электрического сигнала промыш - ленных и бытовых электросетей выбрана синусоидально изменяющаяся величина: ток, напряжение, ЭДС. Такой выбор обоснован тем, что получение и преобразование переменного тока значительно проще и дешевле, нежели постоянного. Рассмотрим основные способы представления синусоидальных величин. ; ;, (2.1) где: e, u, i – мгновенные значения ЭДС, напряжения и тока; I m, U m, E m – их амплитудные значения; ω – круговая (циклическая) частота; f – частота –величина, определяющая число колебаний в секунду (Гц); Т – период – время одного полного колебания (с); i, u, е – начальные фазовые углы
Слайд 54
Анализируя несколько гармонических сигналов, в большинстве случаев. опускают конкретные значения начальных фазовых углов, рассматривая лишь их соотношения – фазовые сдвиги. На рис.2.1 представлены два синусоидальных сигнала – ток и напряже-ние. Начальные фазовые углы тока i и напряжения u – положительны. Угол фазового сдвига между этими сигналами можно определить как = u – i ; > 0 (2.2) U m I m t i u /2 Т Т /2 t i, u Рис.2.1.
Слайд 55
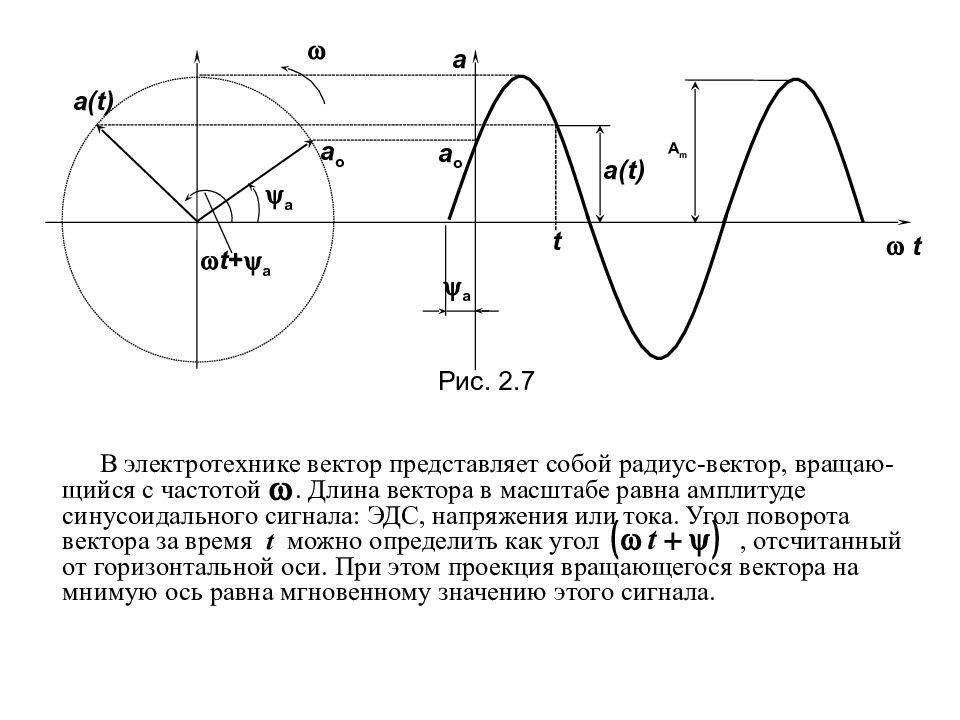
2.3. Представление синусоидальных функций вращающимися векторами Любая синусоидальная величина в электротехнике может быть представлена вращающимся на комплексной плоскости вектором. Рассмотрим синусоидальный сигнал а a = A m sin ( t + a), (2.15) который может быть любым исследуемым электрическим сигналом ( Е, U, I ). Нетрудно заметить, что мгновенное значение синусоидаль-ной функции а, есть не что иное, как проекция вектора, вращающегося в комплексной плоскости со скоростью , на ось мнимых значений. Наглядно представление синусоидального сигнала вращающимся вектором показано на рис. 2.7.
Слайд 56
В электротехнике вектор представляет собой радиус-вектор, вращаю- щийся с частотой. Длина вектора в масштабе равна амплитуде синусоидального сигнала: ЭДС, напряжения или тока. Угол поворота вектора за время t можно определить как угол, отсчитанный от горизонтальной оси. При этом проекция вращающегося вектора на мнимую ось равна мгновенному значению этого сигнала. a(t) a(t) a o Рис. 2.7 а а а t t + а a o t A m
Слайд 57
Пример 2.8 Заданы два электрических сигнала где E 1m и E 2m – амплитуды; – круговая частота переменного тока; 1, 2 – начальные фазовые углы ЭДС. Определить сумму этих ЭДС. Решение Сложим сигналы e 1 и e 2 как две тригонометрические функции Обозначим постоянные выражения в скобках В итоге получим
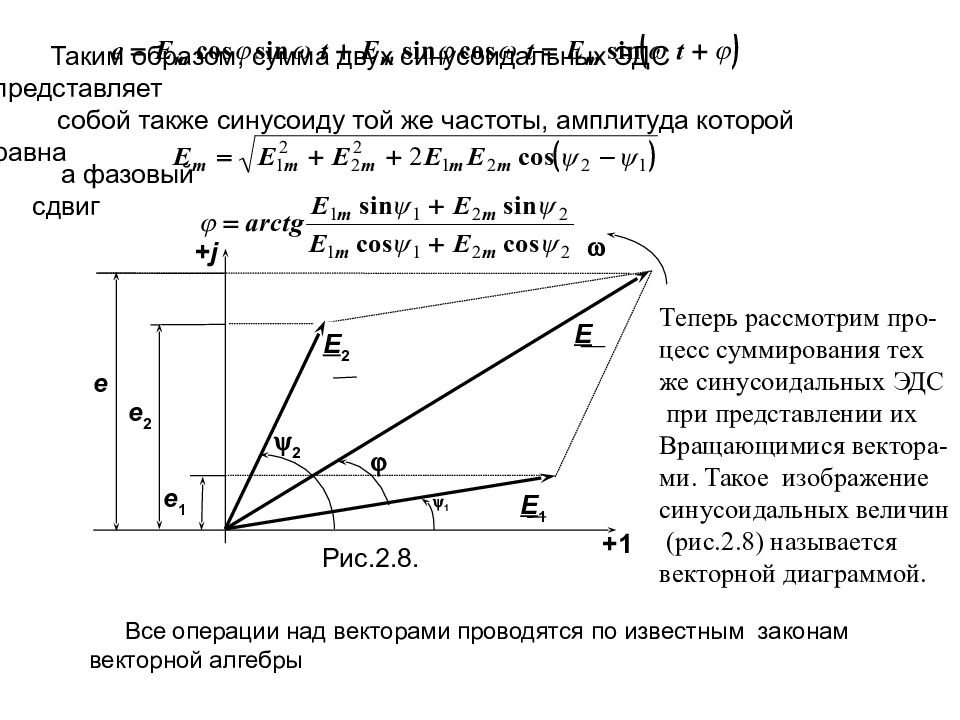
Слайд 58
e e 2 e 1 2 1 +j +1 Рис.2.8. Е Е 2 Е 1 Таким образом, сумма двух синусоидальных ЭДС представляет собой также синусоиду той же частоты, амплитуда которой равна а фазовый сдвиг Теперь рассмотрим про- цесс суммирования тех же синусоидальных ЭДС при представлении их Вращающимися вектора- ми. Такое изображение синусоидальных величин (рис.2.8) называется векторной диаграммой. Все операции над векторами проводятся по известным законам векторной алгебры
Слайд 59
2.4. Векторные диаграммы В установившихся режимах, то есть режимах, при которых амплитуды и частота синусоидальных сигналов остаются неизменными, соотношения мгновенных значений токов и напряжений также остаются неизменными. Следовательно, неизменным останется и расположение соответствующих комплексных векторов. Поэтому, векторные диаграммы, в большинстве случаев, строятся относи - тельно нулевого момента времени (составляющая t равна нулю), то есть с учетом только лишь начальных фазовых углов соответствующих электрических сигналов.. Рассмотрим вектор, изображающий ток в цепи: Мнимая часть этого вектора характеризует мгновен- ное значение тока Мнимая часть этого вектора характери- зует мгновенное значение тока Напряжение U изображается вектором
Слайд 60
Для момента времени t = 0, , где - комплексная амплитуда тока (комплексная величина с модулем I m и начальным фазовым углом i ). Аналогично для вектора напряжения где -комплексная амплитуда напряжения (комплексная величина с модулем U m и начальным фазовым углом ( i + )), Мгновенное значение напряжения
Слайд 61
Пример 2.9 Задано мгновенное значение тока . Представить это значение в показательной форме комплексного числа. Решение Показательная форма комплексного числа: Из условия: амплитудное значение тока : начальный фазовый угол .Следовательно, показательная форма тока: Пример 2.10 Дан комплексный ток . Определить мгновенное значение тока и начальный фазовый угол. Решение Для перехода к мгновенному значению надо умножить на и взять коэффициент при мнимой части от полученного произведения
Слайд 62
2.5. Действующие значения ЭДС, напряжения и тока Действующее значение – среднеквадратичное значение изменяющейся во времени величины за период, например переменного тока, действие которого при протекании его через некоторое сопротивление идентично действию постоянного тока определенного значения. (2.16) Среднее за период T значение мощности, характеризуемое выделением тепла в цепи с сопротивлением r, имеет выражение (2.17) то есть получаем выражение для средней мощности переменного тока такое же, как для постоянного тока. Определим связь действующего значения E синусоидальной ЭДС с амплитудой E m. Имеем
Слайд 63
так как то (2.18) Аналогично ; ; (2.19) Большая часть электроизмерительных приборов определяют действующие значения энергетических величин. Пример 2.11 Найти комплекс действующего значения синусоидальной функции времени Решение Учитывая, что косинус функция четная, выражение перепишем в виде Амплитуда синусоидального тока начальная фаза Отсюда: А. А. А.
Слайд 64
Пример 2.11 Найти комплекс действующего значения синусоидальной функции времени Решение Учитывая, что косинус функция четная, выражение перепишем в виде Амплитуда синусоидального тока начальная фаза Отсюда: А. А. А.
Слайд 66
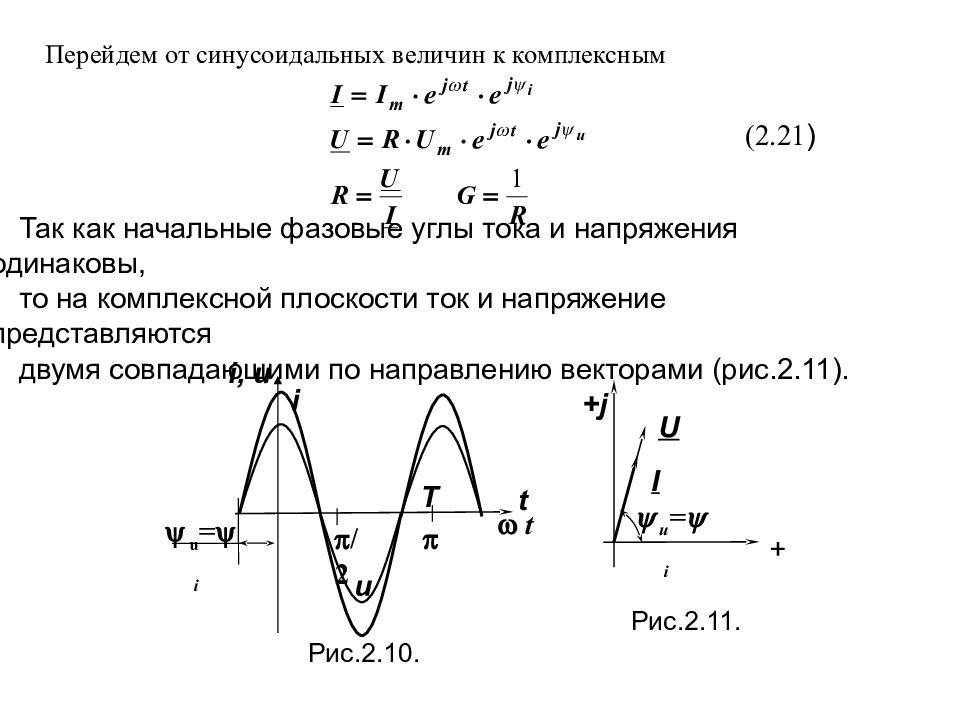
Рис.2.9. а b u ab R i 2.6. Элементы цепи синусоидального тока 2.6.1. Резистор в цепи синусоидального тока Пропустим через активное сопротивление R переменный электрический ток: . По закону Ома для мгновенных значений: или где , u = i. Начальные фазовые углы тока и напряжения одинаковы, то есть совпадают по фазе (фазовый сдвиг = u – i равен нулю) и могут быть представлены двумя синусоидами с совпадающими начальными точками (рис.2.10). :
Слайд 67
u = i + j + U I Рис.2.11. Рис.2.10. u = i t i /2 Т t i, u u (2.21 ) Так как начальные фазовые углы тока и напряжения одинаковы, то на комплексной плоскости ток и напряжение представляются двумя совпадающими по направлению векторами (рис.2.11). Перейдем от синусоидальных величин к комплексным
Слайд 68
Мгновенная мощность переменного тока является величиной периодической, величина ее определяется по формуле: (2.22) Так как не может быть больше единицы, то мгновен - ная мощность, поступающая в сопротивление всегда положительна и меняется с удвоенной частотой от 0 до U m I m. Учитывая выраже - ние (2.22) выражение мгновенной мощности, можно записать: , (2.23) где U, I действующие значения напряжения и тока. Среднее значение мощности за период или просто мощность переменного тока: . (2.24) Часто эту мощность называют активной и измеряют в ваттах. Энергия, потребляемая от источника питания за время от 0 до t : (2.25)
Слайд 69
2.6.2. Ёмкость в цепи синусоидального тока а Рис.2.12. i b u ab C Электрическая ёмкость С [ Ф арад] – способ - ность элемента электрической цепи накапливать энергию в электрическом поле Подключим обкладки конденсатора к источ - н ику переменного напряжения: . (2.26) Учитывая (1.18 и 1.19) определим ток, протекающий по соедини - тельным проводам: (2.27) или, преобразуя функцию косинуса в функцию синуса (2.28) . где - амплитуда, – начальный фазовый угол тока емкостного элемента
Слайд 70
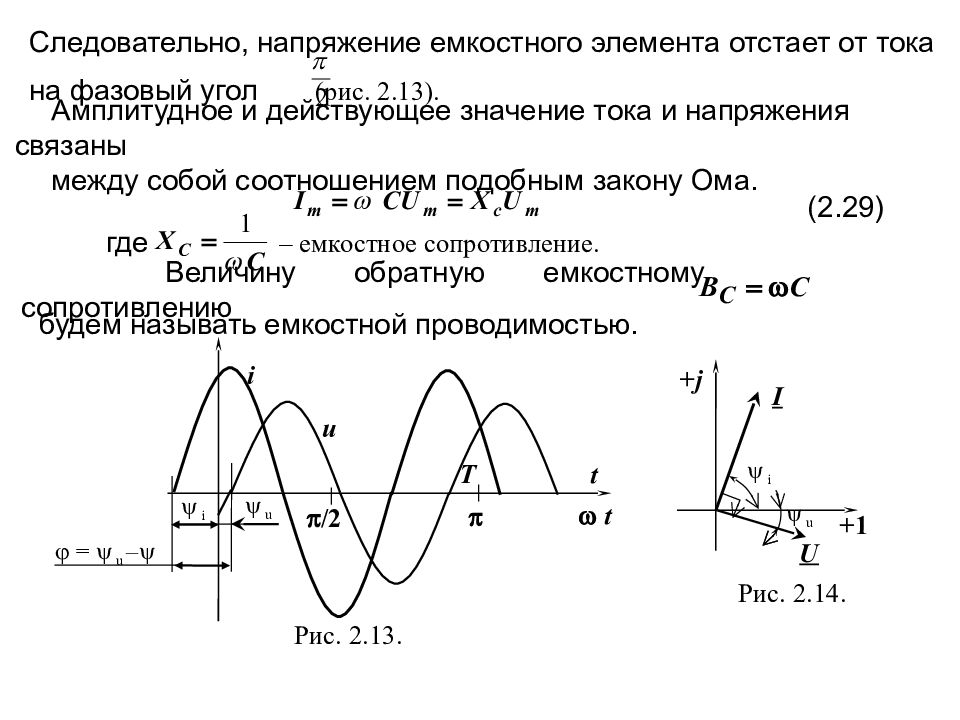
Следовательно, напряжение емкостного элемента отстает от тока на фазовый угол (рис. 2.13). Амплитудное и действующее значение тока и напряжения связаны между собой соотношением подобным закону Ома. (2.29) г де – емкостное сопротивление. Величину обратную емкостному сопротивлению будем называть емкостной проводимостью. Рис. 2.14. Рис. 2.13. i t i = u – /2 Т t u u u + j +1 i I U
Слайд 71
Перейдем от синусоидальных величин к комплексным числам: Так как начальные фазовый угол тока опережает фазовый угол напряжения на, то на комплексной плоскости ток и напряжение представляются перпендикулярными векторами (рис.2.14). На рис.2.13 представлены временные зависимости напряжения и тока емкостного элемента. Первая часть периода – напряжение увеличивается, то есть, конденсатор заряжается
Слайд 72
Направление тока совпадает с направлением внешнего напряжения. При достижении напряжением своей максимальной величины при зарядка конденсатора прекращается, ток равен нулю. Вторая часть периода – напряжение начинает уменьшаться конденсатор разряжается из-за избытка зарядов на обкладках, возникающий ток будет отрицателен. При U = 0, ток имеет отрицательный максимум, т.к. изменение заряда в этот момент происходит наиболее интенсивно. В третью четверть периода ( U <0 ) происходит заряд конденсатора в противоположном направлении, ток остается того же направления до момента прекращения зарядки конденсатора и так далее.
Слайд 73
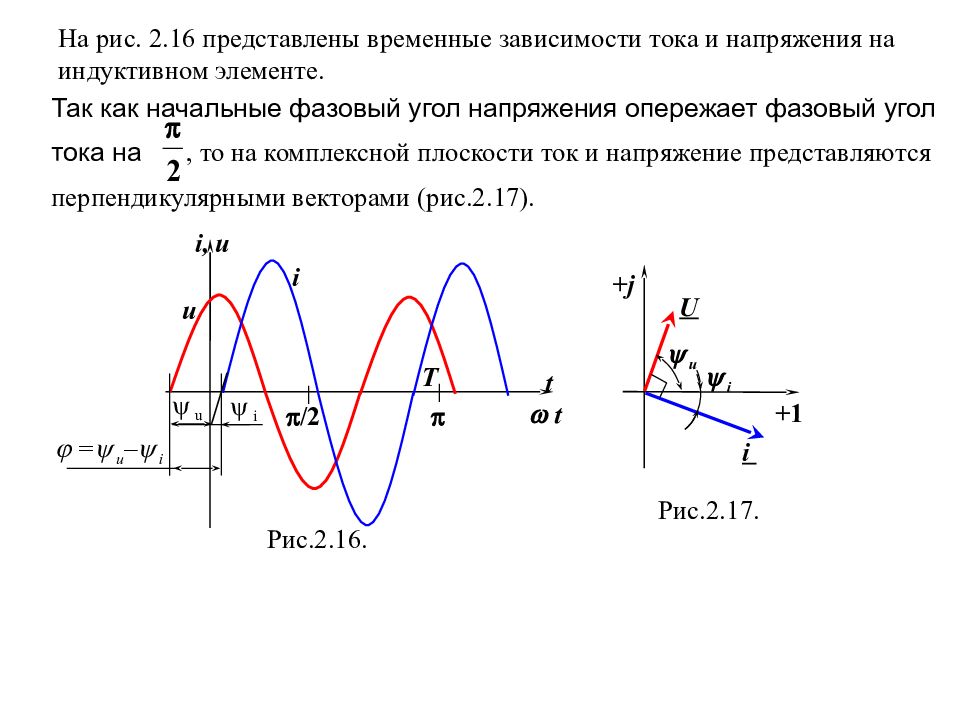
а Рис.2.15. i b u ab L 2.6.3. Индуктивность в цепи синусоидального тока Индуктивность [ Г е н ри] – способность элемента электрической цепи накапливать энергию в маг - нитном поле. Пропустим через индуктивный эле - мент переменный электрический ток . (2.31) Падение напряжения на индуктивном элементе определяется согласно формул (1.11 1.14): или, преобразуя функцию косинуса в функцию синуса, (2.33) где – амплитуда, – начальный фазовый угол падения напряжения. (2.32) Следовательно, напряжение индуктивного элемента опережает ток на фазовый угол (рис. 2.16).
Слайд 74
Амплитудное и действующее значения тока и напряжения связаны между собой соотношением подобным закону Ома. г де – индуктивное сопротивление. Величину обратную индуктивному сопротивлению будем называть индуктивной проводимостью. 2.34) 2.34) Перейдем от синусоидальных величин к комплексным числам:
Слайд 75
На рис. 2.16 представлены временные зависимости тока и напряжения на индуктивном элементе. Так как начальные фазовый угол напряжения опережает фазовый угол тока на, то на комплексной плоскости ток и напряжение представляются перпендикулярными векторами (рис.2.17). Рис.2.16. i t i = u – i /2 Т t i, u u u Рис.2.1 7. + j i +1 u i U
Слайд 76
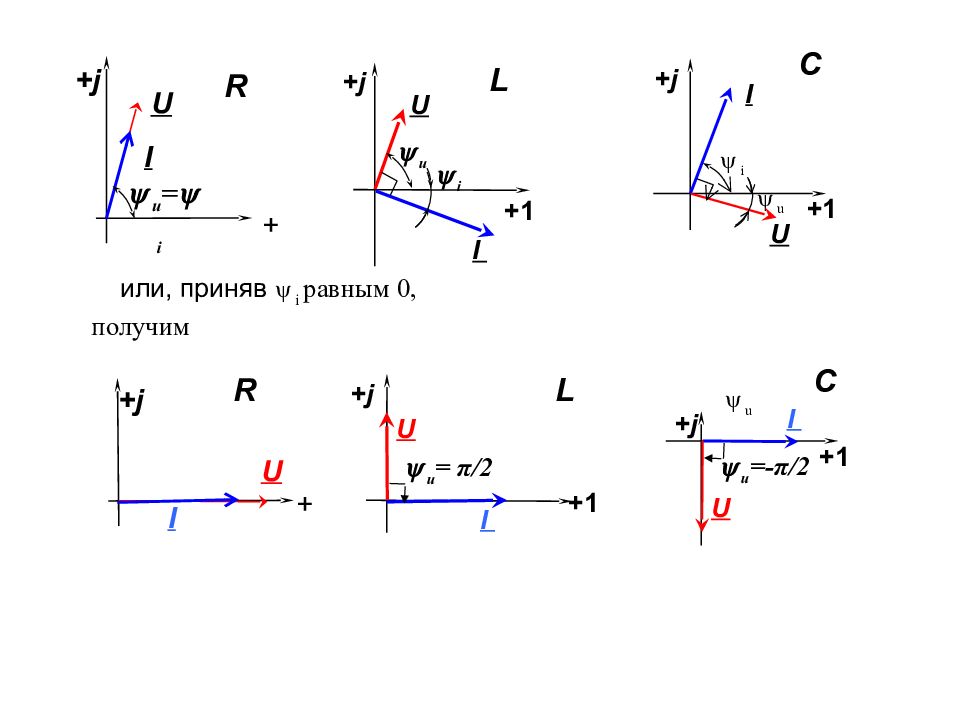
+ j i +1 u I U + j u = i + j + U I u +1 i I U C L R + j +1 u = π/2 I U + j + U I u +1 C + j I U u =-π/2 L R или, приняв i равным 0, получим
Слайд 77
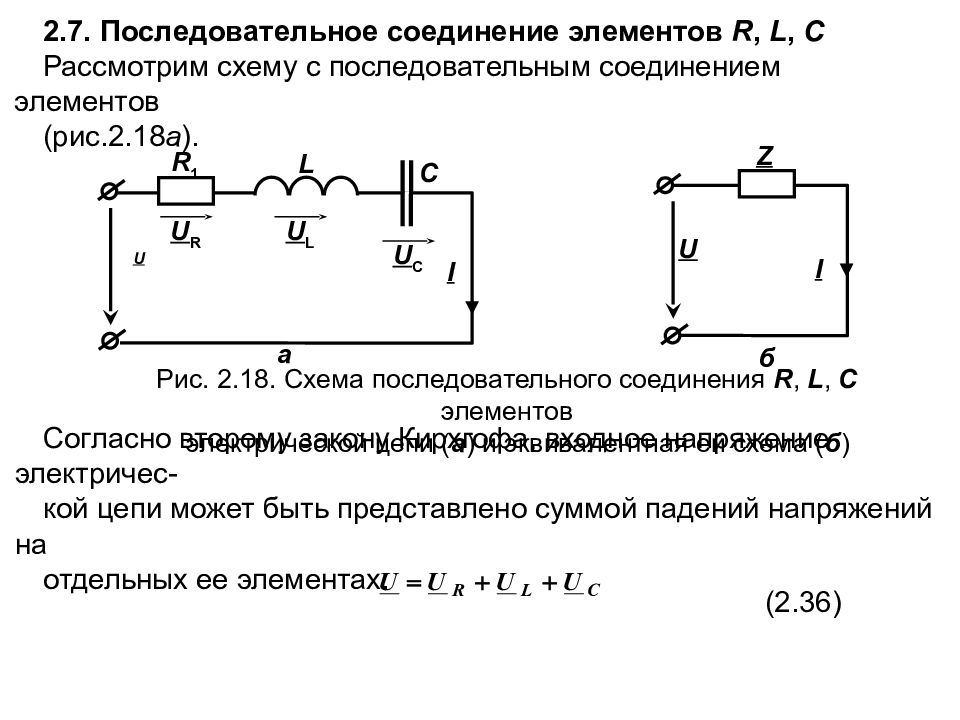
Рис. 2.18. Схема последовательного соединения R, L, C элементов электрической цепи ( а ) и эквивалентная ей схема ( б ) I U Z б I U R 1 а U C C L U R U L 2.7. Последовательное соединение элементов R, L, C Рассмотрим схему с последовательным соединением элементов (рис.2.18 а ). Согласно второму закону Кирхгофа, входное напряжение электричес - кой цепи может быть представлено суммой падений напряжений на отдельных ее элементах. (2.36)
Слайд 78
Так как соединение элементов последовательное, то ток для всех элементов цепи один. Определим падение напряжения на каждом из элементов цепи. Согласно формулам (2.21, 2.30, и 2.35) получим: Выражение (2.36) запишется: Учитывая, что и , получим: где – полное комплексное сопротивление участка электрической цепи (рис.2.18 б ). Из (2.38) получим выражение: которое определяет закон Ома в комплексной форме. . (2.37) (2.38) (2.39)
Слайд 79
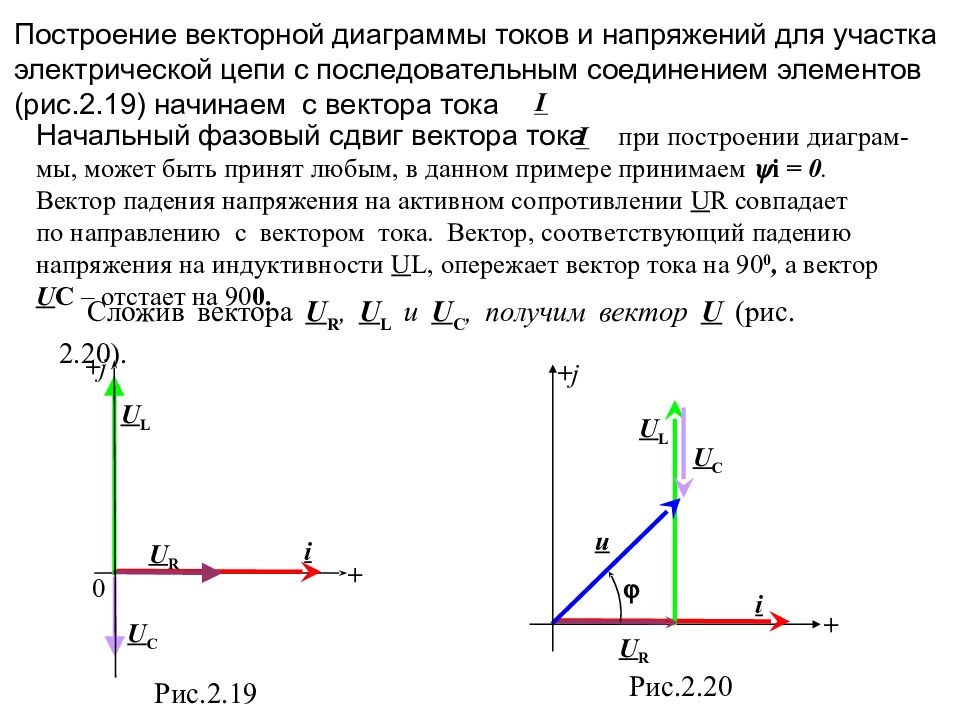
Построение векторной диаграммы токов и напряжений для участка электрической цепи с последовательным соединением элементов (рис.2.19) начинаем с вектора тока Начальный фазовый сдвиг вектора тока при построении диаграм- мы, может быть принят любым, в данном примере принимаем i = 0. Вектор падения напряжения на активном сопротивлении U R совпадает по направлению с вектором тока. Вектор, соответствующий падению напряжения на индуктивности U L, опережает вектор тока на 90 0, а вектор U C – отстает на 90 0. Сложив вектора U R, U L и U C, получим вектор U (рис. 2.20). 0 + j + U R i U L U C Рис.2.19 U R + j u i + U L U C Рис.2. 20
Слайд 80
В результате построений получается так называемый треугольник напря - жений (рис.3.7), из которого, определяется модуль полного напряжения и величина фазового сдвига между напряжением и током Если каждую сторону треугольника напряжений разделить на модуль тока, то получим подобный треугольник – треугольник сопротивлений (рис.2.21). (2.40) (2.41) + 1 +j u i U R U L – U C R X Z P Q S Рис. 2.21 Рис. 2.22 Рис. 2.23
Слайд 81
По величине угла фазового сдвига различают типы нагрузок: Если каждую сторону треугольника напряжений (рис.2.22) умножить на модуль тока, то получим подобный треугольник мощностей (рис.2.23), в котором: P = I U R – активная мощность [Вт]; Q = I ( U L – U C ) – реактивная мощность [ВАР] (вольт-ампер реактивный); S = I U – полная мощность [ВА] (вольт-ампер). В большинстве случаев при нахождении тока удобнее пользоваться показательной формой представления полного комплексного сопротивления , (2.42) - индуктивная нагрузка; - активная нагрузка; - емкостная нагрузка; - активно-индуктивная нагрузка - активно-емкостная нагрузка где –полно е сопротивлени е ; – фазовый сдвиг между напряжени ем и ток ом.
Слайд 82
Отличительной особенностью цепей содержащих индуктивные и емкостные элементы является их взаимное преобразование энергии: энергии магнитного поля индуктивного элемента в энергию электрического поля емкостного элемента и наоборот. Следовательно, возможны такие режимы работы электри- ческой цепи, при ко- торых индуктивные и емкостные элементы “будут рабо- тать друг на друга”, иными словами, взаимное преобразования энергий полей будет полным. Такие режимы работы электрической цепи получили названия резонансных режимов. +j i + U = U R U L U C Рис. 2.24 При резонансе напряжений модуль входного напряжения будет определять - ся лишь активной составляющей, а фазо - вый сдвиг между током и напряжением будет равен нулю. При этом величина тока, ограниченного лишь активной со - ставляющей сопротивления, будет макси - мальной: , .
Слайд 83
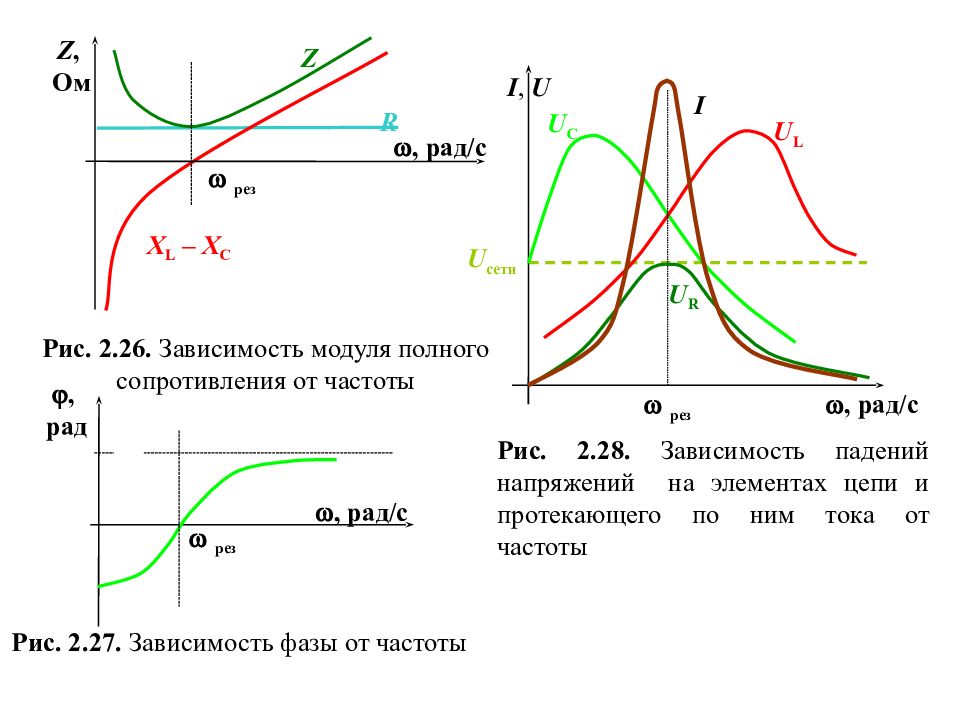
Явление резонанса в электрической цепи, содержащей последовательное соединение элементов R, L, C, может быть достигнуто изменением индук - тивности или емкости реактивных элементов, или изменением частоты питающего напряжения. На рис.2.25 представлены зависимости сопротив - лений реактивных элементов от изменения частоты. X L = L X, Ом , рад/с рез X L – X C Рис. 2.25. Зависимость реактивных сопротивлений от частоты X C = 1 ω C
Слайд 84
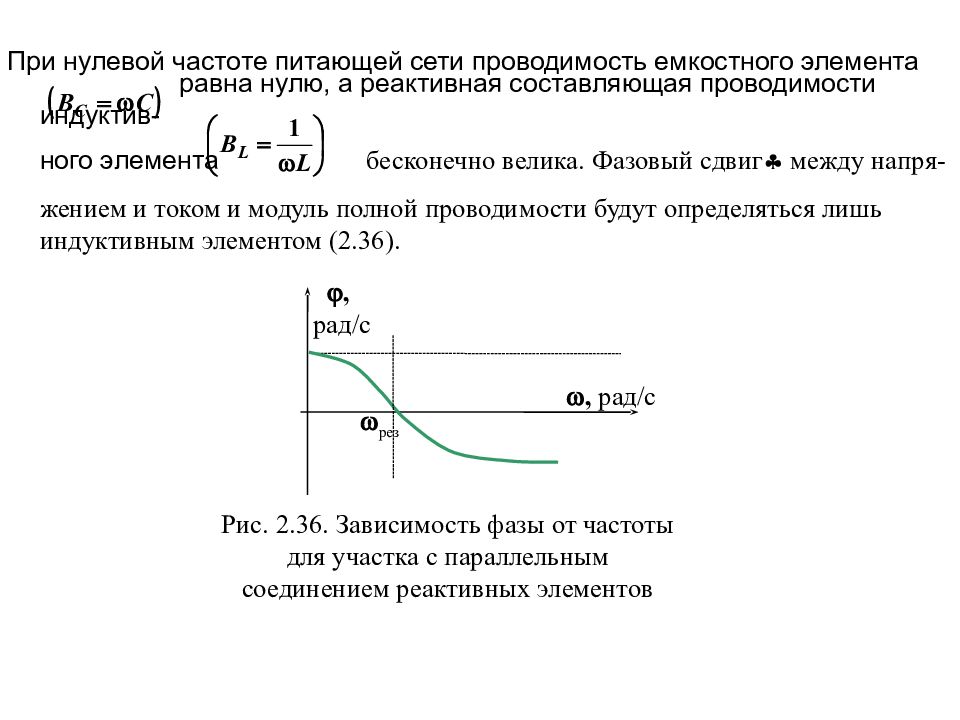
При нулевой частоте питающей сети сопротивление емкостного элемента бесконечно велико, а реактивная составляющая сопротивле - ния индуктивного элемента, напротив, равна нулю. Фазовый сдвиг между напряжением и током и модуль полного сопротивления, будут определяться только емкостным сопротивлением (рис.2.25, 2.26, 2.27). По мере увеличения частоты емкостное сопротивление будет снижаться до нуля, а сопротивление индуктивного элемента – увеличиваться. Вследствие чего будет изменяться характер нагрузки от активно емкостного до активно -индуктивного, в предельных режимах активная составляющая несуществен - на относительно сопротивления реактивного элемента. Частотные характе - ристики падений напряжений на последовательно соединенных элементах электрической цепи и характеристика тока в цепи представлены на рис.2.28 где = const, = const, = const, = const.
Слайд 85
Z, Ом , рад/с R Z X L – X C Рис. 2.26. Зависимость модуля полного сопротивления от частоты рез , рад/с рез , рад Рис. 2.27. Зависимость фазы от частоты Рис. 2.28. Зависимость падений напряжений на элементах цепи и протекающего по ним тока от частоты U сети , рад/с I рез U C U L U R I, U
Слайд 86
При ток поскольку сопротивление конденсатора бесконечно велико, следовательно,, так как бесконечно возрастает сопротивление индуктивного элемента . При ток следовательно, При резонансе реактивные составляющие напряжения взаимно скомпенси - рованы, следовательно, ток в цепи будет определяться лишь током, который протекает по активному сопротивлению под действием приложенного к нему напряжения сети
Слайд 87
2.8. Параллельное соединение элементов R, L, C Рис. 2.29. Схема параллельного соединения элементов R, L, C ( а ) и эквивалентная ей схема ( б ) а i u L R I R I L I С С i Y б u Запишем уравнение п о первому закону Кирхгофа для схемы (рис.3.29 а ): Так как соединение элементов параллельное, то напряжение для всех элементов цепи одно и то же. Определим токи в каждом из элементов цепи. Согласно формулам (2.21, 2.30, и 2.35) получим: (2.43) (2.42) Выражение (2.43) запишется: .
Слайд 88
Учитывая, что и , получим: (2.44) где – полная комплексная проводимость участка электрической цепи содержащего параллельное соединение элементов R, L, C (рис.2.29 б ). Из (2.44) получим выражение: которое определяет закон Ома в комплексной форме. (2.45) 0 +j I R U I C I L Рис. 2.30 I R +j I U +1 I C I L Рис. 2.31
Слайд 89
Построение векторной диаграммы токов и напряжений для участка электри - ческой цепи с параллельным соединением элементов начинаем с вектора – Напряжения (рис.2.30). Начальный фазовый сдвиг вектора напряжения при построении диаграммы, может быть принят любым, в данном примере принимаем U = 0. Вектор тока активного сопротивления I R совпадает по направлению с вектором падения напряжения. Вектор, соответствующий току емкости I C, опережает вектор напряжения на 90 0, а вектор тока индуктивности I L – отстает вектора напряжения на 90 0. Сложив вектора I G, I L и I C получим вектор I (рис. 2.31). В результате построений полу- чается треугольник токов (рис.2.33), исходя из которого, определяется индуктивности I L – отстает вектора напряжения и угол фазового сдвига между напряжением и током Если каждую сторону треугольника токов (рис.2.32) разделить на модуль входного напряжения, то получим подобный треугольник – треугольник проводимостей (рис.2.33). (2.46) (2.47)
Слайд 90
G B C – B L Y Рис. 2.33 I C – I L + 1 +j – I U I R Рис. 2.32 В большинстве случаев при решении задач удобнее пользоваться показатель - ной формой представления полной комплексной проводимости: где – абсолютное значение полной проводимости; (2.48) – угол сдвиг между синусоид ами напряжения и тока.
Слайд 91
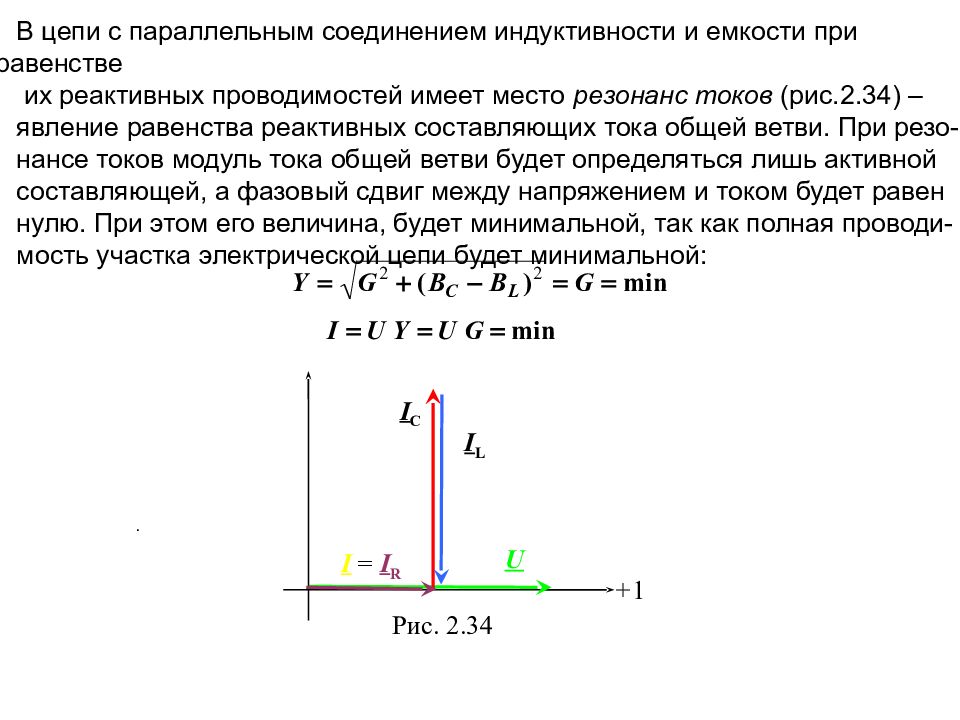
В цепи с параллельным соединением индуктивности и емкости при равенстве их реактивных проводимостей имеет место резонанс токов (рис.2.34) – явление равенства реактивных составляющих тока общей ветви. При резо - нансе токов модуль тока общей ветви будет определяться лишь активной составляющей, а фазовый сдвиг между напряжением и током будет равен нулю. При этом его величина, будет минимальной, так как полная проводи - мость участка электрической цепи будет минимальной: . U + 1 I = I R I C I L Рис. 2.34
Слайд 92
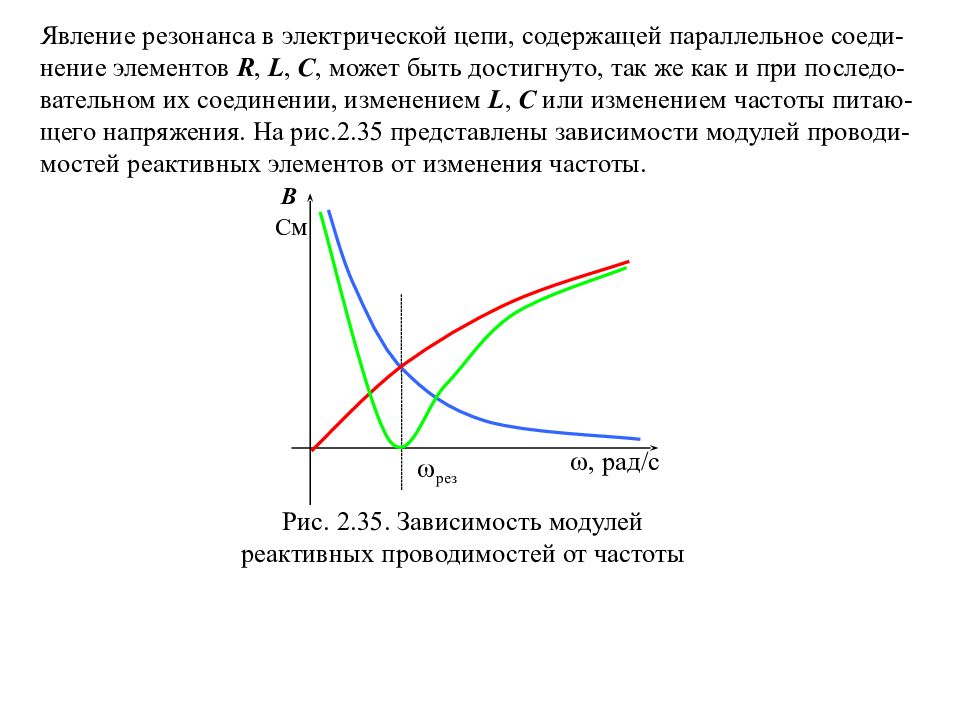
Явление резонанса в электрической цепи, содержащей параллельное соеди- нение элементов R, L, C, может быть достигнуто, так же как и при последо- вательном их соединении, изменением L, С или изменением частоты питаю- щего напряжения. На рис.2.35 представлены зависимости модулей проводи- мостей реактивных элементов от изменения частоты. Рис. 2.35. Зависимость модулей реактивных проводимостей от частоты B C м , рад/с рез
Слайд 93
При нулевой частоте питающей сети проводимость емкостного элемента равна нулю, а реактивная составляющая проводимости индуктив - ного элемента бесконечно велика. Фазовый сдвиг между напря- жением и током и модуль полной проводимости будут определяться лишь индуктивным элементом (2.36). Рис. 2.36. Зависимость фазы от частоты для участка с параллельным соединением реактивных элементов , рад/с рез , рад/с
Слайд 94
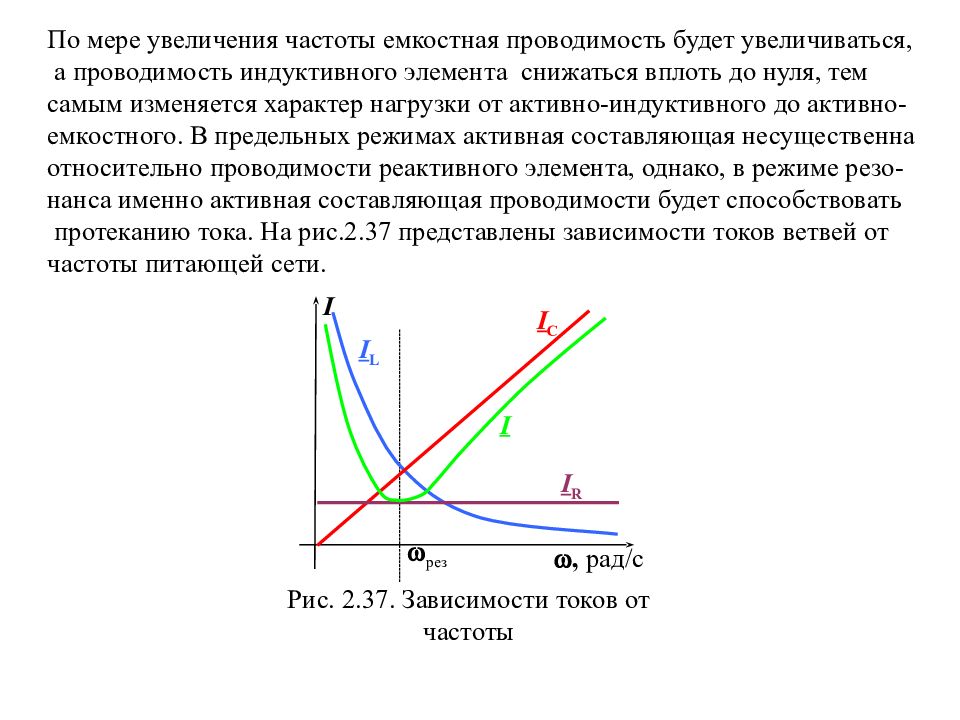
По мере увеличения частоты емкостная проводимость будет увеличиваться, а проводимость индуктивного элемента снижаться вплоть до нуля, тем самым изменяется характер нагрузки от активно-индуктивного до активно- емкостного. В предельных режимах активная составляющая несущественна относительно проводимости реактивного элемента, однако, в режиме резо- нанса именно активная составляющая проводимости будет способствовать протеканию тока. На рис.2.37 представлены зависимости токов ветвей от частоты питающей сети. I R Рис. 2.37. Зависимости токов от частоты I , рад/с рез I L I C I
Слайд 95
2.9.1. Мгновенная мощность, полная мощность Мгновенная мощность – мощность участка электрической цепи, определя - емая произведением мгновенных значений протекающего по нему тока i и приложенного к нему напряжения u : s = u i [ В ольт А мпер]. (2.49) Пусть ток опережает напряжения по фазе на угол : Тогда мгновенная мощность переменного тока : (2.50) где I, U – действующие значения тока и напряжения.
Слайд 96
В данной формуле (2.34) первое слагаемое является постоянным для данной цепи и не зависит от времени. Это слагаемое принято называть активной со- ставляющей (активной мощностью). Второе слагаемое характеризует обмен энергиями между источником и потре- бителем. Такой процесс возможен лишь при наличии реактивных элементов в цепи, способных накапливать энергию в виде полей и отдавать ее обратно в цепь. Поэтому второе слагаемое принято называть реактивной составляющей мощности (реактивной мощностью). Полная мощность: S = P + j ( QL – QC ) (2.51)
Слайд 97
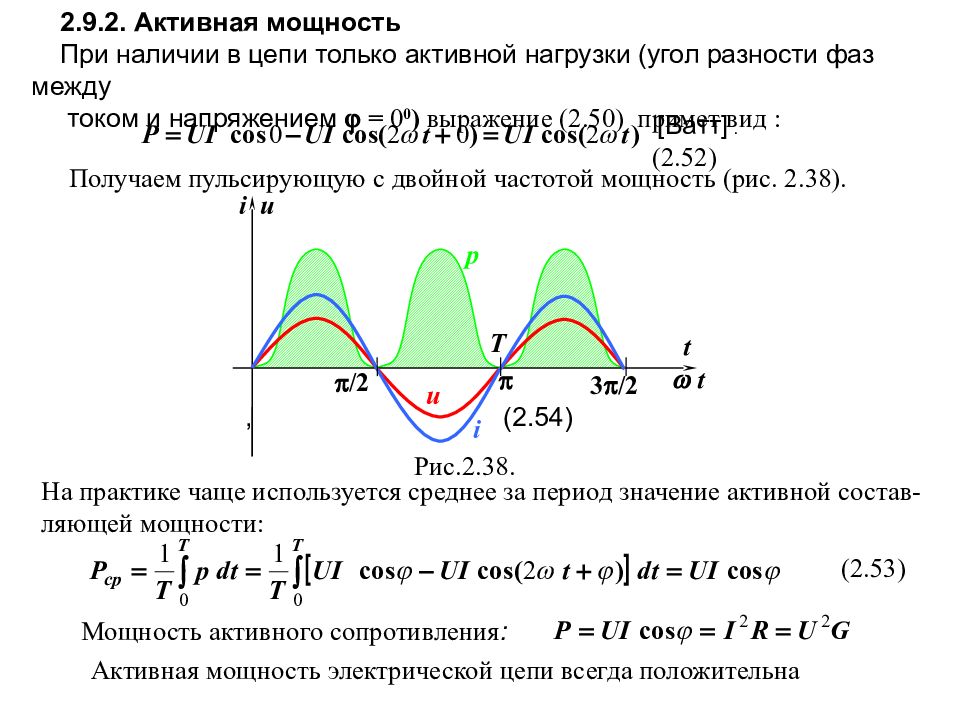
2.9.2. Активная мощность При наличии в цепи только активной нагрузки (угол разности фаз между током и напряжением = 0 0 ) выражение (2.50) примет вид : [Ватт]. (2.52) Получаем пульсирующую с двойной частотой мощность (рис. 2.38). Рис.2. 38. t i 3 /2 /2 t i u u р Т На практике чаще используется среднее за период значение активной состав- ляющей мощности: (2.53) Мощность активного сопротивления : , (2.54) Активная мощность электрической цепи всегда положительна
Слайд 98
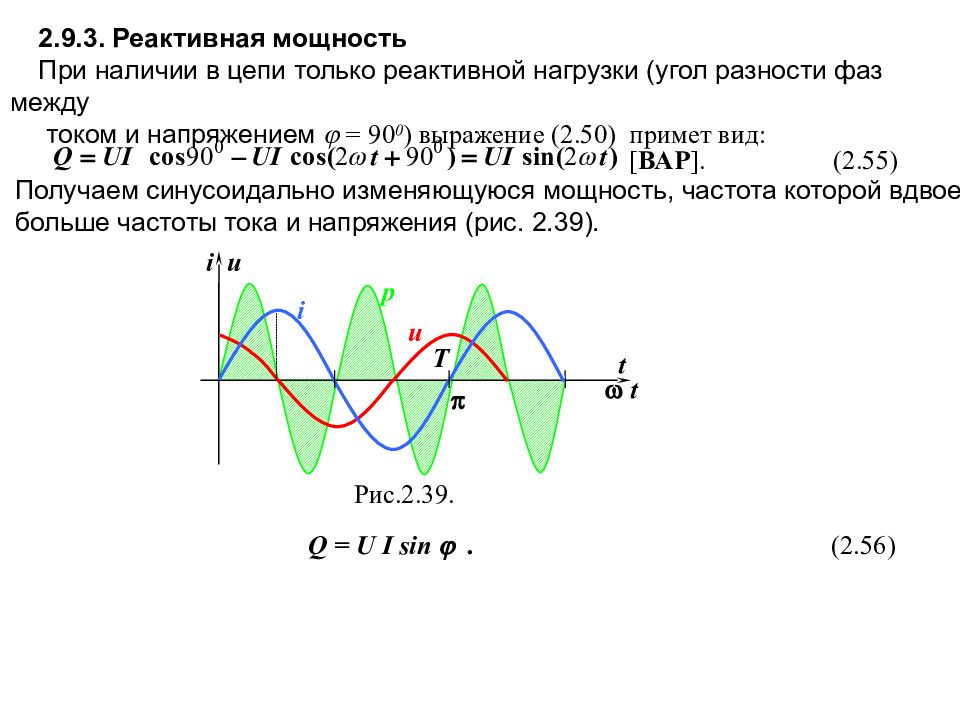
2.9.3. Реактивная мощность При наличии в цепи только реактивной нагрузки (угол разности фаз между током и напряжением = 90 0 ) выражение (2.50) примет вид: Получаем синусоидально изменяющуюся мощность, частота которой вдвое больше частоты тока и напряжения (рис. 2.39). [ ВАР ]. (2.55) Рис.2. 39. t i t i u u р Т Q = U I sin . (2.56)
Слайд 99
Реактивная мощность индуктивного элемента : где – индуктивное сопротивление; Реактивная мощность емкостного элемента : где – емкостное сопротивление; – емкостная проводимость. (2.57) – индуктивная проводимость (2.58)
Слайд 100
2.9.4. Коэффициент мощности Рис. 2.40. P = UI cos Q = UI sin S = UI Составляющие мощностей могут быть сведены к треугольнику мощностей (рис.2.40). Важное практическое значение имеет с os – коэффициент мощ- ности, определяющий долю активной энергии, идущей на выполнение полез- ной работы (получение тепловой, механической и других энергий) к полной мощности, потребляемой из сети: . (2.59) Чем выше коэффициент мощности того или иного электротехнического устройства, тем экономичнее его работа.
Слайд 102
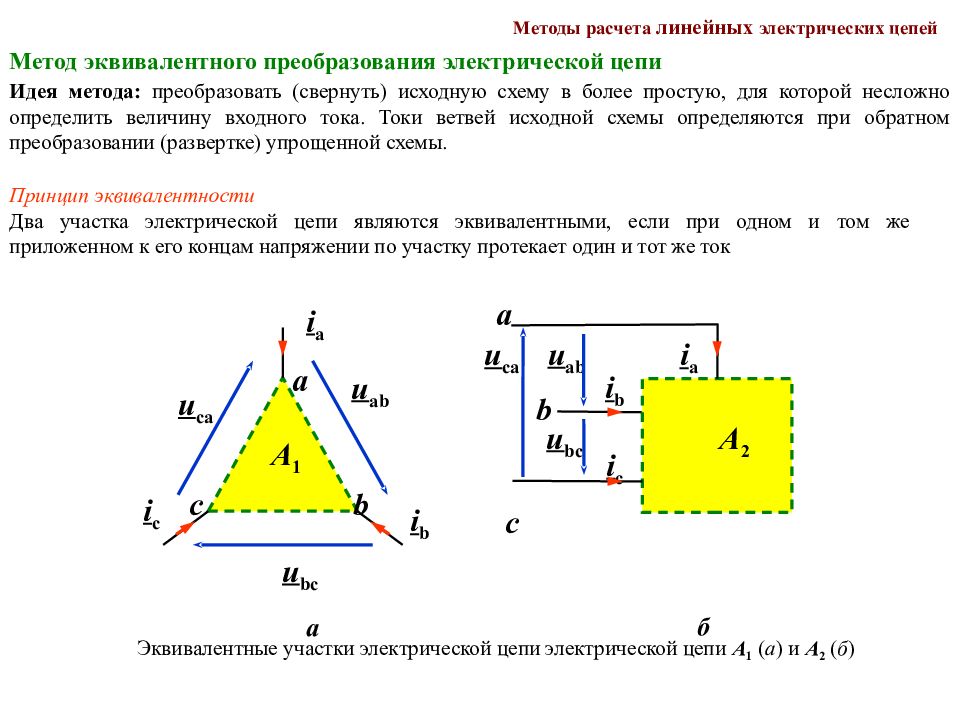
Методы расчета линейных электрических цепей Метод эквивалентного преобразования электрической цепи Идея метода: преобразовать (свернуть) исходную схему в более простую, для которой несложно определить величину входного тока. Токи ветвей исходной схемы определяются при обратном преобразовании (развертке) упрощенной схемы. П ринцип эквивалентности Два участка электрической цепи являются эквивалентными, если при одном и том же приложенном к его концам напряжении по участку протекает один и тот же ток i a u ab i b i c u ca u bc a b с А 1 i a u ab i b i c u ca u bc a b с А 2 Эквивалентные участки электрической цепи электрической цепи А 1 ( а ) и А 2 ( б ) а б
Слайд 103
Согласно второму закону Кирхгофа д ля схемы а входное напряжение исходной схемы равно сумме падений напряжений на элементах . Для схемы б : Исходя из сопоставления этих формул, эквивалентное сопротивление последовательно соединенных элементов: Эквивалентное сопротивление последовательного соединения равно сумме сопротивлений последовательно соединенных резистивных элементов. Метод эквивалентного преобразования электрической цепи Последовательное соединение пассивных элементов Особенность последовательного соединения элементов: ток, протекающий по последовательно соединенным элементам один и тот же. Схема последовательного соединения резистивных элементов электрической цепи ( а ) и эквивалентная ей схема ( б ) I R 1 U R 2 R n а I U R Э б
Слайд 104
Согласно первому закону Кирхгофа: По закону Ома токи ветвей, могут быть представлены как: ; ; где G n – проводимость n -ой ветви. Подставив полученные выражения в уравнение для токов и выполнив элементарные преобразования, получим: Таким образом, эквивалентная проводимость участка электрической цепи, содержащего параллельное соединение элементов, определяется суммой проводимостей каждого элемента в отдельности. Метод эквивалентного преобразования электрической цепи Параллельное соединение пассивных участков электрической цепи Особенность параллельного соединения элементов: напряжение на зажимах параллельно соединенных элементов одно и тот же. Схема параллельного соединения резистивных элементов электрической цепи ( а ) и эквивалентная ей схема ( б ) I G 1 U G 2 G n а I U G Э б
Слайд 105
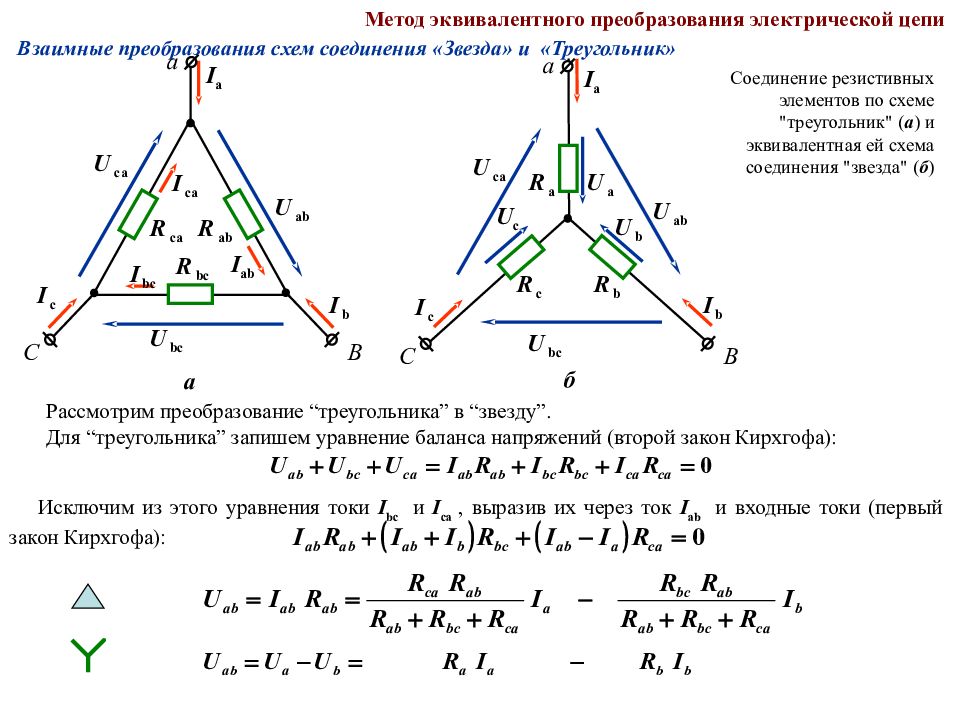
Метод эквивалентного преобразования электрической цепи Взаимные преобразования схем соединения «Звезда» и «Треугольник» а R ab R ca R bc U ab U ca U bc I b I a I c I ab I ca I bc а В С Соединение резистивных элементов по схеме "треугольник" ( а ) и эквивалентная ей схема соединения "звезда" ( б ) б U ab U ca U bc I b I a I c R b R a R c U b U a U c а В С Рассмотрим преобразование “треугольника” в “звезду”. Для “треугольника” запишем уравнение баланса напряжений (второй закон Кирхгофа): Исключим из этого уравнения токи I b с и I са, выразив их через ток I ab и входные токи (первый закон Кирхгофа):
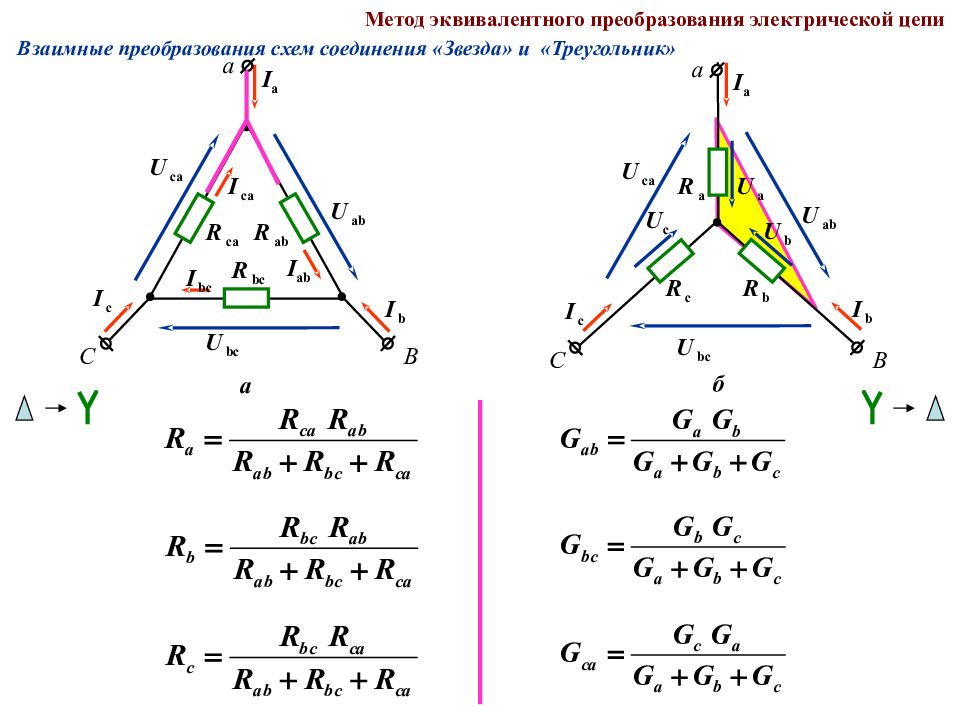
Слайд 106
Метод эквивалентного преобразования электрической цепи Взаимные преобразования схем соединения «Звезда» и «Треугольник» а R ab R ca R bc U ab U ca U bc I b I a I c I ab I ca I bc а В С б U ab U ca U bc I b I a I c R b R a R c U b U a U c а В С
Слайд 107
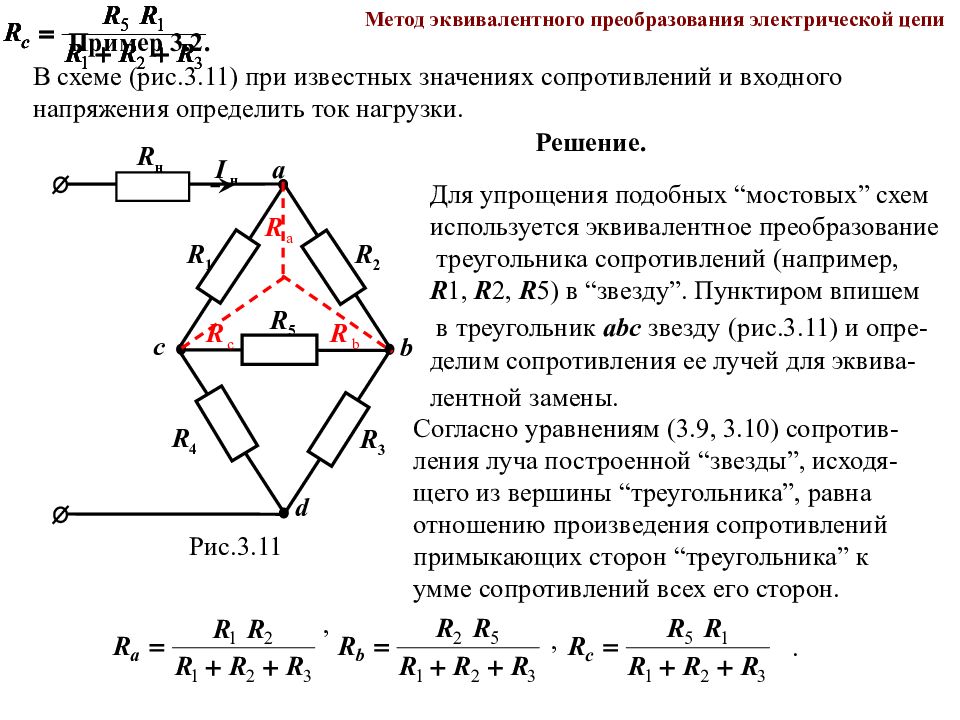
Метод эквивалентного преобразования электрической цепи Пример 3.2. В схеме (рис.3.11) при известных значениях сопротивлений и входного напряжения определить ток нагрузки. Решение. Для упрощения подобных “мостовых” схем используется эквивалентное преобразование треугольника сопротивлений (например, R 1, R 2, R 5) в “звезду”. Пунктиром впишем в треугольник а bc звезду (рис.3.11) и опре- делим сопротивления ее лучей для эквива- лентной замены. Согласно уравнениям (3.9, 3.10) сопротив- ления луча построенной “звезды”, исходя- щего из вершины “треугольника”, равна отношению произведения сопротивлений примыкающих сторон “треугольника” к умме сопротивлений всех его сторон. , , . I н R 2 R 3 R 1 R 4 R 5 R н а b с d R a R b R c Рис.3.11
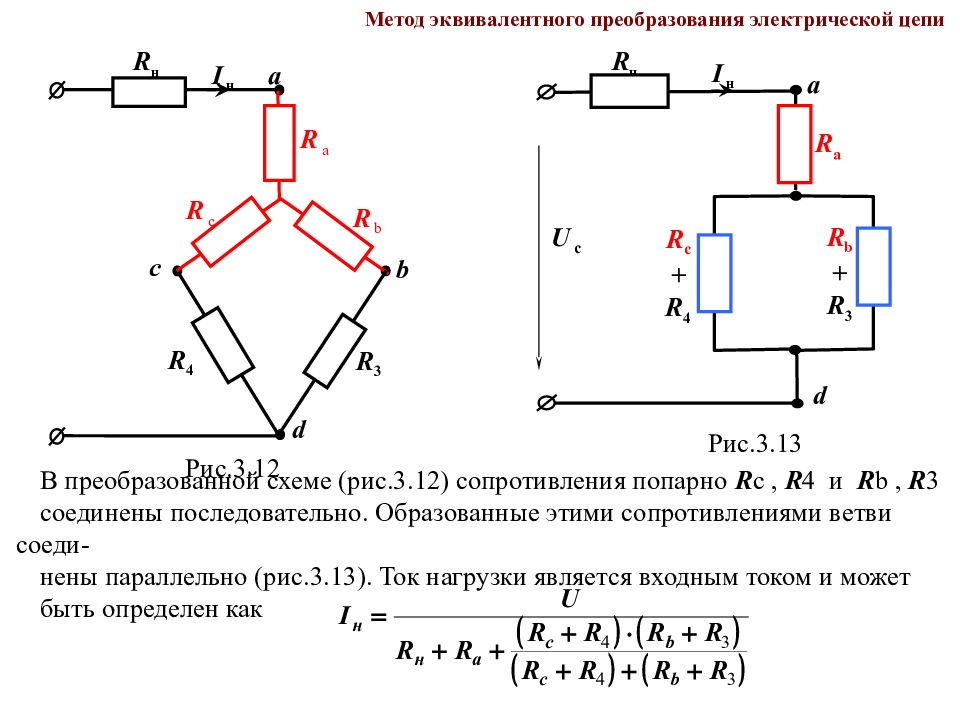
Слайд 108
Метод эквивалентного преобразования электрической цепи I н R 3 R 4 R н а b с d R a R b R c Рис.3.12 В преобразованной схеме (рис.3.12) сопротивления попарно R c, R 4 и R b, R 3 соединены последовательно. Образованные этими сопротивлениями ветви соеди- нены параллельно (рис.3.13). Ток нагрузки является входным током и может быть определен как R c + R 4 Рис.3.13 I н R н а d R a U c R b + R 3
Слайд 109
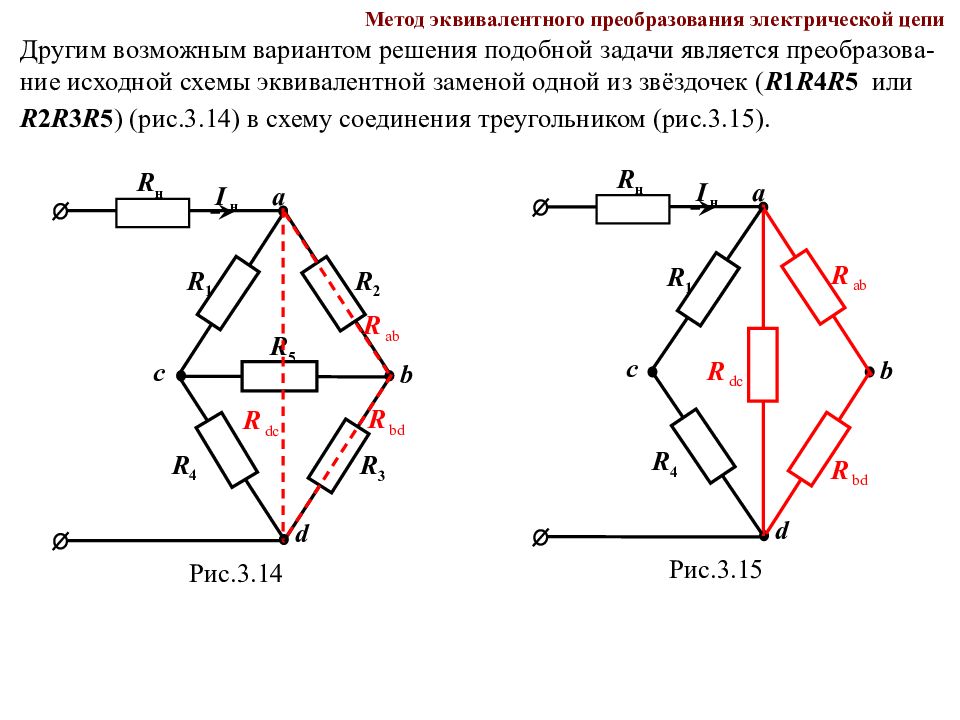
Метод эквивалентного преобразования электрической цепи Другим возможным вариантом решения подобной задачи является преобразова- ние исходной схемы эквивалентной заменой одной из звёздочек ( R 1 R 4 R 5 или R 2 R 3 R 5 ) (рис.3.14) в схему соединения треугольником (рис.3.15). I н R 2 R 3 R 1 R 4 R 5 R н а b с d R ab R bd R dc Рис.3.1 4 I н R 1 R 4 R н а b с d R ab R bd R dc Рис.3.15
Слайд 110
Метод эквивалентного преобразования электрической цепи Пример 3.1. При заданных параметрах электрической цепи: значениях индуктивностей, ёмкостей и активных сопротивлений, а так же параметрах питающей сети: напряжении и частоте, определить токи в ветвях электрической цепи. Представим последовательные соединения сопротивлений в ветвях схемы их полными комплексными сопротивлениями (рис.3.4) Рис. 3.4. Схема электрической цепи u L 2 С 1 R 1 L 1 R 2 С 2 ; ;
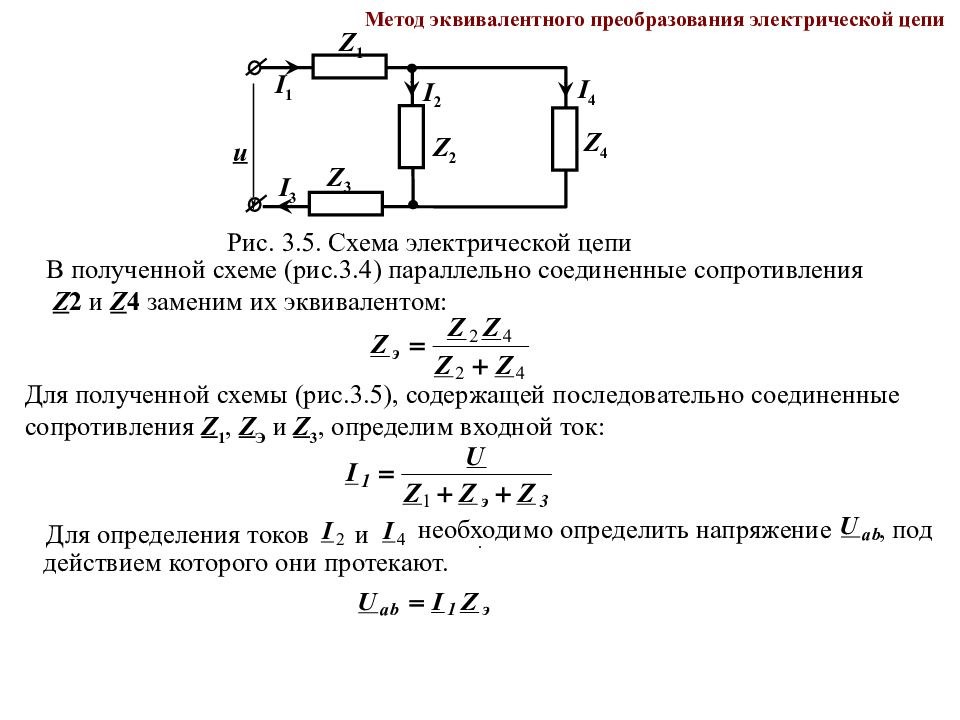
Слайд 111
Метод эквивалентного преобразования электрической цепи . Рис. 3. 5. Схема электрической цепи u Z 4 Z 1 Z 2 I 4 I 2 I 1 Z 3 I 3 В полученной схеме (рис.3.4) параллельно соединенные сопротивления Z 2 и Z 4 заменим их эквивалентом: Для полученной схемы (рис.3.5), содержащей последовательно соединенные сопротивления Z 1, Z Э и Z 3, определим входной ток: Для определения токов и необходимо определить напряжение, под действием которого они протекают.
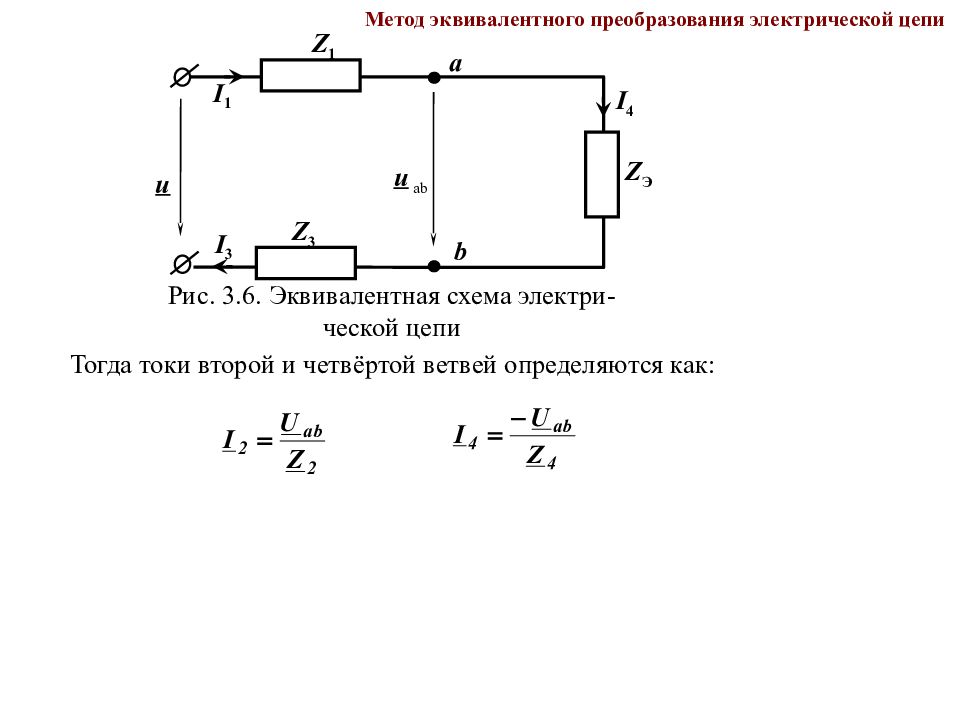
Слайд 112
Метод эквивалентного преобразования электрической цепи Рис. 3. 6. Эквивалентная схема электри - ческой цепи Z 1 u Z Э I 4 I 1 Z 3 I 3 a b u ab Тогда токи второй и четвёртой ветвей определяются как:
Слайд 113
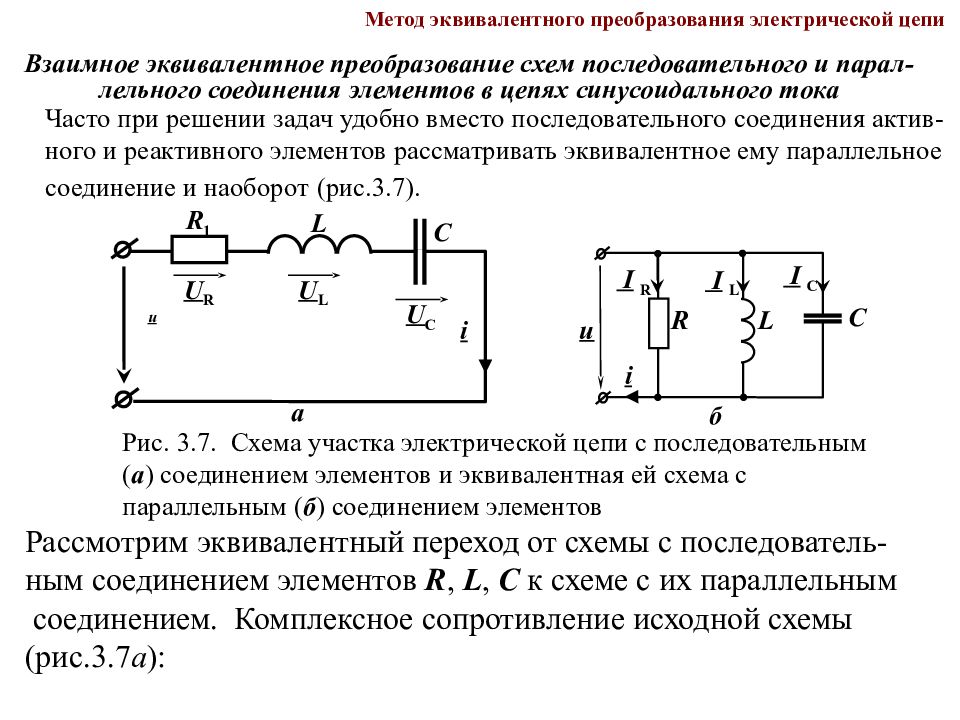
Метод эквивалентного преобразования электрической цепи Взаимное эквивалентное преобразование схем последовательного и парал- лельного соединения элементов в цепях синусоидального тока Часто при решении задач удобно вместо последовательного соединения актив- ного и реактивного элементов рассматривать эквивалентное ему параллельное соединение и наоборот (рис.3.7). Рис. 3.7. Схема участка электрической цепи с последовательным ( а ) соединением элементов и эквивалентная ей схема с параллельным ( б ) соединением элементов б i u L R I R I L I С С i u R 1 а U C C L U R U L Рассмотрим эквивалентный переход от схемы с последователь- ным соединением элементов R, L, C к схеме с их параллельным соединением. Комплексное сопротивление исходной схемы (рис.3.7 а ):
Слайд 114
Метод эквивалентного преобразования электрической цепи Эквивалентная ей проводимость: (3.4) Комплексная проводимость и сопротивление эквивалентной схемы (рис.3.7 б ): , (3.5) . (3.6) Формулы перехода от последовательного соединения к параллельному (3.7) и обратно (3.8) получаются из сопоставления выражений для сопротивлений (3.3) и (3.6) и проводимостей (3.5) и (3.6) (3.7) (3.8)
Слайд 115
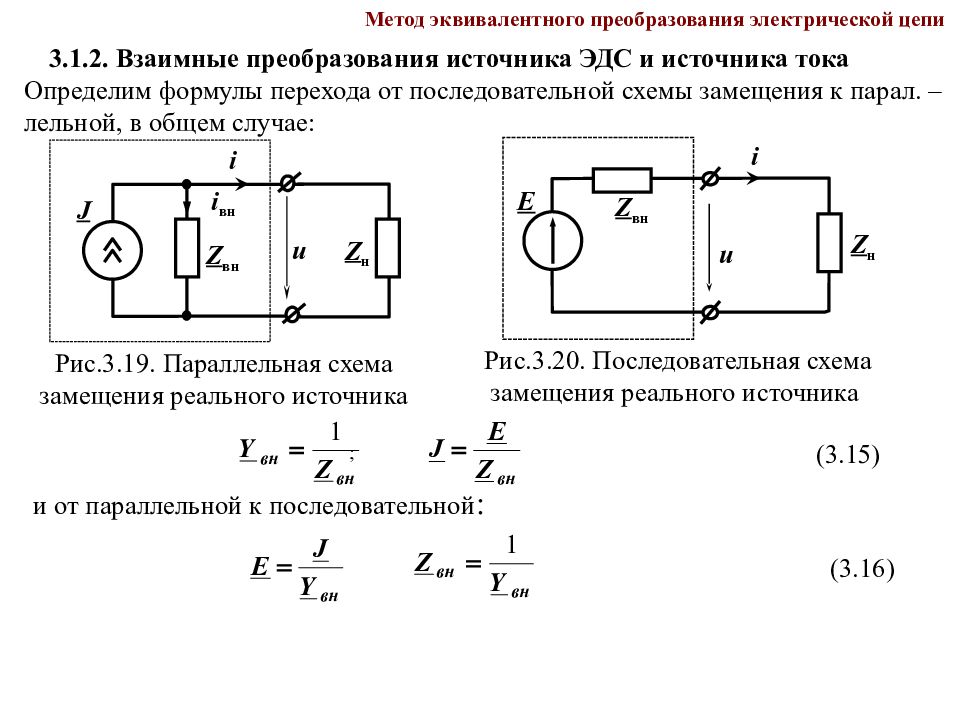
Метод эквивалентного преобразования электрической цепи 3.1.2. Взаимные преобразования источника ЭДС и источника тока Рис.3.19. Параллельная схема замещения реального источника i Z вн J u i вн Z н Рис.3.20. Последовательная схема замещения реального источника i u Z вн E Z н Определим формулы перехода от последовательной схемы замещения к парал. – лельной, в общем случае: ; (3.15) и от параллельной к последовательной : (3.16)
Слайд 116
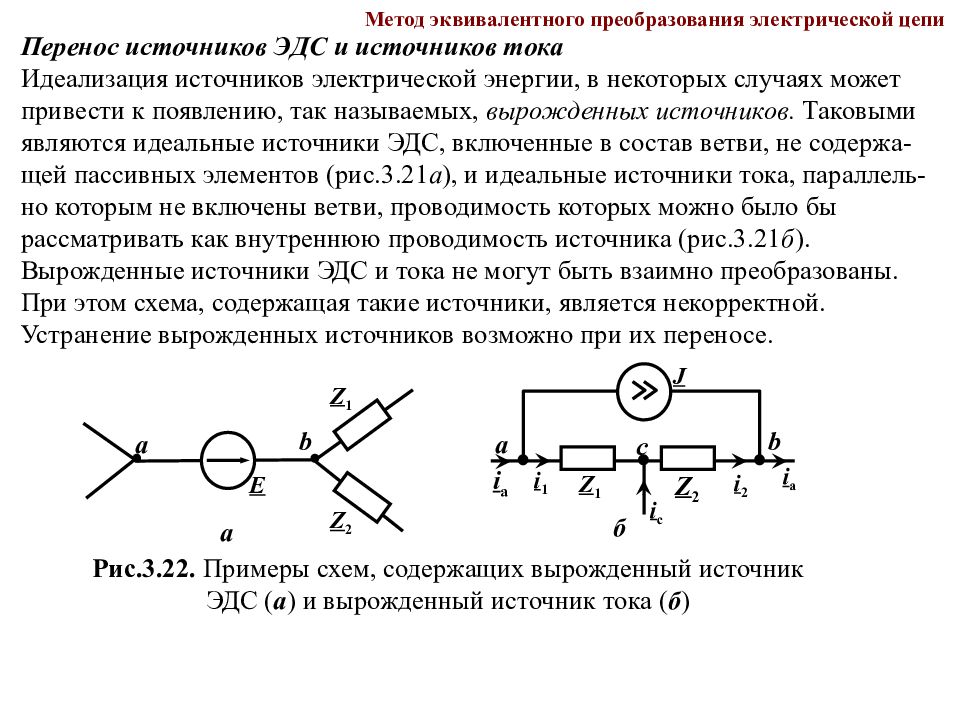
Метод эквивалентного преобразования электрической цепи Перенос источников ЭДС и источников тока Идеализация источников электрической энергии, в некоторых случаях может привести к появлению, так называемых, вырожденных источников. Таковыми являются идеальные источники ЭДС, включенные в состав ветви, не содержа-щей пассивных элементов (рис.3.21 а ), и идеальные источники тока, параллель- но которым не включены ветви, проводимость которых можно было бы рассматривать как внутреннюю проводимость источника (рис.3.21 б ). Вырожденные источники ЭДС и тока не могут быть взаимно преобразованы. При этом схема, содержащая такие источники, является некорректной. Устранение вырожденных источников возможно при их переносе. Рис.3.22. Примеры схем, содержащих вырожденный источник ЭДС ( а ) и вырожденный источник тока ( б ) a Z 1 а E b Z 2 б i а Z 1 J а b с Z 2 i с i а i 1 i 2
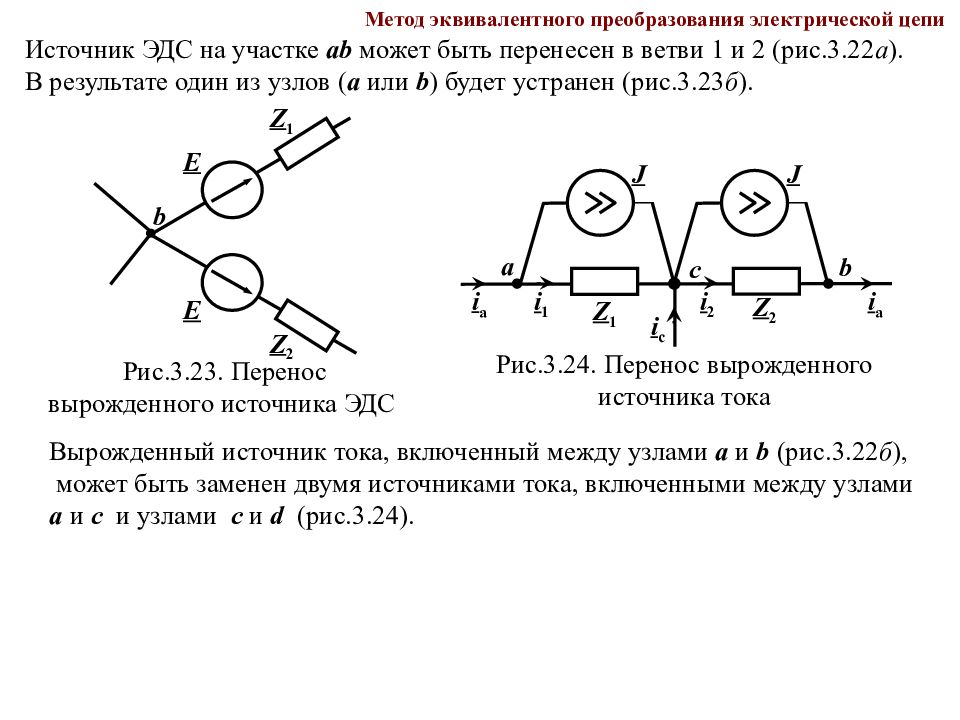
Слайд 117
Метод эквивалентного преобразования электрической цепи Рис.3.24. Перенос вырожденного источника тока i 1 i а i а Z 1 J а b с Z 2 i с J i 2 Рис.3.23. Перенос вырожденного источника ЭДС Z 1 b Z 2 E E Источник ЭДС на участке а b может быть перенесен в ветви 1 и 2 (рис.3.22 а ). В результате один из узлов ( а или b ) будет устранен (рис.3.23 б ). Вырожденный источник тока, включенный между узлами а и b (рис.3.22 б ), может быть заменен двумя источниками тока, включенными между узлами а и с и узлами с и d (рис.3.24).
Слайд 118
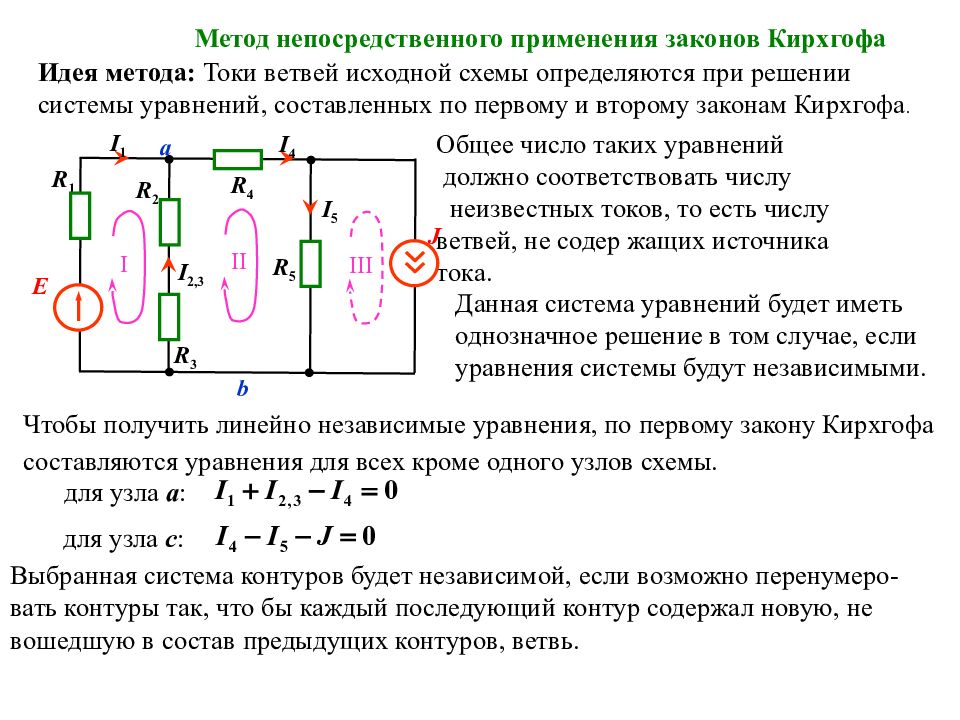
Данная система уравнений будет иметь однозначное решение в том случае, если уравнения системы будут независимыми. Метод непосредственного применения законов Кирхгофа Идея метода: Токи ветвей исходной схемы определяются при решении системы уравнений, составленных по первому и второму законам Кирхгофа. Общее число таких уравнений должно соответствовать числу неизвестных токов, то есть числу ветвей, не содер жащих источника тока. Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляются уравнения для всех кроме одного узлов схемы. Выбранная система контуров будет независимой, если возможно перенумеро- вать контуры так, что бы каждый последующий контур содержал новую, не вошедшую в состав предыдущих контуров, ветвь. для узла а : для узла с : R 1 E J а I 5 I 4 I 1 R 2 R 4 R 5 R 3 b I 2,3 II I II I
Слайд 119
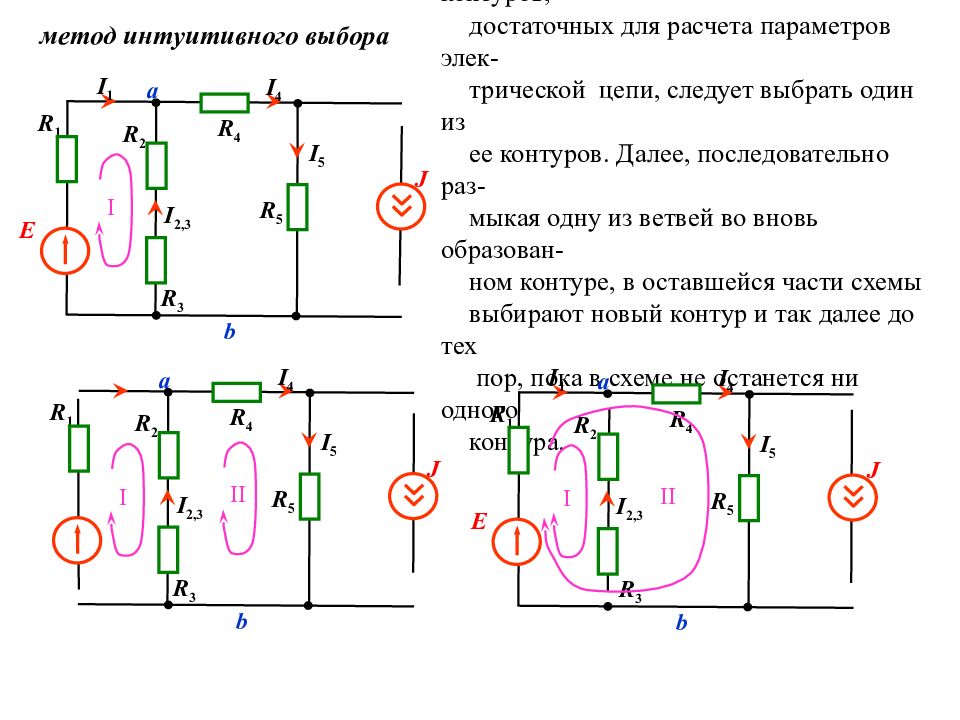
Для определения независимых контуров, достаточных для расчета параметров элек- трической цепи, следует выбрать один из ее контуров. Далее, последовательно раз- мыкая одну из ветвей во вновь образован- ном контуре, в оставшейся части схемы выбирают новый контур и так далее до тех пор, пока в схеме не останется ни одного контура. R 1 E J а I 5 I 4 I 1 R 2 R 4 R 5 R 3 b I 2,3 I R 1 J а I 5 I 4 R 2 R 4 R 5 R 3 b I 2,3 II I метод интуитивного выбора R 1 E J а I 5 I 4 I 1 R 2 R 4 R 5 R 3 b I 2,3 II I
Слайд 120
Выбор независимых контуров I III II b 5 1 6 2 4 с a I II b 5 1 2 4 с a д ля контура I I метод формализованного выбора Для выбора независимых контуров согласно данному методу по исходной схеме строится вспомо - гательная схема – граф электрической цепи, вершины которого, являющиеся узлами исходной схемы, соединены ветвями – линиями, соответствующими ветвям схемы, но не содержащими эле - ментов. Далее строится дерево графа – вспомогательная схема, содержащая все узлы графа, соеди - ненные между собой ветвями, но не содержащая контуров, то есть между любой парой вершин существует лишь единственный путь. Независимые контуры получаются добавлением к дереву графа оставшихся ветвей. для контура I
Слайд 121
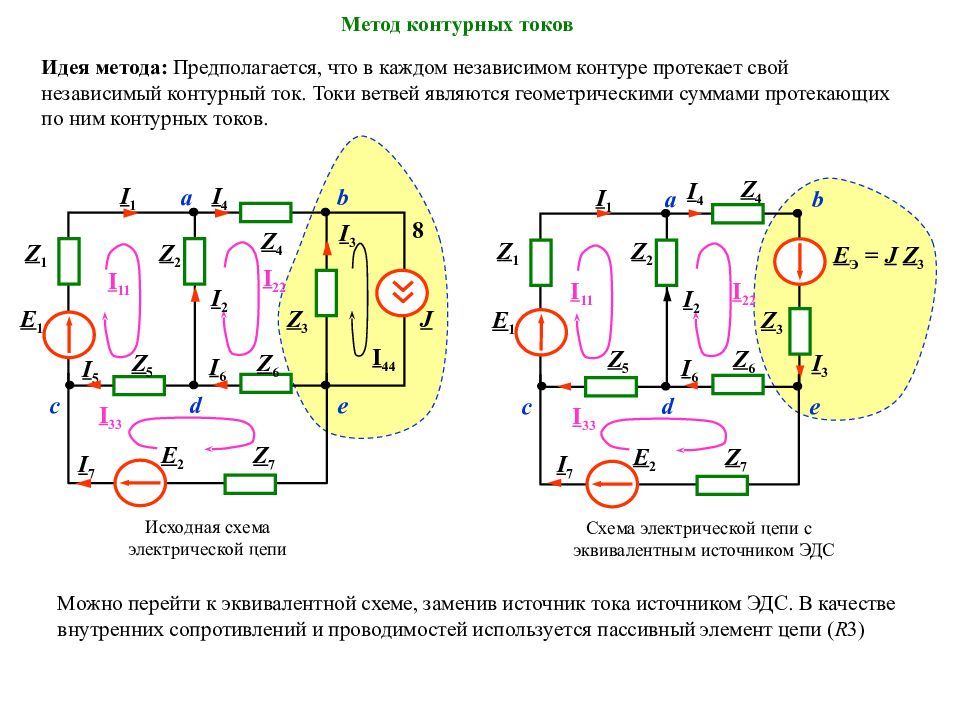
Метод контурных токов Идея метода: Предполагается, что в каждом независимом контуре протекает свой независимый контурный ток. Токи ветвей являются геометрическими суммами протекающих по ним контурных токов. Можно перейти к эквивалентной схеме, заменив источник тока источником ЭДС. В качестве внутренних сопротивлений и проводимостей используется пассивный элемент цепи ( R 3) a b d c e I 4 Исходная схема электрической цепи I 11 Z 3 Z 1 E 1 J Z 2 Z 4 I 3 I 1 I 2 Z 7 E 2 I 6 I 5 Z 6 Z 5 I 7 8 I 22 I 33 I 44 Схема электрической цепи с эквивалентным источником ЭДС а b I 4 Z 4 I 1 Z 1 I 33 d c e Z 3 E 1 Z 2 I 3 I 2 Z 7 E 2 I 6 Z 6 Z 5 E Э = J Z 3 I 22 I 7 I 11
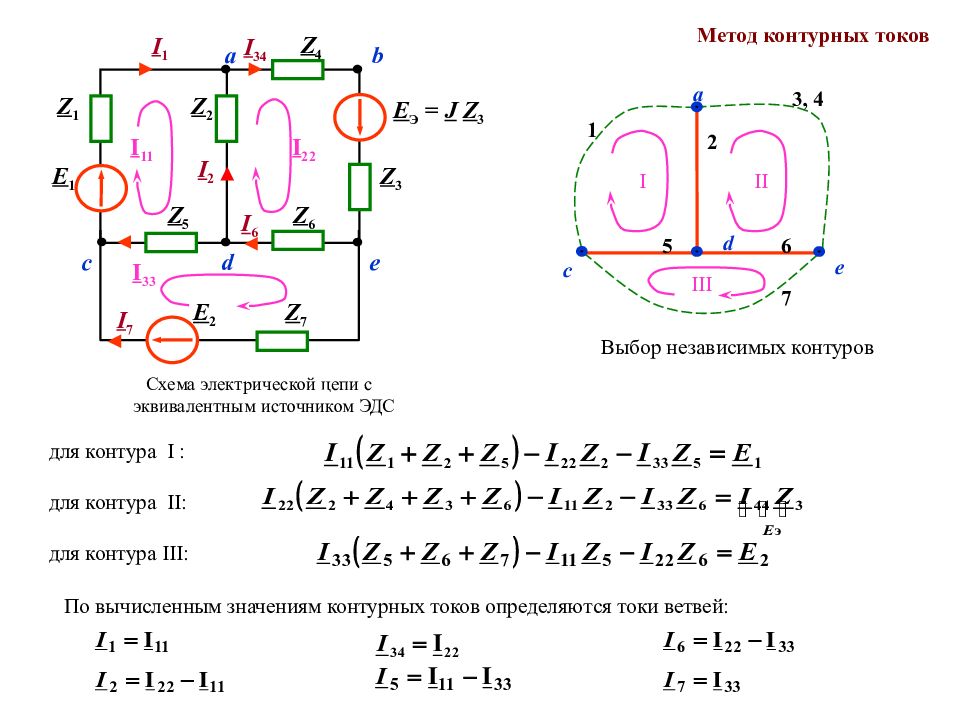
Слайд 122
Схема электрической цепи с эквивалентным источником ЭДС а b I 34 Z 4 I 1 Z 1 I 33 d c e Z 3 E 1 Z 2 I 2 Z 7 E 2 I 6 Z 6 Z 5 E Э = J Z 3 I 22 I 7 I 11 Метод контурных токов I 1 2 3, 4 5 6 7 II III Выбор независимых контуров c а d e для контура I : для контура II : д ля контура III : По вычисленным значениям контурных токов определяются токи ветвей :
Слайд 123
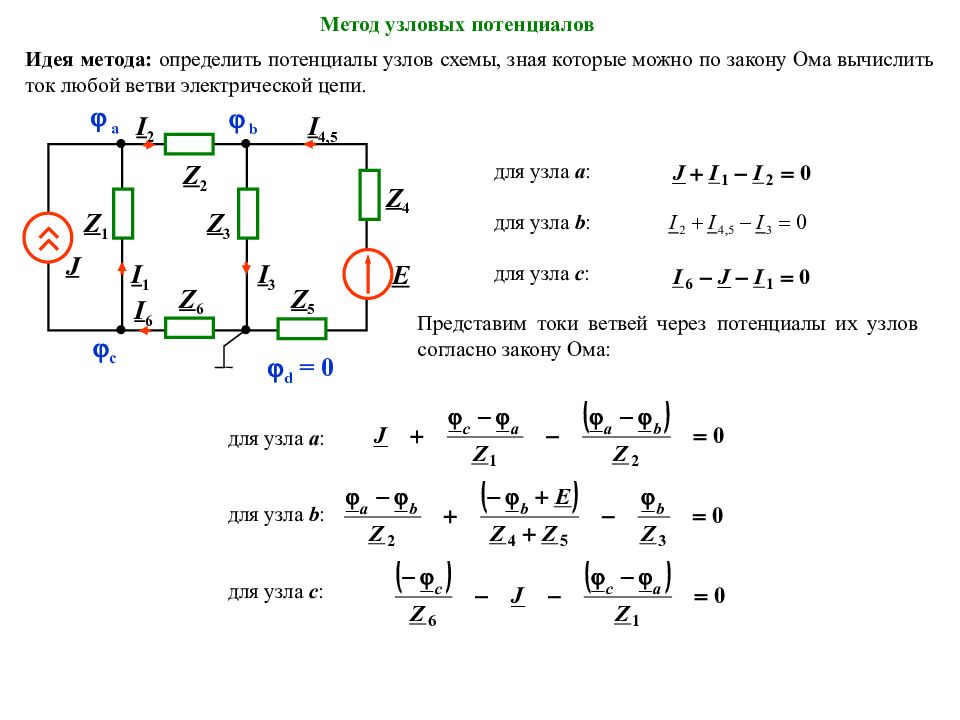
Метод узловых потенциалов Идея метода: определить потенциалы узлов схемы, зная которые можно по закону Ома вычислить ток любой ветви электрической цепи. для узла а : для узла b : для узла с : Представим токи ветвей через потенциалы их узлов согласно закону Ома: для узла а : для узла b : для узла с : a I 1 I 3 b с I 2 Z 3 J Z 1 Z 2 I 4,5 I 6 Z 6 Z 4 E Z 5 d = 0
Слайд 124
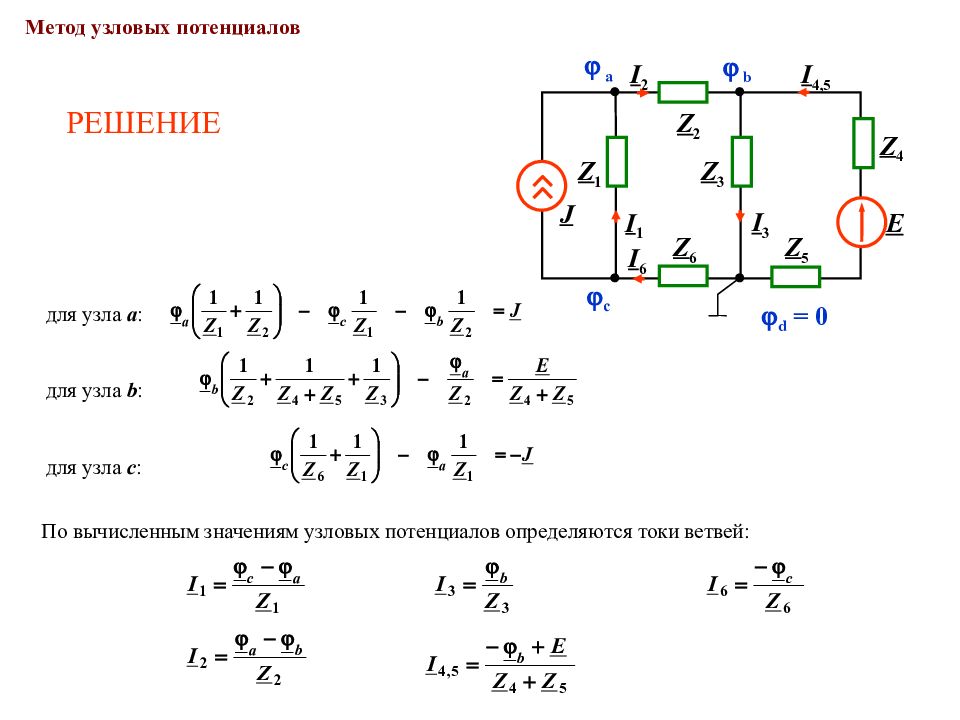
Метод узловых потенциалов РЕШЕНИЕ для узла а : для узла b : для узла с : По вычисленным значениям узловых потенциалов определяются токи ветвей: a I 1 I 3 b с I 2 Z 3 J Z 1 Z 2 I 4,5 I 6 Z 6 Z 4 E Z 5 d = 0
Слайд 125
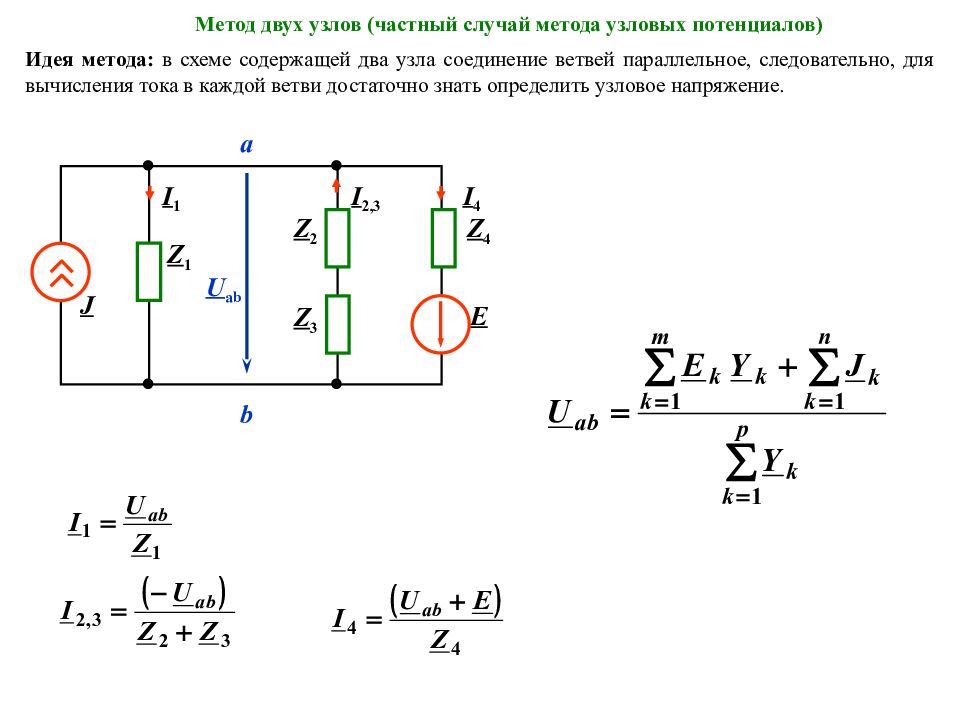
Метод двух узлов (частный случай метода узловых потенциалов) Идея метода: в схеме содержащей два узла соединение ветвей параллельное, следовательно, для вычисления тока в каждой ветви достаточно знать определить узловое напряжение. I 1 b Z 3 J Z 1 I 2,3 I 4 U ab Z 4 E Z 2 а
Слайд 126
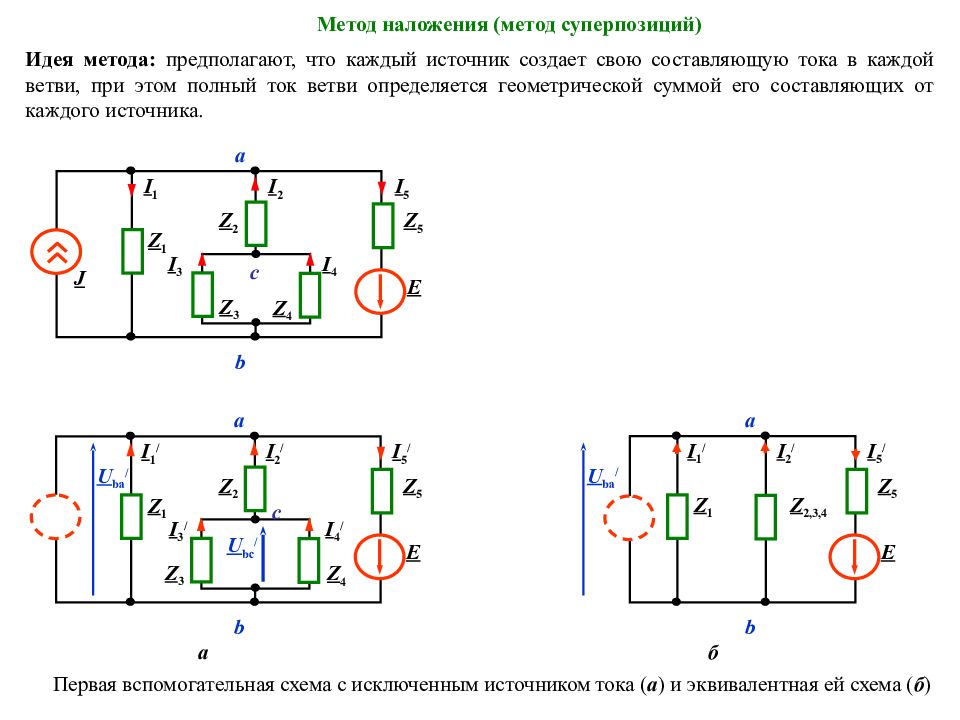
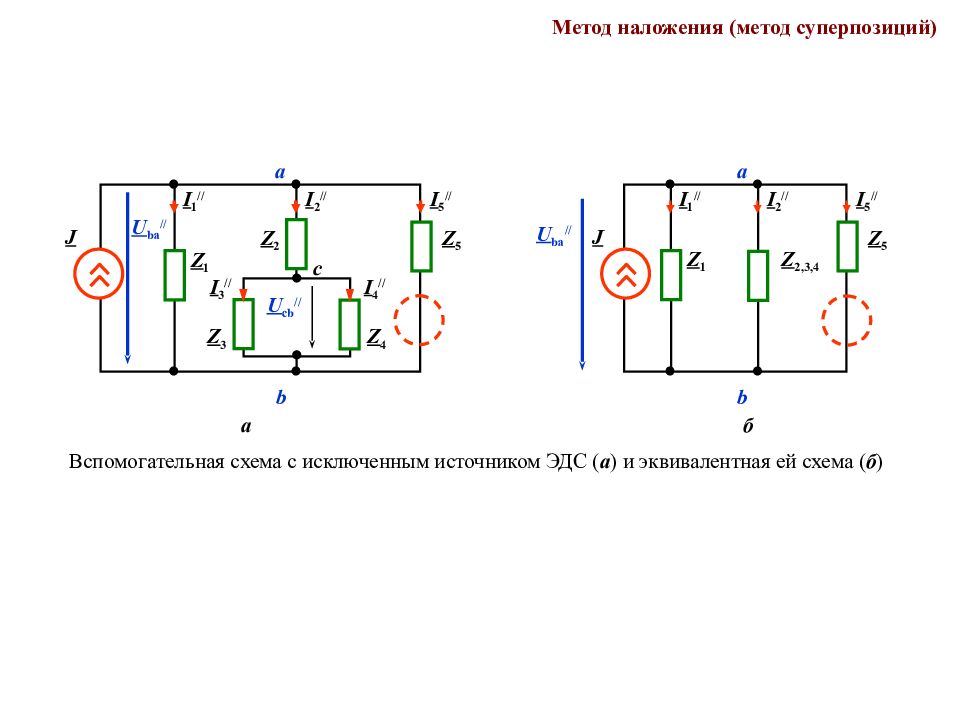
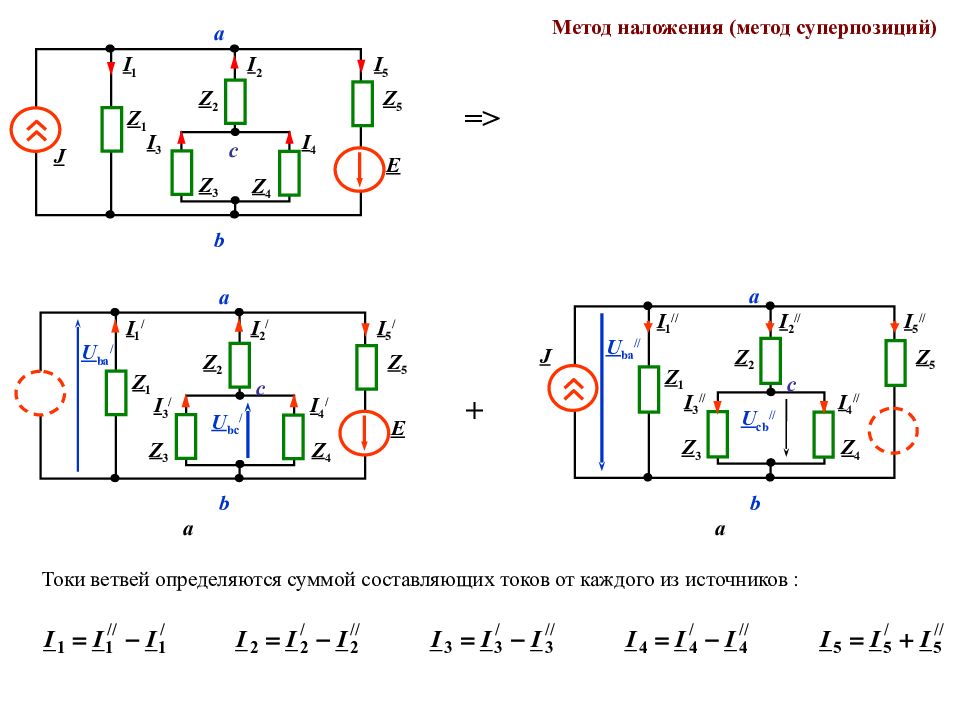
Метод наложения (метод суперпозиций) Идея метода: предполагают, что каждый источник создает свою составляющую тока в каждой ветви, при этом полный ток ветви определяется геометрической суммой его составляющих от каждого источника. b I 1 Z 3 J Z 1 I 2 I 5 Z 5 E Z 2 Z 4 I 3 с а I 4 Первая вспомогательная схема с исключенным источником тока ( а ) и эквивалентная ей схема ( б ) U bc / I 2 / b I 1 / Z 3 Z 1 I 5 / Z 5 E Z 2 Z 4 I 3 / с а I 4 / а U ba / б I 2 / b I 1 / Z 1 I 5 / Z 5 E Z 2,3,4 а U ba /
Слайд 127
Метод наложения (метод суперпозиций) Вспомогательная схема с исключенным источником ЭДС ( а ) и эквивалентная ей схема ( б ) U cb // I 2 // b I 1 // Z 3 Z 1 I 5 // Z 5 Z 2 Z 4 I 3 // с I 4 // а U ba // J а I 2 // b I 1 // Z 1 I 5 // Z 5 Z 2,3,4 б J U ba // а
Слайд 128
Метод наложения (метод суперпозиций) U bc / I 2 / b I 1 / Z 3 Z 1 I 5 / Z 5 E Z 2 Z 4 I 3 / с а I 4 / а U ba / U cb // I 2 // b I 1 // Z 3 Z 1 I 5 // Z 5 Z 2 Z 4 I 3 // с I 4 // а U ba // J а = > + Токи ветвей определяются суммой составляющих токов от каждого из источников : b I 1 Z 3 J Z 1 I 2 I 5 Z 5 E Z 2 Z 4 I 3 с а I 4
Слайд 129
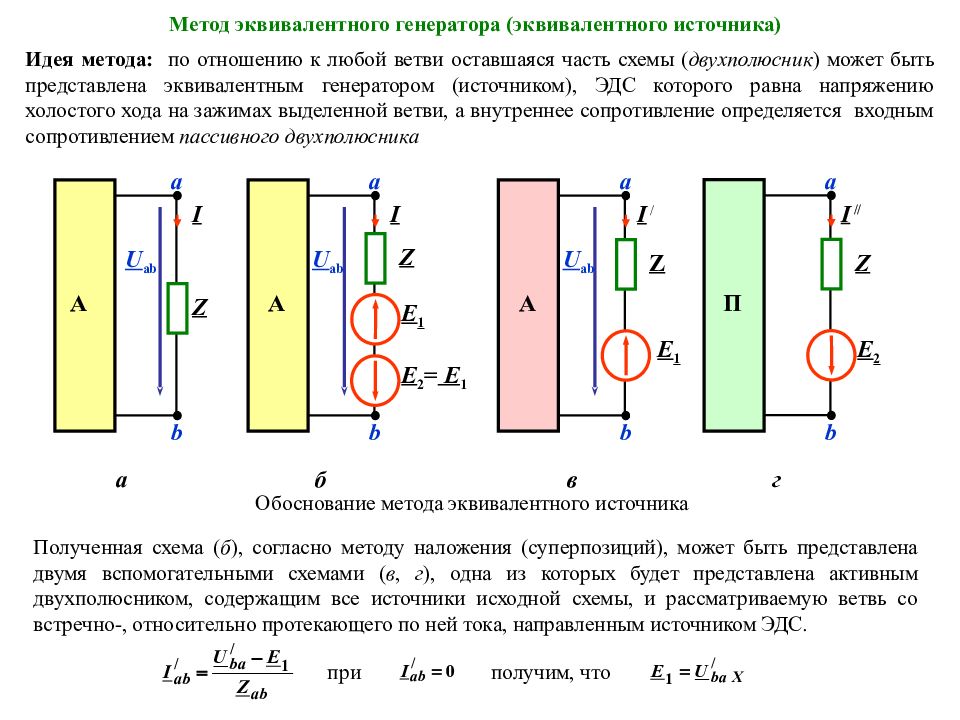
Метод эквивалентного генератора (эквивалентного источника) Идея метода: по отношению к любой ветви оставшаяся часть схемы ( двухполюсник ) может быть представлена эквивалентным генератором (источником), ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление определяется входным сопротивлением пассивного двухполюсник а Обоснование метода эквивалентного источника b I Z А а а U ab E 2 = E 1 b I Z А а б E 1 U ab b I / Z А а в E 1 U ab b I // Z П а г E 2 Полученная схема ( б ), согласно методу наложения (суперпозиций), может быть представлена двумя вспомогательными схемами ( в, г ), одна из которых будет представлена активным двухполюсником, содержащим все источники исходной схемы, и рассматриваемую ветвь со встречно-, относительно протекающего по ней тока, направленным источником ЭДС. при получим, что
Слайд 130
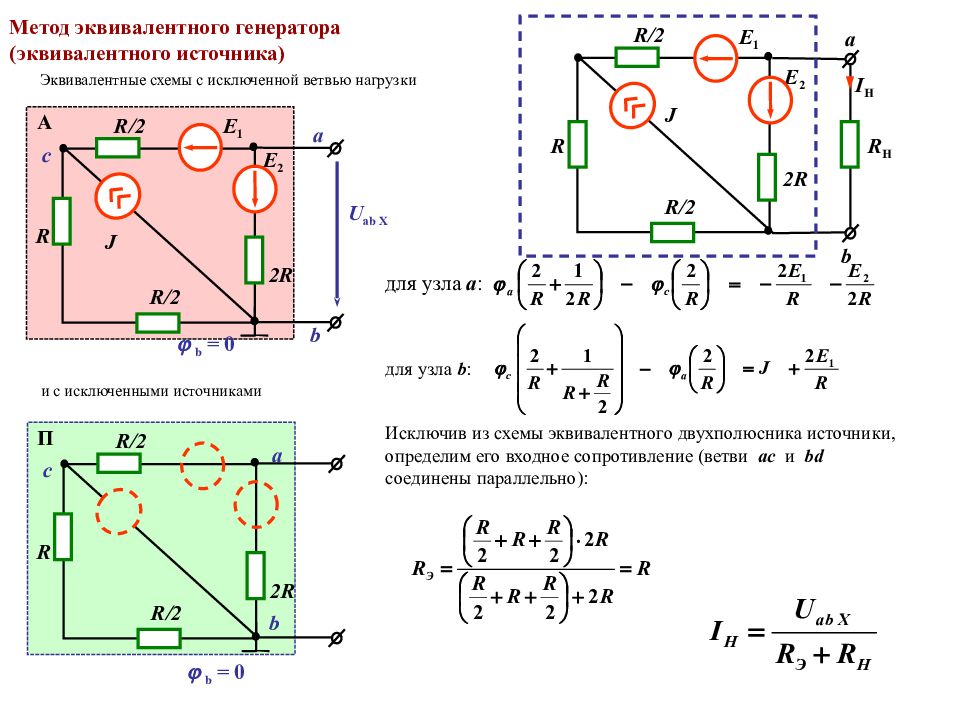
Метод эквивалентного генератора (эквивалентного источника) Эквивалентные схемы с исключенной ветвью нагрузки b 2 R E 1 R /2 а R /2 R J А с E 2 U ab X b = 0 b 2 R R /2 а R /2 R П с b = 0 для узла а : для узла b : Исключив из схемы эквивалентного двухполюсника источники, определим его входное сопротивление (ветви ас и bd соединены параллельно): b I H 2R R /2 а R /2 R J R H E 1 E 2 и с исключенными источниками
Слайд 131
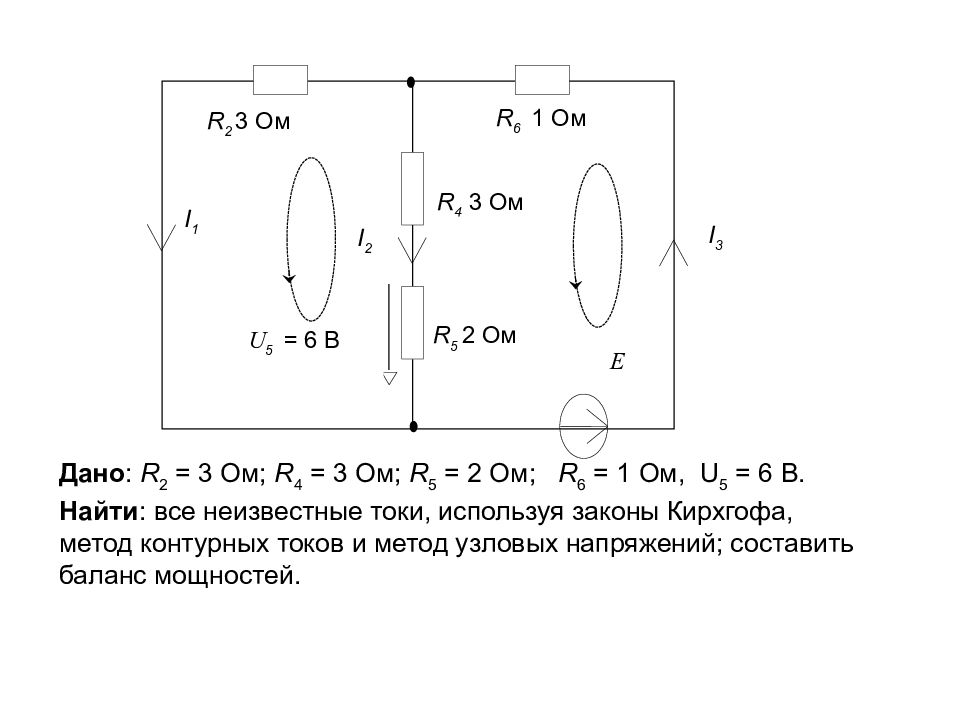
I 1 I 2 R 5 2 Ом I 3 R 2 3 Ом R 4 3 Ом R 6 1 Ом E U 5 = 6 В Дано : R 2 = 3 Ом; R 4 = 3 Ом; R 5 = 2 Ом; R 6 = 1 Ом, U 5 = 6 В. Найти : все неизвестные токи, используя законы Кирхгофа, метод контурных токов и метод узловых напряжений; составить баланс мощностей.
Слайд 132
Расчет по законам Кирхгофа. 1) определяем топологию цепи общее количество ветвей р * = 3 количество ветвей с источниками тока р ит = 0 количество ветвей с неизвестными токами р = ( р * – р ит ) = 3 – 0 = 3 количество узлов q = 2 количество независимых контуров n = p – ( q – 1) = 3 – (2 – 1) = 2 2) составляем ( q – 1) узловых уравнений по первому закону Кирхгофа узел 1: I 1 + I 2 - I 3 = 0 3) составляем n контурных уравнений по второму закону Кирхгофа контур I: R 2 · I 1 + ( R 4 ·+ R 5 )· I 2 = Е контур II: R 6 · I 3 – ( R 4 + R 5 )· I 2 = 0, или 9,6 - ( R 4 + R 5 )· I 2 = 0 4) объединяем узловые и контурные уравнения в системе
Слайд 134
I 1 I 2 R 5 2 Ом I 3 R 2 3 Ом R 4 3 Ом R 6 1 Ом E U 5 = 6 В I 22 I 11 Расчет методом контурных токов определяем собственные и общие сопротивления R 11 = R 2 + R 4 + R 5 = 3 + 3 + 2 = 8 Ом R 22 = R 2 + R 6 = 3 + 1 = 4 Ом R 12 = R 12 = R 2 = 3 Ом 2) определяем контурные ЭДС Е 11 = 0 Е 22 = Е В 3) составляем систему уравнений Подставляем значения и, учитывая, что , решаем полученную систему , 4) определяем неизвестные токи I 1 = I 22 – I 11 = 8 – 3 = 5 А I 2 = I 11 = 3 А I 3 = I 22 = 8 А
Слайд 135
Расчет методом узловых напряжений 1) определяем собственные и общие проводимости 2) определяем токи, обусловленные источниками энергии в цепи 3) составляем систему уравнений Учитывая, что , определим Ток I 1 определим по закону Ома Ток I 3 определим по первому закону Кирхгофа Величину определим из формулы См g 11 =