Автор: к.ф.-м.н., доцент Черкасова О.А. ФИЗИКА Лекция 10
Автор: к.ф.-м.н., доцент Черкасова О.А. 2 Физическая система : У фермионов нет принципа неразличимости как у классических элементов статистической системы. Они различаются квантовыми числами. Имеем термодинамическую систему из N невзаимодействующих частиц. Энергия частицы в i -том состоянии ε i. Система находится в равновесном состоянии T = Const. Классическая постановка : Какова вероятность, что в состоянии ε i находится N i частиц? Квантовая интерпретация: Какова вероятность, что на данном энергетическом уровне ε i находится один электрон и это состояние реализуется α способами (другие квантовые числа)?
Автор: к.ф.-м.н., доцент Черкасова О.А. 3 Физическая система : При Т ≠ 0 число N i может изменяться (переход на более низкие энергетические уровни без получения энергии из вне), т.е. имеем ТД систему, состоящую из нескольких подсистем с изменяющимся числом частиц. Для описания - распределение Гиббса. Равновесное состояние достигается при равенстве температур и химических потенциалов. Из термрдинамики : В ТДС, в которых происходит не только обмен тепловой энергий, но происходит изменение количество вещества первое начало примет вид: δ Q – количество тепла, сообщённое системе, µ - химический потенциал, δА – работа, совершённая над системой внешними силами, µ dN – количество вещества.
Автор: к.ф.-м.н., доцент Черкасова О.А. 4 Физическая система : Гамильтониан для таких систем имеет вид: Гамильтониан для подсистемы Каноническое (классическое) распределение Гиббса Применим полученное распределение к фермионам, т.е для любого уровня ε i имеем лишь два значения N i : 0 или 1 ( уровень свободен - или занят) и используя условие нормировки:
Автор: к.ф.-м.н., доцент Черкасова О.А. 5 Физическая система : Распределение Ферми-Дирака для электронов по энергиям в квантовой системе: Анализ полученного результата: В квантовой физике принято называть химический потенциал уровнем Ферми. Найдём его физический смысл. Пусть Т=0К. Тогда Все уровни меньше уровня Ферми заняты. При Т=Т 1 > 0К, Уровни Ферми уровни свободны. Распределение энергетических уровней, занятых электронами
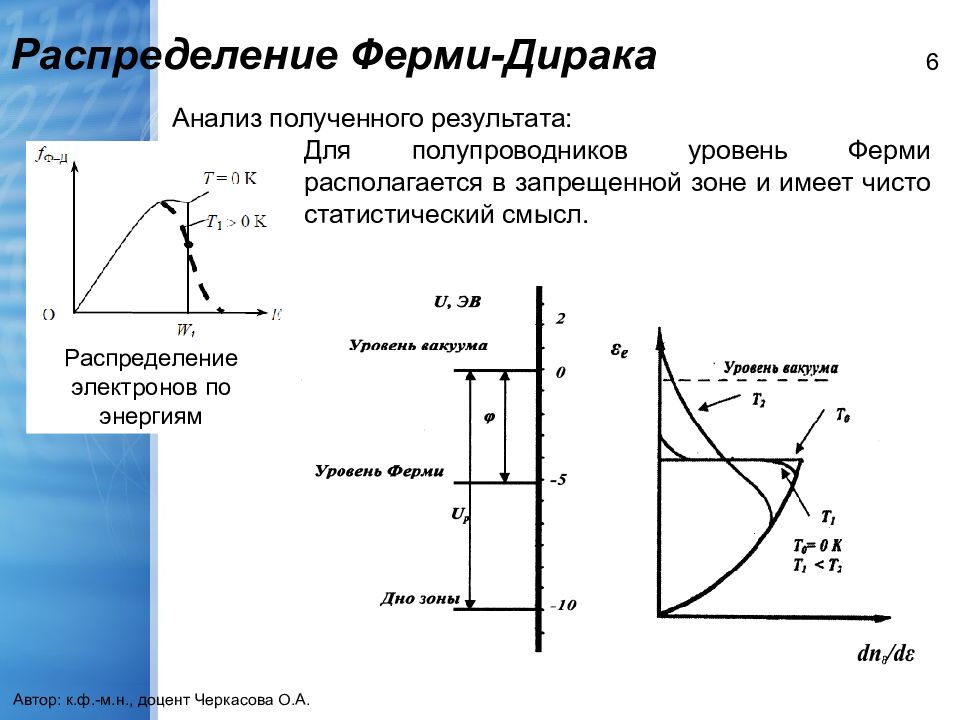
Автор: к.ф.-м.н., доцент Черкасова О.А. 6 Анализ полученного результата: Для полупроводников уровень Ферми располагается в запрещенной зоне и имеет чисто статистический смысл. Распределение электронов по энергиям
Автор: к.ф.-м.н., доцент Черкасова О.А. 7 Анализ полученного результата: При T=0 все N электронов стремятся занять состояния с самыми малыми значениями энергии, соблюдая принцип Паули. В таком случае в k-пространстве занятые состояния окажутся внутри шара радиуса r F. Поверхность этого шара называется поверхностью Ферми, а отвечающая ей энергия электронов - энергией Ферми. Энергия Ферми зависит от концентрации свободных электронов n и вычисляется по формуле: границы первой зоны Бриллюэна
Автор: к.ф.-м.н., доцент Черкасова О.А. 8 Анализ полученного результата: Равновесие в ТДС с обменом элементами наступает при равенстве температур и химических потенциалов. Тогда уровень Ферми определяет равновесное состояние электронов (фермионов) в кристаллах. Распределение Ф-Д позволяет найти относительное число электронов в единице объёма с энергиями в заданном интервале: При распределение переходит в классическое распределение частиц по энергиям типа распределения Максвелла
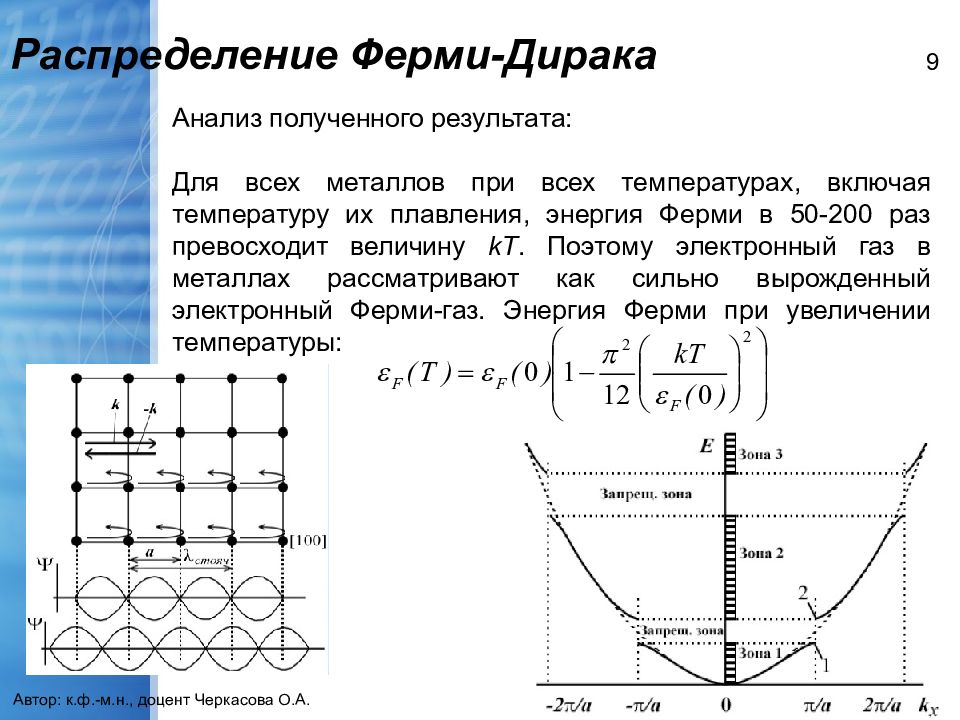
Автор: к.ф.-м.н., доцент Черкасова О.А. 9 Анализ полученного результата: Для всех металлов при всех температурах, включая температуру их плавления, энергия Ферми в 50-200 раз превосходит величину kT. Поэтому электронный газ в металлах рассматривают как сильно вырожденный электронный Ферми-газ. Энергия Ферми при увеличении температуры:
Автор: к.ф.-м.н., доцент Черкасова О.А. 10 Анализ полученного результата: У валентных электронов появляется характеристика связанная с периодическим полем кристалла – эффективная масса электронов: При малых значениях k, ее значение положительное, а при k близких к границе зоны Бриллюэна - отрицательным. В последнем случае получается, что внешняя сила не ускоряет, а тормозит электрон. Это связано с влиянием периодического поля кристалла на движение электрона. Такие электроны ведут себя во внешних электромагнитных полях как частицы с отрицательной массой или как положительно заряженные частицы.
Автор: к.ф.-м.н., доцент Черкасова О.А. 11 Если электрон имеет энергию E < ε F, то, входя в металл, он понижает его температуру (т. е. охлаждает ), а выходя из металла, повышает его температуру (т. е. нагревает ). Если же энергия электрона Е > ε F, то, входя в металл, он его нагревает, а выходя из металла, охлаждает. ФМ: а) Внутри вещества энергия отрицательна, на поверхности = 0, вне кристалла –положительна; б) Распределение потенциальной энергии вблизи поверхности кристалла претерпевает «скачок»: Под работой выхода следует понимать ту энергию, которую необходимо передать электрону, находящемуся на уровне Ферми, чтобы удалить его из металла в вакуум :
Автор: к.ф.-м.н., доцент Черкасова О.А. 12 Причины возникновения работы выхода: Если при тепловом движении электрон вылетит из металла, то он наводит (индуцирует) на его поверхности положительные заряды, равные по величине заряду электрона. В результате этого возникает сила притяжения между электроном и поверхностью металла, называемая силой «электрического изображения », которая стремится вернуть электрон обратно в металл. Образование двойного электрического слоя, возникающего за счет того, что электроны, совершая тепловое движение, могут пересекать поверхность металла и удаляться от нее на небольшие расстояния (порядка атомных). В результате двойной электрический слой, действующий подобно конденсатору, не создает электрического поля во внешнем пространстве.
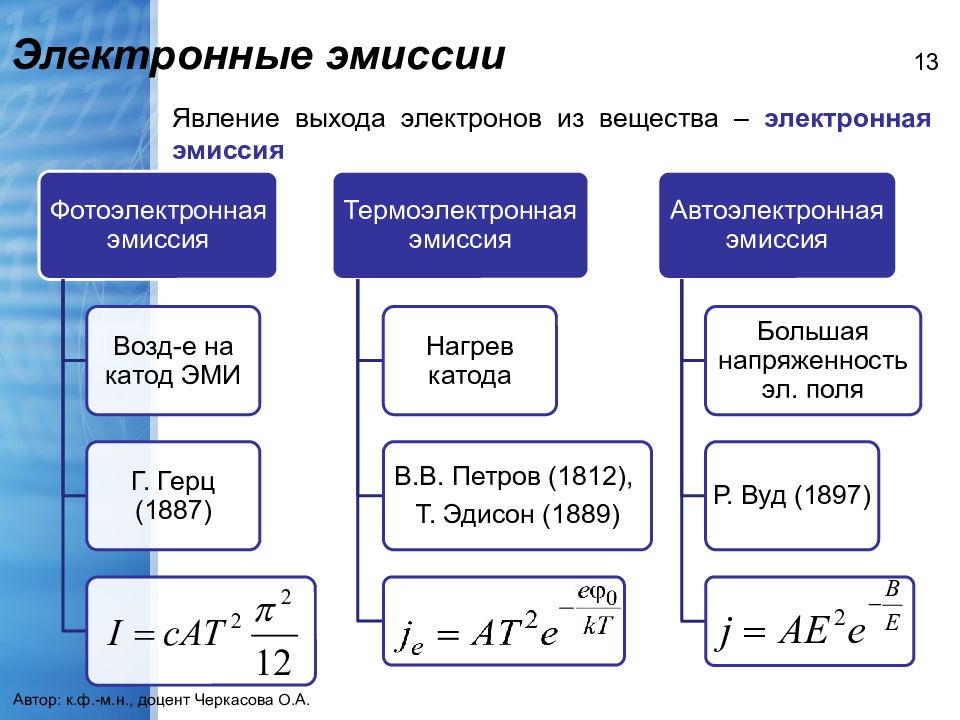
Автор: к.ф.-м.н., доцент Черкасова О.А. 13 Явление выхода электронов из вещества – электронная эмиссия
Автор: к.ф.-м.н., доцент Черкасова О.А. 14
Автор: к.ф.-м.н., доцент Черкасова О.А. 15 При контакте двух разных металлов между ними возникает разность потенциалов, которую называют контактной разностью потенциалов. Явление открыто в 1797 г. итальянским ученым Алессандро Вольта, который установил два закона: При контакте двух разных металлов между ними возникает разность потенциалов, зависящая от их химического состава и температуры; Разность потенциалов между концами разомкнутой цепи, составленной из нескольких, последовательно соединенных металлических проводников, которые находятся при одинаковой температуре, не зависит от промежуточных проводников и полностью определяется контактной разностью потенциалов крайних проводников.
Автор: к.ф.-м.н., доцент Черкасова О.А. 16 Пример: Металл-маталл с разными уровнями Ферми Возникает разность потенциалов между любыми двумя точками, которые находятся в непосредственной близости от поверхности проводников, однако вне их. Такая разность называется внешней контактной разностью потенциалов : В силу эквипотенциальности поверхностей разность не зависит от положения точек a и b. 2. Начинается диффузия электронов из одного металла в другой. Так как диффундирующий поток из металла 1 в металл 2 будет больше, то металл 1 зарядится положительно, а металл 2 – отрицательно. Между металлами возникает разность потенциалов, которая называется внутренней контактной разностью потенциалов :
Автор: к.ф.-м.н., доцент Черкасова О.А. 17 Пример: Металл-маталл с разными уровнями Ферми
Автор: к.ф.-м.н., доцент Черкасова О.А. 18 Термоэлектрическими явлениями называют явления, в которых проявляется связь между электрической и молекулярно-тепловой формами движения материи.
Автор: к.ф.-м.н., доцент Черкасова О.А. 19 Расчеты электропроводимости металлов приводят к выражению для удельной электрической проводимости металла n – концентрация электронов проводимости в металле; l F – средняя длина свободного пробега электрона, имеющего энергию Ферми; υ F – средняя скорость теплового движения такого электрона объясняет зависимость удельной проводимости от температуры, а также аномально большие величины средней длины свободного пробега электронов в металле.
Автор: к.ф.-м.н., доцент Черкасова О.А. 20 Рассеяние «электронных волн» на неоднородностях является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами. Свойства сверхпроводимости ( Камерлинг-Оннес ) 1. В отсутствии магнитного поля переход в сверхпроводящее состояние сопровождается скачкообразным изменением теплоемкости, а при переходе в сверхпроводящее состояние во внешнем магнитном поле скачком изменяются и теплопроводность и теплоемкость. 2. Достаточно сильное магнитное поле и сильный электрический ток, протекающий по сверхпроводнику, разрушают сверхпроводящее состояние. 3. В сверхпроводящем состоянии магнитное поле в толще сверхпроводника отсутствует.
Автор: к.ф.-м.н., доцент Черкасова О.А. 21 Эффект Мейсснера - при охлаждении сверхпроводника ниже критической температуры магнитное поле из него вытесняется.
Автор: к.ф.-м.н., доцент Черкасова О.А. 22 Качественное объяснение явления сверхпроводимости: Между электронами металла помимо кулоновского отталкивания, в достаточной степени ослабляемого экранирующем действием положительных ионов решетки, в результате электрон-фононного взаимодействия возникает слабое взаимное притяжение. Это взаимное притяжение при определенных условиях может преобладать над отталкиванием. Связанное состояние, которое образуется между электронами вследствие их притяжения, называется куперовской парой. P - вектора поляризации, M – вектора намагниченности, j вн - внешний или сторонний ток, не включенный в ток поляризации и намагниченности.
Автор: к.ф.-м.н., доцент Черкасова О.А. 23 Электроны, входящие в куперовскую пару, имеют противоположно направленные спины. Поэтому спин такой пары равен нулю, и она представляет собой бозон. К бозе-частицам принцип Паули неприменим, т.к. при сверхнизких температурах они скапливаются в основном состоянии, из которого их довольно трудно перевести в возбужденное состояние. Система куперовских пар может под действием внешнего электрического поля двигаться без сопротивления со стороны проводника, что и приводит к сверхпроводимости. Эффект Джозефсона (предсказан в 1962 г., обнаружен в 1963 г., Нобелевская премия 1973 г.) – протекание сверхпроводящего тока сквозь тонкий слой диэлектрика (≈ 1 нм), разделяющий два сверхпроводника. Эффект Джозефсона используется для измерения слабых магнитных полей (~10 -18 Тл), токов (~10 -10 А), и напряжений (10 -15 В), для создания быстродействующих элементов логических устройств ЭВМ.
Автор: к.ф.-м.н., доцент Черкасова О.А. 24 При достаточно малой толщине изолятора (<10 –7 см) возможно туннелирование куперовских пар через переход. А – матричные элементы энергии системы, характеризует вероятность туннелирования электронов, φ – фазы контактов, ρ – плотность электронов. Если U=U 0 =const, то Если U=0, то I≠0 → стационарный эффект Джозефсона.
