Первый слайд презентации: Формализованные методы макроэкономического прогнозирования. Прогнозирование временных рядов
Дисциплина «Макроэкономическое планирование и прогнозирование ». Часть 3
Слайд 2: Вопросы темы:
Компонентный состав временных рядов. Методы выравнивания рядов динамики. Сглаживание временных рядов методом простых скользящих средних. Особенности применения взвешенных скользящих средних. Метод аналитического выравнивания.
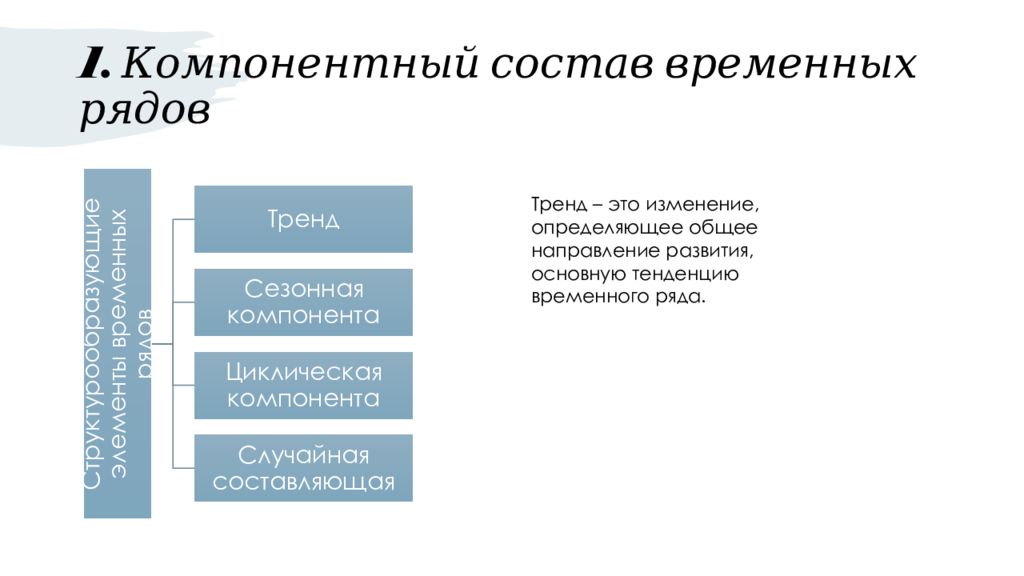
Слайд 3: 1. Компонентный состав временных рядов
Тренд – это изменение, определяющее общее направление развития, основную тенденцию временного ряда.
Слайд 4
Наряду с долговременными тенденциями, могут быть регулярные колебания. Если период колебаний составляет менее 1 года, такие колебания называются сезонными. Они вызываются природно-климатическими условиями (например, колебания цен на овощи и фрукты) или социальными причинами (увеличение покупок в предпраздничный период). Если период колебаний больше 1 года, считается, что во временных рядах имеет место циклическая составляющая. Это могут быть циклы деловой активности, демографические, инвестиционные и другие циклы.
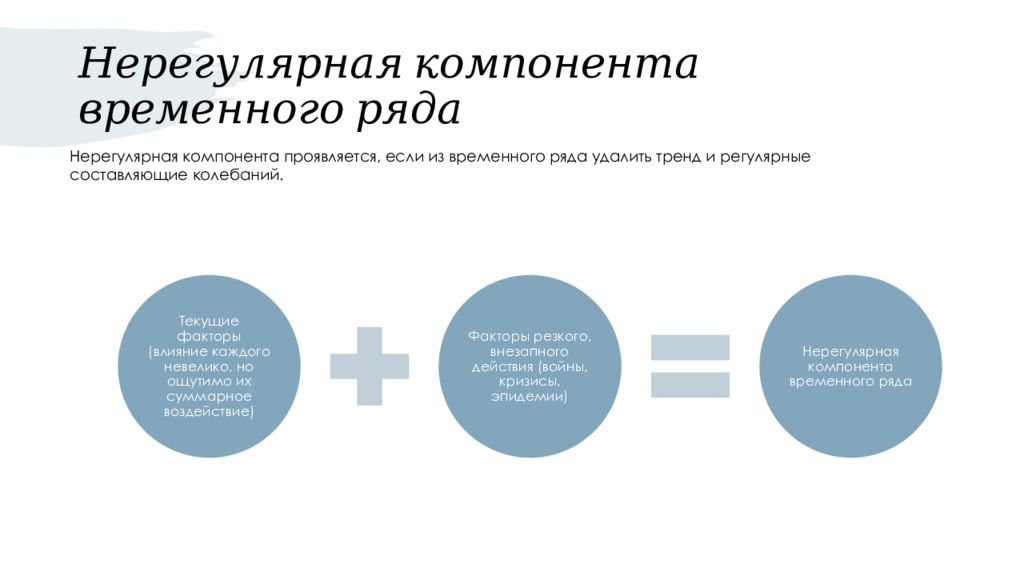
Слайд 5: Нерегулярная компонента временного ряда
Нерегулярная компонента проявляется, если из временного ряда удалить тренд и регулярные составляющие колебаний.
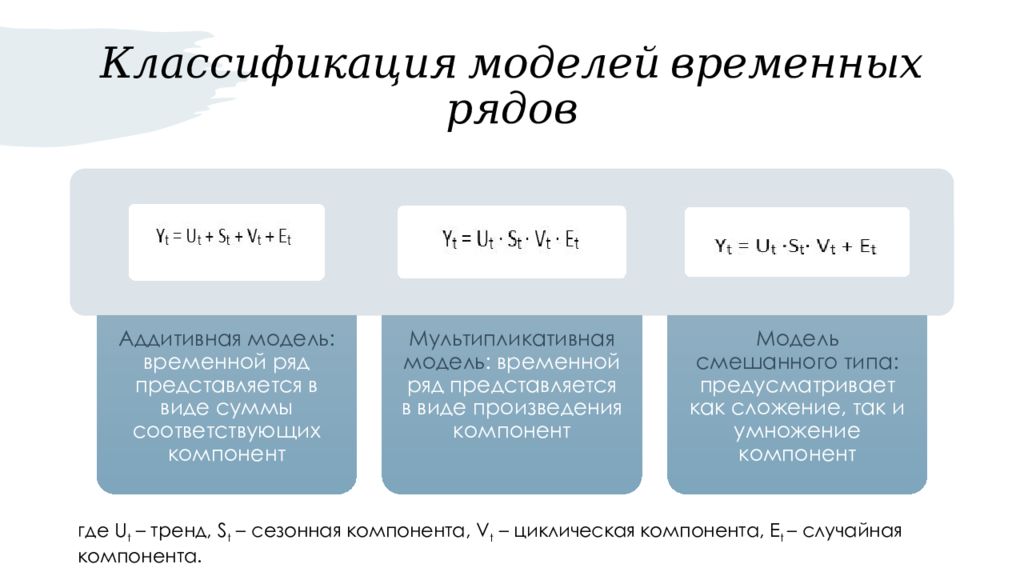
Слайд 6: Классификация моделей временных рядов
где U t – тренд, S t – сезонная компонента, V t – циклическая компонента, E t – случайная компонента.
Важной задачей, возникающей при анализе рядов динамики, является определение основной тенденции в развитии исследуемого процесса. Распространенным приёмом, применяемым для выявления тенденции развития, выступает выравнивание (сглаживание) временного ряда. Сущность этого приёма состоит в том, что производится замена фактических уровней временного ряда расчетными уровнями, которые оказываются менее подверженными колебаниям, и это способствует более четкому проявлению тенденции развития.
Слайд 10: 3. Сглаживание временных рядов с помощью простых скользящих средних
Метод скользящих средних – это метод выравнивания временного ряда, основанный на вычислении средних величин за укрупненные период времени. Этот метод позволяет сгладить как случайные, так и периодические колебания и выявить тенденцию в развитии процесса. Цель метода – абстрагироваться от влияния случайных факторов, взаимопогасить их влияние в отдельные годы. Метод опирается на теорему Вейерштрасса, гласящую, что «любая гладкая функция при самых общих допущениях может быть локально (то есть в ограниченном интервале изменения её аргумента t) представлена алгебраическим полиномом подходящей степени».
Слайд 13: Расчет скользящей средней
На первом этапе необходимо установить длину интервала сглаживания L. Удобнее всего брать длину интервала в виде нечетного числа: L = 2P+1, где Р – целое положительное число, 2Р+1 – число уровней активного участка сглаживания, из них Р-уровней предшествуют центральному уровню, и Р-уровней следуют за центральным уровнем активного участка. В этом случае значение скользящей средней будет приходиться на средний член интервала. Наблюдения, которые берутся для расчета среднего значения, называются активным участком сглаживания. Если L – нечетное число, то все уровни активного участка сглаживания можно представить так: p p Y t-p, Y t-p+1,…, Y t-1,Y t,Y t+1,…,Y t+p-1,Y t+p t-p t t+p
Слайд 14: Скользящая средняя определяется по формуле:
Где Y i – фактическое значение i - того уровня, – значение скользящей средней в момент времени t, 2р+1 – длина интервала сглаживания.
Слайд 15: Расчет простой скользящей средней, если L – четное число
Таким образом, количество уровней, рассматриваемое на каждом активном участке, равно 2p+1, при этом первое и последнее наблюдение на активном участке принято брать с половинными весами.
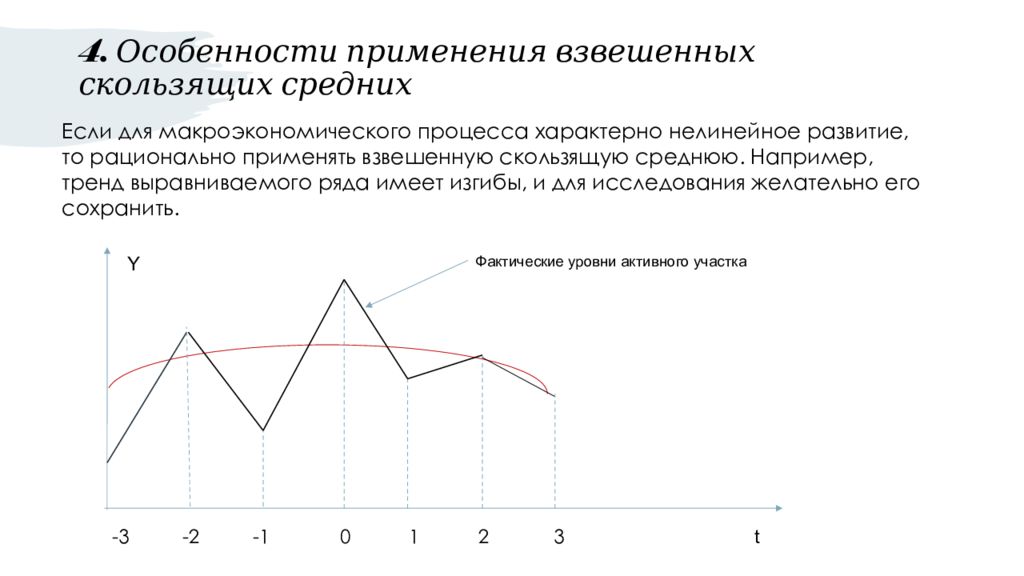
Слайд 16: 4. Особенности применения взвешенных скользящих средних
Если для макроэкономического процесса характерно нелинейное развитие, то рационально применять взвешенную скользящую среднюю. Например, тренд выравниваемого ряда имеет изгибы, и для исследования желательно его сохранить. Y t -3 -2 -1 0 1 2 3 Фактические уровни активного участка
Слайд 17: Расчет взвешенной скользящей средней
При построении взвешенной скользящей средней на каждом участке значение центрального уровня заменяется на расчетное, определяемое по средней арифметической взвешенной: где f i – весовые коэффициенты. Таким образом, простая скользящая средняя – частный случай взвешенной скользящей средней.
Слайд 18: Весовые коэффициенты для расчета взвешенной скользящей средней
L Весовые коэффициенты 5 7 9 L Весовые коэффициенты 5 7 9 Например, пятичленная взвешенная скользящая средняя будет определяться так:
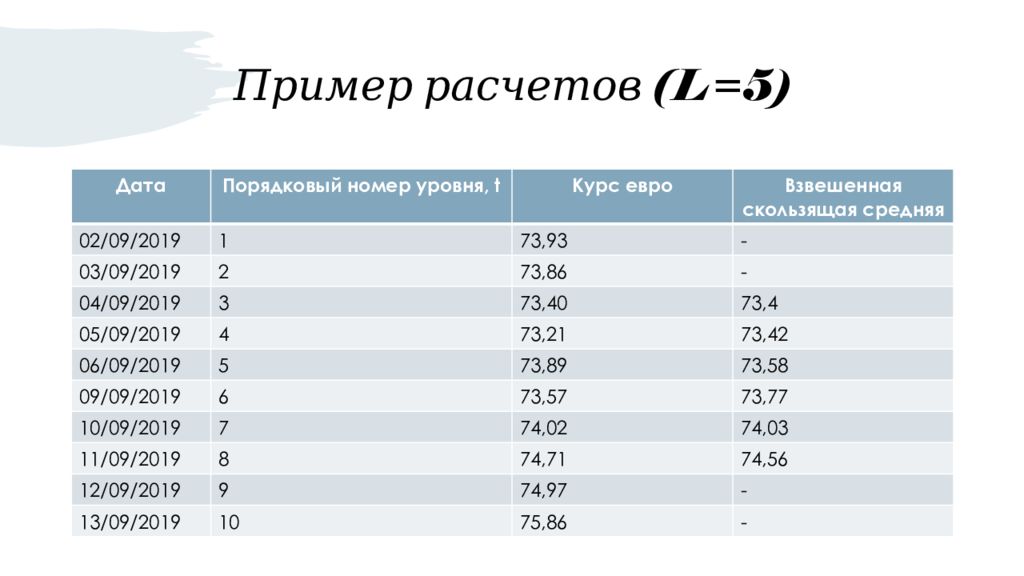
Слайд 19: Пример расчетов (L=5)
Дата Порядковый номер уровня, t Курс евро Взвешенная скользящая средняя 02/09/2019 1 73,93 - 03/09/2019 2 73,86 - 04/09/2019 3 73,40 73,4 05/09/2019 4 73,21 73,42 06/09/2019 5 73,89 73,58 09/09/2019 6 73,57 73,77 10/09/2019 7 74,02 74,03 11/09/2019 8 74,71 74,56 12/09/2019 9 74,97 - 13/09/2019 10 75,86 -
Показательная функция выпуска имеет вид: Параметр а характеризует начальные условия, параметр b – постоянный темп роста Если b>1, то по мере роста t кривая загибается вверх. Если b<1, то кривая Y имеет отрицательный наклон. Прологарифмируем выражение для Y t. Получим: Пусть lna =A, lnb =B Для оценивания неизвестных параметров a и b необходимо решить систему уравнений:
Слайд 21: 5. Метод аналитического выравнивания
Данный метод основан на вычислении значений выравненного ряда по соответствующим математическим формулам. Для определения линии тренда обычно используются полиномы первой или второй степени. Полином первой степени на графике изображается прямой линией и используется для описания процессов, развивающихся во времени равномерно. Полином второй степени: применяется в тех случаях, когда процесс развивается равноускоренно. Для оценивания полиномов первой степени применяется система из двух уравнений (см. предыдущий слайд):
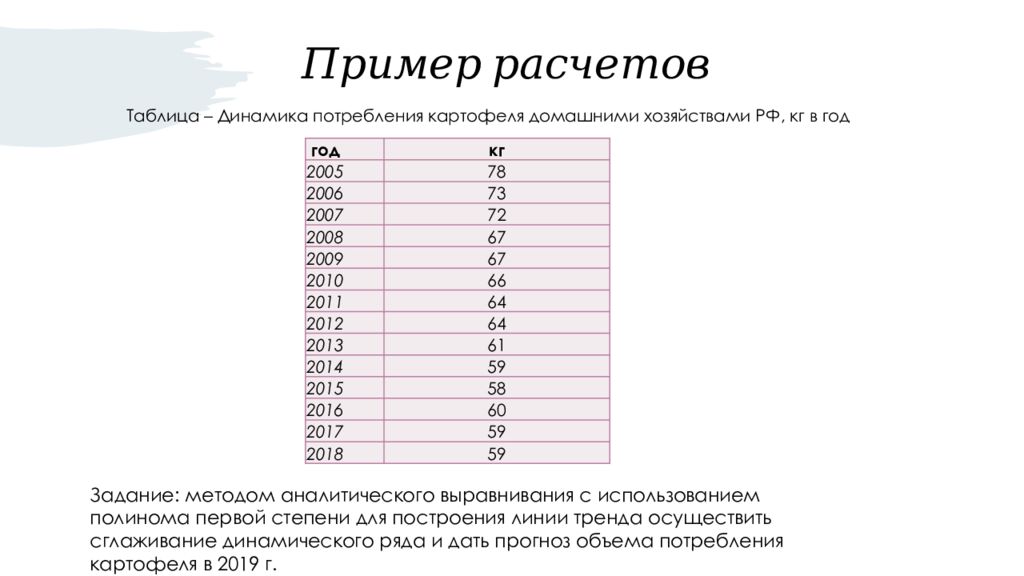
Слайд 22: Пример расчетов
Таблица – Динамика потребления картофеля домашними хозяйствами РФ, кг в год год кг 2005 78 2006 73 2007 72 2008 67 2009 67 2010 66 2011 64 2012 64 2013 61 2014 59 2015 58 2016 60 2017 59 2018 59 Задание: методом аналитического выравнивания с использованием полинома первой степени для построения линии тренда осуществить сглаживание динамического ряда и дать прогноз объема потребления картофеля в 2019 г.
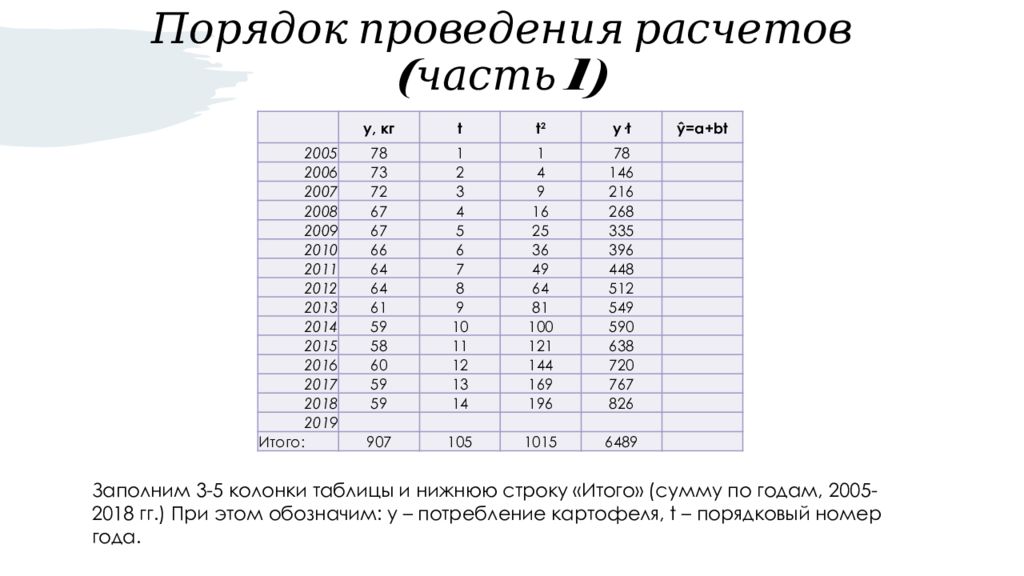
Слайд 23: Порядок проведения расчетов (часть 1)
y, кг t t 2 y·t ŷ=a+bt 2005 78 1 1 78 2006 73 2 4 146 2007 72 3 9 216 2008 67 4 16 268 2009 67 5 25 335 2010 66 6 36 396 2011 64 7 49 448 2012 64 8 64 512 2013 61 9 81 549 2014 59 10 100 590 2015 58 11 121 638 2016 60 12 144 720 2017 59 13 169 767 2018 59 14 196 826 2019 Итого: 907 105 1015 6489 Заполним 3-5 колонки таблицы и нижнюю строку «Итого» (сумму по годам, 2005-2018 гг.) При этом обозначим: y – потребление картофеля, t – порядковый номер года.
Слайд 24: Порядок проведения расчетов (часть 2)
Теперь наша задача состоит в том, чтобы найти значения коэффициентов a и b. Это можно сделать, построив систему уравнений методом аналитического выравнивания (см. слайд № 21):
Слайд 25: Порядок проведения расчетов (часть 3)
a=64,79-7,5b 6489=105 * ( 64,79-7,5b)+ 1015b 6489=6802,95-787,5b+1015b b=313,95/(-227,5)= - 1,38 a=64,79 - (-1,38)*7,5 = 75,14 Обозначим ŷ – выравненное значение объема потребления картофеля, кг: ŷ=75,14-1,38t Теперь можно найти прогнозный объем потребления в 2019 г.: ŷ(2019 )= 75,14-1,38*15=54,44 кг. Данный пример показывает, что при использовании метода аналитического выравнивания с полиномом первой степени прогноз зачастую оказывается неточным, так как исследователь исходит из линейной динамики переменной ( в р ассмотренном примере из нисходящей динамики).
Слайд 26: Рекомендуемая литература
Невская, Н. А. Макроэкономическое планирование и прогнозирование в 2 ч. Часть 1: учебник и практикум для вузов / Н. А. Невская. — 2-е изд., испр. — Москва : Издательство Юрайт, 2020. — 310 с. — (Высшее образование). — Текст : электронный // ЭБС Юрайт [сайт]. — URL: https:// urait.ru/bcode/453446. Гл. 5.
Последний слайд презентации: Формализованные методы макроэкономического прогнозирования. Прогнозирование: Контрольные вопросы:
С какой целью проводится выравнивание временных рядов в макроэкономическом прогнозировании? Приведите примеры макроэкономических показателей, для которых характерна цикличная динамика. Какие факторы обусловливают эту цикличность? В чем состоят достоинства метода простых скользящих средних как метода выравнивания временного ряда? Взвешенных скользящих средних?