РЯДЫ ДИНАМИКИ 1
Виды рядов динамики и задачи, решаемые с их помощью. Базисные и цепные показатели динамики. Средние уровни и показатели динамики. Выявление основной тенденции развития социально-экономических явлений. 2 Вопросы лекции
3 Виды рядов динамики и задачи, решаемые с их помощью.
4 Определение ряда динамики Ряд динамики – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени
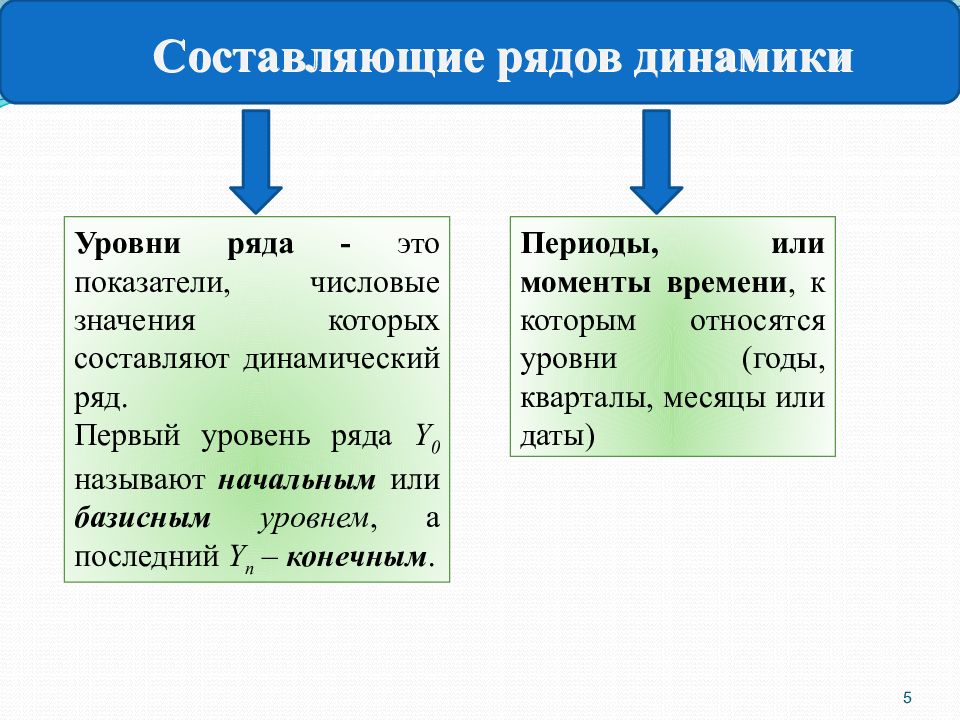
5 Составляющие рядов динамики Уровни ряда - это показатели, числовые значения которых составляют динамический ряд. Первый уровень ряда Y 0 называют начальным или базисным уровнем, а последний Y n – конечным. Периоды, или моменты времени, к которым относятся уровни (годы, кварталы, месяцы или даты)
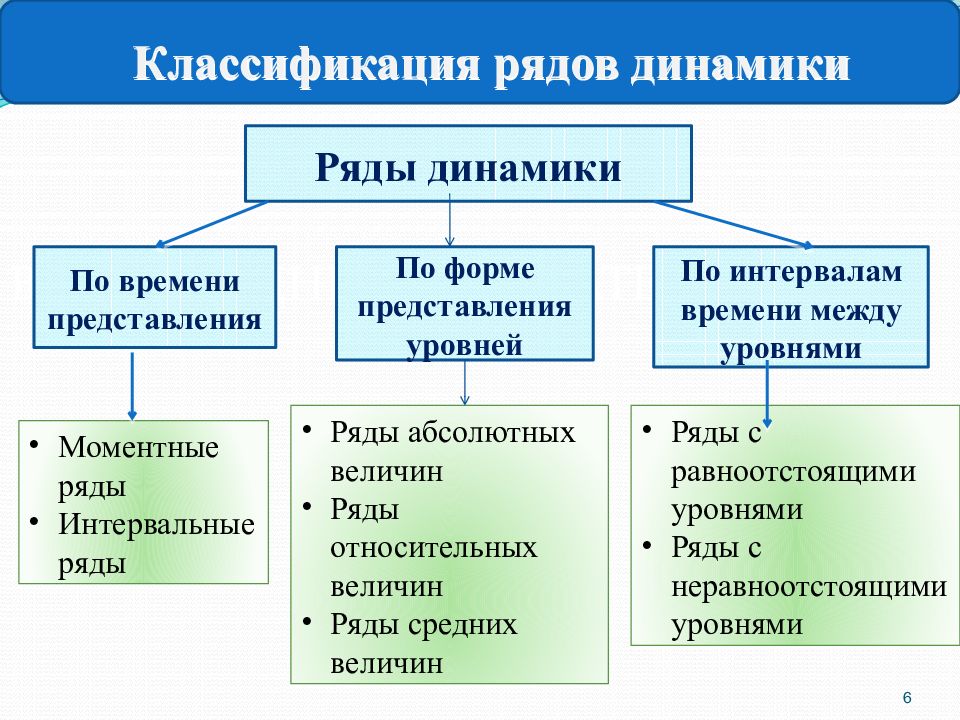
ВЫДЫ СРЕДНИХ ПОКАЗАТЕЛЕЙ Ряды динамики По времени представления По интервалам времени между уровнями Моментные ряды Интервальные ряды Ряды с равноотстоящими уровнями Ряды с неравноотстоящими уровнями 6 Классификация рядов динамики По форме представления уровней Ряды абсолютных величин Ряды относительных величин Ряды средних величин
7 Моментным называется ряд динамики уровни которого характеризуют состояние каких-либо явлений на определенный момент времени, (на начало года, конец года, квартала, месяца.)
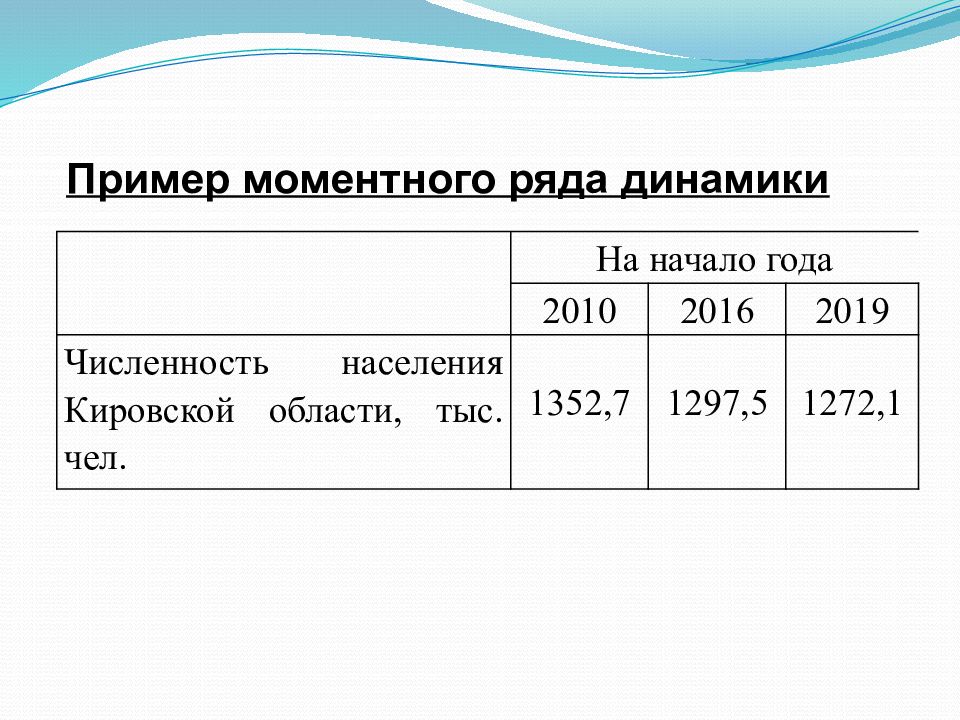
Пример моментного ряда динамики На начало года 2010 2016 2019 Численность населения Кировской области, тыс. чел. 1352,7 1297,5 1272,1
9 Интервальным рядом динамики называется такой ряд, уровни которого характеризуют размеры явлений за определенный промежуток времени. Они отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
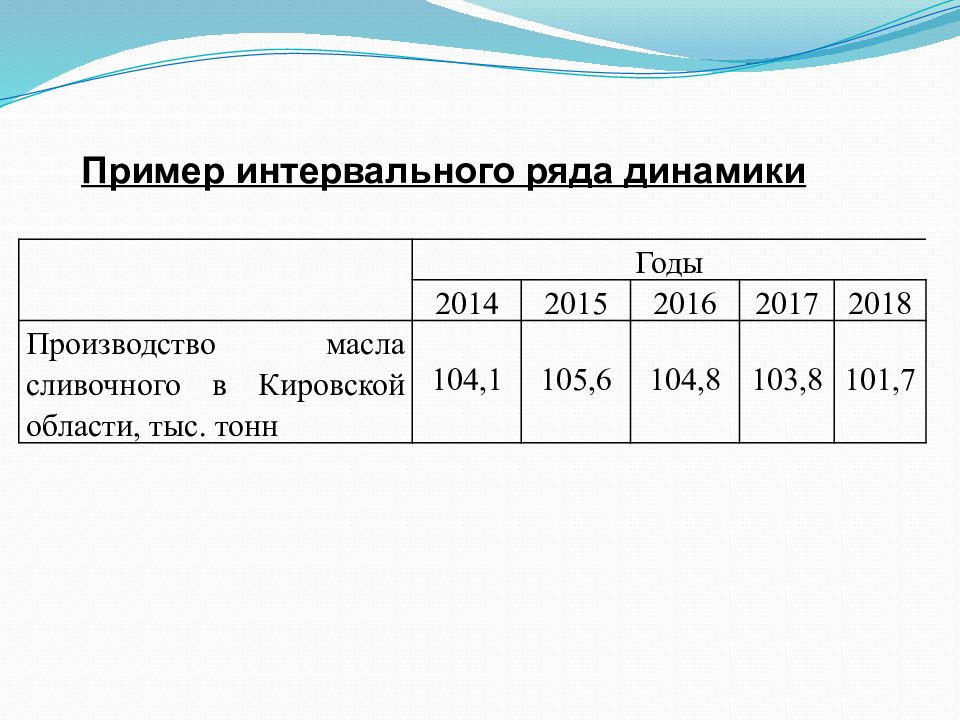
Годы 2014 2015 2016 2017 2018 Производство масла сливочного в Кировской области, тыс. тонн 104,1 105,6 104,8 103,8 101,7 Пример интервального ряда динамики
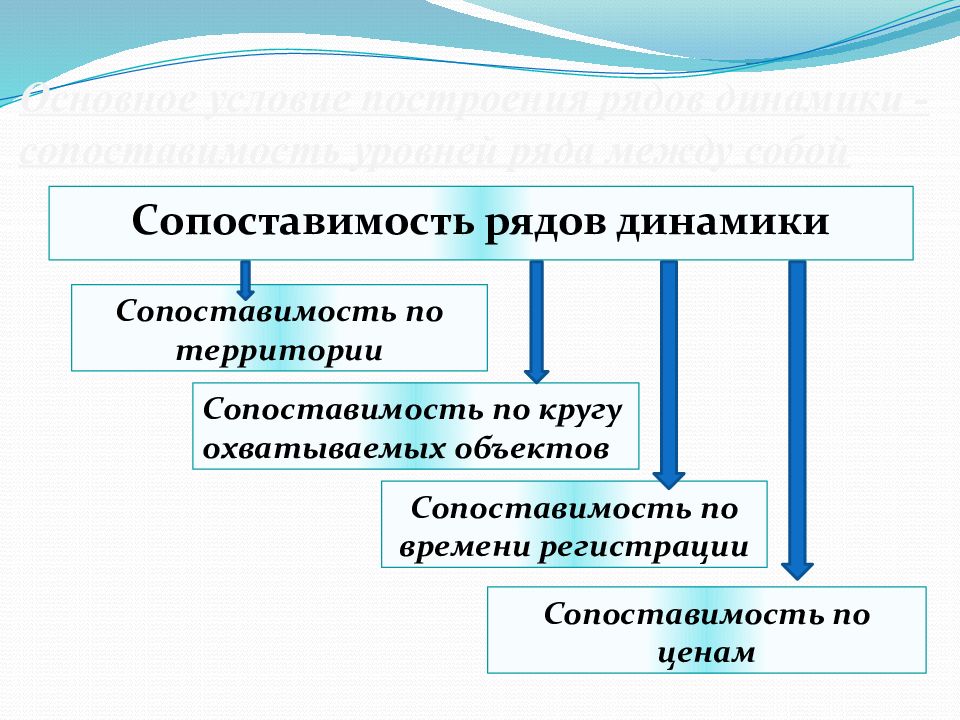
Сопоставимость рядов динамики Сопоставимость по кругу охватываемых объектов Сопоставимость по времени регистрации Сопоставимость по ценам Сопоставимость по территории
12 Статистическое изучение динамики социально-экономических явлений позволяет решать следующие основные задачи : 1)измерить скорость изменения уровней за определенный промежуток времени; 2)выявить и численно характеризовать основные тенденции развития изучаемых явлений во времени; 3)выявить факторы, обуславливающие такие изменения; 4) о пределить прогнозы развития явления в будущем.
13 2.Базисные и цепные показатели динамика.
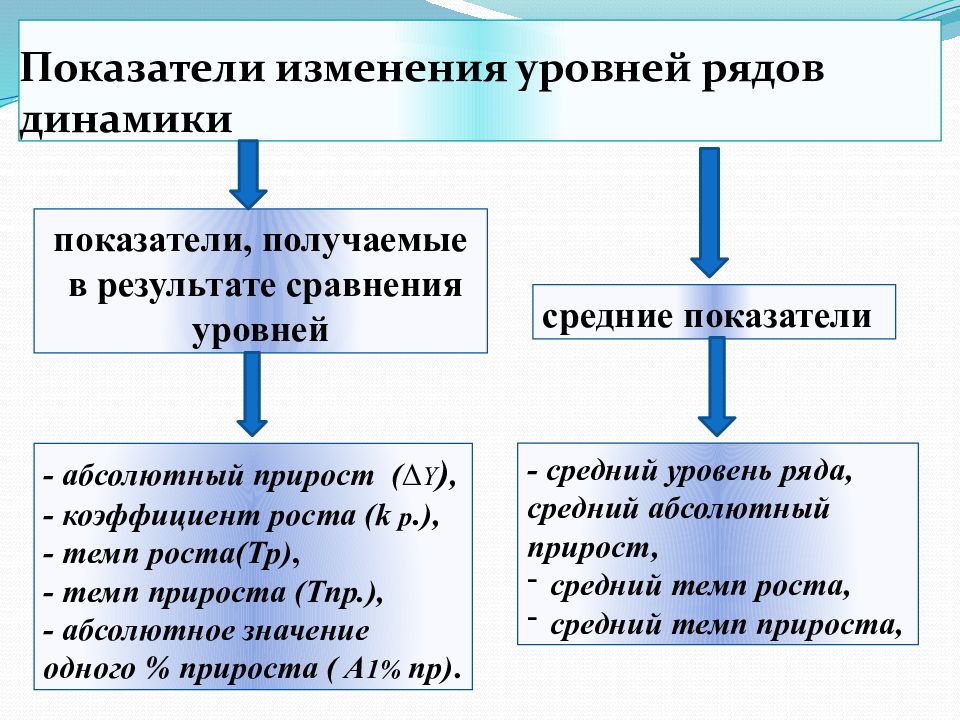
показатели, получаемые в результате сравнения уровней средние показатели - абсолютный прирост ( ∆ Y ), - коэффициент роста ( k р.), - темп роста( T р ), - темп прироста ( Тпр.), - абсолютное значение одного % прироста ( A 1% пр ). - средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста,
15 Для характеристики изменения уровней ряда динамики во времени определяют систему базисных и цепных показателей. Базисные показатели определяют при сравнении каждого последующего уровня ряда с принятым за базу ( обычно начальным ) уровнем. При расчете цепных показателей каждый последующий уровень сравнивают с предыдущим.
Где: Y i - уровень сравниваемого периода; Y i -1 - уровень предшествующего периода. Абсолютный прирост (цепной) ∆Y ц = Y i - Y i -1 Абсолютный прирост (базисный) ∆Y б = Y i - Y 0 Y 0 - уровень базисного периода
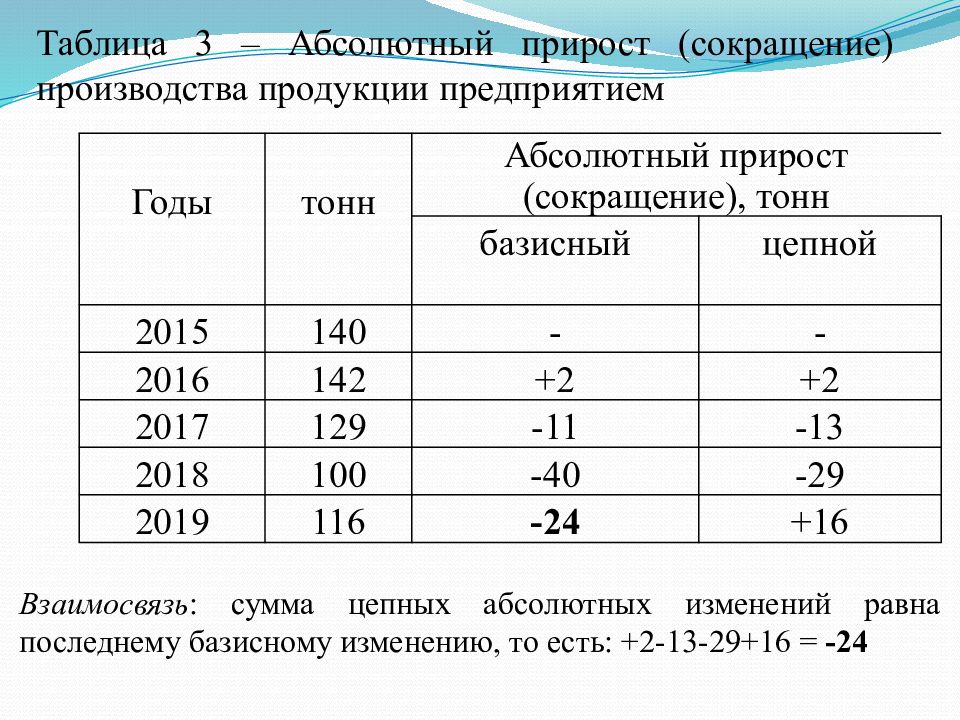
Взаимосвязь : сумма цепных абсолютных изменений равна последнему базисному изменению, то есть: +2-13-29+16 = -24 Годы тонн Абсолютный прирост (сокращение), тонн базисный цепной 2015 140 - - 2016 142 +2 +2 2017 129 -11 -13 2018 100 -40 -29 2019 116 -24 +16 Таблица 3 – Абсолютный прирост (сокращение) производства продукции предприятием
2. Темп и коэффициент роста (снижения) Коэффициент роста представляет собой кратное отношение сравниваемого уровня к предыдущему или базисному.
20 Темп роста (снижения)– это отношение сравниваемого уровня к предыдущему, или базисному, выраженное в %. Его можно также определить путем умножения коэффициента роста на 100%.
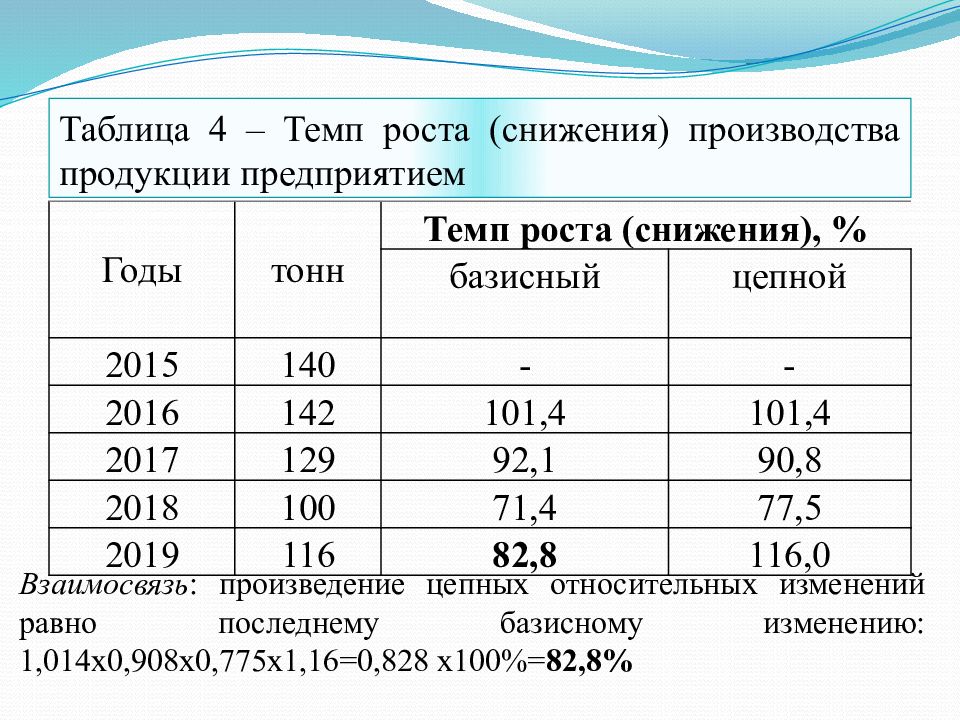
Взаимосвязь : произведение цепных относительных изменений равно последнему базисному изменению: 1,014х0,908х0,775х1,16=0,828 х100%= 82,8% Годы тонн Темп роста (снижения), % базисный цепной 2015 140 - - 2016 142 101,4 101,4 2017 129 92,1 90,8 2018 100 71,4 77,5 2019 116 82,8 116,0 Таблица 4 – Темп роста (снижения) производства продукции предприятием
22 3. Темп прироста (сокращения) показывает, на сколько % сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к уровню предыдущему или базисному. Этот показатель можно также определить путем вычитания 100% из темпа роста: Т прир. =Т р. - 100%
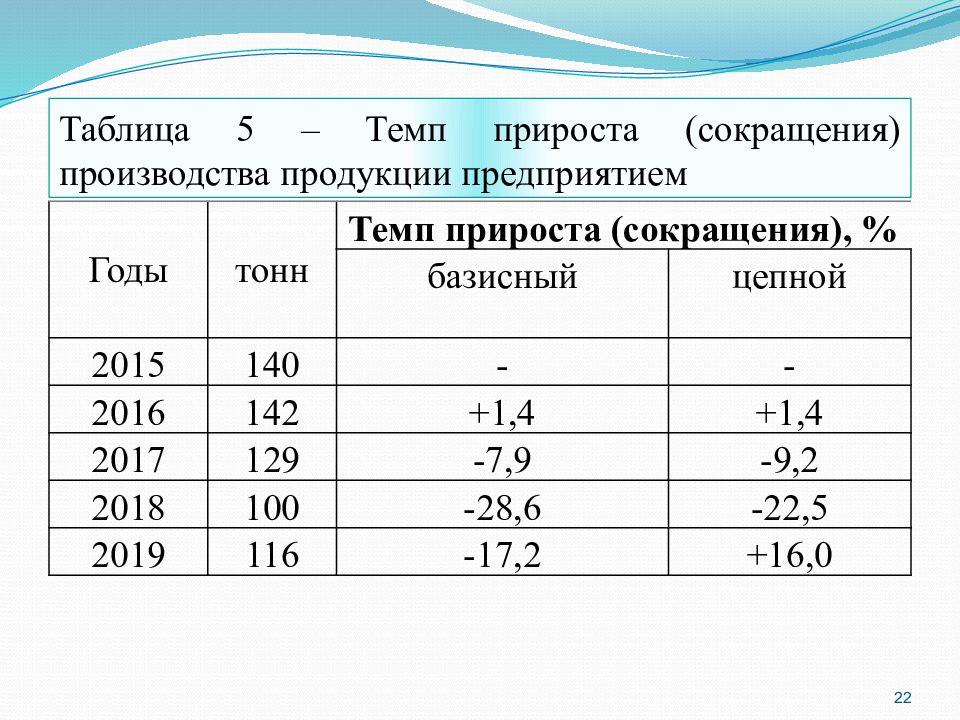
22 Годы тонн Темп прироста (сокращения), % базисный цепной 2015 140 - - 2016 142 +1,4 +1,4 2017 129 -7,9 -9,2 2018 100 -28,6 -22,5 2019 116 -17,2 +16,0 Таблица 5 – Темп прироста (сокращения) производства продукции предприятием
Данный показатель рассчитывают по формуле
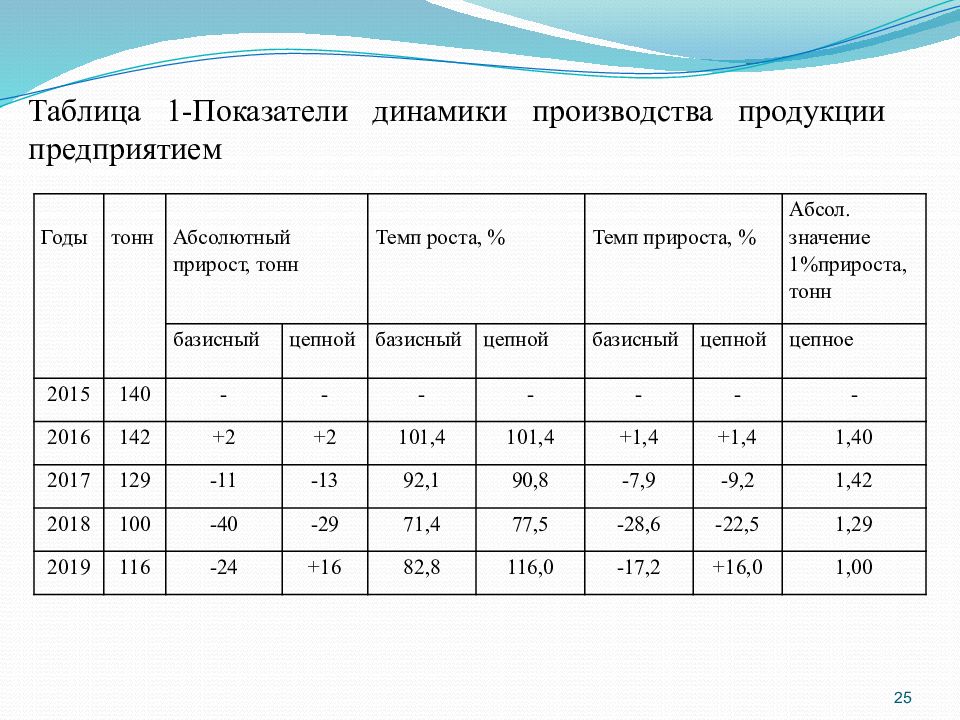
25 Годы тонн Абсолютный прирост, тонн Темп роста, % Темп прироста, % Абсол. значение 1%прироста, тонн базисный цепной базисный цепной базисный цепной цепное 2015 140 - - - - - - - 2016 142 +2 +2 101,4 101,4 +1,4 +1,4 1,40 2017 129 -11 -13 92,1 90,8 -7,9 -9,2 1,42 2018 100 -40 -29 71,4 77,5 -28,6 -22,5 1,29 2019 116 -24 +16 82,8 116,0 -17,2 +16,0 1,00 Таблица 1-Показатели динамики производства продукции предприятием
26 3.Средние уровни и показатели динамики.
27 Средний уровень интервального ряда динамики с равными интервалами определяется по формуле средней арифметической простой : п - число уровней ряда.
28 Средний уровень моментного ряда динамики определяется по формуле средней хронологической : .
29
30 Средний абсолютный прирост определяется по формуле: Среднегодовой абсолютный прирост составит : (по д анным таблиц 3 – 5)
31 Средний темп роста определяется: . Или, используется формула средней геометрической: Где Т 1, Т 2,… Т т – цепные темпы роста ; m - число темпов.
32 Среднегодовой темп роста будет равен (по данным таблиц 3 – 5) : . Среднегодовой темп прироста:
33 4.Выявление основной тенденции развития социально-экономических явлений.
34 Для выявления основной тенденции, т.е. закономерности изменения уровней динамического ряда, используются различные способы выравнивания, или сглаживания уровней. Сущность различных приемов выравнивания сводится к замене фактических уровней временного ряда расчетными, в меньшей степени подверженными случайным колебаниям.
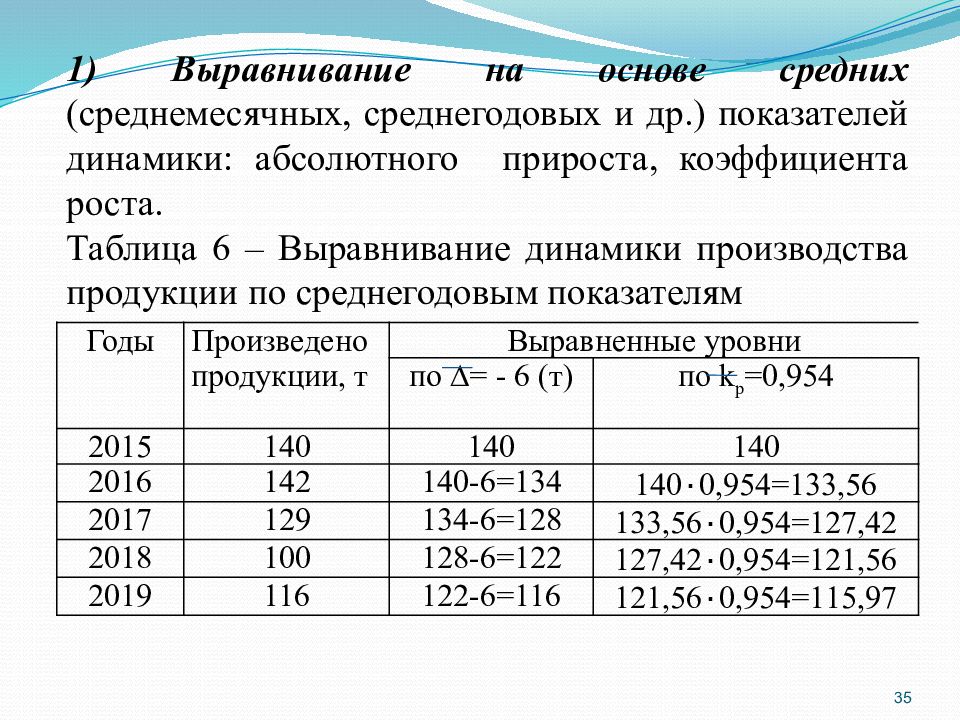
35 Годы Произведено продукции, т Выравненные уровни по ∆= - 6 (т) по k р =0,954 2015 140 140 140 2016 142 140-6=134 140 ٠ 0,954=133,56 2017 129 134-6=128 133,56 ٠ 0,954=127,42 2018 100 128-6=122 127,42 ٠ 0,954=121,56 2019 116 122-6=116 121,56 ٠ 0,954=115,97 1) Выравнивание на основе средних (среднемесячных, среднегодовых и др.) показателей динамики: абсолютного прироста, коэффициента роста. Таблица 6 – Выравнивание динамики производства продукции по среднегодовым показателям
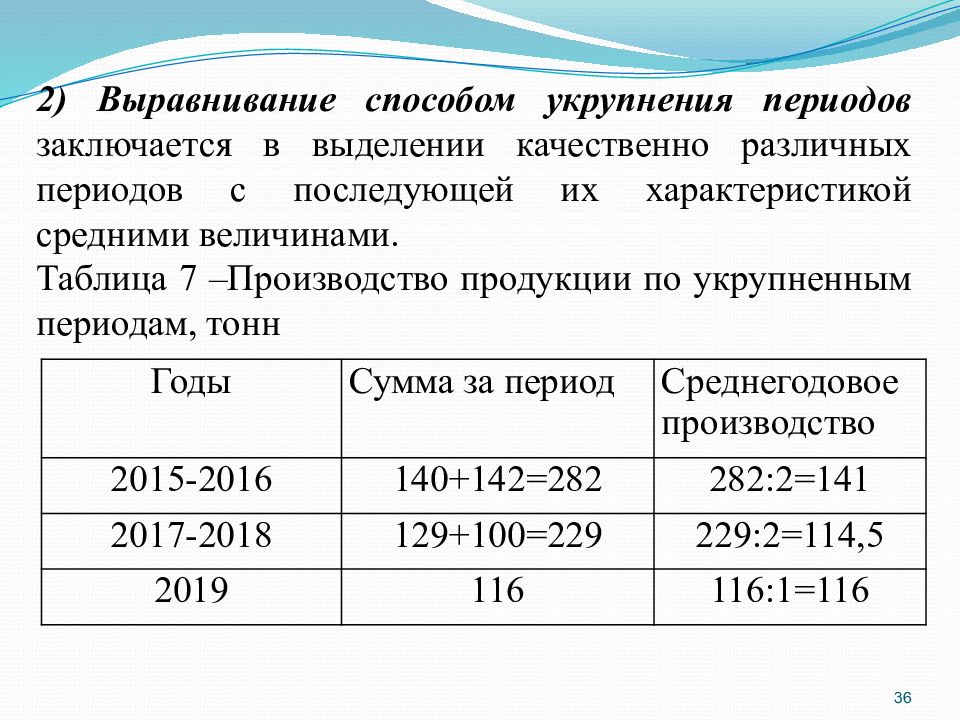
36 Годы Сумма за период Среднегодовое производство 2015-2016 140+142=282 282:2=141 2017-2018 129+100=229 229:2=114,5 2019 116 116:1=116 2) Выравнивание способом укрупнения периодов заключается в выделении качественно различных периодов с последующей их характеристикой средними величинами. Таблица 7 –Производство продукции по укрупненным периодам, тонн
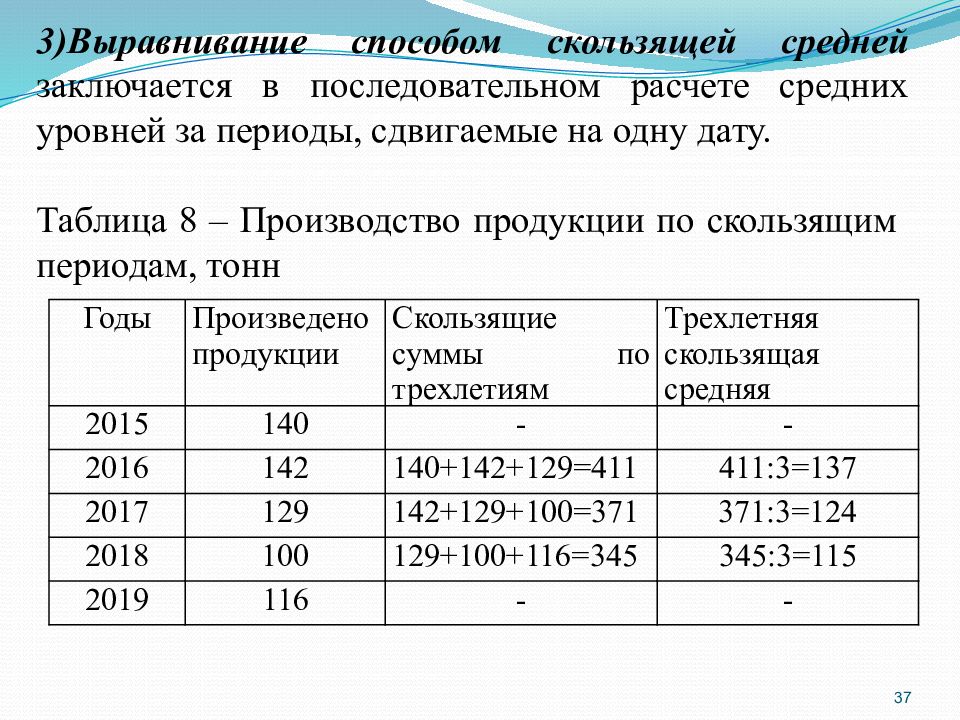
37 Годы Произведено продукции Скользящие суммы по трехлетиям Трехлетняя скользящая средняя 2015 140 - - 2016 142 140+142+129=411 411:3=137 2017 129 142+129+100=371 371:3=124 2018 100 129+100+116=345 345:3=115 2019 116 - - 3)Выравнивание способом скользящей средней заключается в последовательном расчете средних уровней за периоды, сдвигаемые на одну дату. Таблица 8 – Производство продукции по скользящим периодам, тонн
38
39 Рисунок 1 – Динамика производства продукции предприятием
40
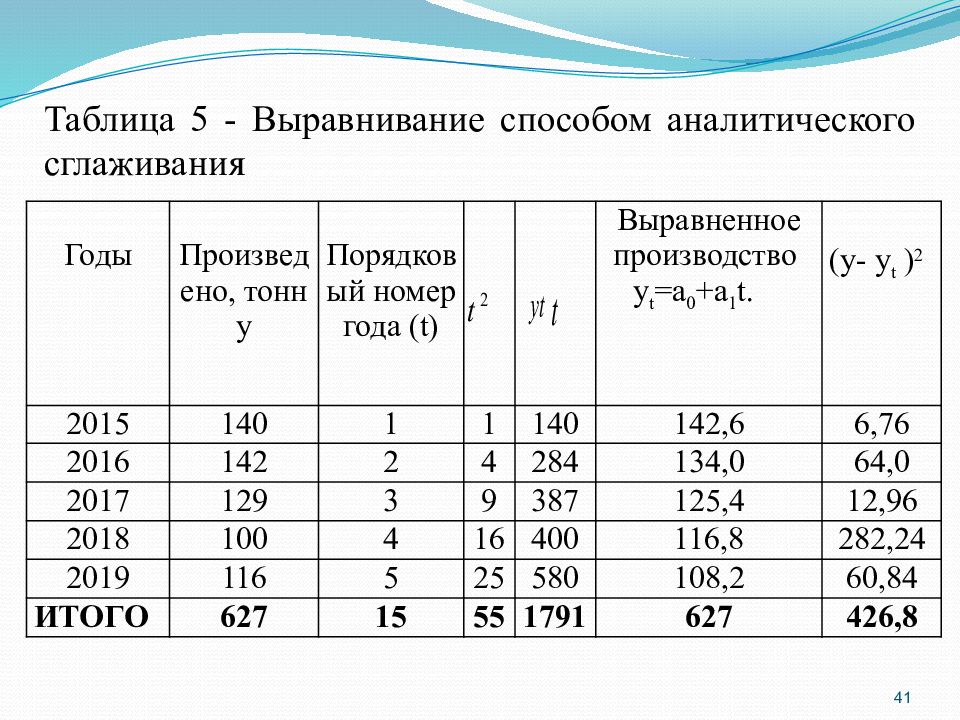
41 Годы Произведено, тонн у Порядковый номер года ( t ) Выравненное производство у t =а 0 +а 1 t. ( у- у t ) 2 2015 140 1 1 140 142,6 6,76 2016 142 2 4 284 134,0 64,0 2017 129 3 9 387 125,4 12,96 2018 100 4 16 400 116,8 282,24 2019 116 5 25 580 108,2 60,84 ИТОГО 627 15 55 1791 627 426,8 Таблица 5 - Выравнивание способом аналитического сглаживания
42
43 Для оценки степени приближения выравненных уровней к исходным определяют величину остаточного среднего квадратического отклонения. Следовательно, выравненные уровни отклоняются от исходных в среднем на 9,2 тонны, что составляет 7,3% относительно среднего уровня ряда, равного 125,4 тонны (627:5=125,4).
44
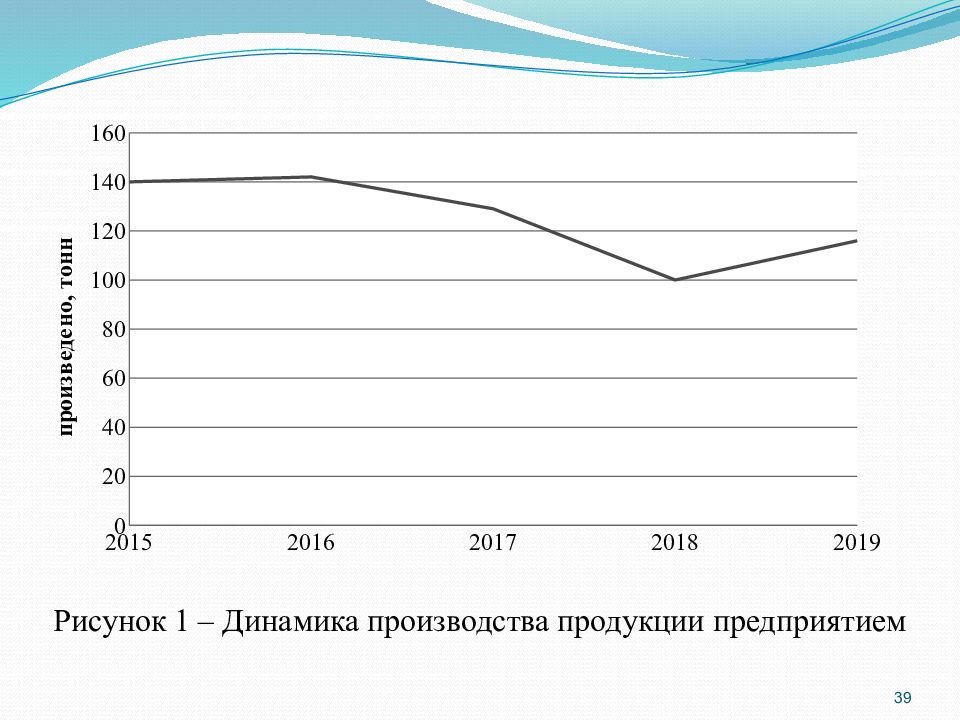
45 Анализ сезонных колебаний. Сезонные колебания – это регулярно повторяющиеся подъемы и снижения уровней ряда динамики на протяжении ряда лет. Сезонность имеет место в различных отраслях экономики: в торговле, сельском хозяйстве, строительстве, транспорте и других. Сезонность в изменении явлений можно наглядно представить на графике, построив сезонную волну.
46 Количественная оценка сезонности может быть дана при помощи индекса сезонности. Он равен отношению среднего уровня для каждого месяца, или квартала по данным за последние 2-3 года к общему среднемесячному, или среднеквартальному уровню
47 Пример.Имеются данные о реализации торговым предприятием товара «А» в течение 3-х лет. Определим индексы сезонности продаж данного товара по отдельным кварталам. Таблица 6- Сезонность реализация товара «А», штук Квартал Номер года 1 2 3 1 25 30 26 27 30,6 2 125 120 130 125 141,6 3 180 160 182 174 197,2 4 30 20 31 27 30,6 ИТОГО В СРЕДНЕМ 360 90 330 82,5 369 92,3 Х 88,25 Х = (360+330+369): 12 = 88,25 (штук).
48 Рисунок 2-Сезоннось продаж товара по кварталам в течение 3-х лет Полученные показатели сезонности могут быть использованы при прогнозировании. Допустим, в следующем году планируется реализовать 380 штук, среднеквартальный объем продаж составит 95 штук. С учетом сезонности он может составить: 1-ый квартал: (95 ٠ 30,6) :100=29(штук) 2-ый квартал: (95 ٠ 141,7) :100=135(штук) 3-ый квартал: (95 ٠ 197,2) :100=187(штук) 4-ый квартал: (95 ٠ 30,6) :100=29(штук).
