Первый слайд презентации: Ряды динамики
2005 2006 2007 2008 2009 Число вновь зарегистриро-ванных организаций 2041 2674 2157 2308 1673
- показатели времени, т.е. периоды или моменты, к которым относятся статистические данные ( t ); - сами значения статистических показателей, которые называются уровнями динамического ряда ( у ).
Слайд 4: Виды рядов динамики
интервальные моментные одномерные многомерные Динамические ряды могут быть построены по абсолютным, относительным или средним величинам.
Слайд 5: Сопоставимость
Изменение единиц измерения Изменение методологии учета или расчета показателей Переход объектов из одной категории в другую Изменение территориальных границ областей, районов Одинаковый экономический смысл уровней ряда
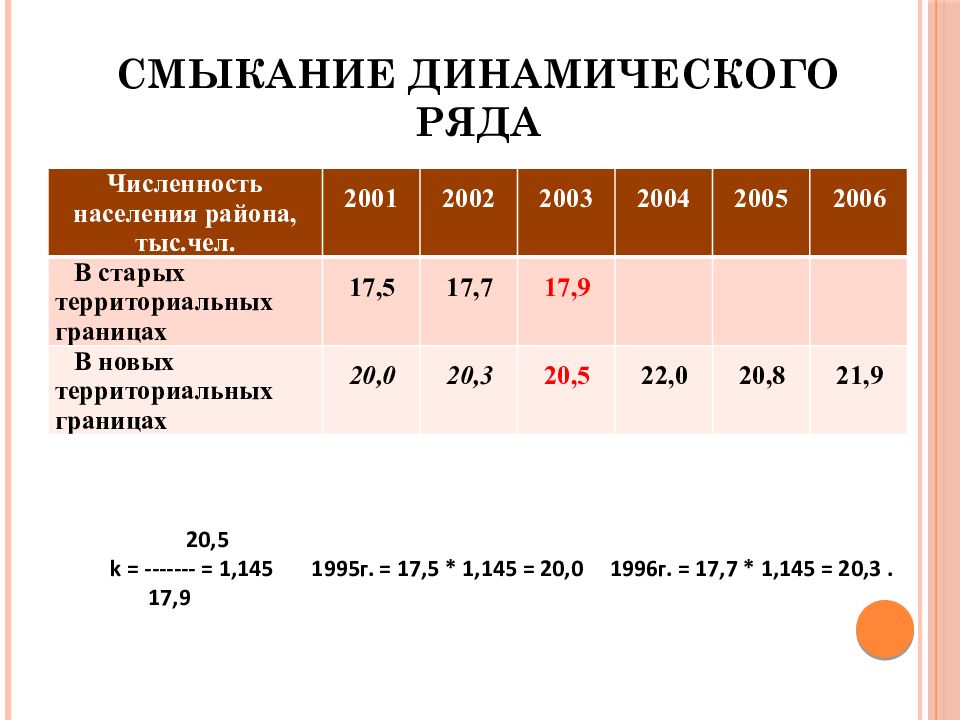
Слайд 6: Смыкание динамического ряда
Численность населения района, тыс.чел. 2001 2002 2003 2004 2005 2006 В старых территориальных границах 17,5 17,7 17,9 В новых территориальных границах 20,0 20,3 20,5 22,0 20,8 21,9 20,5 k = ------- = 1,145 1995 г. = 17,5 * 1,145 = 20,0 1996 г. = 17,7 * 1,145 = 20,3. 17,9
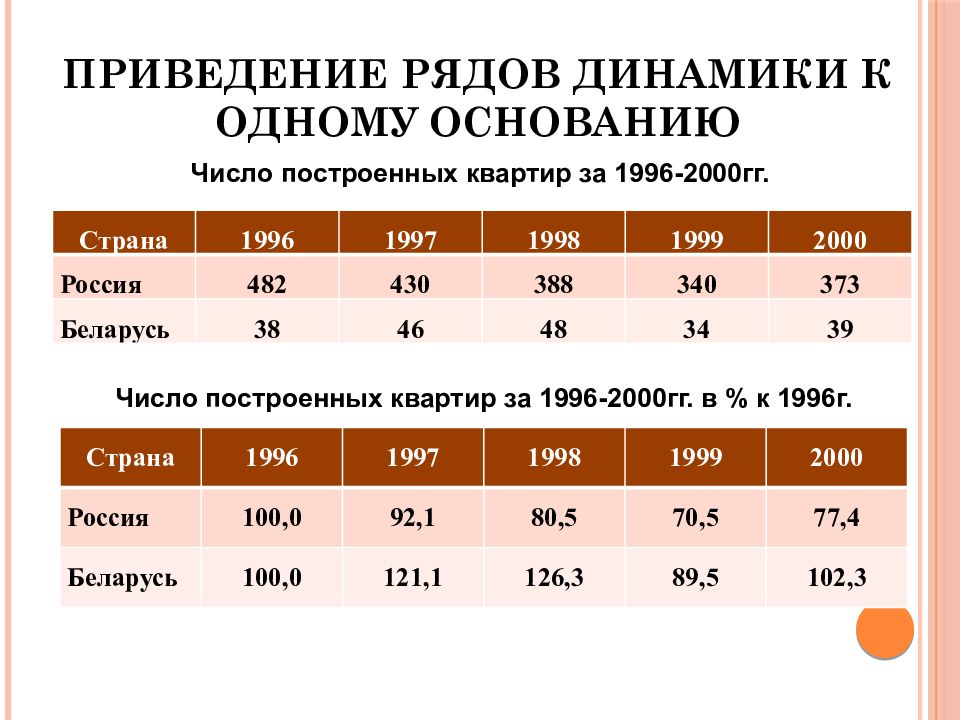
Слайд 7: Приведение рядов динамики к одному основанию
Страна 1996 1997 1998 1999 2000 Россия 482 430 388 340 373 Беларусь 38 46 48 34 39 Страна 1996 1997 1998 1999 2000 Россия 100,0 92,1 80,5 70,5 77,4 Беларусь 100,0 121,1 126,3 89,5 102,3 Число построенных квартир за 1996-2000гг. в % к 1996г. Число построенных квартир за 1996-2000гг.
Слайд 8: Аналитические показатели анализа динамических рядов
Абсолютные : средний уровень динамического ряда; абсолютные приросты: цепные и базисные, средний абсолютный прирост. Относительные : темпы роста: цепные и базисные, средний темп роста; темпы прироста: цепные и базисные, средний темп прироста; абсолютное значение одного процента прироста.
Слайд 9
Цепные и базисные показатели вычисляются для характеристики изменения уровней динамического ряда и различаются между собой базами сравнения: цепные рассчитываются по отношению к предыдущему уровню (переменная база сравнения), базисные – к уровню, принятому за базу сравнения (постоянная база сравнения).
Слайд 10
Средние показатели ряда динамики представляют собой обобщенные характеристики ряда динамики за рассматриваемый период. С их помощью сравнивают интенсивность развития явления по отношению к различным объектам, например по странам, отраслям, предприятиям и т.д., или периодам времени.
Слайд 11: Показатели абсолютного изменения уровней динамического ряда
Абсолютные приросты рассчитываются как разность между двумя значениями соседних уровней динамического ряда (цепные приросты) или как разность между значениями текущего уровня и уровня, принятого за базу сравнения (базисные приросты) и выражаются в тех же единицах измерения, что и уровни динамического ряда.
Слайд 12: цепной абсолютный прирост
где y i - 1 - уровень, предшествующий i - му уровню динамического ряда.
Слайд 13: Базисный абсолютный прирост
где y i - i -й текущий уровень ряда, y 0 - уровень ряда динамики, принятый за базу сравнения.
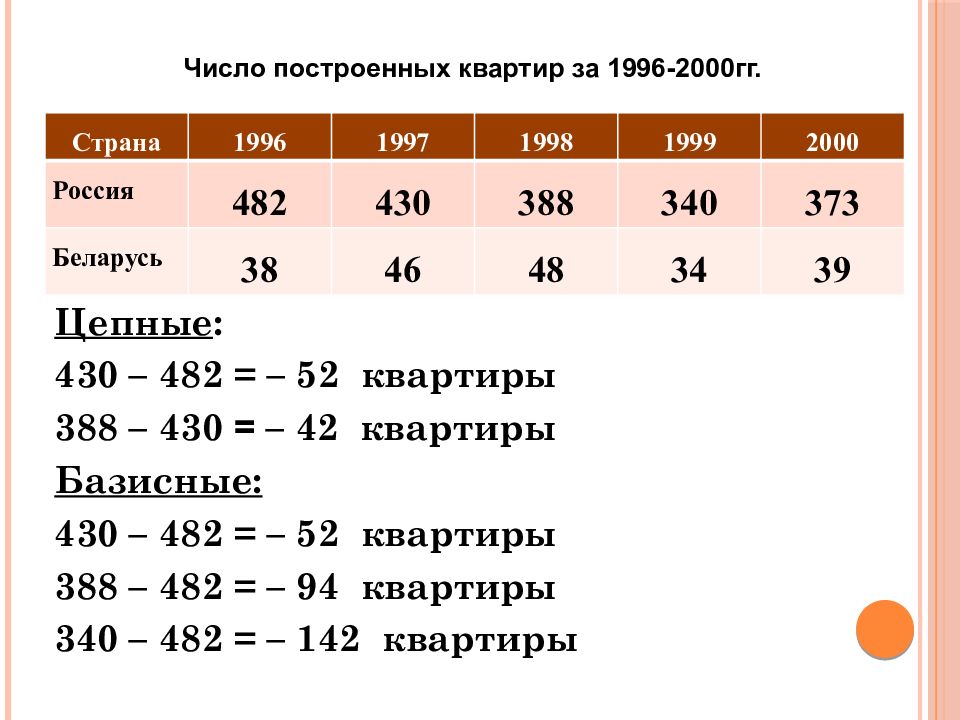
Слайд 14
Страна 1996 1997 1998 1999 2000 Россия 482 430 388 340 373 Беларусь 38 46 48 34 39 Число построенных квартир за 1996-2000гг. Цепные : 430 – 482 = – 52 квартиры 388 – 430 = – 42 квартиры Базисные: 430 – 482 = – 52 квартиры 388 – 482 = – 94 квартиры 340 – 482 = – 142 квартиры
Слайд 15
Средний абсолютный прирост показывает, на сколько единиц в среднем ежемесячно, или ежеквартально, или ежегодно и т.д. изменялось значение показателя в течение рассматриваемого периода времени. 1) где, - цепные абсолютные приросты показателя; 2) где y n - последний уровень ряда.
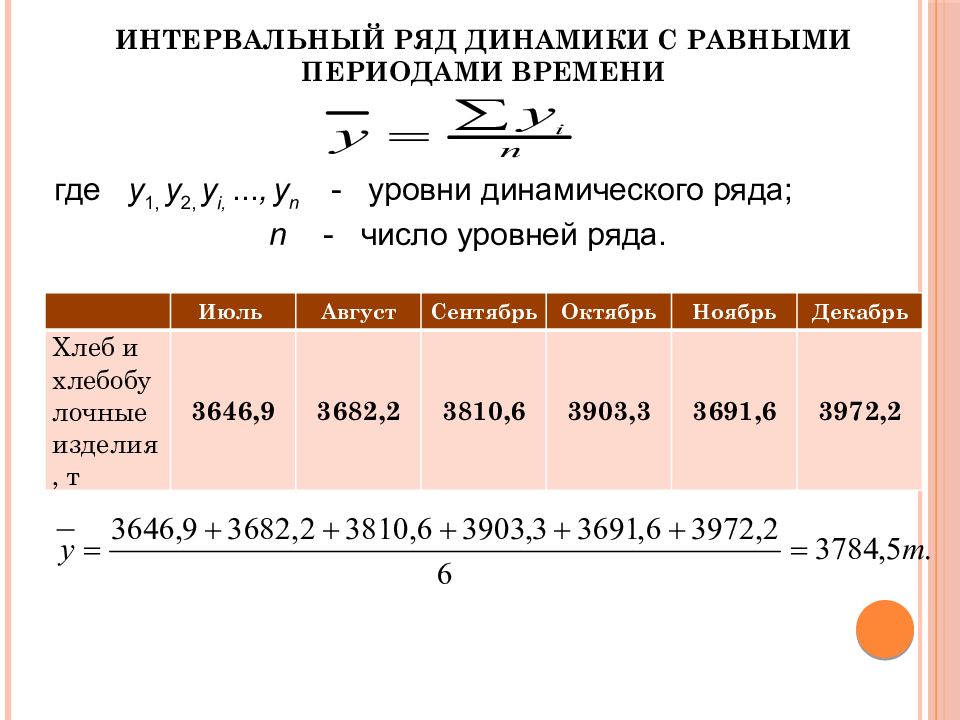
Слайд 16: интервальный ряд динамики с равными периодами времени
где y 1, y 2, y i,..., y n - уровни динамического ряда; n - число уровней ряда. Июль Август Сентябрь Октябрь Ноябрь Декабрь Хлеб и хлебобулочные изделия, т 3646,9 3682,2 3810,6 3903,3 3691,6 3972,2
Слайд 17: Интервальный ряд динамики с неравными периодами времени
с 1-го по 18-е число месяца на предприятии работали 45 человек, с 19-го по 27-е – 48 человек, с 28-го по 31-е число – 54 человека, то среднесписочное число работников за месяц составит:
Слайд 18: Моментный ряд с одинаковыми временными промежутками
Дата 01.01.09 01.02.09 01.03.09 01.04.09 Остаток денежных средств, руб. 132 000 147 289 151 870 148 500
Слайд 19: Моментный ряд с неравными временными промежутками
01.01.09 01.02.09 01.03.09 01.07.09 01.09.09 01.12.09 01.01.10 Запасы товаров, тыс.р. 1320 1472 1518 1300 1100 1005 920
Слайд 20: Показатели относительного изменения уровней динамического ряда
Коэффициент роста представляет собой соотношение двух уровней динамического ряда. Он показывает, во сколько раз изменилось значение показателя в одном периоде (моменте) времени по сравнению с другим. Темп роста – это коэффициент роста, выраженный в процентах. Он показывает, сколько процентов составляет значение показателя в данном периоде, если уровень, с которым приводится сравнение, принять за 100%.
Слайд 23
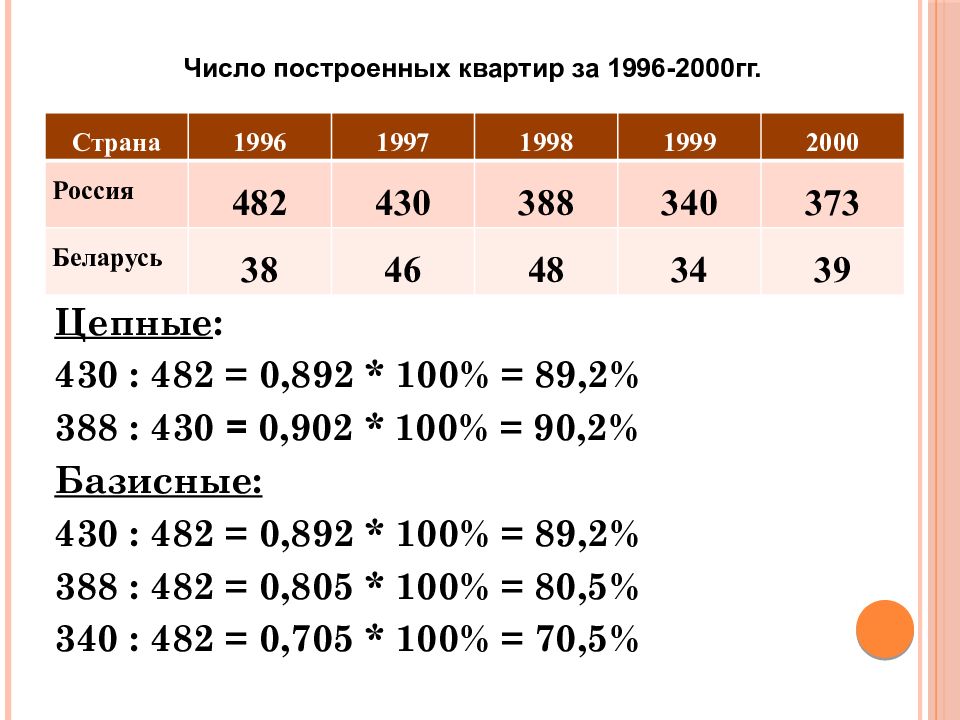
Страна 1996 1997 1998 1999 2000 Россия 482 430 388 340 373 Беларусь 38 46 48 34 39 Число построенных квартир за 1996-2000гг. Цепные : 430 : 482 = 0,892 * 100% = 89,2% 388 : 430 = 0,902 * 100% = 90,2% Базисные: 430 : 482 = 0,892 * 100% = 89,2% 388 : 482 = 0,805 * 100% = 80,5% 340 : 482 = 0,705 * 100% = 70,5%
Слайд 25
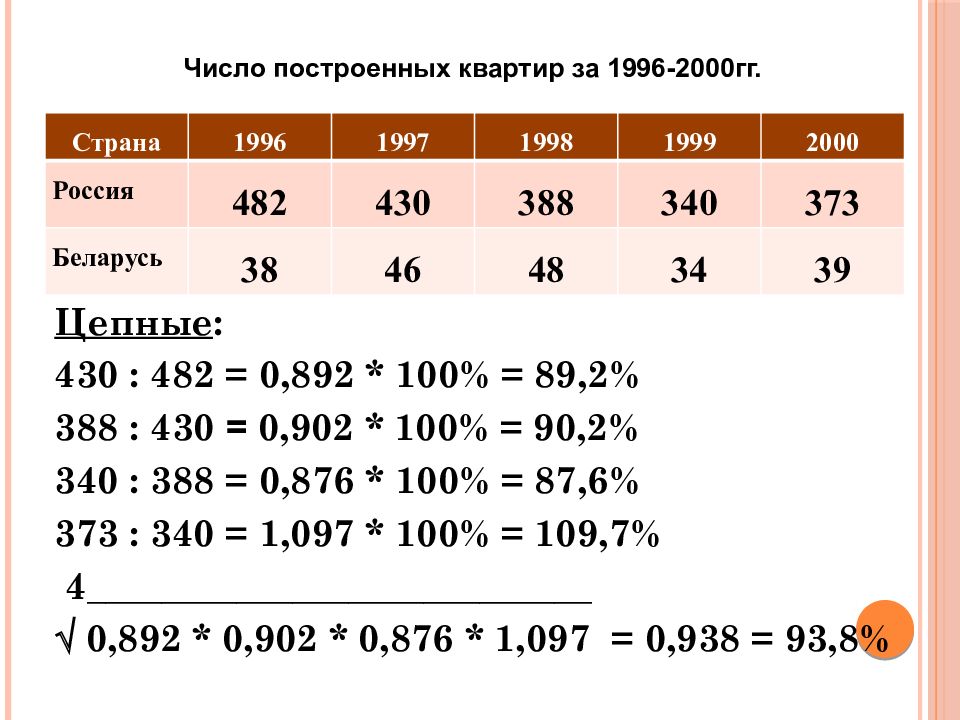
Страна 1996 1997 1998 1999 2000 Россия 482 430 388 340 373 Беларусь 38 46 48 34 39 Число построенных квартир за 1996-2000гг. Цепные : 430 : 482 = 0,892 * 100% = 89,2% 388 : 430 = 0,902 * 100% = 90,2% 340 : 388 = 0,876 * 100% = 87,6% 373 : 340 = 1,097 * 100% = 109,7% 4___________________________ 0,892 * 0,902 * 0,876 * 1,097 = 0,938 = 93,8%
Слайд 26: Темпы прироста
Цепные темпы прироста: Базисные темпы прироста: Средний темп прироста: Абсолютное значение 1% прироста:
Слайд 27
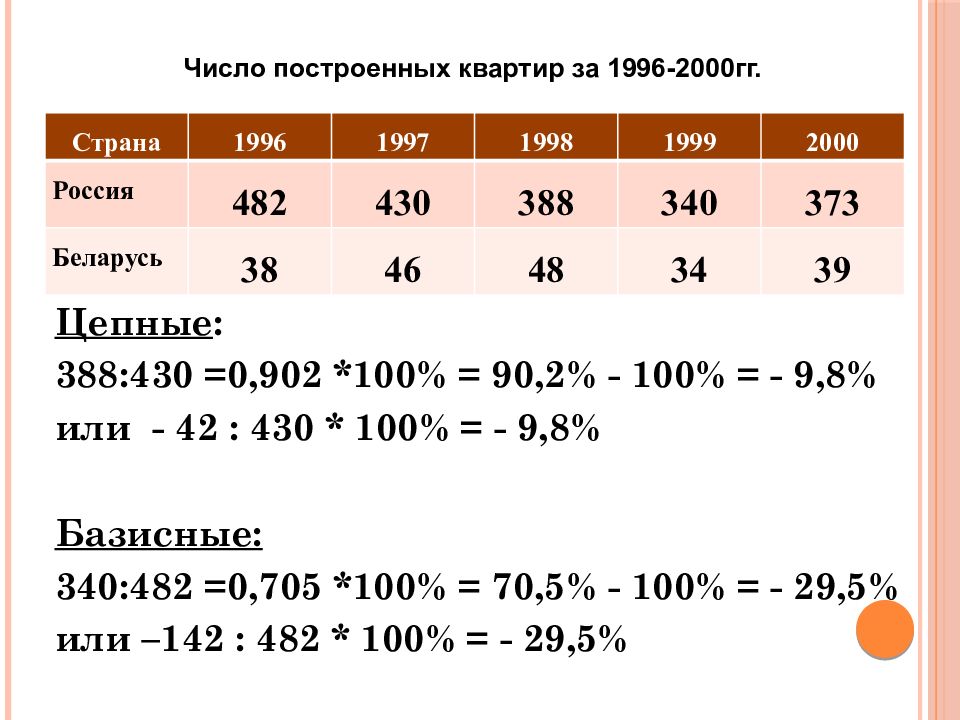
Страна 1996 1997 1998 1999 2000 Россия 482 430 388 340 373 Беларусь 38 46 48 34 39 Число построенных квартир за 1996-2000гг. Цепные : 388:430 = 0,9 0 2 *100% = 90,2% - 100% = - 9,8% или - 42 : 4 30 * 100% = - 9,8% Базисные: 340:482 = 0,705 *100% = 70,5% - 100% = - 29,5% или –142 : 482 * 100% = - 29,5%
Слайд 28: Методы анализа основной тенденции в рядах динамики
Факторы, влияющие на формирование уровней динамического ряда: действующие долговременно и определяющие основную тенденцию развития явления; действующие периодически – сезонные и циклические колебания; вызывающие случайные колебания уровней динамического ряда.
Слайд 29
Тенденция развития, или тренд, - это сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов.
Слайд 30: Методы анализа основной тенденции в рядах динамики
Метод укрупнения интервалов Метод скользящей средней Аналитическое выравнивание динамических рядов
Слайд 31: Метод укрупнения интервалов
Метод укрупнения интервалов. В этом случае исходный динамический ряд заменяется другим, показатели которого будут относиться к большим по продолжительности периодам времени.
Слайд 32: Метод скользящей средней
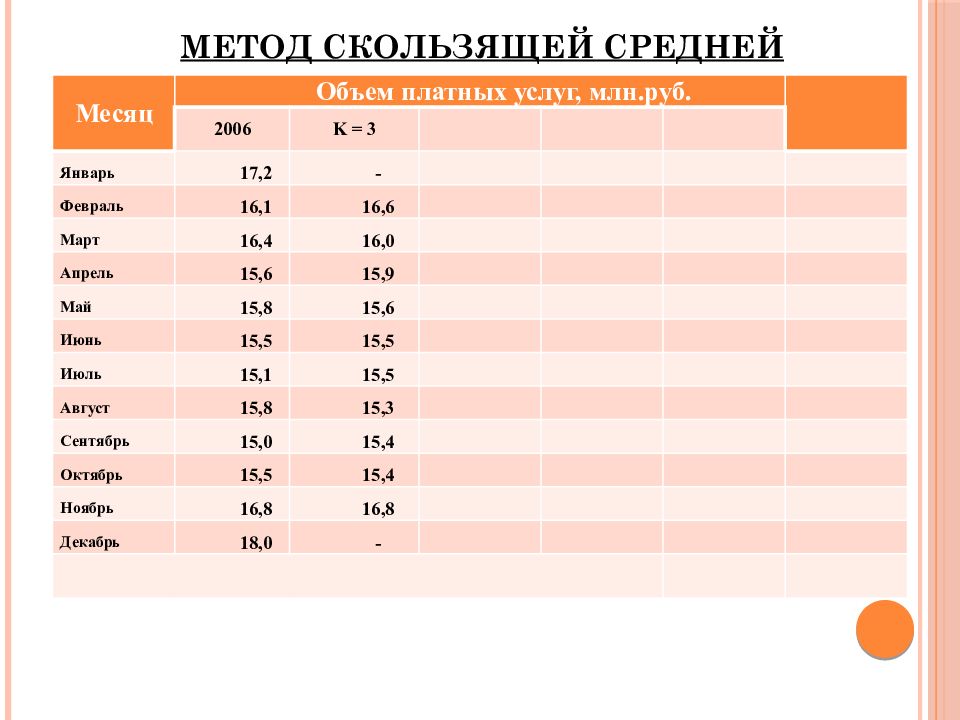
Метод скользящей средней. Для определения скользящей средней формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня динамического ряда на один уровень. По сформированным укрупненным интервалам определяется скользящая средняя, которая относится к середине укрупненного интервала. Таким образом, мы по исходным (эмпирическим) уровням определяем расчетные (теоретические) уровни. При этом посредством осреднения эмпирических данных индивидуальные колебания погашаются и общая тенденция развития явления выражается в виде некоторой плавной линии.
Слайд 33: Метод скользящей средней
Месяц Объем платных услуг, млн.руб. 2006 K = 3 Январь 17,2 - Февраль 16,1 16,6 Март 16,4 16,0 Апрель 15,6 15,9 Май 15,8 15,6 Июнь 15,5 15,5 Июль 15,1 15,5 Август 15,8 15,3 Сентябрь 15,0 15,4 Октябрь 15,5 15,4 Ноябрь 16,8 16,8 Декабрь 18,0 -
Слайд 34: Метод скользящей средней
Недостатки этого метода: сокращение сглаженного ряда с обоих концов на число уровней, равных k -1, где k - это число уровней, включенных в период сглаживания; произвольный выбор числа k.
Слайд 35: Аналитическое выравнивание динамических рядов
Линейная: Парабола 2-го порядка: Показательная: Гиперболическая:
Слайд 36
В первую очередь проводится анализ цепных абсолютных приростов и темпов прироста: если цепные абсолютные приросты относительно стабильны ( y ц const ), то в качестве формы тренда выбирают прямую линию: y t = a + b * t ; если относительно стабильными являются цепные темпы прироста ( Т ц const ), то в качестве формы тренда следует принять показательную кривую: y t = a * b t ; если цепные абсолютные приросты более или менее равномерно увеличиваются или уменьшаются, то в качестве формы тренда принимается уравнение параболы: y t = a + b * t + c * t 2.
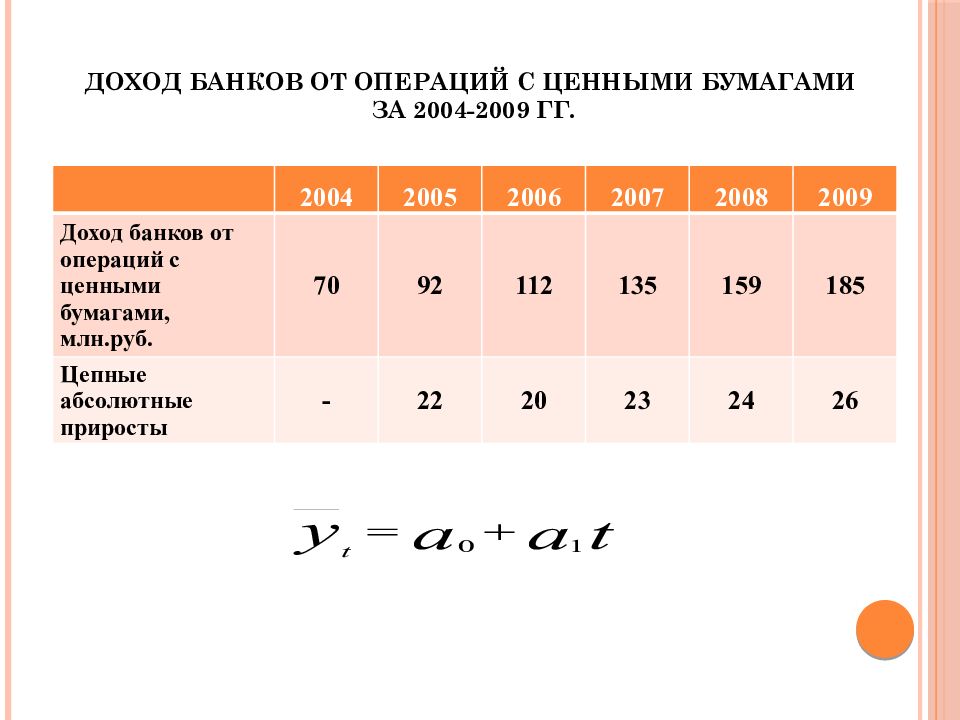
Слайд 37: Доход банков от операций с ценными бумагами за 2004-2009 гг
2004 2005 2006 2007 2008 2009 Доход банков от операций с ценными бумагами, млн.руб. 70 92 112 135 159 185 Цепные абсолютные приросты - 22 20 23 24 26
Слайд 38
После выбора вида кривой вычисляются ее параметры методом наименьших квадратов. Это означает, что из множества кривых данного вида нам надо отыскать ту, которая превращает в min сумму квадратов отклонений фактических уровней от расчетных: ( y i - y t ) 2 min.
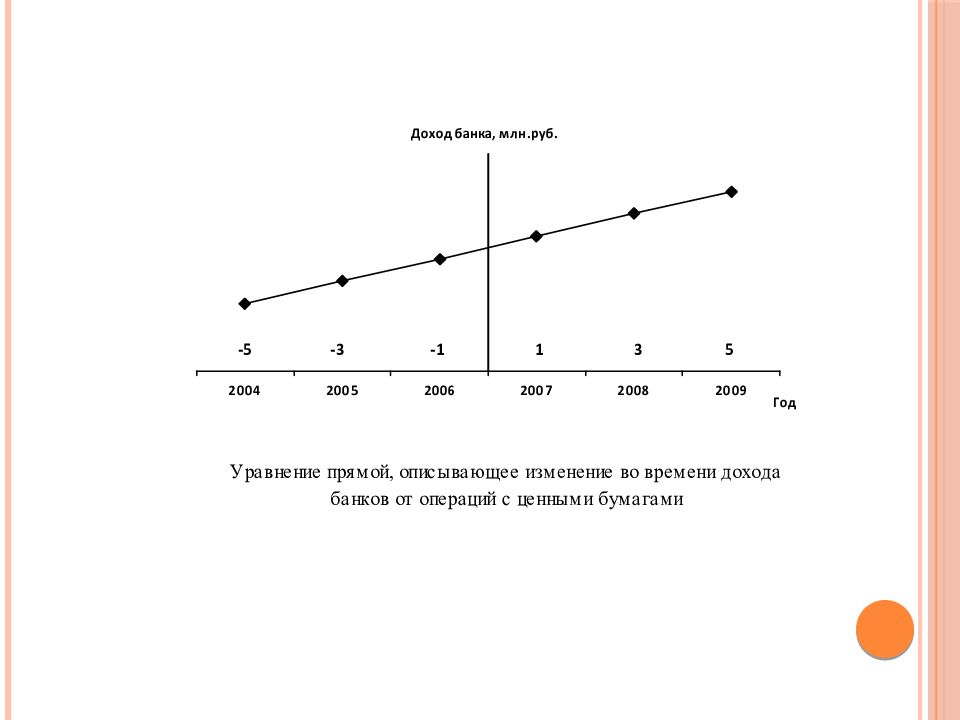
Слайд 39
Уравнение прямой: y t = a + b * t. При условии ( y i - y t ) 2 min нам необходимо решить систему двух нормальных уравнений: a 0 *n + a 1 * t = y a 0 * t + a 1 * t 2 = y*t.
Слайд 40
Для упрощения расчетов сделаем t = 0, тогда: a 0 *n = y a 1 * t 2 = y*t y y*t a 0 = -------- ; a 1 = -----------. n t 2
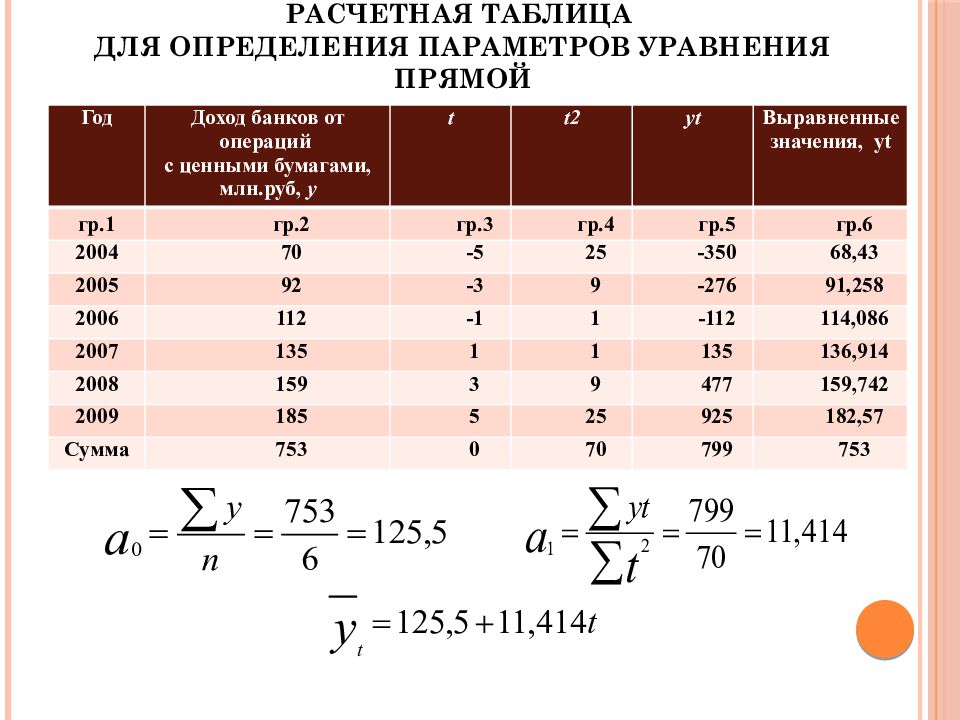
Слайд 41: Расчетная таблица для определения параметров уравнения прямой
Год Доход банков от операций с ценными бумагами, млн.руб, y t t2 yt Выравненные значения, yt гр.1 гр.2 гр.3 гр.4 гр.5 гр.6 2004 70 -5 25 -350 68,43 2005 92 -3 9 -276 91,258 2006 112 -1 1 -112 114,086 2007 135 1 1 135 136,914 2008 159 3 9 477 159,742 2009 185 5 25 925 182,57 Сумма 753 0 70 799 753
Слайд 43: C езонные колебания уровней динамического ряда
Под сезонными колебаниям и понимаются более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений.
Слайд 44: 2 способа определения индексов сезонности
1. Метод постоянной средней: 2. Метод переменной средней:
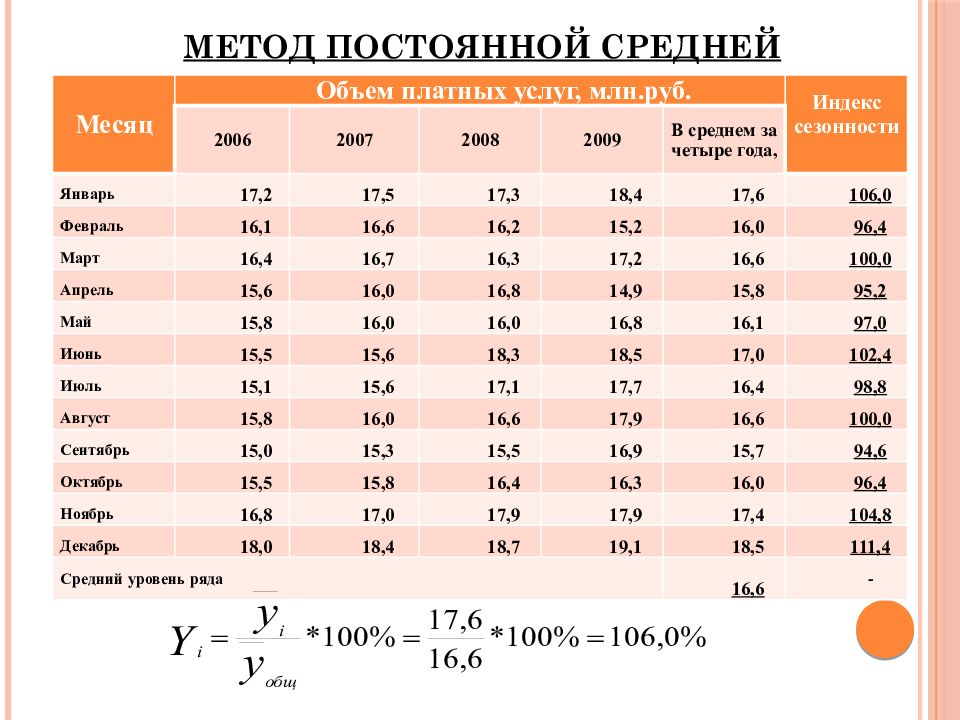
Слайд 45: Метод постоянной средней
Месяц Объем платных услуг, млн.руб. Индекс сезонности 2006 2007 2008 2009 В среднем за четыре года, Январь 17,2 17,5 17,3 18,4 17,6 106,0 Февраль 16,1 16,6 16,2 15,2 16,0 96,4 Март 16,4 16,7 16,3 17,2 16,6 100,0 Апрель 15,6 16,0 16,8 14,9 15,8 95,2 Май 15,8 16,0 16,0 16,8 16,1 97,0 Июнь 15,5 15,6 18,3 18,5 17,0 102,4 Июль 15,1 15,6 17,1 17,7 16,4 98,8 Август 15,8 16,0 16,6 17,9 16,6 100,0 Сентябрь 15,0 15,3 15,5 16,9 15,7 94,6 Октябрь 15,5 15,8 16,4 16,3 16,0 96,4 Ноябрь 16,8 17,0 17,9 17,9 17,4 104,8 Декабрь 18,0 18,4 18,7 19,1 18,5 111,4 Средний уровень ряда 16,6 -
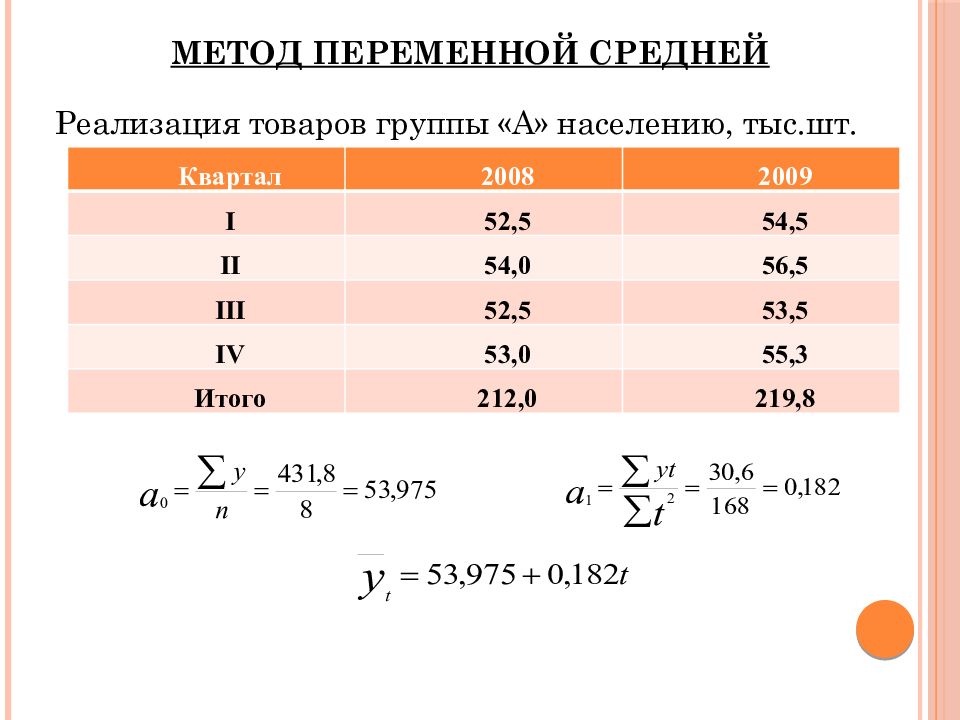
Слайд 46: Метод переменной средней
Реализация товаров группы «А» населению, тыс.шт. Квартал 2008 2009 I 52,5 54,5 II 54,0 56,5 III 52,5 53,5 IV 53,0 55,3 Итого 212,0 219,8
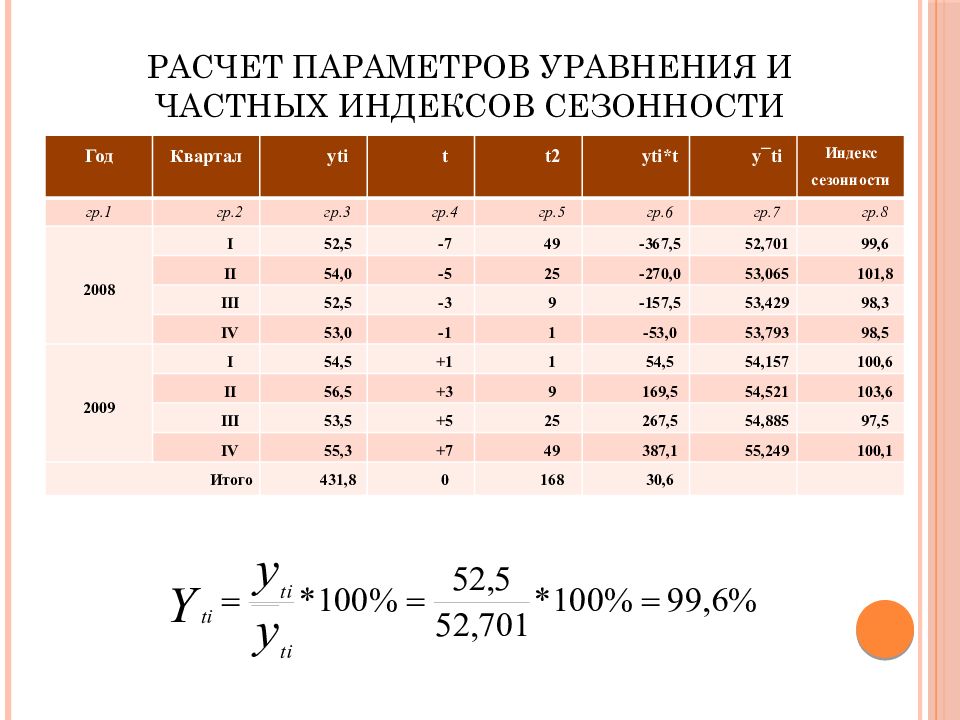
Слайд 47: Расчет параметров уравнения и частных индексов сезонности
Год Квартал yti t t2 yti *t y¯ti Индекс сезонности гр.1 гр.2 гр.3 гр.4 гр.5 гр.6 гр.7 гр.8 2008 I 52,5 -7 49 -367,5 52,701 99,6 II 54,0 -5 25 -270,0 53,065 101,8 III 52,5 -3 9 -157,5 53,429 98,3 IV 53,0 -1 1 -53,0 53,793 98,5 2009 I 54,5 +1 1 54,5 54,157 100,6 II 56,5 +3 9 169,5 54,521 103,6 III 53,5 +5 25 267,5 54,885 97,5 IV 55,3 +7 49 387,1 55,249 100,1 Итого 431,8 0 168 30,6
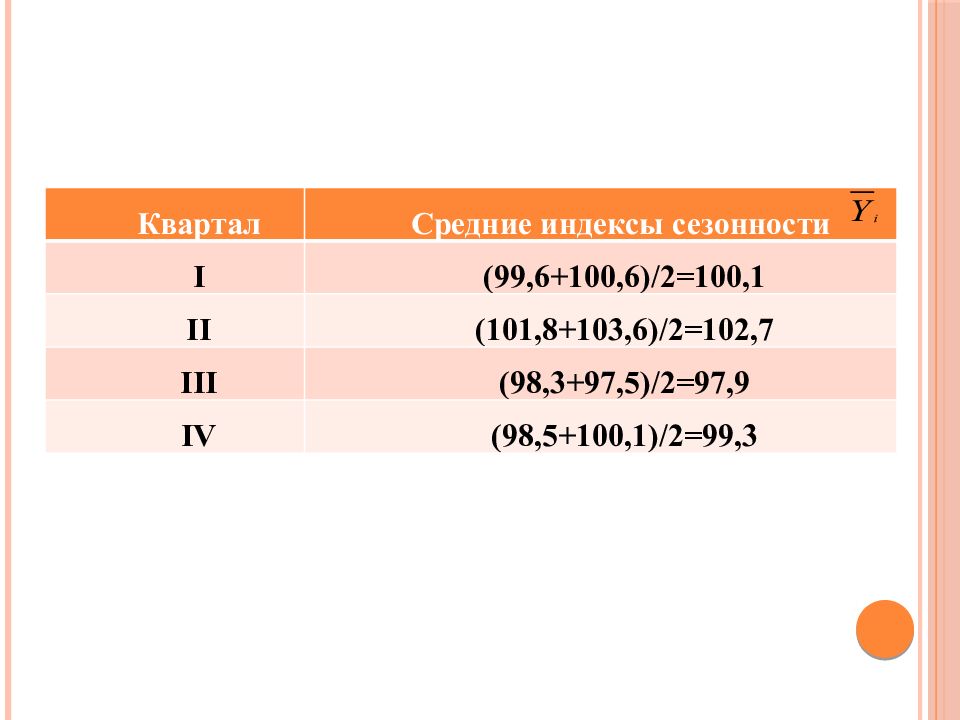
Слайд 48
Квартал Средние индексы сезонности I (99,6+100,6)/2=100,1 II (101,8+103,6)/2=102,7 III (98,3+97,5)/2=97,9 IV (98,5+100,1)/2=99,3
Слайд 49: Экстраполяция и интерполяция в рядах динамики
Под экстраполяцией понимается распространение выявленных при анализе динамических рядов закономерностей развития изучаемого явления на будущее. где l – срок прогноза; y n – конечный уровень базисного ряда динамики; y n + l – экстраполируемый уровень. Наряду с экстраполяцией применяется метод интерполяции, то есть получение данных внутри имеющихся.