Первый слайд презентации: ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
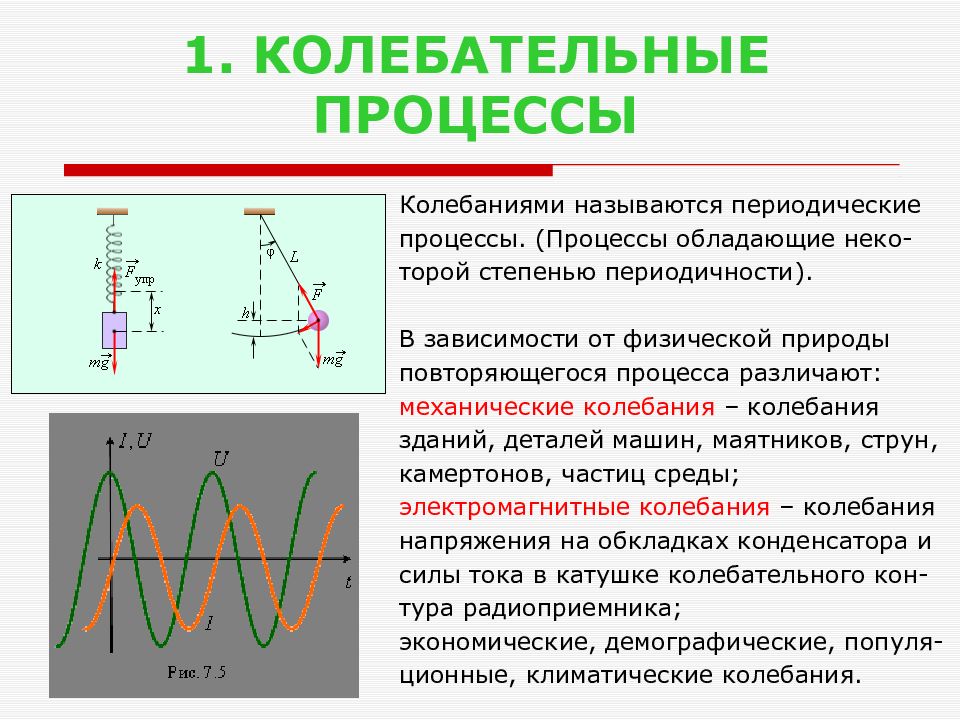
Слайд 2: 1. КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ
Колебаниями называются периодические процессы. (Процессы обладающие неко- торой степенью периодичности). В зависимости от физической природы повторяющегося процесса различают: механические колебания – колебания зданий, деталей машин, маятников, струн, камертонов, частиц среды; электромагнитные колебания – колебания напряжения на обкладках конденсатора и силы тока в катушке колебательного кон- тура радиоприемника; экономические, демографические, популя- ционные, климатические колебания.
Слайд 3: 2. КЛАССИФИКАЦИЯ КОЛЕБАНИЙ
В зависимости от характера воздей- ствия на колеблющуюся систему различают свободные (собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания. Свободными (или собственными), на- зываются колебания, которые проис- ходят в системе, предоставленной самой себе после того, как она была выведена из положения равновесия. Вынужденными называются колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодической силы.
Слайд 4: 3. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Простейшими являются гармоничес- кие колебания то есть такие, при которых колеблющаяся величина изменяется по гармоническому за- кону (синус или косинус). Система, в которой некоторая физическая величина совершает колебания по закону синуса или косинуса называется гармоническим осциллятором. Колебания в природе и технике часто имеют характер очень близкий к гармоническим. Негармонические периодические процессы могут быть представлены суммой гармонических колебаний.
Слайд 5: 4. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Рассмотрим колебания гармонического осциллятора. Они описываются уравнением
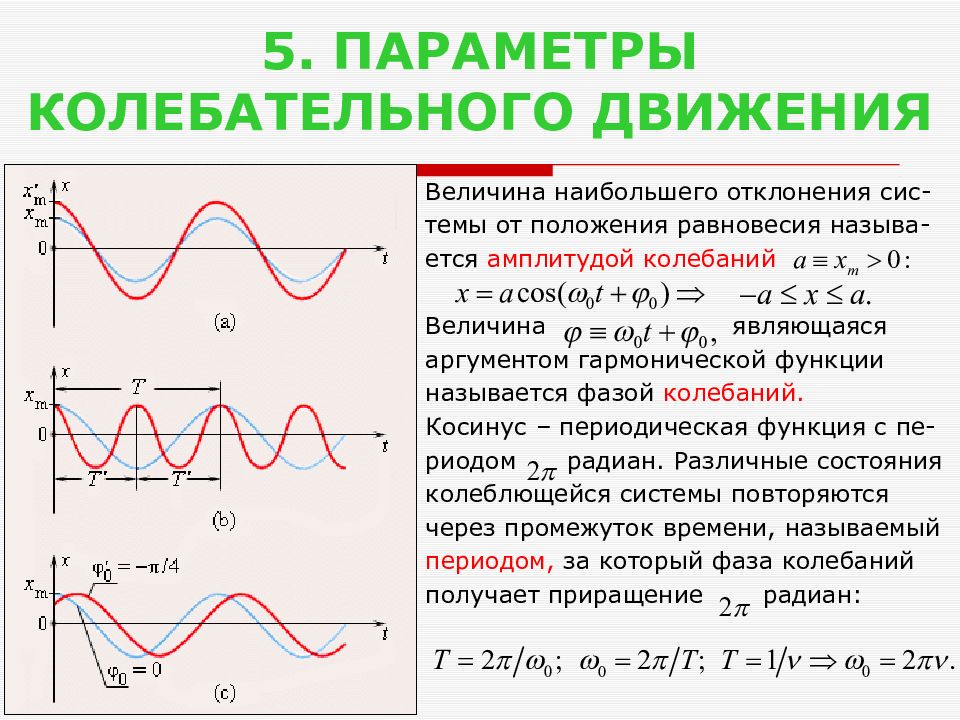
Слайд 6: 5. ПАРАМЕТРЫ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ
Величина наибольшего отклонения сис- темы от положения равновесия называ- ется амплитудой колебаний Величина являющаяся аргументом гармонической функции называется фазой колебаний. Косинус – периодическая функция с пе- риодом радиан. Различные состояния колеблющейся системы повторяются через промежуток времени, называемый периодом, за который фаза колебаний получает приращение радиан:
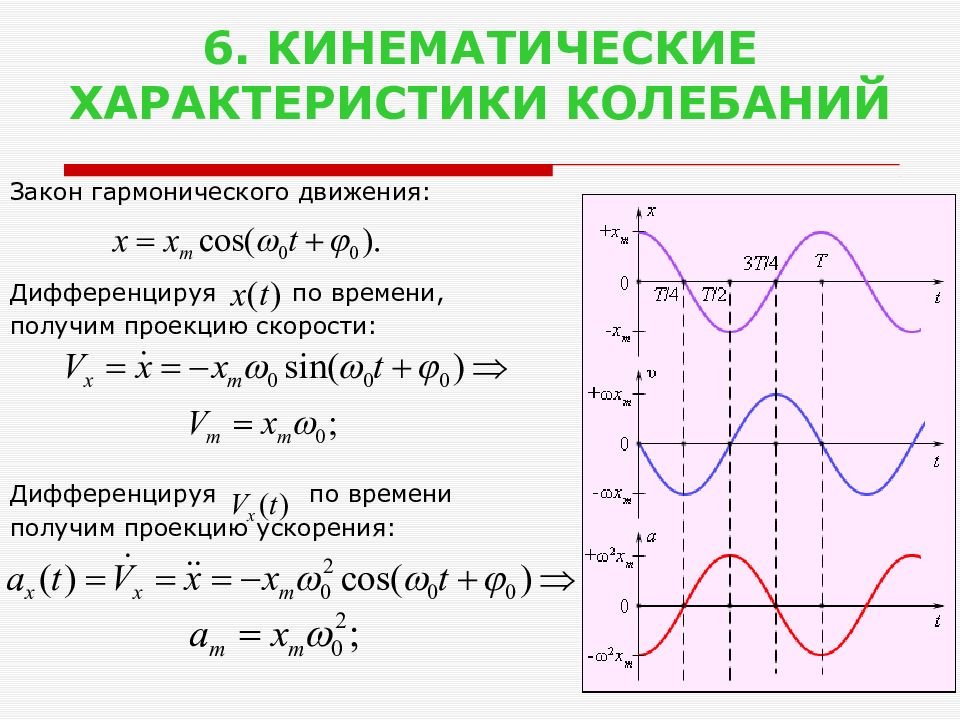
Слайд 7: 6. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОЛЕБАНИЙ
Закон гармонического движения: Дифференцируя по времени, получим проекцию скорости: Дифференцируя по времени получим проекцию ускорения:
Слайд 8: 7. ЭНЕРГИЯ КОЛЕБАНИЙ
Квазиупругая сила является консервативной. Ей отвечает потенциальная энергия полная энергия гармонических колебаний должна оставаться неизменной.
Слайд 9: 8. ПРУЖИННЫЙ МАЯТНИК
Рассмотрим систему, состоящую из тела массой подвешенного на пружине, массой которой можно пренебречь. В положении равновесия сила тяжести уравновешивается упругой силой Будем характеризовать смещение шарика из поло- жения равновесия координатой причем ось направим вертикально вниз, а нуль оси совместим с положением равновесия шарика. Если сместить шарик в положение, характеризуемое координатой то удлинение пружины станет равным а проекция результирующей силы примет значение Маятником называют тело, совершающее колебания под действием силы тяжести.
Слайд 10: 9. МАТЕМАТИЧЕСКИЙ И ФИЗИЧЕСКИЙ МАЯТНИКИ
Физический маятник – любое твердое тело, совершающее малые колебания относительно оси, не проходящей через его центр масс.
Слайд 12: 1 1. УРАВНЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к затуханию колебаний. В простейшем и наиболее часто встречающемся случае сила сопротив - ления пропорциональна скорости :
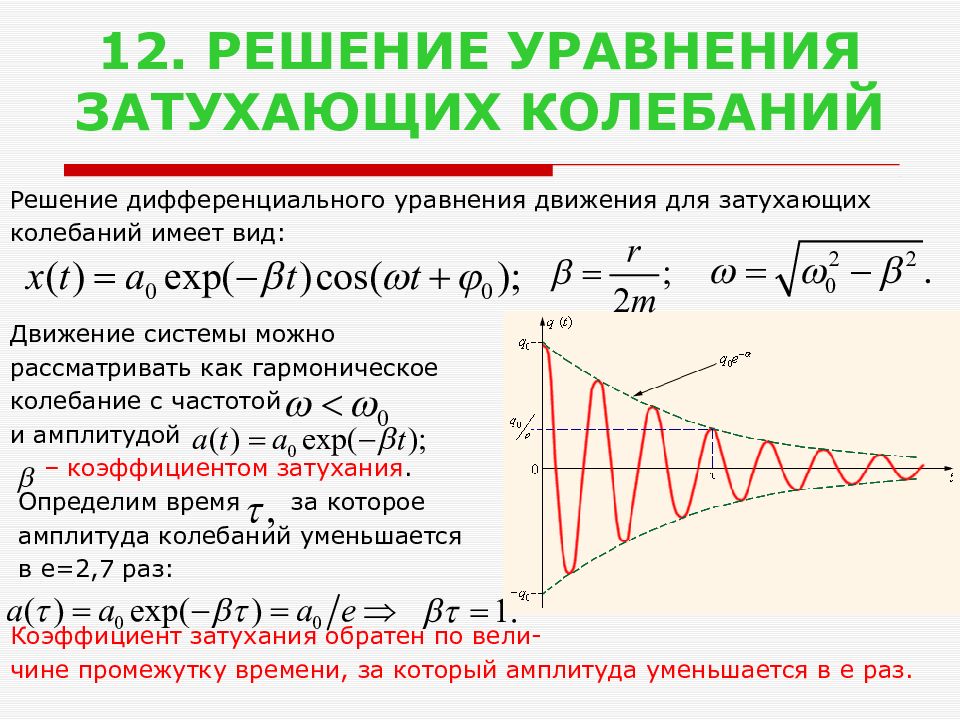
Слайд 13: 12. РЕШЕНИЕ УРАВНЕНИЯ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Решение дифференциального уравнения движения для затухающих колебаний имеет вид: Движение системы можно рассматривать как гармоническое колебание с частотой и амплитудой – коэффициентом затухания. Определим время за которое амплитуда колебаний уменьшается в e =2,7 раз: Коэффициент затухания обратен по вели- чине промежутку времени, за который амплитуда уменьшается в e раз.
Слайд 14: 13. ЛОГАРИФМИЧЕСКИЙ ДЕКРЕМЕНТ ЗАТУХАНИЯ
Отношение амплитуд, соответствующих моментам времени, различающимся на период, называют декрементом затухания Логарифм отношения амплитуд, отстоящих на период, называется логарифмическим декрементом затухания
Слайд 15: 14. ДОБРОТНОСТЬ
Для характеристики потерь энергии в колебательной системе используется величина, называемая добротностью. Добротность в раз превышает число колебаний совершаемых системой за время в течение которого амплитуда колебаний уменьшается в раз.
Слайд 16: 15. ЭНЕРГИЯ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Полная механическая энергия колебательной системы складывается из кинетической и потенциальной энергии, то есть Для затухающих колебаний Скорость изменения энергии системы равна мощности, развиваемой силой сопротивления: В моменты времени, для которых скорость тела равна нулю мощность силы сопротивления также равна нулю. Во все остальные моменты мощность отрицательна и энергия убывает.
Слайд 17: 16. УРАВНЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Рассмотрим движение тела, на которое действуют: возвращающая сила (квазиупругая) сила сопротивления внешняя гармоническая вынуждающая сила с амплитудой Уравнение движения в данном случае будет иметь вид: – амплитуда ускорения и частота внешней вынуждающей силы.
Слайд 18: 17. РЕШЕНИЕ УРАВНЕНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Уравнение движения вынужденных колебаний является неоднородным: Согласно известной математической теореме, общее решение неоднород- ного дифференциального уравнения равно сумме общего решения соот- ветствующего однородного уравнения и частного решения неоднородного уравнения, то есть – частота свободных затухающих колебаний.
Слайд 19: 18. АНАЛИЗ ОБЩЕГО РЕШЕНИЯ
Первое слагаемое описывает собственные затухающие колебания системы. Оно играет заметную роль только в начальной стадии процесса, при установлении колебаний. С течением времени из-за множителя роль первого слагаемого уменьшается и им можно пренебречь, оставляя в решении лишь второе слагаемое. Оно представляет собой гармоническое колебание с частотой внешней вынуждающей силы
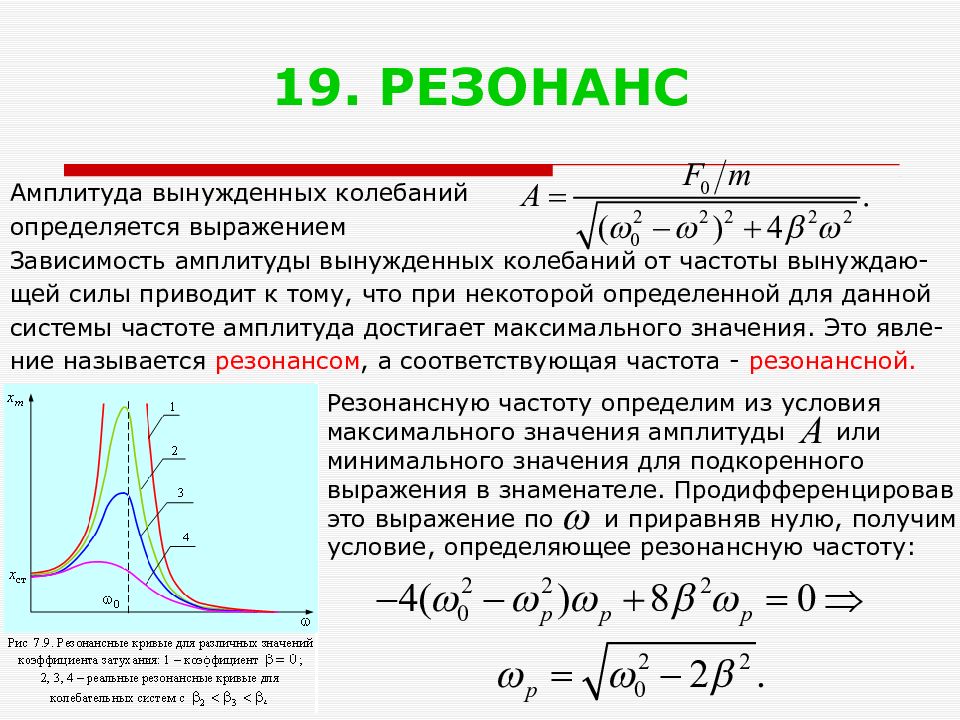
Слайд 20: 19. РЕЗОНАНС
Амплитуда вынужденных колебаний определяется выражением Зависимость амплитуды вынужденных колебаний от частоты вынуждаю- щей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда достигает максимального значения. Это явле- ние называется резонансом, а соответствующая частота - резонансной. Резонансную частоту определим из условия максимального значения амплитуды или минимального значения для подкоренного выражения в знаменателе. Продифференцировав это выражение по и приравняв нулю, получим условие, определяющее резонансную частоту:
Слайд 21: 20. СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ
Пусть частица участвует одновременно в двух взаимно перпендикулярных колебаниях одной частоты. Пусть колебания вдоль оси происходят с нулевой начальной фазой, а вдоль оси со сдвигом по фазе на Тогда уравнения колебаний примут вид: Чтобы получить уравнение траектории в явном виде исключим время Из первого уравнения следует, что Подставляя синус и косинус в формулу для получим: уравнение эллипса. Полуоси этого эллипса в общем случае не совпадают с осями координат.
Слайд 22: 21. ДВИЖЕНИЕ ПО ПРЯМОЙ
Определим форму траектории результирующего колебания для некоторых частных случаев. Пусть В этом случае общее уравнение траектории принимает вид Движение является гармоническим колебанием вдоль прямой с амплитудой 2. Пусть В этом случае Траектория является прямой, лежа- щей во 2-м и 4-м квадрантах.
Слайд 23: 22. ДВИЖЕНИЕ ПО ЭЛЛИПСУ
При общее уравнение траектории принимает вид Это уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. При движение против часовой стрелки. При движение по часовой стрелке
Последний слайд презентации: ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ: 23. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Если то уравнение траектории Знак «+» в выражении для соответствует движению против часовой стрелки, знак «-» – движению по часовой стрелке. принимает вид При равенстве амплитуд эллипс вырождается в окружность. Это означает что равномерное движение по окружности радиуса с угловой скоростью может быть представлена как сумма двух взаимно перпендикулярных колебаний