Вынужденные механические и электромагнитные колебания. Резонанс.
Вынужденные колебания. Колебания, которые происходят под действием периодической вынуждающей силы называются вынужденными колебаниями. Рис. 1 В случае электромагнитных колебаний причиной, вызывающей вынужденные колебания, может быть другое электромагнитной колебание, внешнее по отношению к рассматриваемой системе. Так, например, если колебательный контур включить в цепь переменного тока, то колебания тока и напряжения в этой цепи будут внешними колебаниями по отношению к колебательному контуру. Они вызовут электромагнитные колебания в самом контуре, которые мы и называем вынужденными колебаниями.
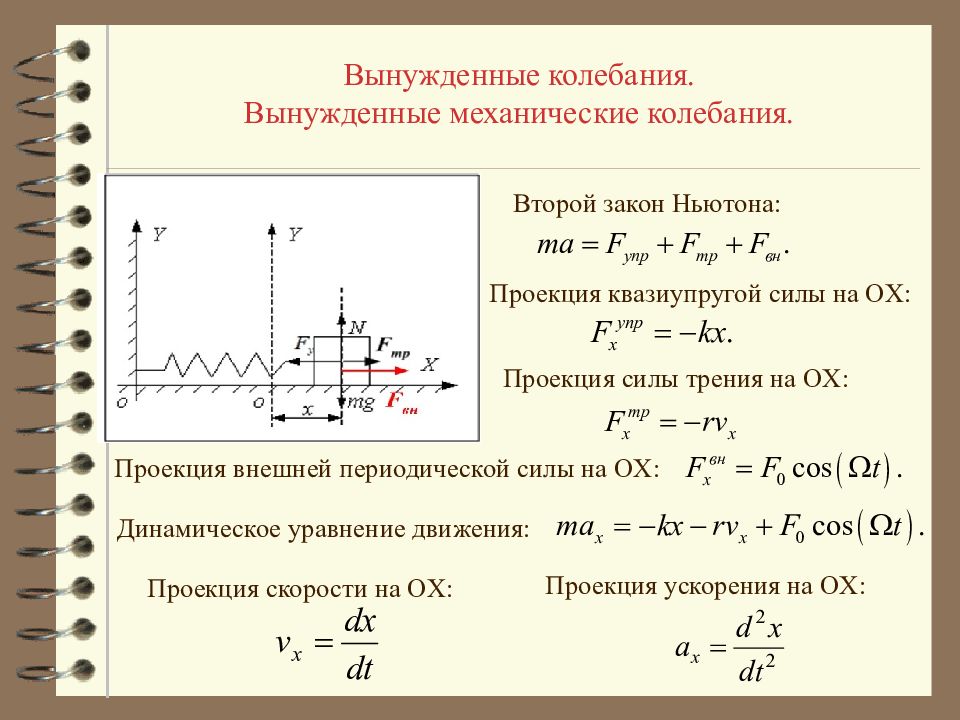
Вынужденные колебания. Вынужденные механические колебания. Второй закон Ньютона: Проекция силы трения на OX : Проекция квазиупругой силы на OX : Проекция скорости на OX : Проекция ускорения на OX : Проекция внешней периодической силы на OX : Динамическое уравнение движения:
Вынужденные колебания. Вынужденные механические колебания. Уравнение движения можно переписать в виде: Разделим уравнение на m : Введем следующие обозначения : 0 – собственная частота незатухающих колебаний без учета трения.
Теперь можно переписать уравнение движения в виде: (1) Мы получили дифференциальное уравнение вынужденных колебаний. Как известно из математики, общее решение неоднородного дифференциального уравнения вида (1) равно сумме общего решения однородного дифференциального уравнения С точки зрения математики это линейное неоднородное дифференциальное уравнение. Приступим к его решению. плюс частное решение неоднородного дифференциального уравнения (1). Вынужденные колебания. Вынужденные механические колебания. ( 2 )
( 2 ) В уравнение (2) подставим функцию и получим характе-ристическое уравнение: - характеристическое уравнение. Решаем линейное однородное уравнение (ещё один раз!): Вынужденные колебания. Общее решение линейного однородного дифференциального уравнения.
Вынужденные колебания. Общее решение линейного однородного дифференциального уравнения. Корни этого характеристического уравнения: Как известно, общим решением дифференциального уравнения второго порядка с постоянными коэффициентами является функция: Подкоренные выражения в формулах, определяющих корни характеристического уравнения, в зависимости от значений параметров и могут быть как положительными, так и отрицательными. Это приводит к тому, что существует два класса решений. Но в этот раз мырассмотрим только колебательное решение.
1. Если 0, то подкоренное выражение будет отрицательным, а корни характеристического уравнения – комплексными. Обозначим тогда Решение уравнения в этом случае будет иметь вид: Или в действительной форме: Здесь A и 0 – произвольные постоянные имеющие смысл амплитуды и начальной фазы колебаний, Вынужденные колебания. Общее решение линейного однородного дифференциального уравнения.
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. Это решение будем искать в виде , Вычислим производные: Нам необходимо найти такие значение параметров B и , при которых (3) будет частным решением уравнения (1). Подставим функцию (3) и найденные значения производных в исходное уравнение (1): ( 1 ) ( 3 )
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. Далее воспользуемся известными из тригонометрии формулами косинуса суммы и синуса суммы двух аргументов: , После очередной группировки слагаемых получим:
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. , Выражения в фигурных скобках обозначим так Отметим, что величины a и b не зависят от времени. Теперь, заменив выражения в фигурных скобках, получим Чтобы функция (3) была частным решением уравнения (1), последнее условие должно выполняться в любой момент времени t. Это возможно лишь в том случае, когда одновременно равны нулю величины a и b.
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. , Из второго уравнения системы Чтобы определить величину B, сначала выразим Sin , через B, , , и . Для этого умножим первое из уравнений системы на sin , а второе – на cos .
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. Сложив уравнения, получим По определению Ранее было получено
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. Подставим значение синуса в первую формулу: Приравняем тангенсы: Откуда
Вынужденные колебания. Частное решение линейного неоднородного дифференциального уравнения. Итак, мы установили, что функция x(t) = Bcos( Ω t + φ ) может быть решением неоднородного дифференциального уравнения (1) только тогда, когда параметры B и определяются формулами
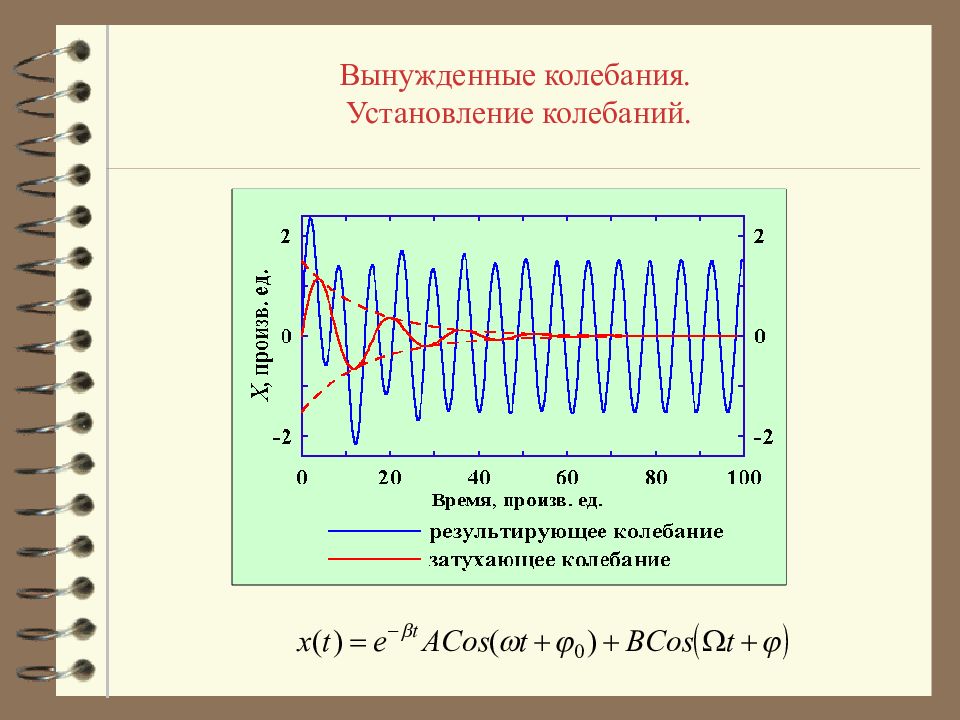
Общее решение неоднородного дифференциального уравнения есть сумма общего решения однородного дифференциального уравнения и частного решения неоднородного уравнения Вынужденные колебания. Общее решение линейного неоднородного дифференциального уравнения. Механические колебания.
Вынужденные колебания. Установление колебаний.
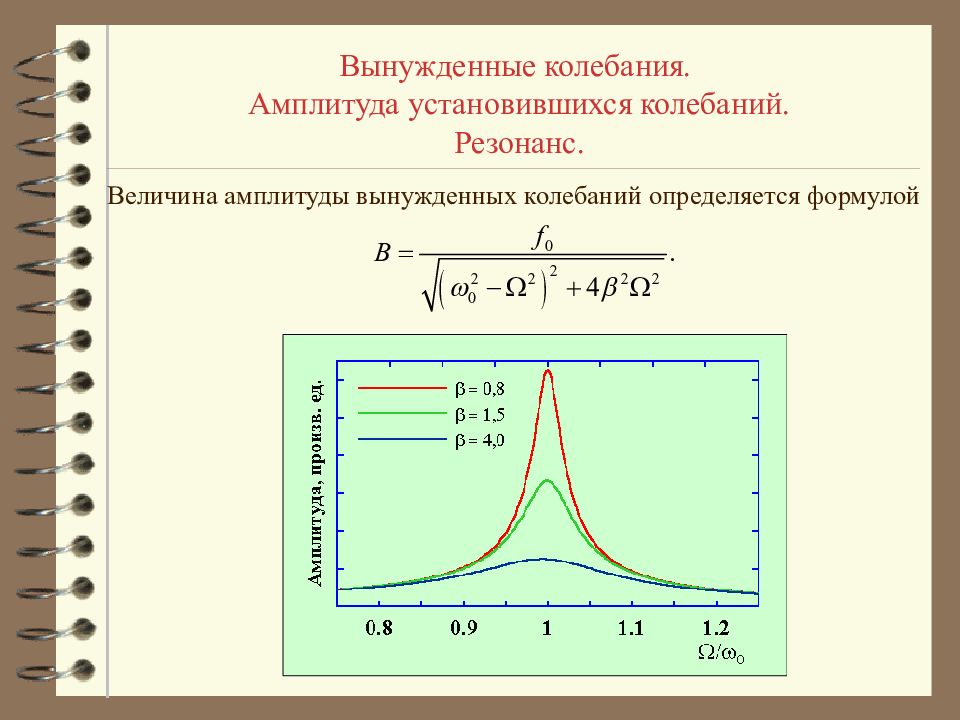
Вынужденные колебания. Амплитуда установившихся колебаний. Резонанс. Величина амплитуды вынужденных колебаний определяется формулой
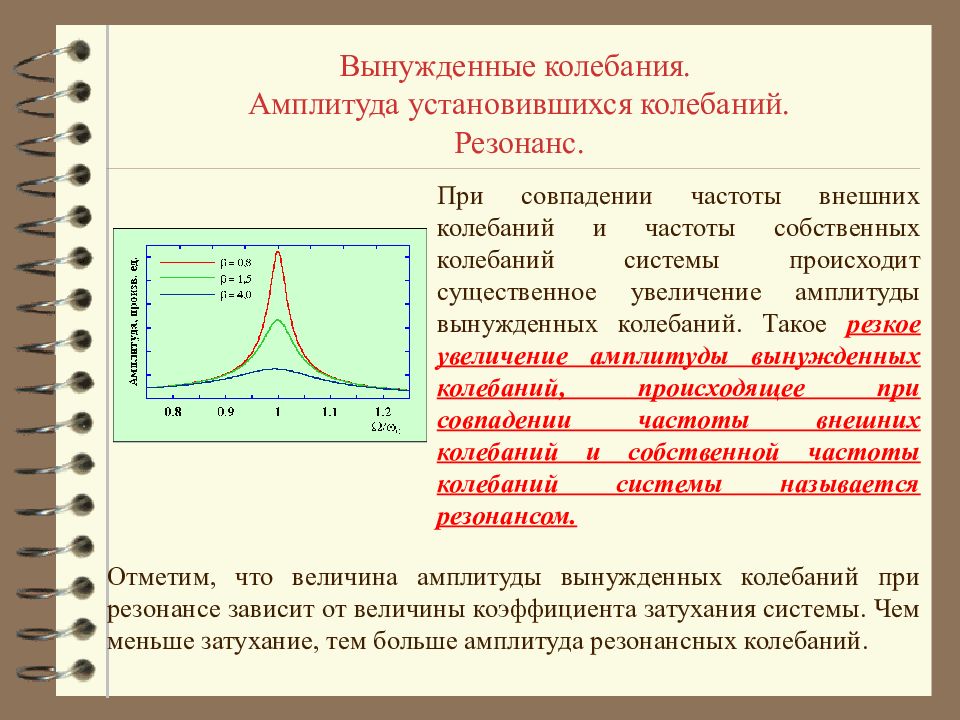
Вынужденные колебания. Амплитуда установившихся колебаний. Резонанс. При совпадении частоты внешних колебаний и частоты собственных колебаний системы происходит существенное увеличение амплитуды вынужденных колебаний. Такое резкое увеличение амплитуды вынужденных колебаний, происходящее при совпадении частоты внешних колебаний и собственной частоты колебаний системы называется резонансом. Отметим, что величина амплитуды вынужденных колебаний при резонансе зависит от величины коэффициента затухания системы. Чем меньше затухание, тем больше амплитуда резонансных колебаний.
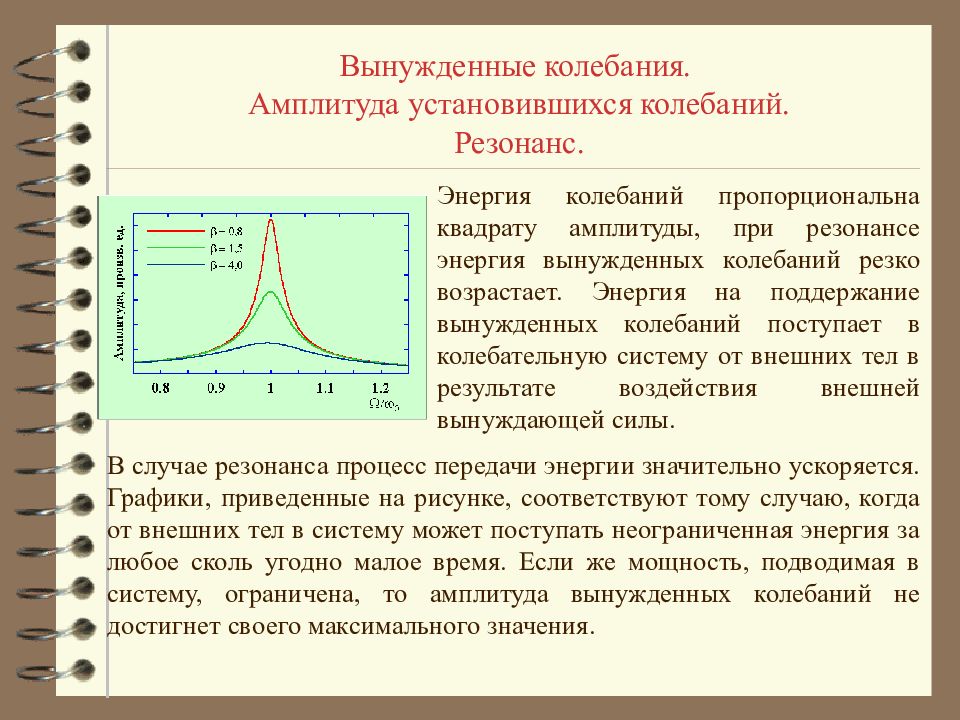
Вынужденные колебания. Амплитуда установившихся колебаний. Резонанс. Энергия колебаний пропорциональна квадрату амплитуды, при резонансе энергия вынужденных колебаний резко возрастает. Энергия на поддержание вынужденных колебаний поступает в колебательную систему от внешних тел в результате воздействия внешней вынуждающей силы. В случае резонанса процесс передачи энергии значительно ускоряется. Графики, приведенные на рисунке, соответствуют тому случаю, когда от внешних тел в систему может поступать неограниченная энергия за любое сколь угодно малое время. Если же мощность, подводимая в систему, ограничена, то амплитуда вынужденных колебаний не достигнет своего максимального значения.
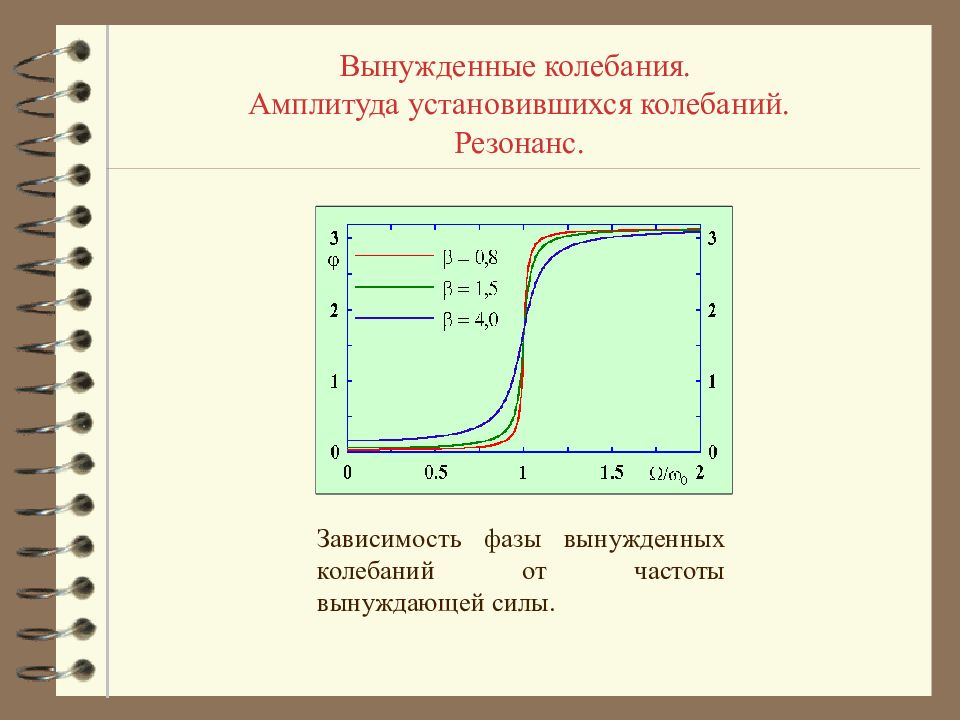
Вынужденные колебания. Амплитуда установившихся колебаний. Резонанс. Зависимость фазы вынужденных колебаний от частоты вынуждающей силы.
Общее решение неоднородного дифференциального уравнения есть сумма общего решения однородного дифференциального уравнения и частного решения неоднородного уравнения Вынужденные колебания. Общее решение линейного неоднородного дифференциального уравнения. Электромагнитные колебания.
