Первый слайд презентации: Глава 8. Элементы комбинаторики (п.п. 39 -43)
Слайд 2: Результаты обучения:
В результате изучения материала главы 8 учащийся должен: уметь методом перебора находить ответы в комбинаторных задачах для небольших объемов перебора; уметь вычислять число упорядоченных пар, пользуясь правилом умножения; уметь вычислять n! ; знать факториалы до 5! и уметь пользоваться таблицей до 10!; уметь находить число перестановок элементов произвольного конечного множества; уметь вычислять, пользуясь формулой ; уметь решать простейшие задачи, в которых число благоприятствующих элементарных событий находится как число сочетаний.
Слайд 3: Теоретический материал
Чтобы найти число комбинаций предметов двух типов, нужно число предметов первого типа умножить на число предметов второго типа. (Комбинаторное правило умножения); Перестановкой из n предметов называется любой способ нумерации этих предметов (способ расположения их в ряд); Число перестановок n предметов равно n! ; Теория вероятностей дает способ нахождения численного значения вероятности события Р(А) = N(A) / N, где N(A) – количество исходов, при которых событие А появляется, N – конечное число равновозможных исходов; Если есть n предметов, то число способов, которыми можно выбрать ровно k из них, называется числом сочетаний из n по k и обозначается и находится по формуле .
Слайд 4: п. 39 задача 4
В автоматических камерах хранения на железнодорожных вокзалах применяется шифр, который состоит из одной буквы и трех цифр, буквы берутся от А до К, исключая Ё и Й, а цифры могут быть любыми от 0 до 9, например Д195, Сколько можно составить различных шифров?
Слайд 5: п.39 задача 4 решение:
Буквы: А, Б, В, Г, Д, Е, Н, З, И, К – 10 букв Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – 10 цифр Д195 10 ∙ 10 ∙ 10 ∙ 10 = 10 000 Ответ: можно составить 10 000 различных шифров.
Слайд 6: п.39 задача 6
Первый класс праздновал Новый год. Каждая девочка подарила каждому мальчику открытку, а каждый мальчик подарил каждой девочке гвоздику. Чего было больше - подаренных открыток или подаренных гвоздик?
Слайд 7: п.39 задача 6 решение:
Каждая девочка подарила каждому мальчику открытку, а каждый мальчик подарил каждой девочке гвоздику. Пример: В классе 13 девочек и 15 мальчиков. подарено открыток 13 ∙ 15 подарено гвоздик 15 ∙ 13 Вывод: Подаренных открыток и подаренных гвоздик было одинаковое количество.
Слайд 8: п.39 задача 7*
Второй класс, в котором 23 ученика, но мальчиков меньше, чем девочек, отправился на экскурсию в музей. За время экскурсии каждый мальчик по одному разу дернул за косичку каждую девочку. Сколько мальчиков и сколько девочек в классе, если всего было произведено 132 дергания за косички?
Слайд 9: п.39 задача 7*решение:
Пусть в классе m мальчиков и n девочек, тогда по комбинаторному правилу умножения число комбинаций – m ∙ n В классе m мальчиков, тогда ( 23 – m) девочек. Произведено m∙ (23 – m ) дерганий за косички, что по условию задачи составляет 132. Составим и решим уравнение: m∙ (23 – m) = 132. Корнями уравнения являются числа 11 и12. По условию задачи мальчиков меньше, чем девочек. Следовательно мальчиков 11, а девочек 12. Ответ: 11 мальчиков и 12 девочек.
Слайд 10: п.39 задача 8*
На приеме в посольстве встретились две делегации, в каждой из которых было несколько дипломатов. Каждый дипломат одной делегации пожал руку каждому дипломату второй делегации. Сколько было членов в каждой делегации, если всего произошло 143 рукопожатия?
Слайд 11: п.39 задача 8* решение:
Пусть в одной делегации m дипломатов, в другой делегации n дипломатов. По комбинаторному правилу умножения количество рукопожатий будет m ∙ n. Всего произошло 143 рукопожатия, следовательно m ∙ n = 143. Проанализируем данное произведение, рассмотрев делители числа 143. Возможны числа 11 и 13. Ответ: в делегациях было 11 и 13 ( или 13 и 11) дипломатов.
Слайд 12: п.40 задача 1
Саша, Ваня и Петя получили номера 1, 2, и 3 для участия в соревнованиях. Запишите в таблицу все возможные способы распределения этих номеров между участниками.
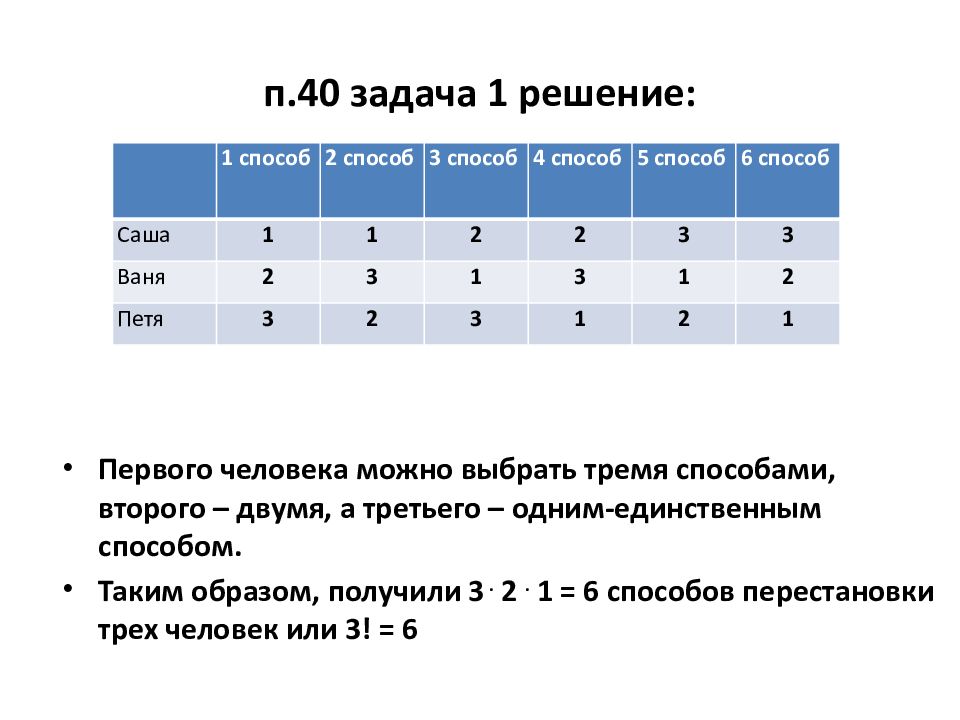
Слайд 13: п.40 задача 1 решение:
1 способ 2 способ 3 способ 4 способ 5 способ 6 способ Саша 1 1 2 2 3 3 Ваня 2 3 1 3 1 2 Петя 3 2 3 1 2 1 Первого человека можно выбрать тремя способами, второго – двумя, а третьего – одним-единственным способом. Таким образом, получили 3. 2. 1 = 6 способов перестановки трех человек или 3! = 6
Слайд 14: Дополнительные задачи:
Сколькими способами 28 учеников можно выстроить в очередь в столовую? Ответ: 28! Решение: 1 способ: Сколько существует способов выстроить в очередь первого ученика (28), второго ученика (27), третьего ученика (26) и т. д. ? По правилу умножения получаем 28 ∙ 27 ∙ 26 ∙ 25 ∙ … ∙ 1 = 28! 2 способ: число перестановок 28! Важно помнить, что задачу можно решить не только по формуле, но и воспользовавшись рассуждениями.
Слайд 15: Дополнительные задачи
Ребята Андрей, Боря, Витя, Гриша, Дима и Женя решили покататься на карусели. На ней шесть сидений. Одно изображало льва, другое тигра, третье слона, четвертое оленя, пятое медведя и шестое жирафа. Ребята заспорили, кому куда садиться, поэтому решили перепробовать все способы. Сколько раз пришлось им прокатиться на карусели? (6! = 720) Посчитайте приблизительно сколько времени займет катание на карусели. В семье шесть человек, а за столом на кухне шесть стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти шесть стульев по-новому. Сколько дней члены семьи смогут осуществлять задуманное? (6! = 720 дней, почти два года)
Слайд 16: Дополнительные задачи
Проказница Мартышка, Осёл, Козел да Косолапый Мишка задумали сыграть квартет. Стой, братцы, стой! – кричит Мартышка, - погодите! Как музыке идти! Ведь Вы не так сидите. И так, и этак пересаживались – опять музыка не идет на лад. Тут пуще прежнего пошли у них раздоры, кому и как сидеть. Сколько существует способов рассадить музыкантов ? (4! =24) В 8 классе в среду 7 уроков: алгебра, геометрия, литература, физкультура, русский язык, биология, английский язык. а) Сколько можно составить различных вариантов расписания на среду ? (7! = 5040) б) В скольких вариантах расписания физкультура будет значиться последним уроком? (6! = 720)
Слайд 17: п.41 задача 1
Найдите вероятность того, что трехзначный номер случайно проезжающей мимо машины состоит из цифр 0, 4, 5 в произвольном порядке.
Слайд 18: п.41 задача 1решение:
Общее число равновозможных исходов N = 10∙ 10∙ 10 = 1000; Событие А «трехзначный номер случайно проезжающей мимо машины состоит из цифр 0, 4, 5 в произвольном порядке» Число благоприятствующих событий, при которых событие А появляется N(A) = 3! = 6; Вероятность события А Р(А) = 6⁄1000 = 0,006 Ответ: Р(А) = 0,006
Слайд 19: п. 41 задача 3
Какова вероятность того, что среди последних четырех цифр случайного телефонного номера : а) встретится цифра 7; б) встретится цифра 2 или цифра 3.
Слайд 20: п.41 задача 3 решение:
а) N = 10 ∙ 10 ∙ 10 ∙10 = 10000 Событие ͞ А – «не встретится цифра 7» N(͞ А ) = 9 ∙ 9 ∙ 9. 9 = 6561; Р(͞А) = 6561/ 10000 = 0,6561; Р(А) = 1 – Р( Ā ); Р(А) = 1 – 0,6561 = 0,3439. Ответ: Р(А) = 0,3439.
Слайд 21: п. 41 задача 3 решение:
б) N = 10 ∙ 10 ∙ 10 ∙10 = 10000 Событие ͞А – « не встретятся цифры 2 и 3» N( ͞А) = 8 ∙ 8 ∙ 8. 8 = 4096; Р(͞А) = 4096/10000 = 0,4096; Р(А) = 1 – Р(͞А); Р(А) = 1 – 0,4096 = 0,5904; Ответ: Р(А) = 0, 5904.
Слайд 22: п.41 задача 5
На полке у Миши 6 видеокассет. На дне рождения Миша снял все кассеты с полки. Часть фильмов ребята посмотрели вместе, а когда гости ушли, Миша поставил все кассеты снова на полку в случайном порядке. Найдите вероятность того, что кассеты оказались в том же порядке, что были прежде.
Слайд 23: п. 41 задача 5 решение:
N = 6! = 720 N(A) = 1 Р(А) = 1/720 ≈ 0,0014 Ответ: Р(А) ≈ 0,0014
Слайд 24: П.41 задача 9
Слово «апельсин» написали на полоске картона и разрезали полоску на буквы. Девочка, играя, выложила их в ряд в случайном порядке. Найдите вероятность того, что это слово «спаниель».
Слайд 25: п. 41 задача 9 решение:
N = 8! = 40320 N( А) = 1 Р(А) = 1/40320 ≈ 0,000025 Ответ: Р(А) ≈ 0,000025
Слайд 26: п.42 задача 11, п. 43 задача 5
На билете лотереи «Честная игра» имеется 20 закрытых букв, ровно 10 из них – буквы слова «АВТОМОБИЛЬ». Буквы разбросаны случайным образом. По правилам лотереи, если владелец билета, открыв ровно 10 букв, откроет все буквы слова «АВТОМОБИЛЬ», то он выигрывает автомашину. а) Сколько существует способов открыть 10 букв? б) Сколько существует способов открыть 10 букв так, чтобы выиграть автомобиль? Найдите вероятность, открыв случайным образом 10 букв, открыть все буквы слова «автомобиль»
Слайд 27: Решение:
а) = 184756 ; N =184756 б) Событие А « открыв случайным образом все 10 букв, открыть слово « автомобиль» N(A) = 1 Р(А) = 1 / 184756 Ответ: Р(А) = 1/184756
Слайд 28: п. 43 задача 1
Для участия в телевикторине случайным образом выбирают 3 игроков из 8 претендентов. Какова вероятность того, что будут выбраны 1-ый, 4-ый и 8-ой игроки?
Слайд 29: Решение:
N =56 Событие А « будут выбраны 1-ый, 4-ый и 8-ой игроки» N (A) = 1 Р (А) = 1/56 = 0,018 Ответ: Р(А) = 0,018
Слайд 30: п. 43 задача 6 (в, г)
Найдите вероятность того, что все буквы «о» окажутся на своих местах, если случайным образом перемешать и выстроить в ряд все буквы слова в) «околоток» г) «обороноспособность»
Слайд 31: п. 43 задача 6(в, г) решение:
в) «околоток» N = N(A) = 1 P(A) = 1 /70 =0,014 г) « обороноспособность» N = N(A) = 1 Р(А) = 1/31824 = 0, 000031
Слайд 32: п. 43 задача 10*
В магазин привезли 10 синих и 10 коричневых костюмов. Продавщица случайным образом выбирает 8 из них, чтобы выставить на витрине. Найдите вероятность того, что будет отобрано 3 синих и 5 коричневых костюмов.
Слайд 34: п. 43 задача 12*
Иван Иванович купил билет лотереи «Спортлото 5 из 36». На билете изображены 36 номеров от 1 до 36. нужно вычеркнуть ровно 5 из них. При розыгрыше случайным образом выбираются 5 выигрышных номеров. Какова вероятность того, что Иван Иванович, зачеркнув 5 чисел, угадает: а) ровно 5 выигрышных номеров; б) ровно 4 выигрышных номера.