Для хранения растрового изображения нужно выделить в памяти V = K · i бит, где K – количество пикселей i – глубина цвета (разрядность кодирования) количество пикселей изображения K вычисляется как произведение ширины рисунка на высоту (в пикселях) K= B*H глубина кодирования – это количество бит, которые выделяются на хранение цвета одного пикселя i = log 2 K
Код Цвет 00 red 01 green 10 blue 11 white Псевдопример 2-битной палитры
Тип №1. Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов. Решение. Используем формулу V = K * i Количество пикселей- K = 160*160= 2 3 *20*2 3 *20=400*2 6 = 25*2 1 0 Глубина цвета (количество бит на пиксель) i = log 2 N= log 2 256 = 8 N=2 i, где N=256 Объём памяти V= 25*2 1 0 * 8 =25 * 2 1 0 *2 3 = 25 * 2 1 0 *2 3 / 2 13 = 25 Кбайт
Тип №2 Рисунок размером 32 на 64 пикселя занимает в памяти 512 байт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения. Решение. Количество пикселей- K = B*H = 32*64 = 2048 Глубина цвета (количество бит на пиксель) - i = V/ B*H = 512*8 = 4096 бит/2048 =2 бита Количество цветов в палитре – N= 2 i = 2 2 = 4 цвета
Тип №3 После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Сколько Кбайт занимал исходный файл ? Решение. По формуле объема файла изображения имеем: V = K *i, где K — общее количество пикселей, i — глубина цвета (количество бит, выделенное на 1 пиксель) i можно найти, зная количество цветов палитры: кол-во цветов N = 2 i : до преобразования: i = 8 ( N = 2 8 = 256) после преобразования: i = 2 ( N = 2 2 = 4)
Выразим x в первом уравнении: x=V/8 Подставим во второе уравнение и найдем V (объем файла): V-18 = V/4 4V-V = 72 3V = 72 V = 24 Ответ: 24 Кбт Составим систему уравнений на основе имеющихся сведений, примем за x количество пикселей: V = x*8 (V-18) после = x*2 Решение.
После преобразования растрового графического файла его объем уменьшился в 2 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 16-цветной палитре? k- количество точек (оно не изменится) Из условия задачи: k*x/2= k*4, (сокращаем на k, т.к. это константа) x/2= 4, x = 8 бит 2 8 =256 цветов в палитре до преобразования изображения Ответ: 256 цветов Тип №3
В процессе преобразования растрового графического изображения количество цветов уменьшилось с 512 до 8. Во сколько раз уменьшился информационный объём файла? Решение. По формуле количества цветов N = 2 i Для кодирования 512 цветов необходимо 9 бит. 512 = 2 9 Для кодирования 8 цветов необходимо 3 бита. 8 = 2 3 Таким образом, количество бит для кодирования каждого пикселя уменьшилось в 3 раза (9 и 3). Следовательно, объём файла уменьшится в 3 раза, т.к. V и i находятся в прямой зависимости. Ответ: в 3 раза Тип №3
Тип №4 Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер исходного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.
Решение. По формуле объема файла изображения имеем: V = K *i, где K — общее количество пикселей или разрешение, i — глубина цвета (количество бит, выделенное на 1 пиксель) Но разрешение на самом деле имеет два сомножителя ( пикселей по ширине * пикселей по высоте ). Поэтому при уменьшении разрешения в два раза, уменьшаются оба числа, т.е. K уменьшится в 4 раза вместо двух.
Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после: 42 = K*i V = K/4 * 4*i или 42 = K*i V = K * i Выразим K в первом уравнении: K = 42/i Подставим во второе уравнение и найдем V (объем файла): V = (42/i) * i V = 42 Ответ: 42
Тип №5 Сканируется изображение размером 10х10 см. Разрешающая способность сканера 600 dpi. Глубина цвета составляет 32 бита. Чему равен объём файла в Мбайтах? 600 dpi – это 600 точек на дюйм. 1 дюйм =2,5 см Переводим 600 dpi в точки на см 600 : 2,5= 240 точек на см Изображение 10х10 = 240*10*240*10=5760000 точек всего 240=24*10=3*2 3 *2*5=3*2 4 *5 240*10=3*2 5 *5 2 240*10*240*10=3*2 10 *5 4 Объём файла = 32 * 5760000 = 2 5 *2 10 *9*5 4 = 2 15 *5 4 *9 бит /2 13 = = 4*625*9 Кбайт= 22500 Кбайт/1024= 21,97 Мбайт Решение. Способ №1
Прежде всего, переведем сантиметры в дюймы. 1 дюйм =2,54 см 10/2,54 = 4 дюйма (приблизительно). Т.е. изображение - 4х4 дюйма. Значит, с учетом разрешающей способности сканера изображение разобьется на 4х4х600х600 пикселей. 4 = 2 2 600=6*100=2*3*4*25= 2 3 *3*5 2 4х4х600х600= 2 10 *9*5 4 1 пиксель кодируется 32 битами. Отсюда все изображение закодируется 32х16х600х600= 21,97Мб 22Мб (приблизительно) Способ №2
Определить информационный объём фотографии (10 х 15) см отсканированной с разрешением 300 ppi с использованием палитры в 256 цветов. К- разрешение( количество пикселей) i – глубина цвета ppi – разрешение сканера Решение. Объём отсканированного изображения: V= K * ppi 2 * i
Решение. Переводим размер изображения в дюймы 10/2,5=4 дюйма; 15/2,5=6 дюймов, т.е. изображение (10 х 15) см= (4 х 6) дюймов i = 8 бит V= 4*6*300*300*8=2,05 Мб Ответ: 2 Мбт
Для хранения в информационной системе документы сканируются с разрешением 800 ppi и цветовой системой, содержащей 2 16 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 16 Мбайт. В целях экономии было решено перейти на разрешение 400 ppi и цветовую систему, содержащую 2 12 = 4 096 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Условие
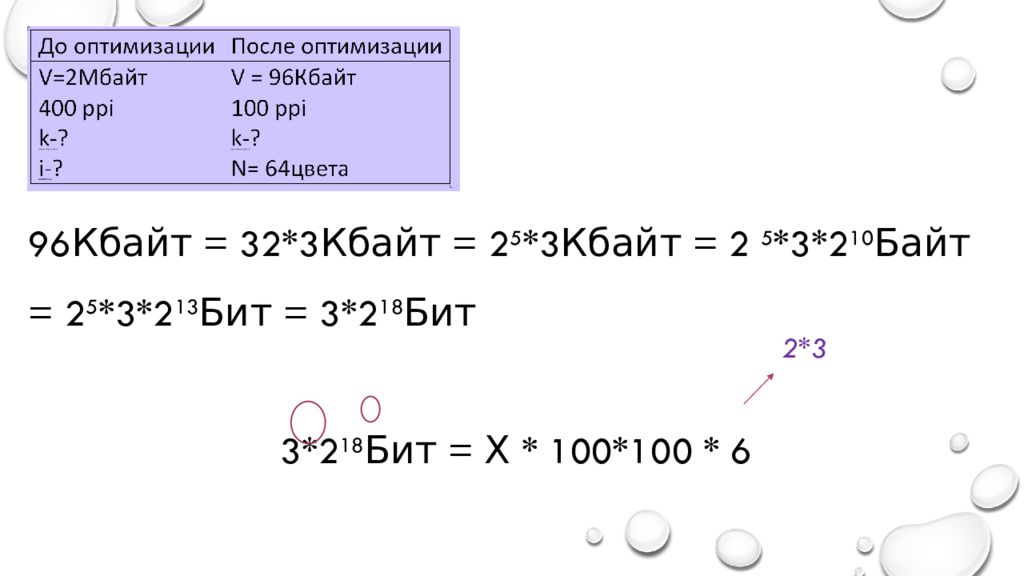
Для хранения в информационной системе документы сканируются с разрешением 400 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 2 Мбайта. В целях экономии было решено перейти на разрешение 100 ppi и цветовую систему, содержащую 64 цвета. Средний размер документа, отсканированного с изменёнными параметрами, составляет 96 Кбайт. Определите количество цветов в палитре до оптимизации.
9 6Кбайт = 32*3Кбайт = 2 5 *3Кбайт = 2 5 *3*2 10 Байт = 2 5 *3*2 13 Бит = 3*2 18 Бит 3*2 18 Бит = Х * 100*100 * 6 2*3
Решение. Ответ: 256
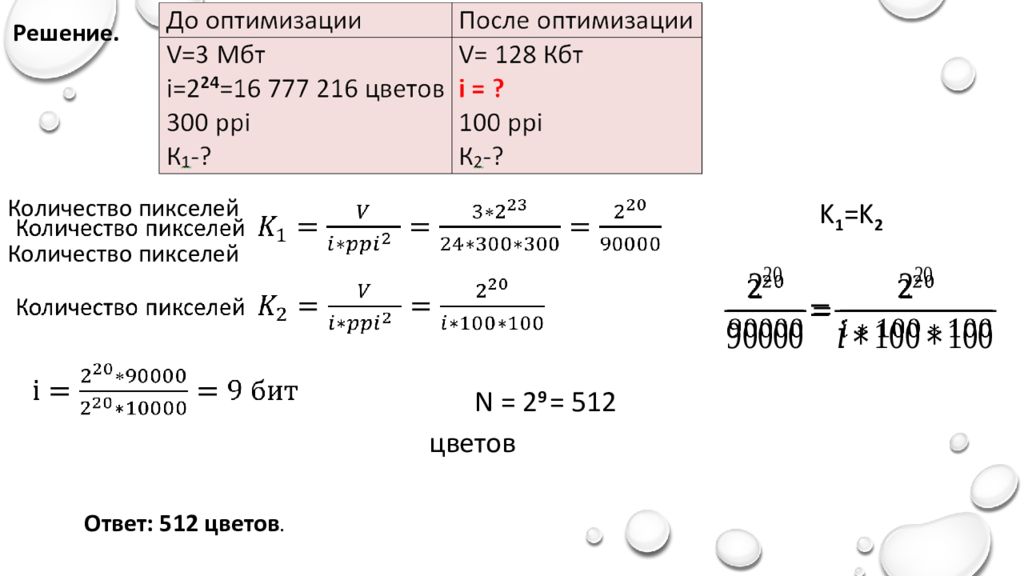
Для хранения в информационной системе документы сканируются с разрешением 300 ppi и цветовой системой, содержащей 2 24 = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 3 Мбайт. В целях экономии было решено перейти на разрешение 100 ppi и цветовую систему с уменьшенным количеством цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 128 Кбайт. Определите количество цветов в палитре после оптимизации.
Решение. Количество пикселей Количество пикселей K 1 =K 2 N = 2 9 = 512 цветов Ответ: 512 цветов.
Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2 24 = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 16 Мбайт. В целях экономии было решено перейти на разрешение 300 ppi и цветовую систему, содержащую 64 цвета. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами? Автоматическая камера производит растровые изображения размером 200×256 пикселей. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Объём файла с изображением не может превышать 65 Кбайт без учёта размера заголовка файла. Какое максимальное количество цветов можно использовать в палитре? Самостоятельно
Камера делает фотоснимки размером 1600 1200 пикселей. На хранение одного кадра отводится 1 Мбайт. Найдите максимально возможное количество цветов в палитре изображения. Цвет пикселя определяется тремя составляющими: голубой, пурпурный и жёлтый. Под каждую составляющую одного пикселя отвели по 4 бита. В какое количество цветов можно раскрасить пиксель? После преобразования растрового 256-цветного графического файла в 16-цветный формат его размер уменьшился на 15 Кбайт. Сколько Кбайт составил исходный файл?
Для хранения в информационной системе документы сканируются с разрешением 200 ppi и цветовой системой, содержащей 256 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 3 Мбайт. Для повышения качества было решено перейти на разрешение 600 ppi и цветовую систему, содержащую 2 24 = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами? Чему равна минимальная ширина квадратной картинки, если её объём 1 Кбт, а палитра содержит 256 цветов.
Ответы: №1-1 Мб №2 – 1024 №3 – 16 №4 Решение. На весь пиксель необходимо i =4*3=12 бит. Количество цветов K= 2 i = 2 12 = 4096 цветов №5-30 Кбт №6- 81Мбт №7-32
В информационной системе хранятся изображения размером 2048 × 1600 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 8 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 64 Кбайт. Для хранения 32 изображений выделено 12 Мбайт памяти. Какое максимальное количество цветов можно использовать в палитре каждого изображения?
Решение.
№1. В информационной системе хранятся изображения размером 1600 × 1200 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 5 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 100 Кбайт. Для хранения 32 изображений выделено 10 Мбайт памяти. Какое максимальное количество цветов можно использовать в палитре каждого изображения? №2. В информационной системе хранятся изображения размером 1024 × 768 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 6 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 54 Кбайт. Для хранения 32 изображений выделено 6 Мбайт памяти. Какое максимальное количество цветов можно использовать в палитре каждого изображения? Самостоятельно
Ответы: №1 -16 №2 -256
