Первый слайд презентации: Координаты вектора
Пусть на плоскости задана прямоугольная система координат. Определим понятие координат вектора. Для этого отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим векторы с координатами (1, 0), (0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем рисовать эти векторы, отложенными от начала координат и называть их координатными векторами.
Слайд 2: Теорема
Теорема. Вектор имеет координаты ( x, y ) тогда и только тогда, когда он представим в виде Доказательство. Отложим вектор от начала координат, и его конец обозначим через А. Имеет место равенство Точка А имеет координаты ( x, y ) тогда и только тогда, когда выполняются равенства и, значит,
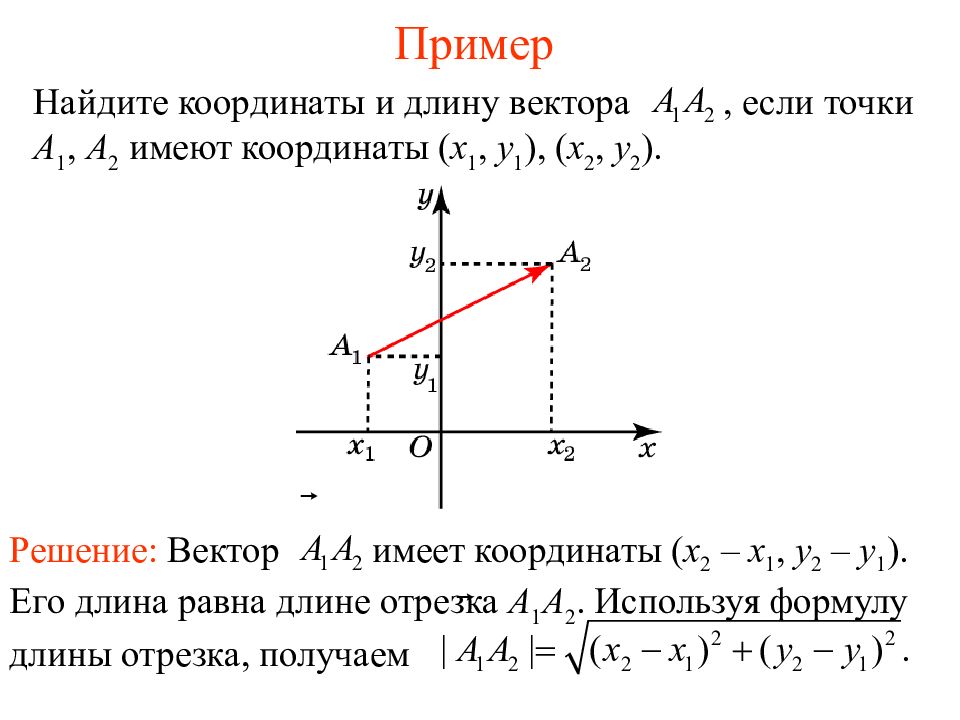
Слайд 3: Пример
Найди те координаты и длину вектора, если точки А 1, А 2 имеют координаты ( x 1, y 1 ), ( x 2, y 2 ). Решение: В ектор имеет координаты ( x 2 – x 1, y 2 – y 1 ). Его длина равна длине отрезка А 1 А 2. Используя формулу длины отрезка, получаем
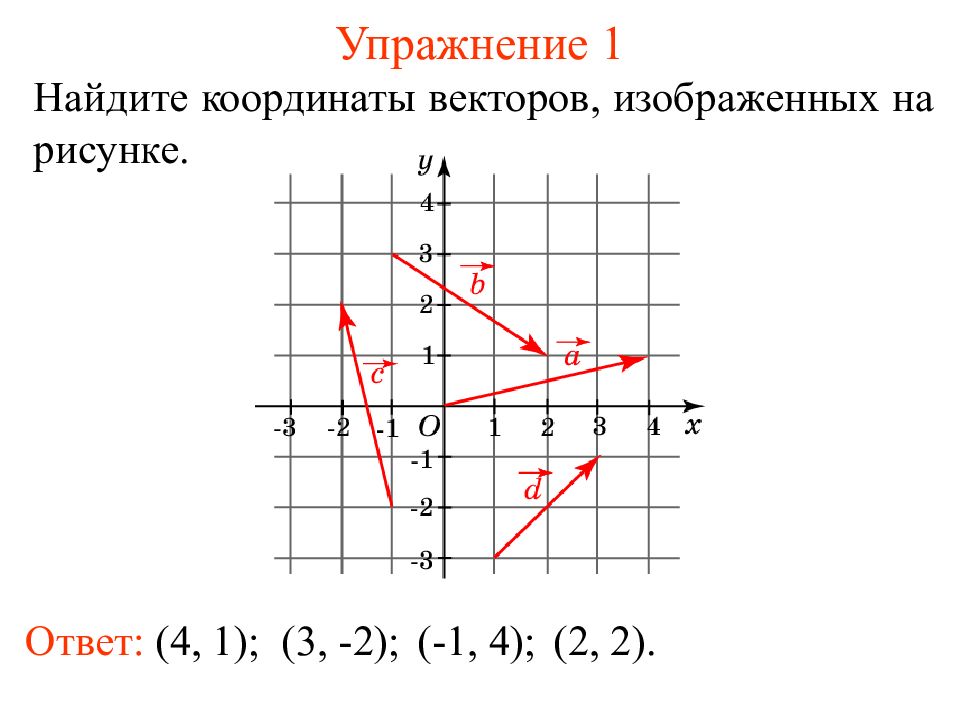
Слайд 4: Упражнение 1
Ответ: ( 4, 1 ); На йдите координаты векторов, изображенных на рисунке. ( 3, -2 ); ( -1, 4 ); ( 2, 2 ).
Слайд 5: Упражнение 2
Ответ: а) (–2, 6); Назовите координаты векторов: а) б) в) г) б) (1, 3); в) (0, -3); г) (-5, 0).
Слайд 6: Упражнение 3
Ответ: (5, -2). Найдите координаты вектора, если точки A 1, A 2 имеют координаты (-3, 5), (2, 3) соответственно.
Слайд 7: Упражнение 4
Выразите длину вектора через его координаты ( x, y ). Ответ:
Слайд 8: Упражнение 5
Ответ: (5, -6). Найдите координаты точки N, если вектор имеет координаты (4, -3) и точка M – (1, -3).
Слайд 9: Упражнение 6
Ответ: а) (-7, 9); Найдите координаты вектора, если: а) A (2, -6), B (-5, 3); б) A (1, 3), B (6, -5); в) A (-3, 1), B (5, 1). б) (5, -8); в) (8, 0).
Слайд 10: Упражнение 7
Ответ: (- a, - b ). Вектор имеет координаты ( a, b ). Найдите координаты вектора.
Слайд 11: Упражнение 8
Ответ: (-2, 0). Даны три точки А (1, 1), В (-1, 0), С (0, 1). Найдите такую точку D ( x, y ), чтобы векторы и были равны.
Слайд 12: Упражнение 9
Ответ: (1, 3) и (1, -3). Найдите координаты векторов и, если (1, 0), (0, 3).
Слайд 13: Упражнение 10
Ответ: а) (1, -2); Даны векторы (-1, 2) и (2, -4). Найдите координаты вектора: а) б) в) б) (-1, 2); в) (11, -22).
Последний слайд презентации: Координаты вектора: Упражнение 1 1
Вершины треугольника имеют координаты A (1, 3 ), B (2, 1) и C (3, 4). Найдите координаты точки M пересечения медиан. Решение: Следовательно, имеет координаты Точка M имеет координаты