Положение плоскости в пространстве можно определить, задав какую-либо точку М 0 на плоскости и какой-либо нормальный вектор. Нормальным вектором плоскости называется любой вектор, перпендикулярный к этой плоскости.
Слайд 3
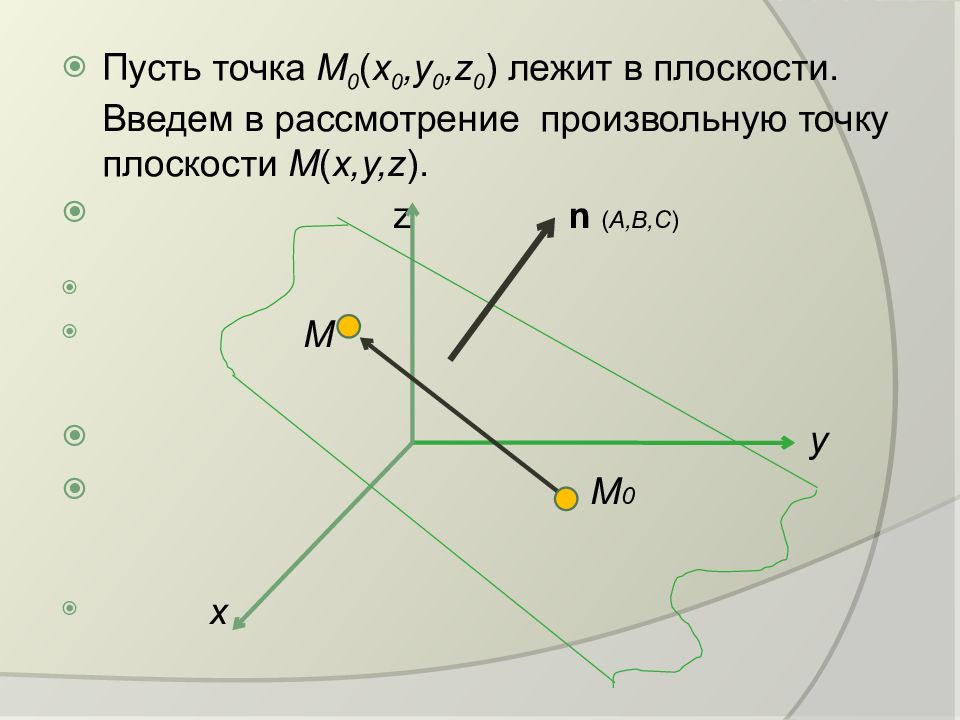
Пусть точка М 0 ( х 0,у 0, z 0 ) лежит в плоскости. Введем в рассмотрение произвольную точку плоскости М ( х,у, z ). z n ( A,B,C ) M y M 0 x
Слайд 4
Векторы и ортогональны. A ( x-x 0 )+ B ( y-y 0 )+ C ( z-z 0 )=0 Уравнение плоскости по точке и нормальному вектору.
Слайд 5
Пример 1 : Написать уравнение плоскости, проходящей через точку М(2,3,-1) перпендикулярно вектору Решение : По формуле : 1( х -2)+2( у -3)-3( z +1)=0 или х +2 у -3 z -11=0
Слайд 6
Пример 2 : Написать уравнение плоскости, проходящей через точку М(1,0,0) перпендикулярно вектору. Решение : Получаем: 2( х -1)+0( у -0)+1( z - 0)=0 или 2 х + z -2=0.
Слайд 7: Общее уравнение плоскости
A ( x - x 0 )+ B ( y - y 0 )+ C ( z - z 0 )=0, раскроем в нем скобки и обозначим – A х 0 -Ву 0 -С z 0 = D. Приведем уравнение рассматриваемой плоскости к виду: Ax+By+Cz+D =0 - - общее уравнение плоскости. Коэффициенты А,В,С являются координатами нормального вектора плоскости.
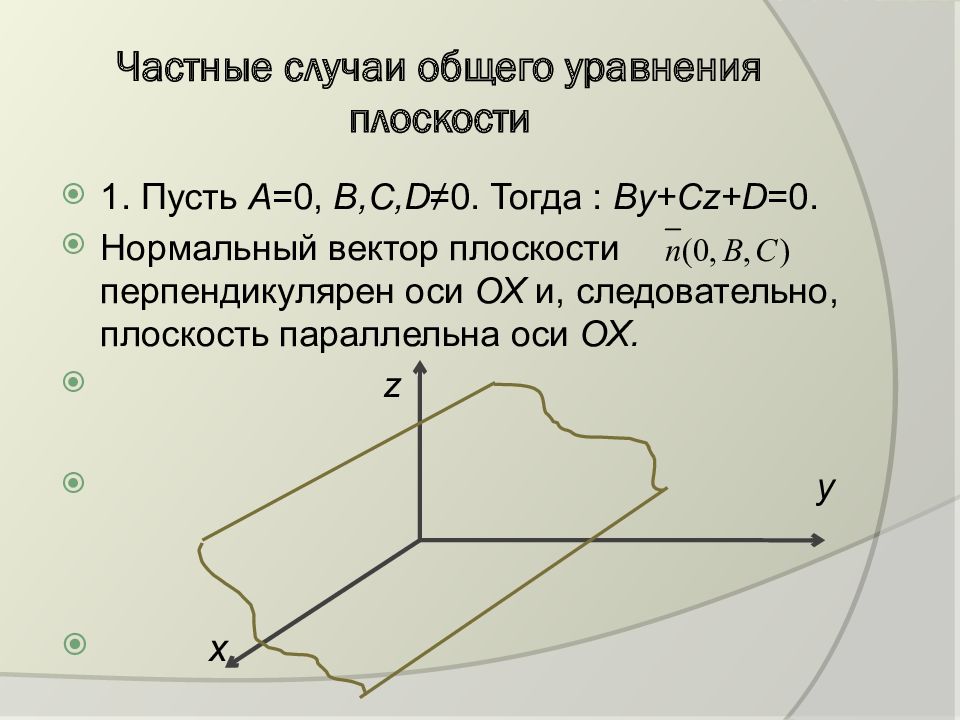
1. Пусть А =0, В,С, D ≠0. Тогда : By + Cz + D =0. Нормальный вектор плоскости перпендикулярен оси ОХ и, следовательно, плоскость параллельна оси ОХ. z y x
Слайд 9
Уравнения Ax + Cz + D =0 и Ax + By + D =0 выражают плоскости, параллельные осям ОУ и OZ. 2. D = 0, А,В,С ≠ 0. Уравнение плоскости: Ax + By + Cz =0. Точка О ( 0,0,0 ) удовлетворяет уравнению плоскости. Уравнение задает плоскость, проходящую через начало координат. 3. А = 0, D = 0, В,С ≠ 0. Уравнение плоскости: By + Cz = 0. Плоскость одновременно параллельна оси ОХ и проходит через начало координат, т.е. проходит через ось ОХ.
Слайд 10
Аналогично уравнения Ax + Cz =0 и Ax + By =0 выражают плоскости, проходящие через оси OY и OZ. 4. А =0, В =0, С, D ≠0. Уравнение плоскости: Cz + D =0. Плоскость одновременно параллельна осям ОХ и ОУ, т.е. координатной плоскости ОХУ. Аналогично уравнения By + D =0, и Ax + D =0 выражают плоскости, параллельные координатным плоскостям OXZ и OYZ.
Слайд 12
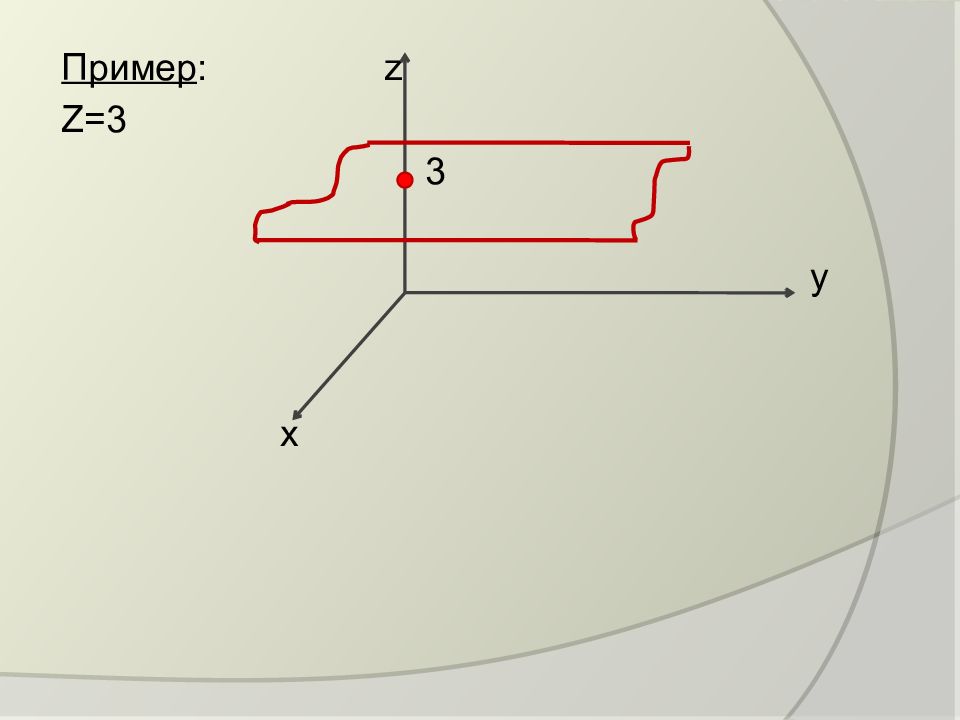
А =0, В =0, D =0, С ≠0. Уравнение плоскости: Cz =0 или z =0. Это плоскость одновременно параллельная координатной плоскости ОХУ, т.е. сама координатная плоскость ОХУ. Аналогично: у =0 и х =0 – уравнения координатных плоскостей OXZ и OYZ.
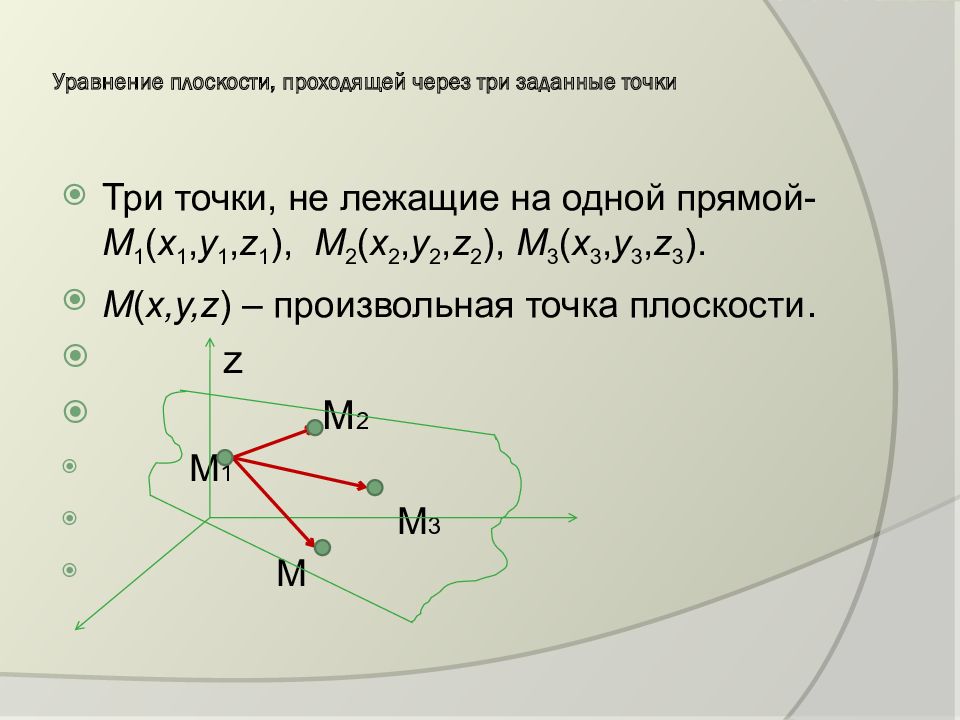
Три точки, не лежащие на одной прямой- M 1 ( x 1, y 1, z 1 ), M 2 ( x 2, y 2, z 2 ), M 3 ( x 3, y 3, z 3 ). M ( x, y, z ) – произвольная точка плоскости. z M 2 М 1 М 3 М
Слайд 14
Векторы компланарны. Их смешанное произведение равно нулю. Это искомое уравнение плоскости, проходящей через три заданные точки.
Слайд 15
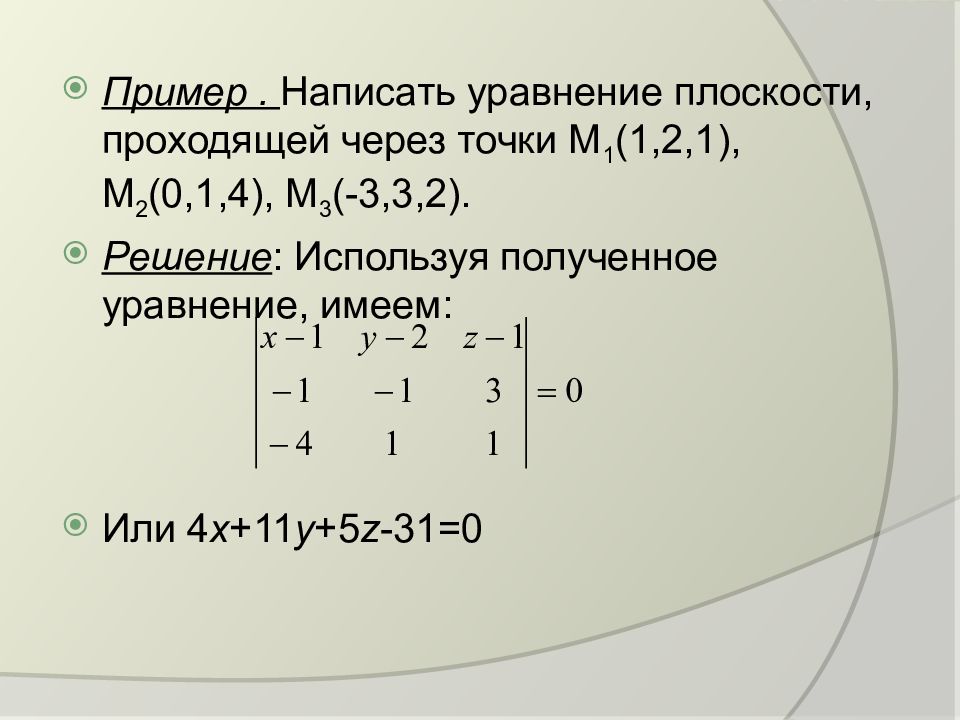
Пример. Написать уравнение плоскости, проходящей через точки M 1 (1,2,1), M 2 (0,1,4), M 3 (-3,3,2). Решение : Используя полученное уравнение, имеем: Или 4 х +11 у +5 z -31=0
Слайд 16: Угол между плоскостями, условие параллельности и перпендикулярности двух плоскостей
Две плоскости: A 1 x + B 1 y + C 1 z + D 1 =0 и A 2 x + B 2 y + C 2 z + D 2 =0. Их нормальные векторы, Углом между двумя плоскостями называется угол между их нормальными векторами Cosω =
Слайд 17
Если плоскости перпендикулярны, то их нормальные векторы тоже перпендикулярны, и поэтому их скалярное произведение равно нулю: А 1 ·А 2 +В 1 ·В 2 +С 1 ·С 2 =0. Если плоскости параллельны, то параллельны их нормальные векторы, а значит, выполняются соотношения:
Слайд 18
Пример : Написать уравнение плоскости, проходящей через точку M (0,1,4) параллельно плоскости 2 х -4 у - z +1=0. Решение : Вектор нормали данной плоскости будет являться нормальным вектором и для искомой плоскости. Используем уравнение плоскости по точке и нормальному вектору: 2( х -0)-4( у -1)-( z -4)=0 или 2 х -4 у - z +8=0.
Слайд 19: Расстояние от точки до плоскости
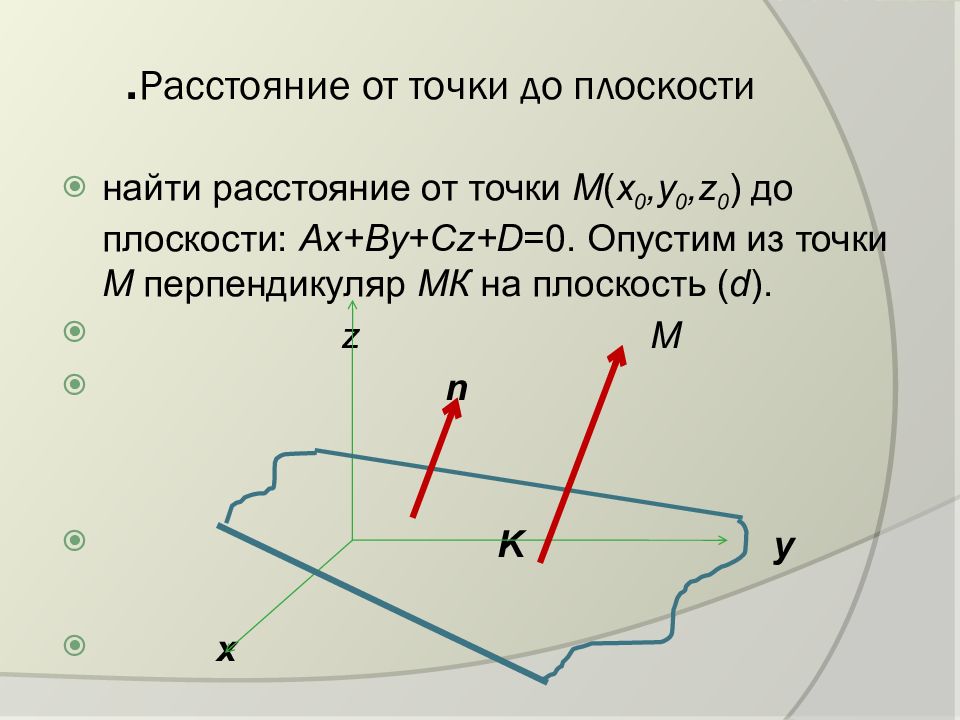
найти расстояние от точки М ( х 0,у 0, z 0 ) до плоскости: Ax + By + Cz + D =0. Опустим из точки М перпендикуляр МК на плоскость ( d ). z M n K y x
Слайд 20
Пусть точка К имеет координаты х 1,у 1, z 1 Или А(х 0 -х 1 )+В(у 0 -у 1 )+С( z 0 - z 1 ) = = Ax 0 + By 0 + Cz 0 -( Ax 1 + By 1 + Cz 1 ). Точка К лежит в плоскости, ее координаты удовлетворяют уравнению плоскости, то есть Ax 1 + By 1 + Cz 1 + D =0.
Слайд 21
Учитывая это, получаем: Ax 0 +By 0 +Cz 0 +D-(Ax 1 +By 1 +Cz 1 +D) = Ax 0 +By 0 +Cz 0 +D. Тогда: Ax 0 + By 0 + Cz 0 + D = ;
Слайд 22
Пример: Найти расстояние от точки М (-1, 2,3) до плоскости 2 х -6 у -3 z +2=0. Решение: Воспользуемся формулой и подставим в уравнение плоскости координаты заданной точки: = =3
Слайд 23: Общие уравнения прямой в пространстве
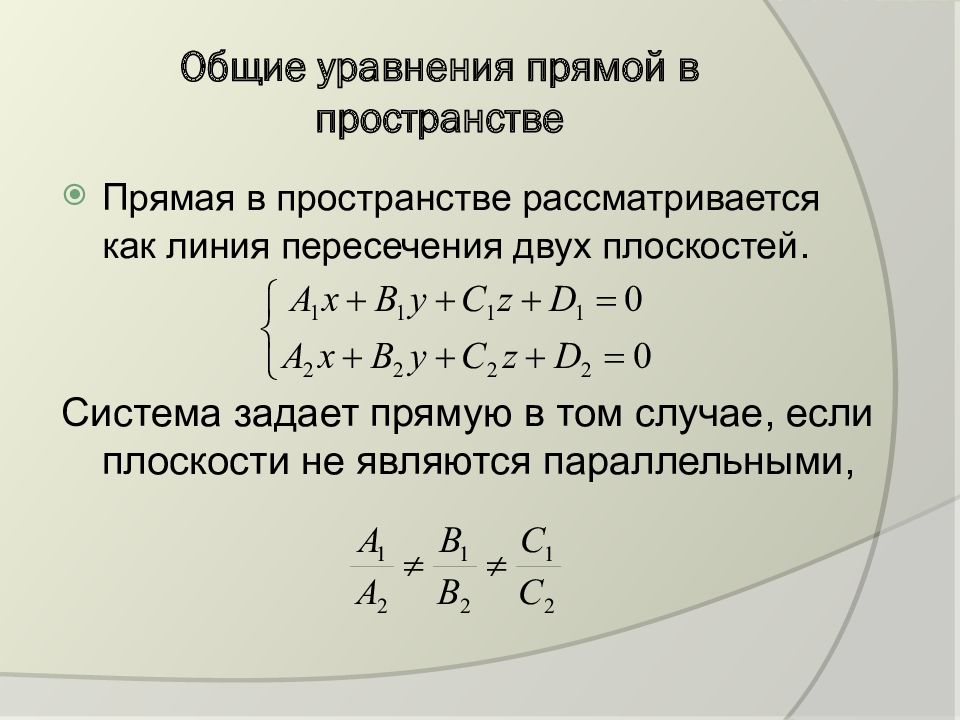
Прямая в пространстве рассматривается как линия пересечения двух плоскостей. Система задает прямую в том случае, если плоскости не являются параллельными,
Слайд 24: Канонические уравнения прямой в пространстве
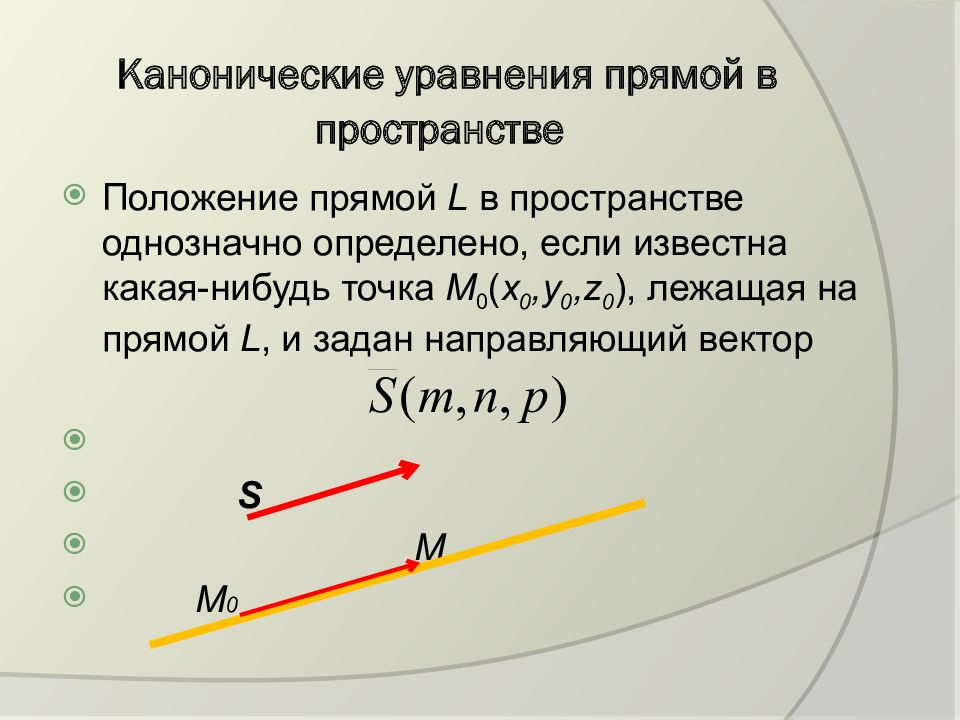
Положение прямой L в пространстве однозначно определено, если известна какая-нибудь точка М 0 ( х 0,у 0, z 0 ), лежащая на прямой L, и задан направляющий вектор S M M 0
Слайд 25
М ( х,у, z ) – произвольная точка на этой прямой. Тогда векторы = ( х-х 0, у-у 0, z - z 0 ) и будут коллинеарны: - канонические уравнения прямой в пространстве или уравнения прямой по точке и направляющему вектору.
Слайд 26
Пример 1 : Написать уравнение прямой L, проходящей через точку М (1,2,3), параллельно прямой Решение: Так как прямые параллельны, то является направляющим вектором и искомой прямой. Следовательно:
Слайд 27
Пример 2 : Написать уравнение прямой L, проходящей через точку М(1,2,3), и имеющей направляющий вектор Решение: Воспользуемся формулой: и у -2=0, то есть 5 х -2 z +1=0 и у =2. Это означает, что прямая лежит в плоскости у =2
Слайд 28: Уравнения прямой в пространстве по двум точкам
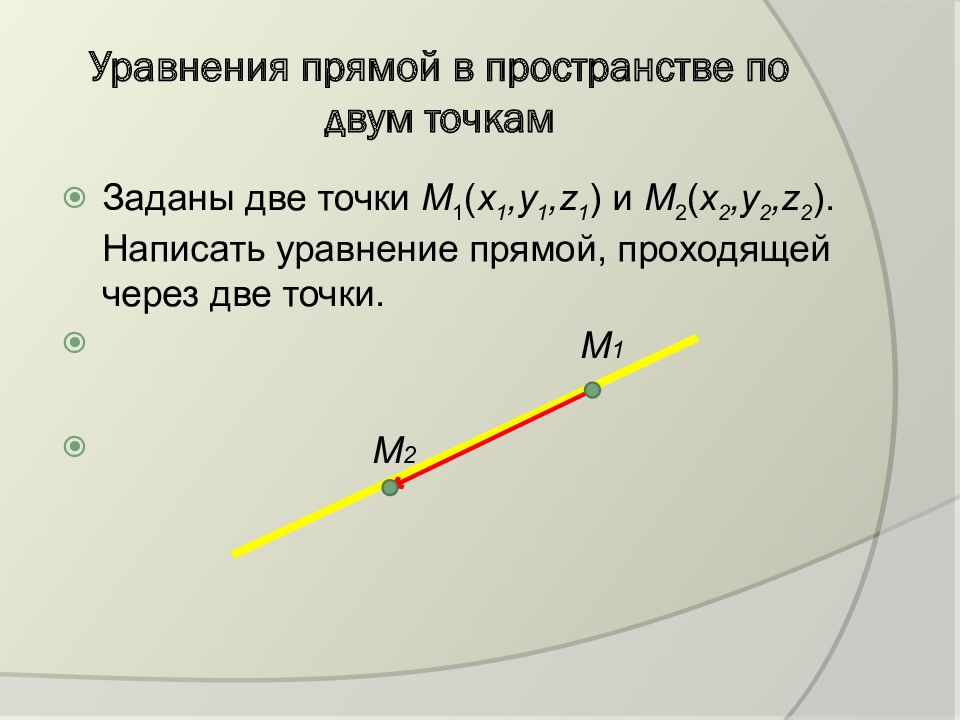
Заданы две точки М 1 ( х 1,у 1, z 1 ) и М 2 ( х 2,у 2, z 2 ). Написать уравнение прямой, проходящей через две точки. М 1 М 2
Слайд 29
Прямая проходит через точку М 1 и имеет в качестве направляющего вектора Уравнение имеет вид: Пример: Написать уравнение прямой, проходящей через точки М 1 (1,4,-3) и М 2 (2,1,1). Решение: Воспользуемся формулой
Слайд 30: Параметрические уравнения прямой в пространстве
Рассмотрим канонические уравнения прямой: Введем параметр t : -∞ < t <+∞.
Слайд 31
Получим: или параметрические уравнения прямой в пространстве. В таком виде их часто используют в механике и физике, параметр t, обычно, время.
Слайд 32: Приведение общих уравнений прямой в пространстве к каноническому виду
Заданы общие уравнения прямой в пространстве (1) Привести их к каноническому виду
Слайд 33
Для решения задачи нужно: 1. найти координаты ( х 0, у 0, z 0 ) какой-либо точки, лежащей на прямой, 2. найти координаты ( m, n, p ) направляющего вектора этой прямой. Чтобы найти координаты точки М 0 придадим одной из координат произвольное численное значение, например полагаем х = х 0. Внеся его в систему (1), получаем систему двух уравнений с неизвестными у и z. Решаем ее. В результате на прямой найдена точка М 0 ( х 0, у 0, z 0 ).
Слайд 34
В качестве направляющего вектора примем вектор, который является результатом векторного произведения нормальных векторов двух плоскостей.
Слайд 35
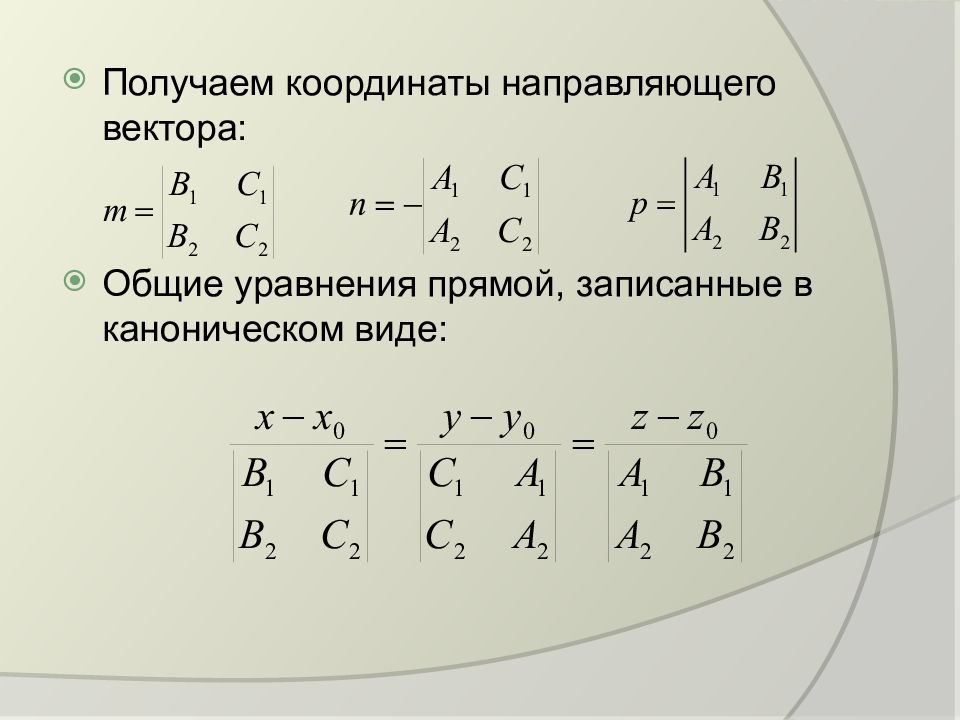
Получаем координаты направляющего вектора: Общие уравнения прямой, записанные в каноническом виде:
Слайд 36
Пример: Записать каноническое уравнение прямой Решение: Положим z 0 =0. Тогда: Отсюда: : у 0 =-6, х 0 =7. Точка М 0, лежащая на прямой, имеет координаты : (7,-6,0).
Слайд 37
Найдем направляющий вектор. Нормальные векторы плоскостей имеют координаты Тогда Канонические уравнения прямой имеют вид:
Слайд 38: Угол между двумя прямыми в пространстве, условие перпендикулярности и параллельности прямых
прямые L 1 и L 2 заданы в каноническом виде с направляющими векторами и
Слайд 39
Углом между двумя прямыми называется угол между их направляющими векторами. cos
Слайд 40
Прямые перпендикулярны, если перпендикулярны их направляющие векторы: То есть, или m 1 m 2 + n 1 n 2 + p 1 p 2 =0. Прямые параллельны, если параллельны их направляющие векторы:
Слайд 41
Пример : Найти угол между прямыми и Решение: Направляющие векторы прямых имеют координаты: (1,3,-2) и (4,1,2). Следовательно,
Слайд 42: Угол между прямой и плоскостью
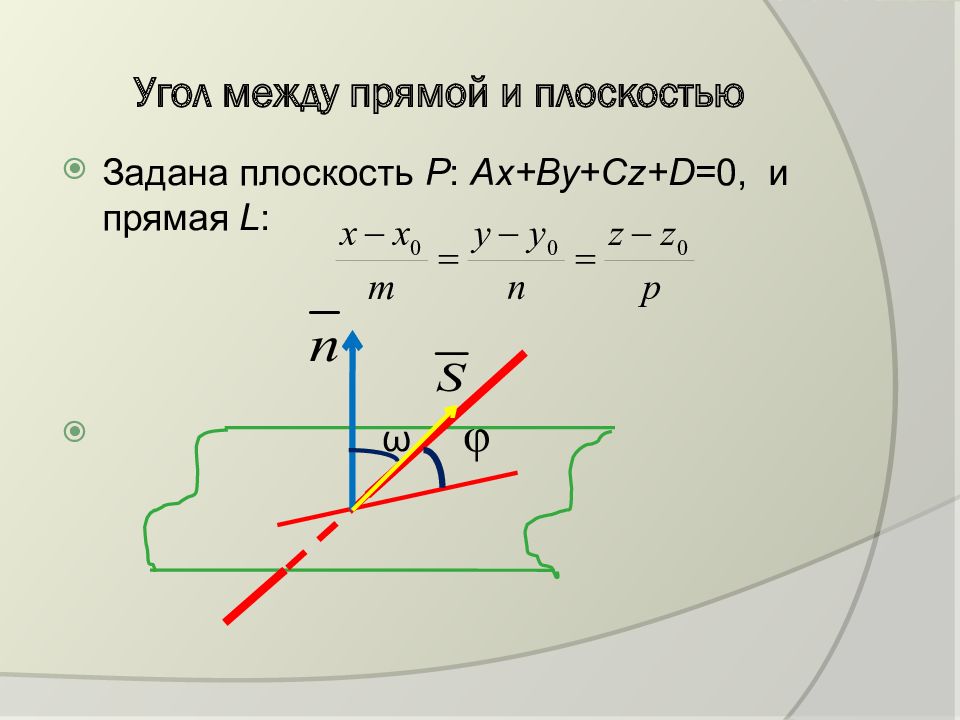
Задана плоскость Р : Ах+Ву+С z + D =0, и прямая L : ω φ
Слайд 43
Углом между прямой и плоскостью называется угол φ между прямой и проекцией ее на плоскость. ω - угол между нормальным вектором плоскости и направляющим вектором прямой. ω = π/2 - φ. Тогда sinφ = cos (π/2-φ )= = cos ω. Но cos ω = cos Тогда sinφ = cos
Слайд 44
sinφ = Пример : Найти угол между прямой: и плоскостью: 2 х + у +2 z -5=0. Решение: Нормальный вектор плоскости имеет координаты: (2,1,2), направляющий вектор прямой имеет координаты: (3,2,-6).
Слайд 45: Условие перпендикулярности и параллельности прямой и плоскости
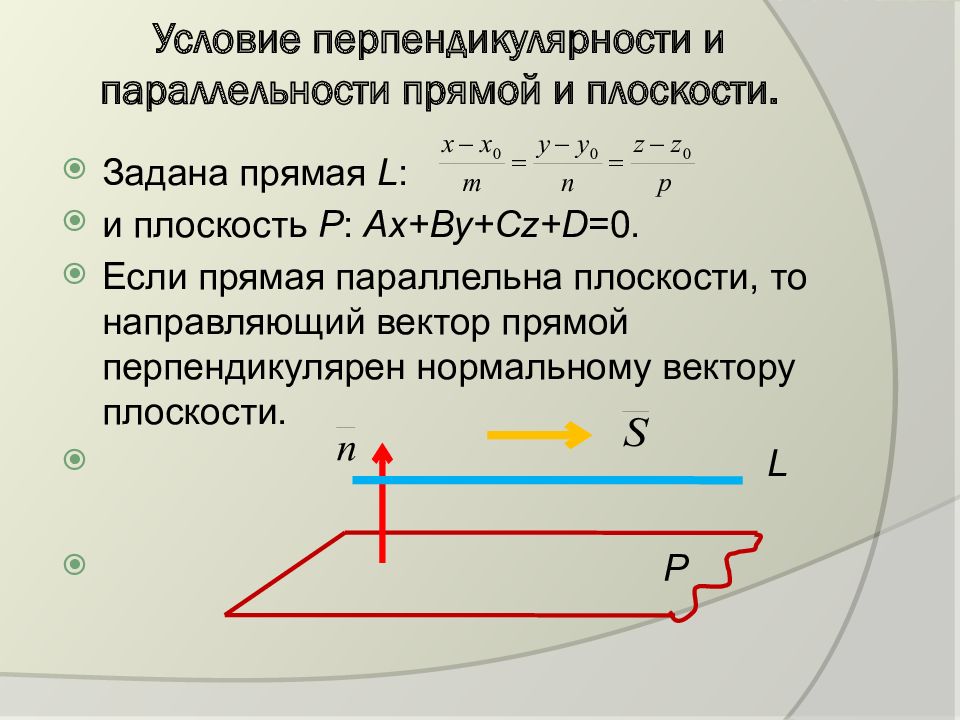
Задана прямая L : и плоскость Р : Ах+Ву+С z + D =0. Если прямая параллельна плоскости, то направляющий вектор прямой перпендикулярен нормальному вектору плоскости. L P
Слайд 46
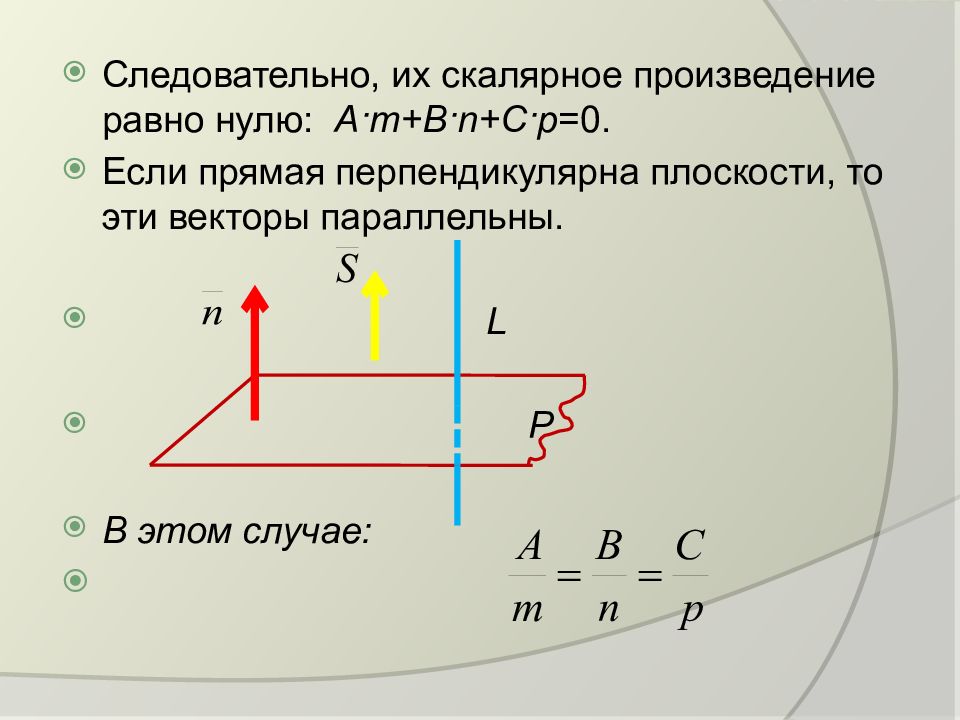
Следовательно, их скалярное произведение равно нулю: A·m + B·n + C·p =0. Если прямая перпендикулярна плоскости, то эти векторы параллельны. L Р В этом случае:
Слайд 47
Пример: Написать уравнение прямой, проходящей через точку М(1,2,-3), перпендикулярно плоскости 4 х +2 у - z +5=0. Решение: Так как плоскость перпендикулярна прямой, то нормальный вектор и направляющий вектор параллельны:
Слайд 48
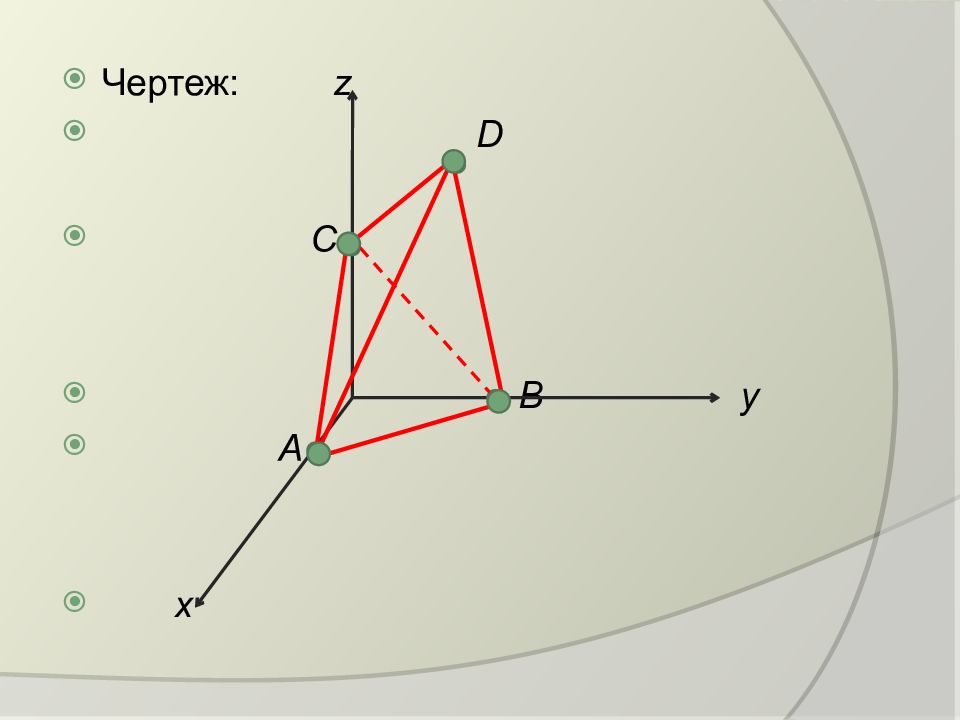
Разберем типовую задачу. Даны вершины пирамиды ABCD : А (1,0,0); B (0,2,0); C (0,0,3), D (2,3,4). Найти: 1. Длину и уравнение ребра АВ, 2. Уравнение и площадь грани АВС, 3. Уравнение и длину высоты, опущенной из вершины D на грань АВС, 4. Угол между ребром AD и гранью АВС, 5. Объем пирамиды.
Слайд 50
1. Введем в рассмотрение вектор. Его координаты: (0-1;2-0;0-0), или (-1;2;0). Длина ребра АВ равна модулю вектора. АВ = Уравнение прямой АВ (уравнение прямой по двум точкам) : Или 2 х + у -2=0
Слайд 51
2. Уравнение грани АВС (уравнение плоскости по трем точкам): Отсюда: ( х -1)∙6- у ∙(-3)+ z ∙2=0, или 6 х +3 у +2 z -6=0. Площадь треугольника АВС найдем с помощью векторного произведения векторов и
Слайд 52
Координаты вектора =(-1;2;0), вектора =(-1,0,3). S Δ ABC = кв.единиц. Векторное произведение:
Слайд 54
Уравнение высоты - уравнение прямой по точке D (2,3,4) и направляющему вектору. В качестве направляющего вектора – нормальный вектор грани АВС: Для нахождения длины высоты используем формулу:
Слайд 55
Получим: 4. Угол между ребром AD и гранью АВС. Уравнение грани АВС : 6 х +3 у +2 z -6=0, нормальный вектор имеет координаты: (6,3,2). Напишем уравнения прямой, проходящей через точки А (1,0,0) и D (2,3,4):
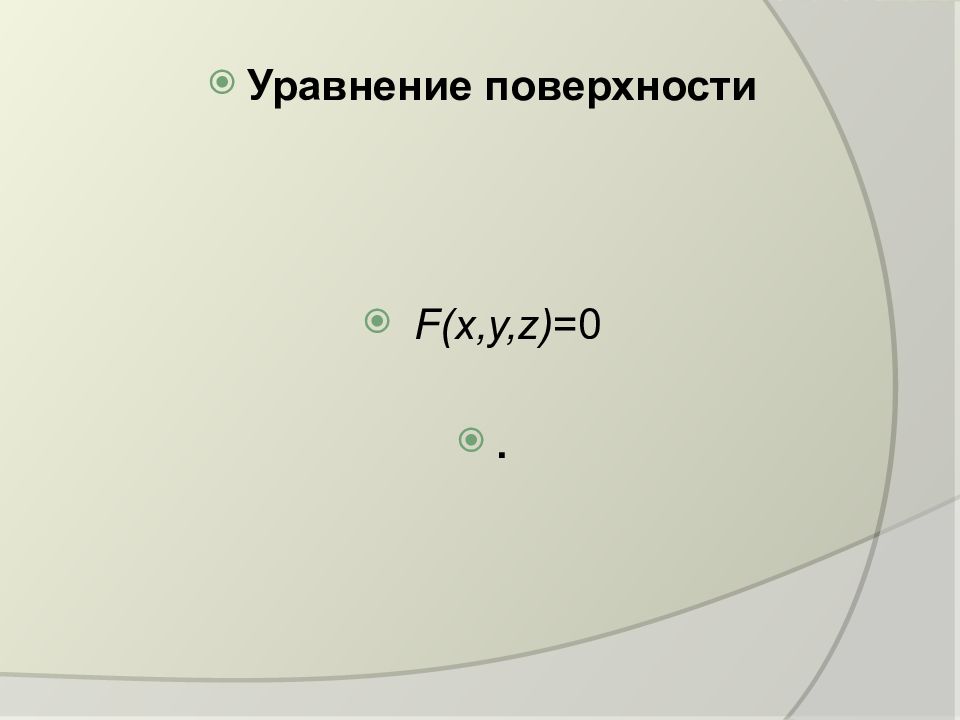
Последний слайд презентации: Уравнение поверхности F ( x, y, z ) =0
5. Объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах, как на сторонах. Используем смешанное произведение векторов. Координаты векторов: =(-1,2,0), =(-1,0,3), =(1,3,4) V параллелепипеда V пирамиды =23/6 куб.ед.