Определение. Кривая называется непрерывной кусочно – гладкой, если функции , и непрерывны на отрезке [ a, b ] и отрезок [ a, b ] можно разбить на конечное число частичных отрезков так, что на каждом из них функции , и имеют непрерывные производные, не равные нулю одновременно. Рассмотрим в пространстве XYZ кривую АВ, в каждой точке которой определена произвольная функция Разобьем кривую на конечное число отрезков и рассмотрим произведение значения функции в каждой точке разбиения на длину соответствующего отрезка. Сложив все полученные таким образом произведения, получим так называемую интегральную сумму функции f ( x, y, z ).
Определение. Если при стремлении к нулю шага разбиения кривой на частичные отрезки существует предел интегральных сумм, то этот предел называется криволинейным интегралом от функции f ( x, y, z ) по длине дуги АВ или криволинейным интегралом первого рода.
Свойства криволинейного интеграла первого рода. 1) Значение криволинейного интеграла по длине дуги не зависит от направления кривой АВ. 2) Постоянный множитель можно выносить за знак криволинейного интеграла. 3) Криволинейный интеграл от суммы функций равен сумме криволинейных интегралов от этих функций. 4) Если кривая АВ разбита на дуга АС и СВ, то
5) Если в точках кривой АВ то 6) Справедливо неравенство : 7) Если f ( x, y, z ) = 1, то S – длина дуги кривой, - наибольшая из всех частичных дуг, на которые разбивается дуга АВ.
8) Теорема о среднем. Если функция f ( x, y, z ) непрерывна на кривой АВ, то на этой кривой существует точка ( x 1, y 1, z 1 ) такая, что Для любой точки М(х, у, z ) кривой длина дуги АМ вычисляется по формуле Длина всей кривой АВ равна: Криволинейный интеграл по длине дуги АВ будет находиться по формуле:
Пусть АВ – непрерывная кривая в пространстве XYZ (или на плоскости ХО Y ), а точка P ( x, y, z ) – произвольная функция, определенная на этой кривой. Разобьем кривую точками на конечное число частичных дуг. И рассмотрим сумму произведений значений функции в каждой точке на длину соответствующей частичной дуги. Определение. Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменной х от функции P ( x, y, z ) по кривой АВ в направлении от А к В.
Вообще говоря, криволинейные интегралы могут считаться также и по переменным у и z. Сумму криволинейных интегралов также называют криволинейным интегралом второго рода.
Свойства криволинейного интеграла второго рода. 1) Криволинейный интеграл при перемене направления кривой меняет знак 2) 3) 4)
5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой. Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным. 6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то Аналогичные соотношения справедливы при интегрировании по переменным у и z.
Теорема. Если кривая АВ – кусочно- гладкая, а функции P ( x, y, z ), Q ( x, y, z ) и R ( x, y, z ) – непрерывны на кривой АВ, то криволинейные интегралы существуют.
Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам: В случае, если АВ – плоская кривая, заданная уравнением y = f ( x ), то
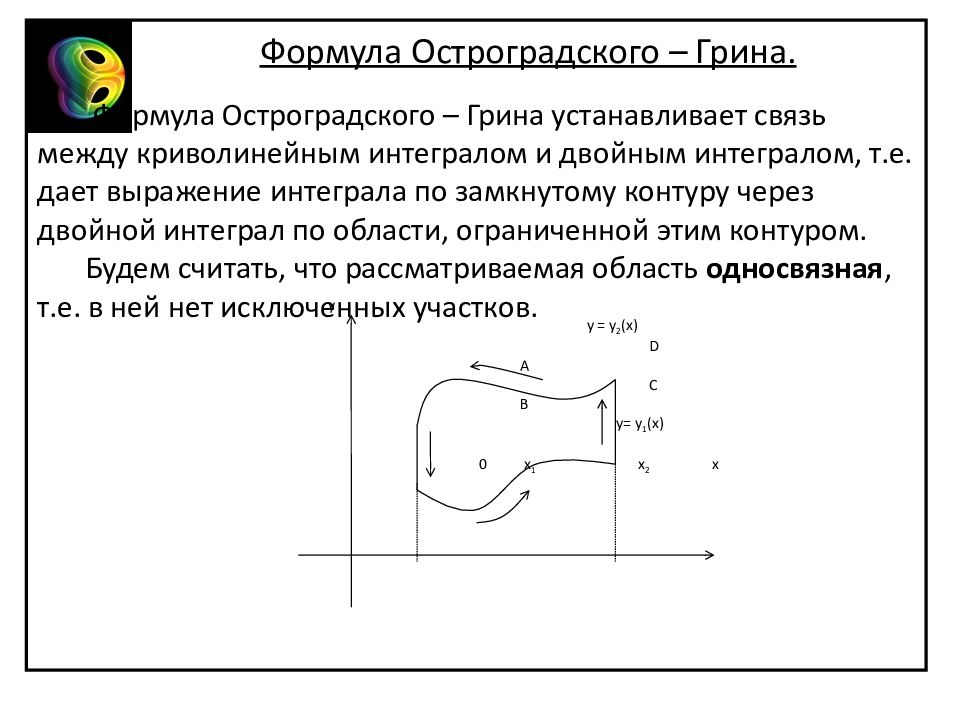
y y = y 2 (x) D A C B y= y 1 (x) 0 x 1 x 2 x Формула Остроградского – Грина. Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром. Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы: Эта формула называется формулой Остроградского – Грина.
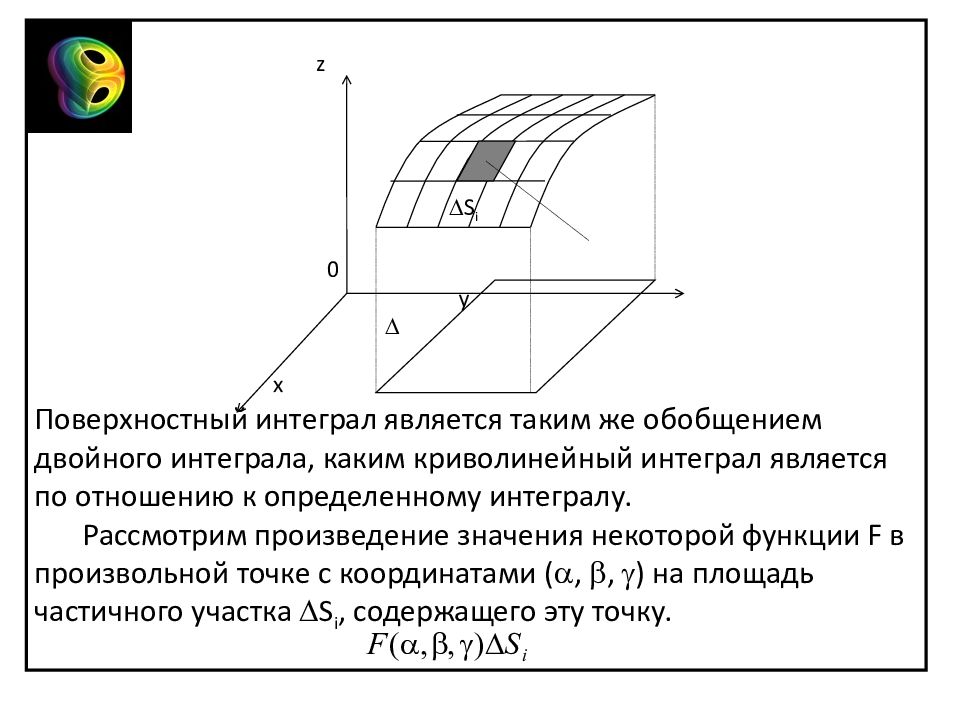
z S i 0 y x Поверхностный интеграл является таким же обобщением двойного интеграла, каким криволинейный интеграл является по отношению к определенному интегралу. Рассмотрим произведение значения некоторой функции F в произвольной точке с координатами ( , , ) на площадь частичного участка S i, содержащего эту точку.
Определение. Если при стремлении к нулю шага разбиения поверхности существует конечный предел интегральных сумм, то этот предел называется поверхностным интегралом первого рода или интегралом по площади поверхности.
Свойства поверхностного интеграла первого рода. 1) S – площадь поверхности. 2) 3) 4) Если поверхность разделена на части S 1 и S 2, то 5) Если , то
6) 7) Теорема о среднем. Если функция F ( x, y, z ) непрерывна в любой точке поверхности S, то существует точка ( , , ) такая, что S – площадь поверхности. Проведя рассуждения, аналогичные тем, которые использовались при нахождении криволинейного интеграла, получим формулу для вычисления поверхностного интеграла первого рода через двойной интеграл по площади проекции поверхности на плоскость XOY.
Рассмотрим в пространстве XYZ ограниченную двухстороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан либо уравнением вида z = f ( x, y ), либо является цилиндрической поверхностью с образующими, параллельными оси OZ. Определение. Если при стремлении к нулю шага разбиения поверхности S интегральные суммы, составленные как суммы произведений значений некоторой функции на площадь частичной поверхности, имеют конечный предел, то этот предел называется поверхностным интегралом второго рода.
- поверхностный интеграл второго рода. Свойства поверхностного интеграла второго рода аналогичны уже рассмотренным нами свойствам поверхностного интеграла первого рода.
Поверхностные интегралы первого и второго рода связаны друг с другом соотношением: В этой формуле cos , cos , cos - направляющие косинусы нормали к поверхности S в выбранную сторону поверхности.
Формула Гаусса – Остроградского. Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными дум другим координатным осям. После этого полученные результаты обобщаются, приводя к формуле Гаусса – Остроградского: На практике формулу Гаусса – Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело. Им еют место формулы :
