1 Первообразная функции и неопределенный интеграл Функция F ( х ) называется первообразной функции f ( х ) на промежутке Х, если в каждой точке х этого промежутка F (х) = f (х). Например, F ( х ) = х 2 /2 является первообразной для функции f ( х ) = х, так как ( х 2 /2) = х. Теорема. Если функция F ( х ) является первообразной функции f ( х ) на промежутке Х, то всякая другая первообразная для функции f ( х ) отличается от F ( х ) на постоянное слагаемое, т.е. может быть представлена в виде: F ( х ) + С, где С – произвольная постоянная. Совокупность всех первообразных для функции f ( х ) на промежутке Х называется неопределенным интегралом от функции f ( х ) и обозначается f ( х ) dx, где - знак интеграла, f (х) – подынтегральная функция, f (х) dx – подынтегральное выражение.
2 Свойства неопределенного интеграла Производная от неопределенного интеграла равна подынтегральной функции, т.е. ( f ( х ) dx ) = f ( х ). Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. d ( f ( х ) dx ) = f ( х ) d х. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. dF ( x ) =F ( x ) + C. Неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же сумме неопределенных интегралов от этих функций, т.е. [ f ( х ) + g ( x )] dx = f ( х ) dx + g ( х ) dx. Постоянный множитель можно выносить за знак неопределенного интеграла, т.е. f ( х ) dx = f ( х ) dx.
3 Таблица основных интегралов.
4 Интегрирование методом разложения. Этот метод основан на разложении подынтегральной функции на сумму функций, от каждой из которых первообразную можно найти с помощью таблицы или других методов. Например ( х 3 + 3 sin x – 8) dx = х 3 dx + 3 sin x dx – 8 dx =< используя формулы из таблицы >= х 4 /4 3 cos x – 8 х + С. Интегрирование методом замены переменных. Интегрирование этим методом заключается в приведении данного интеграла к новому путем замены переменной интегрирования х на новую переменную z. Пусть х = g ( z ), т огда dx = g ( z ) dz. Поэтому f ( х ) dx = f [ g ( z )] g ( z ) dz = Ф ( z ) +С = Ф [ g -1 ( х )] + С.
5 Интегрирование по частям. Пусть u ( x ) и v ( x ) – две функции от х, имеющие непрерывные производные, тогда справедлива следующая формула: udv = uv - vdu. Эта формула называется формулой интегрирования по частям и позволяет свести данный интеграл к более простому Пример
6 Интегрирование рациональной дроби Задача интегрирования сводится к интегрированию простейших дробей следующих четырех типов: Здесь, β=2, 3, …; λ=2, 3, …; B, M, N, b, p и q – некоторые вещественные числа, причем трехчлен x 2 +px+q не имеет вещественных корней, т.е. q-p 2 /4>0. При этом справедлива следующая теорема:
7 Теорема. Всякая рациональная дробь интегрируема в элементарных функциях. Действительно, если произвести подстановку t=x-b, то дроби первого и второго типа будут интегрируемы в элементарных функциях т. е. Квадратные трехчлены третьей и четвертой дробей можно представить в виде (x 2 +px+q)=(x+p/2) 2 +(q-p 2 /4) и, учитывая, что (q-p 2 /4)>0, ввести вещественную постоянную и сделать подстановку t=x+p/2, тогда задача интегрирования может быть решена с использованием известных формул интегрирования.
8 Пример 1 :
9 Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
10 Пример 1 :
11 Интегрирование тригонометрических функций При нахождении интегралов от тригонометрических функций используется ряд методов: Использование тригонометрических формул Понижение степени подынтегральной функции Метод замены переменной
12 Пример 2:
13 Понижение степени подынтегральной функции
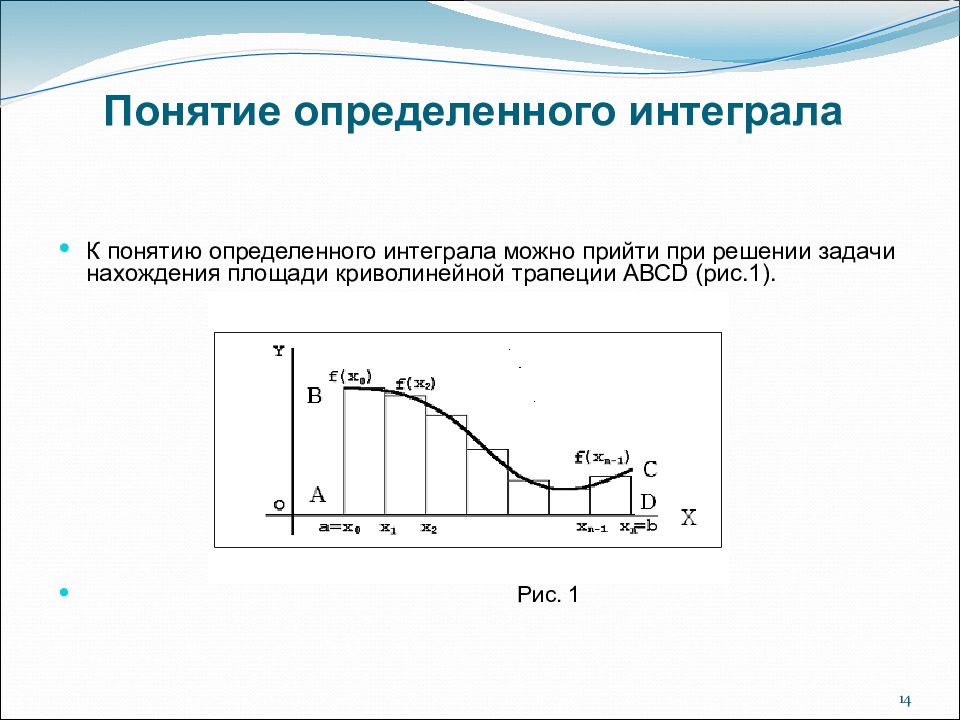
14 Понятие определенного интеграла К понятию определенного интеграла можно прийти при решении задачи нахождения площади криволинейной трапеции АВС D (рис.1). Рис. 1
15 Пусть функция y = f ( x ) определена и непрерывна на интервале [ a, b ]. Требуется вычислить площадь, ограниченную отрезком графика функции на интервале изменений аргумента от x=a до x=b. Для решения задачи разобьем рассматриваемый интервал значений аргумента на малые промежутки, ограниченные точками a=x o <x 1 <x 2 <...x n =b. Можно считать, что на каждом промежутке от x k-1 до x k значение функции f(x) меняется мало. Поэтому приближенно значение функции на указанном промежутке будем считать постоянным и равным, например, f(x k ). В таком случае площадь, ограниченная функцией f(x) на промежутке изменения аргумента ∆x k =x k -x k-1, приближенно равна f(x k )∆x k, а полная площадь S на интервале от a до b приблизительно равна S ≈ f ( x 1 )∆ x 1 + f ( x 2 )∆ x 2 +... + f ( x n )∆ x n.
16 При уменьшении всех промежутков ∆x k мы будем получать все более и более точное значение площади S, а точное значение площади мы получим, перейдя в сумме к пределу при стремлении всех ∆x k к нулю (при этом количество слагаемых будет возрастать): В математике предел данной суммы называется определенным интегралом от функции f(x) в пределах от a до b и обозначается символом т.е.
17 Определенным интегралом называется предел n- ой интегральной суммы при Геометрический смысл определенного интеграла : это площадь криволинейной трапеции, ограниченной слева прямой х=а, справа прямой x=b, сверху кривой y=f(x), снизу осью Ох.
18 Свойства определенного интеграла
19 если то Теорема о среднем. Пусть функция f(x) непрерывна на [a,b], тогда найдется такая точка, что
20 Теорема. Пусть функция y = f ( x ) непрерывна на интервале [ a, b ] и F ( x ) –любая первообразная для f ( x ) на [ a, b ]. Тогда определенный интеграл от функции f ( x ) на [ a, b ] равен приращению первообразной F ( x ) на этом интервале, т. е. (1) Формула (1) – формула Ньютона-Лейбница. Она утверждает, что определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования. Для вычисления определенного интеграла нужно найти первообразную подынтегральной функции (неопределенный интеграл) и из значения первообразной при верхнем приделе вычесть значение первообразной при нижнем пределе интегрирования
21 Пример 1 Вычислить интеграл Применяя формулу Ньютона-Лейбница, получаем
22 Методы вычисления определенного интеграла. Если - непрерывно дифференцируемая на отрезке функция,, и когда t изменяется на, то, положив, получим формулу замены переменной в определенном интеграле:
23 Методы вычисления определенного интеграла Пусть - непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям:
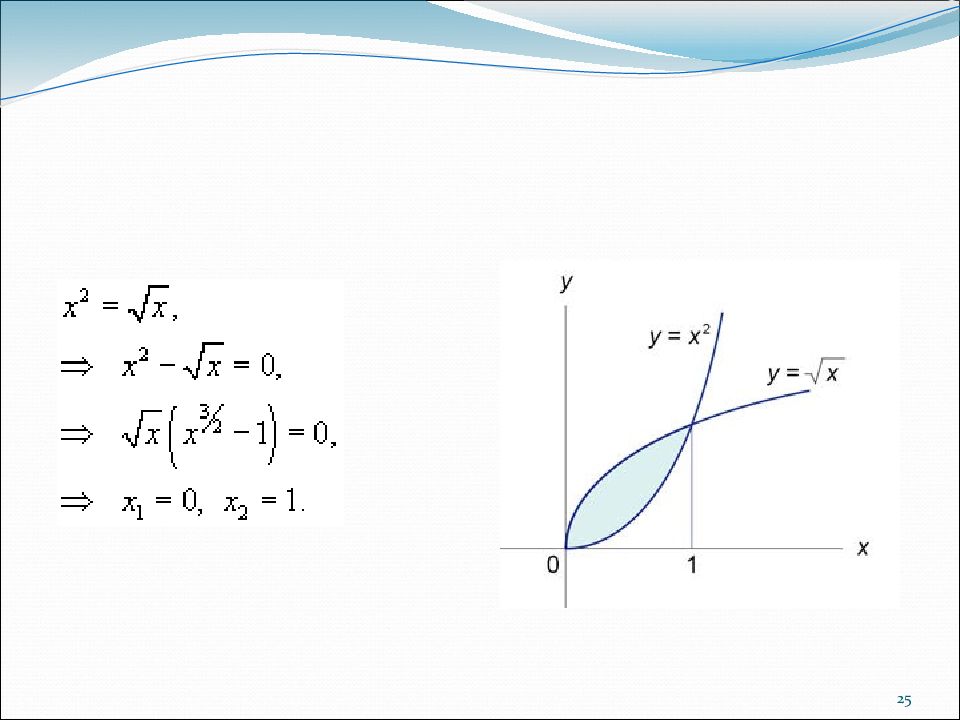
24 Пример 2 Найти площадь фигуры, ограниченной кривыми Решение. Сначала определим точки пересечения двух кривых (рисунок 1 ).
25
26 Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно площадь фигуры:
27 Несобственный интеграл Пусть функция f ( x ) определена в промежутке [ a,+∞)и интегрируема в любой конечной ее части. Несобственным интегралом функции f ( x ) называется и обозначается символом. Интеграл называется сходящимся, если указанный предел конечен, и расходящимся, если предел бесконечен или не существует. Пусть функция f ( x ), заданная в конечном промежутке [ a, b ], не ограничена в любой окрестности точки с этого промежутка. Несобственный интеграл
