1
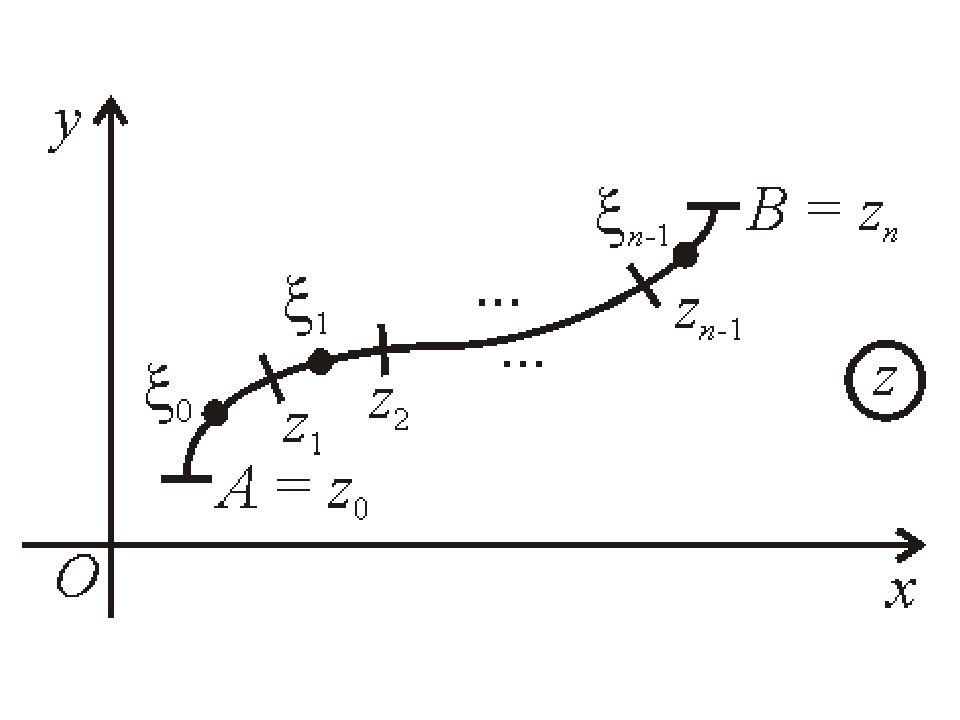
§ 1. Интегрирование функции комплексного переменного. Пусть на комплексной плоскости задана кривая AB – ориентированная, незамкнутая, кусочно-гладкая, без самопересечений. Задание кривой z(t) эквивалентно следующему:
и – действительные числа. x(t), y(t) – действительные числа. Разобьем AB произвольным образом: Найдем разности двух составляющих комплексного числа. На каждом из участков выберем произвольные точки
Они отвечает соответствующим комплексным числам. Пусть на комплексной плоскости, в том числе и на дуге AB определена комплексная функция f(z). Найдем ее значения в точках: и составим сумму вида: - это интегральная сумма.
Определение. (интеграла) Если существует предел интегральной суммы не зависящий от способа разбиения дуги AB и выбора точек, то этот предел называют интегралом по дуге AB и обозначают:
Теорема. (о существовании интеграла от функции комплексного переменного) Пусть функция f(x) непрерывна на некоторой кривой L, которая является ориентируемой, кусочно-гладкой, незамкнутой, тогда интеграл по дуге L от этой функции существует. Доказательство. Рассмотрим интегральную сумму
Так как любую функцию комплексного переменного можно представить в виде: Комплексное число можно представить в виде Перемножим эти выражения (1)
Значит в использованном выражении (1), интегральная сумма может быть записана в виде: (2) Перейдем к пределу в выражении (2), получим: 9
Так как f(z) непрерывна на L, то непрерывны в любой точке u и v (т.к задание f(z) равносильно заданию u и v ) В правой части (3) – интегральные суммы для криволинейных интегралов 2 рода Из непрерывности u и v следует, что существуют криволинейные интегралы 2 рода как предел своих интегральных сумм. 10
Так как каждый из пределов входящий, входящий в правую часть (3) существует и равен соответствующему криволинейному интегралу, то существует и предел левой части (3) и можем записать (4) (4) может использоваться и для вычисления интегралов от ФКП. 11
Свойства интегралов от ФКП. Если L + и L - д ве дуги, различающиеся только ориентацией, то: 2) 3) 4) М – действительное число l – длина дуги L 12
13 § 2. Понятие первообразной. Формула Ньютона-Лейбница. Интегрирование по частям и заменой переменной. Пусть функция f(z) задана в некоторой односвязной области D на комплексной плоскости. Если существует функция F(z) в области D, такая что F (z) = f(z), то F(z) называется первообразной для функции f(z).
14 Теорема. (о первообразной) Если функция f(z) дифференцируема в замкнутой, односвязной области D, то для нее существует первообразная F(z ), определенная на D, которая задается формулой: Замечание 1 : В отличии от функции действительного переменного функцию комплексного переменного необходимо дифференцировать в замкнутой односвязной области для существования первообразной.
15 Замечание 2 : Е сли f(z) непрерывна в односвязной области D, и интеграл по любому замкнутому контуру, лежащему в этой области =0, то в этом случае первообразная так же существует. Замечание 3 : Две первообразные ФКП отличаются на константу.
16 Теорема. (Ньютона- Лейбница) Если f(z) дифференцируема в односвязной области D и z 1, z 0 произвольные точки D, а F(z) какая либо первообразная для f(z), то Теорема. (интегрирование по частям) Если f(z) и ( z ) дифференцируемы в односвязной области D, z 1, z 0 – точки, принадлежащие D, то
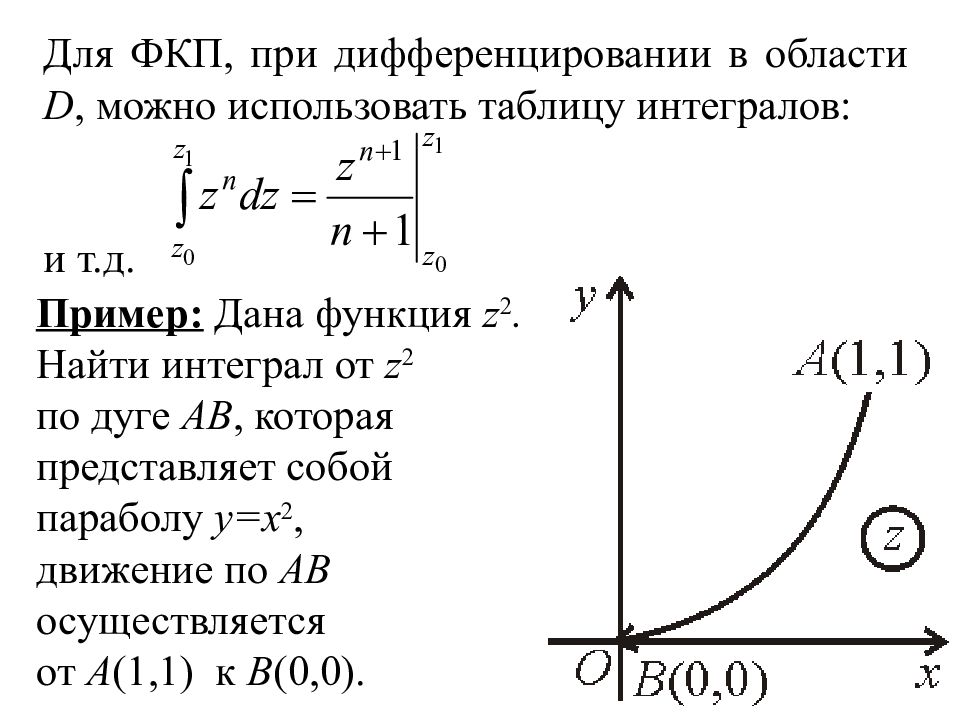
17 Пример: Дана функция z 2. Найти интеграл от z 2 по дуге AB, которая представляет собой параболу y=x 2, движение по AB осуществляется от A (1,1) к B (0,0). Для ФКП, при дифференцировании в области D, можно использовать таблицу интегралов: и т.д.
z 2 = ( x + iy ) 2 = x 2 – y 2 + i 2 xy u v тогда:
19 2 - й способ решения с помощью формулы Ньютона-Лейбница:
20 § 3. Интегральная теорема Коши. Если функция f(z) аналитична в односвязной замкнутой области D, то интеграл от этой функции по любому замкнутому контуру, лежащему в этой области = 0, то есть: L - произвольный контур. Доказательство. Так как f(z) аналитична в области D, значит она дифференцируема в односвязной области D ; из дифференцируемости следует существование интеграла в области D по любой кривой.
21 Из аналитичности следует выполнение условий Коши-Римана Пусть L - произвольный, ориентированный замкнутый контур, в области D, тогда (1) формула Грина Из аналитичности f(z) следует дифференцируемость в области. Применим к криволинейному интегралу 2-го рода, стоящему в правой части (1) формулу Грина:
22 0 0 D * - область, лежащая внутри L Из условий Коши-Римана имеем, что подынтегральное выражение = 0. Значит интеграл от аналитической односвязной функции = 0 по любому замкнутому контуру. Если область D не является односвязной теорему в этой формулировке применить нельзя
Теорема. Если функция f ( z ) аналитична в неодносвязанной замкнутой области D с конечным числом вырезов, то f ( z ) dz по границе области D, обходимый в положительном направлении = 0. Без доказательства. Следствие теоремы Коши для неодносвязанной области. Если f ( z ) аналитична в неодносвязанной области D с границей L, то справедлива следующая формула: 23
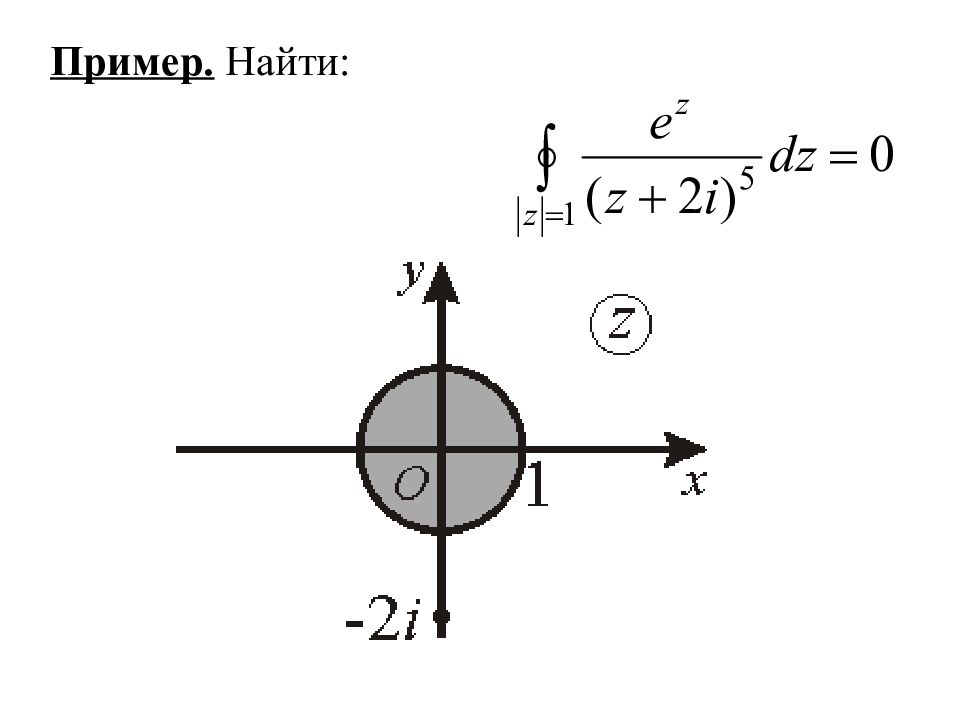
L i – граница вырезов, обход которой производится в том же направлении, что и обход границы L. § 4. Некоторые основные формулы интегрального исчисления. Теорема. (интегральная формула Коши). Если функция f ( z ) аналитична в замкнутой односвязанной области D с положительно ориентированной, кусочно-гладкой границей L, то значение функции в любой точке z k D находится по формуле: 24
Примечание. Значения функции в области определяются своими значениями на границе. Без доказательства. Интеграл Коши Пусть функция f ( z ) аналитична в некоторой области D лежащей на комплексной плоскости. Пусть в области D имеется ориентированный замкнутый контур L. Точка L. Интегралом типа Коши в области D называется интеграл вида: Точки z лежат либо внутри, либо вне контура L. 25
Свойства интеграла Коши Если z лежит вне контура L, z D, то для z D, z L. 2. Если z лежит внутри контура L, z D, то Значение функции аналитической в области определяется значением на границе. 26
Если кривая L незамкнута, то говорят об интеграле типа Коши где - незамкнутая ориентируемая кривая, лежащая в области D. Интеграл типа Коши обозначают: 27
Замечание. Если функция f ( z ) дифференцируема в области D, кривая L замкнутая граница области D, то интеграл Коши является бесконечно дифференцируемой в области функцией, причем: 28
Пример. Найти:
