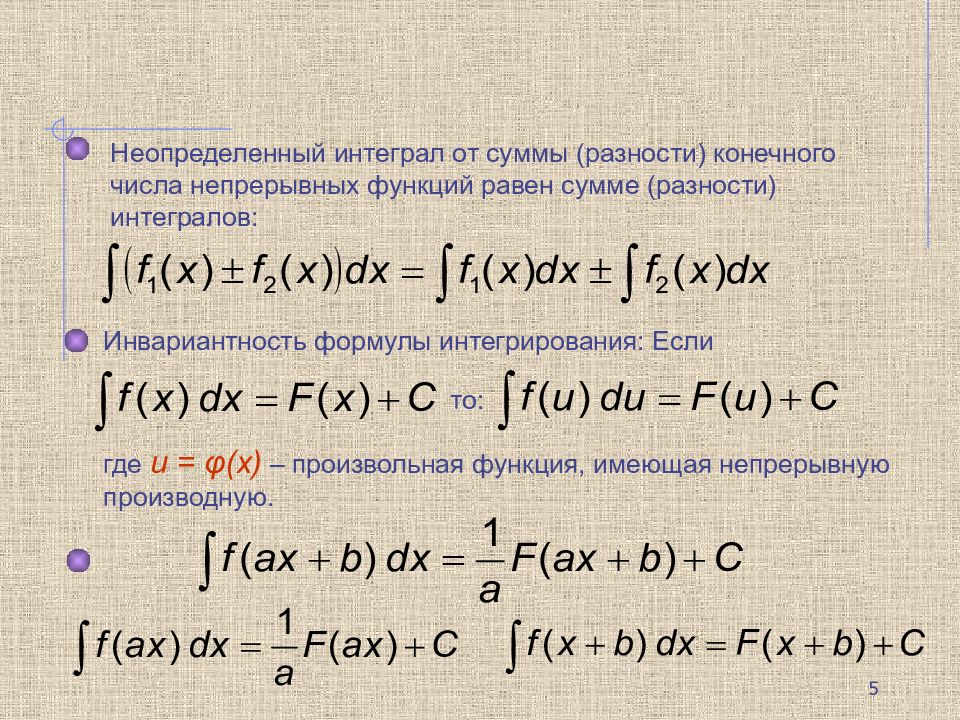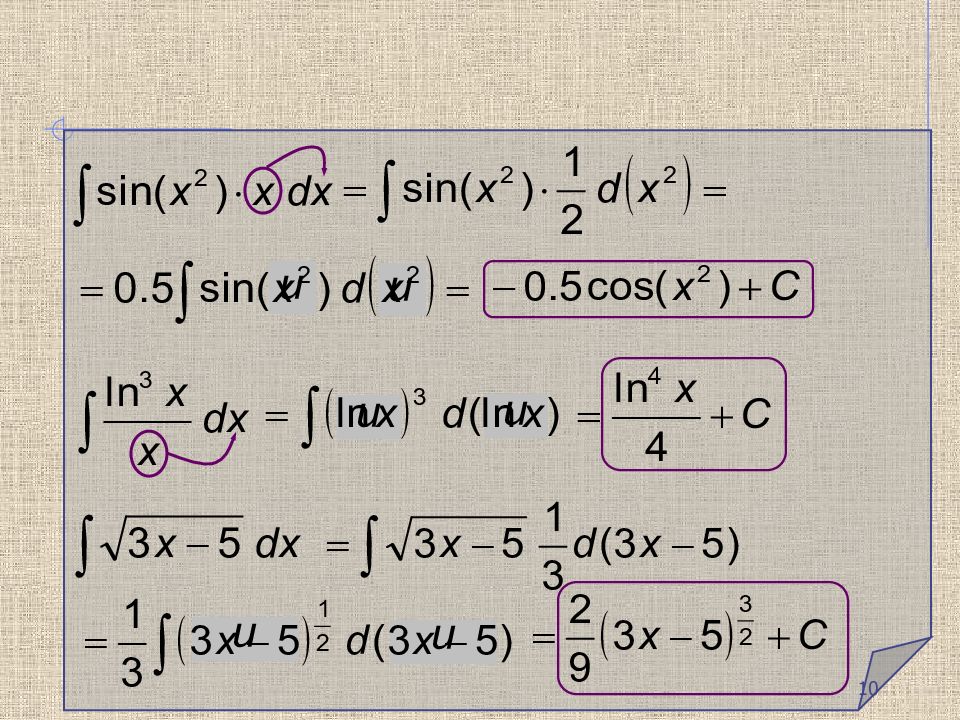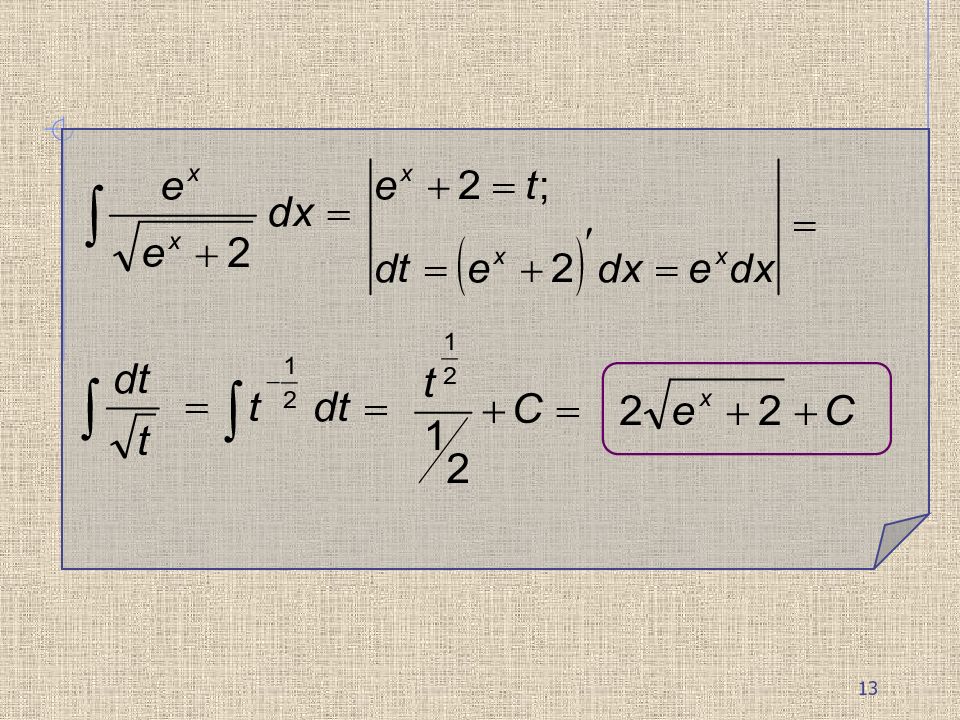Понятие неопределенного интеграла Свойства неопределенного интеграла Таблица интегралов Непосредственное интегрирование Введение части функции под знак дифференциала Метод замены переменной Метод интегрирования по частям 1
В дифференциальном исчислении решается задача: по данной функции f(x) найти ее производную. Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F’(x) = f(x) : Функция F(x) называется первообразной функции f(x) на интервале ( a; b), если Теорема Если функция F(x) является первообразной функции f(x) на ( a; b), то множество всех первообразных для f(x) задается формулой: F(x) + С, где С – постоянное число. Доказательство: F(x) + С – первообразная функции f(x). 2
Знак неопределенного интеграла Переменная интегрирования Подынтегральное выражение Подынтегральная функция Операция нахождения неопределенного интеграла от функции называется называется интегрированием этой функции. Множество всех первообразных функций F(x) + С для f(x) называется неопределенным интегралом от функции f(x) и обозначается: Геометрически неопределенный интеграл представляет собой семейство параллельных кривых y = F(x) + С ( интегральных кривых ) y 0 х y = F(x) + С 1 y = F(x) + С 2 y = F(x) + С 3 3
Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная от неопределенного интеграла равна подынтегральной функции: Благодаря этому свойству правильность интегрирования проверяется дифференцированием. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной. Постоянный множитель можно выносить за знак неопределенного интеграла. 4
Неопределенный интеграл от суммы (разности) конечного числа непрерывных функций равен сумме (разности) интегралов: Инвариантность формулы интегрирования: Если то: где u = φ(x) – произвольная функция, имеющая непрерывную производную. 5
6
7
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к табличным интегралам, называется непосредственным интегрированием. 8
При сведении данного интеграла к табличному часто применяются следующие преобразования дифференциала ( операция « подведения под знак дифференциала ») 9
10
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. Пусть требуется вычислить интеграл Сделаем подстановку:, где φ – функция, имеющая непрерывную производную. Тогда: Получим формулу интегрирования подстановкой : Иногда целесообразно подбирать подстановку в виде Тогда подынтегральную функцию нужно представить в виде: t dt 11
12
13
Интегрируя это равенство, получим: Интегрирование по частям состоит в том, что подынтегральное выражение представляется в виде произведения двух сомножителей: u и dv, затем, после нахождения du и v используется формула (1). Иногда эта формула применяется несколько раз. Пусть u = u(x) и v = v(x) - функции, имеющие непрерывную производную. Тогда: Формула интегрирования по частям (1) 14
Интегралы вида: где: P(x) – многочлен. Удобно положить u = P(x), dv – остальные сомножители. Типы интегралов, которые удобно вычислять по частям: Интегралы вида: Удобно положить dv = P(x)dx, u – остальные сомножители. Интегралы вида: - интегралы, приводящиеся к исходному. За u можно принимать любой сомножитель. 15
u dv u v v du 16
u dv I 1 17
u dv 18
