Лекция № 9 Первое начало термодинамики. 1. Внутренняя энергия. 2. Макроскопическая работа. 3. Теплота. 4. Первое начало термодинамики. 5. Теплоемкость идеального газа. Теорема Майера. 6. Адиабатический процесс. 7. Обратимые и необратимые процессы 8. Условия преобразования теплоты в механическую работу
Внутренняя энергия. Важнейшей характеристикой термодина-мической системы является ее внутренняя энергия. Это энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) плюс энергия взаимодействия этих частиц. Из этого определения следует, что к внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.
Внутренняя энергия – функция состояния, то есть в каждом из состояний, характеризуемых параметрами P,V,T, система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). При переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от процесса (от пути перехода). Итак, в каждом из состояний система обладает определенным значением внутренней энергии, а ее изменение можно вычислить:
Малое изменение внутренней энергии математически записывается как - полный дифференциал. Если рассматривать круговой процесс, в ходе которого система проходит ряд состояний и возвращается в первоначальное состояние, изменение внутренней энергии равно нулю: Это следует из того, что U есть функция состояния.При возврате в начальное состояние U также возвращается к исходному значению. Внутренняя энергия определяется с точностью до аддитивной постоянной: энергию одного из состояний можно принять за нулевую (U = 0).
Для идеального газа под внутренней энергией подразумевают лишь энергию теплового хаотического движения молекул, так как взаимодействие между молекулами пренебрежимо мало. Внутренняя энергия газа, содержащего N молекул: где - средняя кинетическая энергия молекулы, ; где - число молей. Для одноатомного газа и Для газа с более сложными молекулами i — число степеней свободы молекул (зависит от их структуры)
Макроскопическая работа А (работа, связанная с перемещением тел) . Рассмотрим газ, находящийся под поршнем в цилинд-рическом сосуде. Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то он производит над ним элементарную работу где - площадь поршня, - изменение объема. Таким образом,
Полную работу, совершаемую газом при изменении его объема от до находим интегрированием формулы для элементарной работы: Результат интегрирования определяется характером зависимости давления от объема газа. Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах.
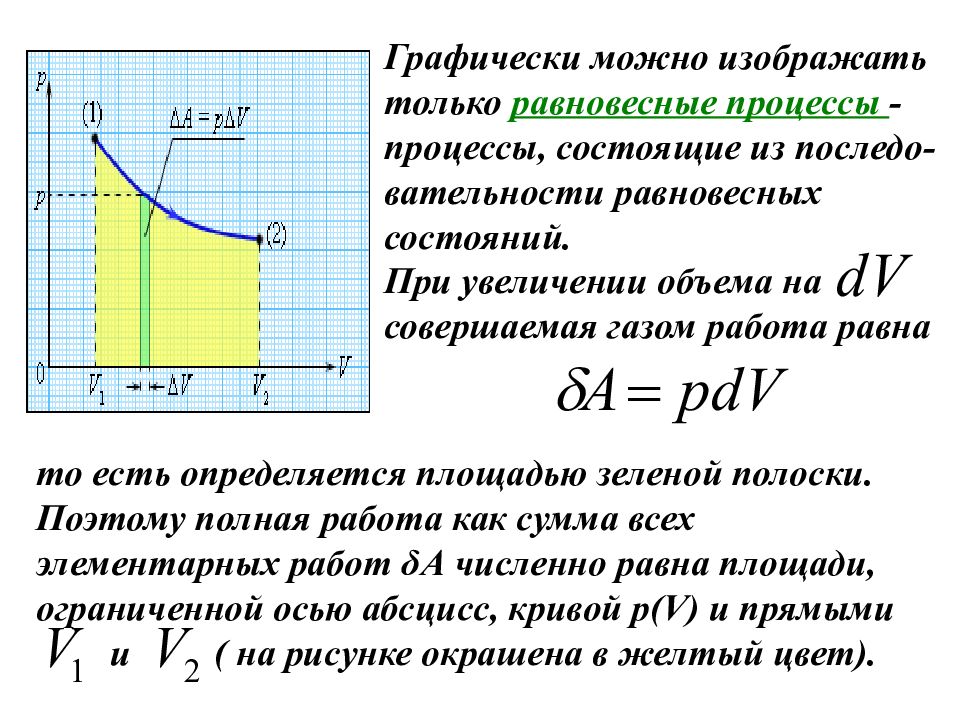
Графически можно изображать только равновесные процессы - процессы, состоящие из последо-вательности равновесных состояний. При увеличении объема на совершаемая газом работа равна то есть определяется площадью зеленой полоски. Поэтому полная работа как сумма всех элементарных работ δА численно равна площади, ограниченной осью абсцисс, кривой p(V) и прямыми и ( на рисунке окрашена в желтый цвет).
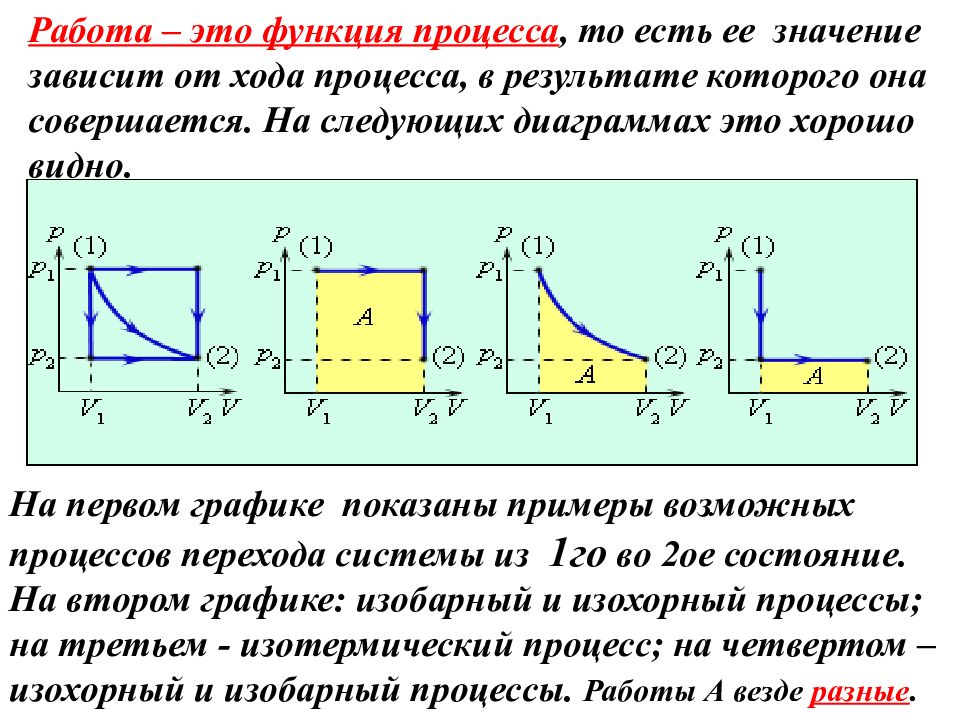
Работа – это функция процесса, то есть ее значение зависит от хода процесса, в результате которого она совершается. На следующих диаграммах это хорошо видно. На первом графике показаны примеры возможных процессов перехода системы из 1го во 2ое состояние. На втором графике: изобарный и изохорный процессы; на третьем - изотермический процесс; на четвертом – изохорный и изобарный процессы. Работы А везде разные.
В качестве примера рассчитаем работу газа в изотермическом процессе. По определению Из уравнения М-К: В изотермическом процессе Т=const,поэтому
Мы рассмотрели работу газа, совершаемую под действием его давления р газ.Для квазистатических процессов давление р газ уравновешено внешним давлением р внеш, поэтому Определение макроскопической работы: работа внешних сил, связанная с перемещением оболочки (движением поршня), называется макроскопической работой.
Теплота. Количество теплоты Q. Изменение внутренней энергии возможно за счет : 1) работы внешних сил и 2) перехода внутренней энергии от более нагретого тела к менее нагретому. Процесс обмена внутренними энергиями соприкасающихся тел, не сопровождающийся совершением макроскопической работы, называется теплопередачей или теплообменом. Энергия, переданная в результате теплообмена, называется количеством теплоты или просто теплотой.
Процесс передачи энергии происходит в результате столкновений молекул более нагретого тела с молекулами менее нагретого – то есть в результате микроскопической работы. Количество теплоты Q является функцией процесса, то есть оно зависит от характера процесса, в котором оно передается. Единица измерения теплоты в системе СИ - [Q] = Дж. Менее распространенной в настоящее время единицей измерения теплоты является калория. Связь калории с джоулем называется механическим эквивалентом теплоты: 1 кал = 4,18 Дж
Первое начало термодинамики. Первое начало термодинамики представляет собой закон сохранения энергии применительно к тепловым процессам. Изменение внутренней энергии термодинамической системы возможно в результате сообщения ей теплоты и совершения над системой внешней работы: Это одна из формулировок первого начала.
Используя,, получим: Тогда окончательно: Количество тепла, сообщенное термодинамической системе, идет на приращение ее внутренней энергии и на совершение этой системой работы над внешними телами. Будем использовать именно эту формулировку первого начала термодинамики. Кроме того, в дальнейшем обозначим.
Для квазистатических процессов, когда параметры испытывают бесконечно малые изменения, I-ое начало принимает вид: В этом выражении является полным дифференциалом (приращением функции состояния системы), а и - элементарной работой и элементарной теплотой (зависят от вида процесса). Вернемся к предыдущей формуле Если, это означает, что система получает тепло Если - система отдает тепло. Если А>0 — работу совершает газ. Если А<0 — работа совершается над газом.
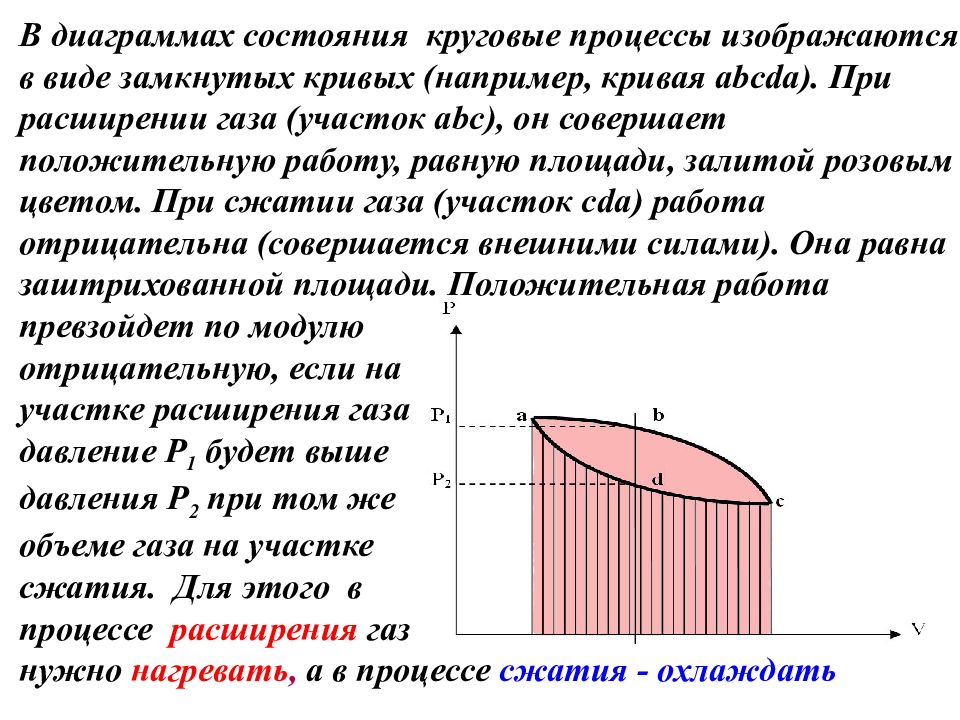
Следствия из первого начала. 1) В круговом процессе ( на рис. abcd) Это означает, что I-ое начало не накладывает никаких ограничений на преобразование теплоты в механическую работу, и в результате кругового процесса может совершаться работа. 2) Если и, то. Это означает, что невозможен процесс, единственным результатом которого является производство работы без каких-либо изменений в других телах. То есть невозможен вечный двигатель первого рода.
Теплоемкость идеального газа. Уравнение Майера. Численно теплоёмкость тела равна количеству теплоты, необходимой для нагревания этого тела на один Кельвин. Теплоёмкость – это способность системы накапливать тепло. Размерность теплоемкости: [C] = Дж/К. Теплоёмкость тел зависит от их массы, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Удельная теплоёмкость С уд – есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 кельвин : ; Для газов удобно пользоваться молярной теплоем-костью С μ Это количество теплоты, необходимое для нагревания 1 моля газа на 1 кельвин , [ C μ ] = Дж / (моль · К), [C уд ] = Дж/ ( кг · К). число молей
Нагревание газа можно производить в условиях постоянного объема или давления. Соответственно различают теплоемкости при постоянном объеме и постоянном давлении. Запишем выражение первого начала термодинамики для одного моля газа с учетом выражений для теплоемкости и работы в то же время значит Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (dV μ =0) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
В дальнейшем С μV будем для краткости обозначать С V Если газ нагревается при постоянном давлении, то теплоемкость можно записать в виде: Дифференцируя уравнение Менделеева-Клайперона PV μ = RT по Т (при р = const), получаем:
Тогда окончательно: Уравнение называется уравнением Майера. Оно показывает, что всегда больше на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнитель-ное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Из сказанного следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобарическом процессе.
Адиабатический процесс Адиабатическим называется процесс, идущий без теплообмена с окружающей средой: Из первого начала получаем т.е. работа совершается за счет изменения внутренней энергии системы. Выведем уравнение адиабатического процесса Для одного моля газа перепишем написанное выше уравнение в виде: (1)
Продифференцировав уравнение состояния для идеального газа, получим : (2) ( 1) Почленно разделим уравнение (2) на (1), получим Здесь учтено, что С р - С V =R. Кроме того, обозначим получим или
Интегрируя это уравнение в пределах от до и соответственно от до, придем к выражению: затем потенцируем: В итоге Так как состояния 1 и 2 выбраны произвольно, то можно записать Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Обратимые и необратимые процессы Все термодинамические процессы делят на две группы: обратимые и необратимые. Обратимым процессом называется такое изменение состояния системы (или одного тела), которое будучи проведено в обратном направлении, возвращает ее в исходное состояние так, чтобы система прошла через те же промежуточные состояния, что и в прямом процессе, при этом состояние тел вне системы остается неизменным. В частности, механические движения в отсутствие сил трения являются обратимыми.
В термодинамике свойством обратимости обладают только равновесные процессы. Каждое промежуточное состояние является состоянием термодинамического равновесия, нечувствительного к тому, идет ли процесс в прямом или обратном направлении. Например, обратимым можно считать процесс адиабатического расширения или сжатия газа. При адиабатическом расширении газа условие теплоизолированности системы исключает непосредственный теплообмен между системой и средой. Поэтому, производя адиабатическое расширение газа, а затем сжатие, можно вернуть газ в исходное состояние так, что в окружающей среде никаких изменений не произойдет.
Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния. Все процессы, происходящие в природе естествен-ным образом, являются необратимыми: выравнивание разности температур (теплопроводность); выравнивание давлений выравнивание концентраций (диффузия). Все это процессы перехода в состояние термодинамического равновесия.
Не только в природе, но и в технике в реальных условиях всегда имеется некоторая необратимость процесса, обусловленная, например, несовершенством теплоизоляции, трением при движении поршня и т.д. Только в обратимых процессах теплота используется по назначению, не расходуется напрасно.. В необратимых процессах происходит частичная диссипация (рассеяние) энергии.
Условия преобразования теплоты в механическую работу Вся практика показывает, что механическую энергию можно полностью превратить в теплоту. А возможно ли это сделать наоборот: теплоту полностью преобразовать в механическое движение? Такой вопрос возник при создании тепловых машин. Обратимся к первому началу т/д Если, то. Так для изотермичес-кого процесса работа по расширению газа
Казалось бы нет ограничений на превращение теплоты в механическую работу. Однако рассмотренный случай относится к однократному акту передачи теплоты. Тепловые же машины работают циклически, то есть процессы передачи тепла и преобразования его в работу периодически повторяются. Рассмотрим свойства круговых процессов, которые реализуются в тепловых машинах. Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическая система возвращается в исходное состояние.
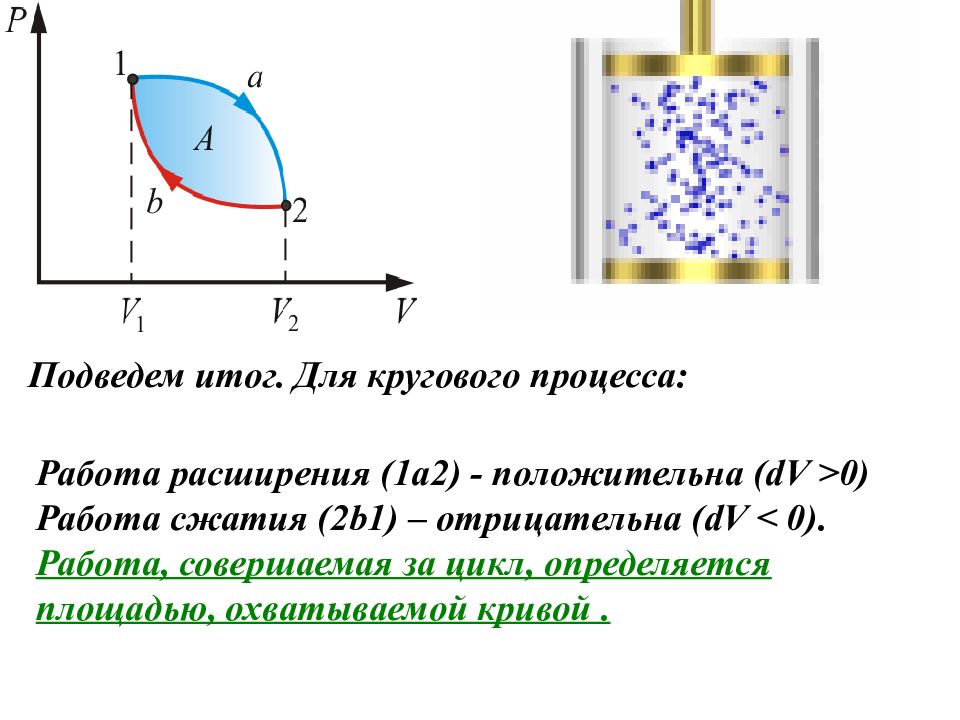
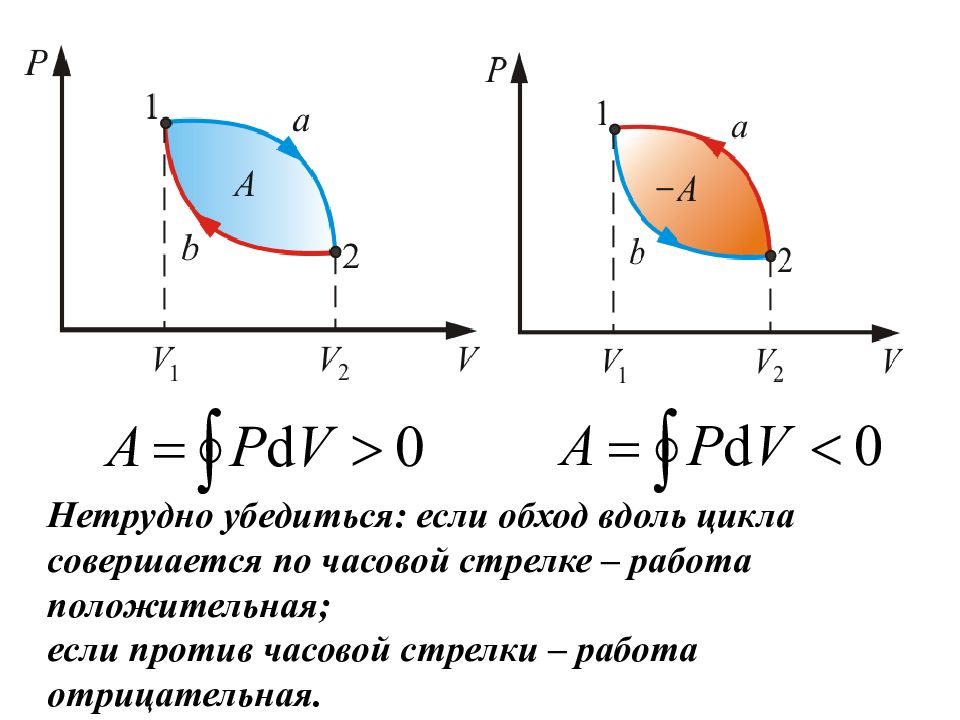
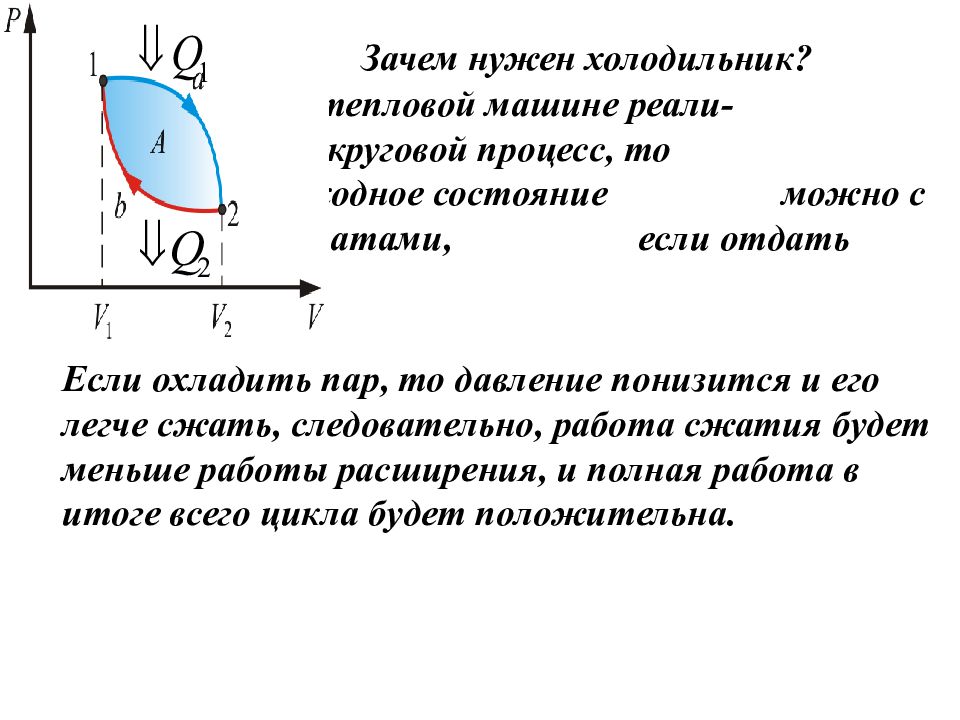
Подведем итог. Для кругового процесса: Работа расширения (1a2) - положительна (dV >0) Работа сжатия (2b1) – отрицательна (dV < 0). Работа, совершаемая за цикл, определяется площадью, охватываемой кривой.
Нетрудно убедиться: если обход вдоль цикла совершается по часовой стрелке – работа положительная; если против часовой стрелки – работа отрицательная.
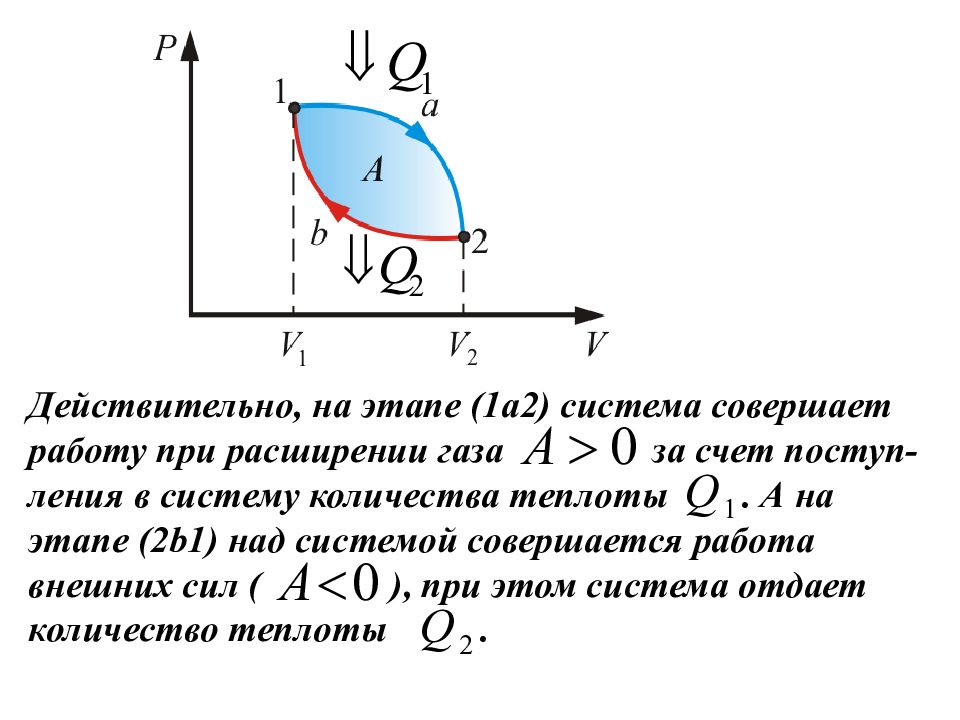
В результате кругового процесса система возвраща-ется в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю: Тогда первое начало термодинамики для кругового процесса дает Однако в ходе кругового процесса система на одном участке процесса теплоту получает, на другом - отдает, поэтому Q1 – количество теплоты, полученное системой; Q2 – количество теплоты, отданное системой.
Действительно, на этапе (1а2) система совершает работу при расширении газа за счет поступ-ления в систему количества теплоты. А на этапе (2b1) над системой совершается работа внешних сил ( ), при этом система отдает количество теплоты.
Опыт и практика показывает, что всю теплоту, взятую из теплового резервуара, ни в каком циклическом процессе не удается полностью превратить в механическую работу.
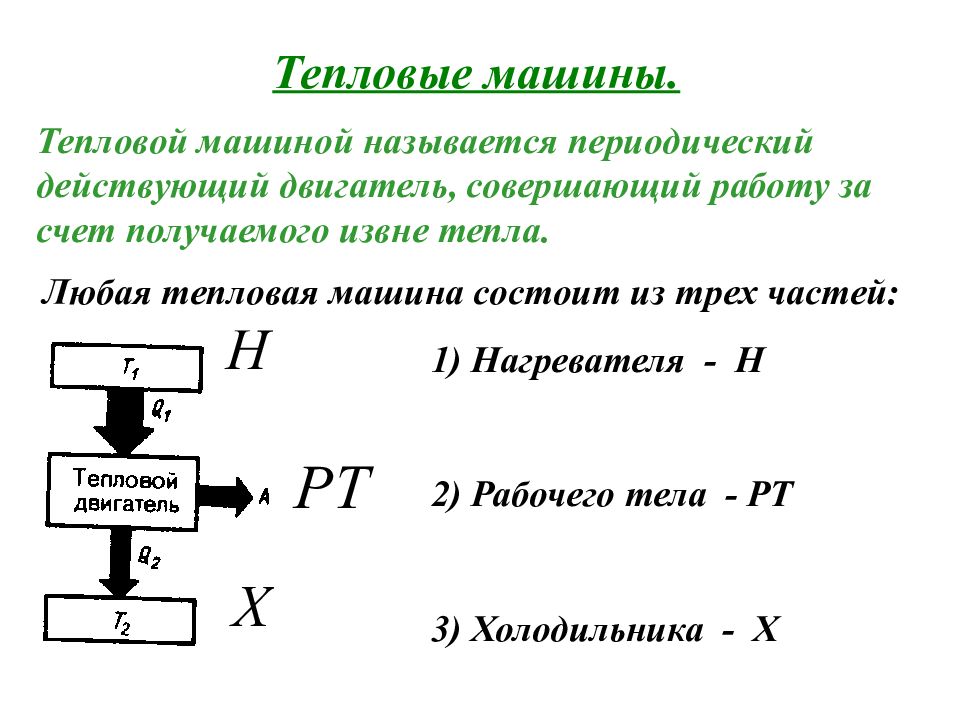
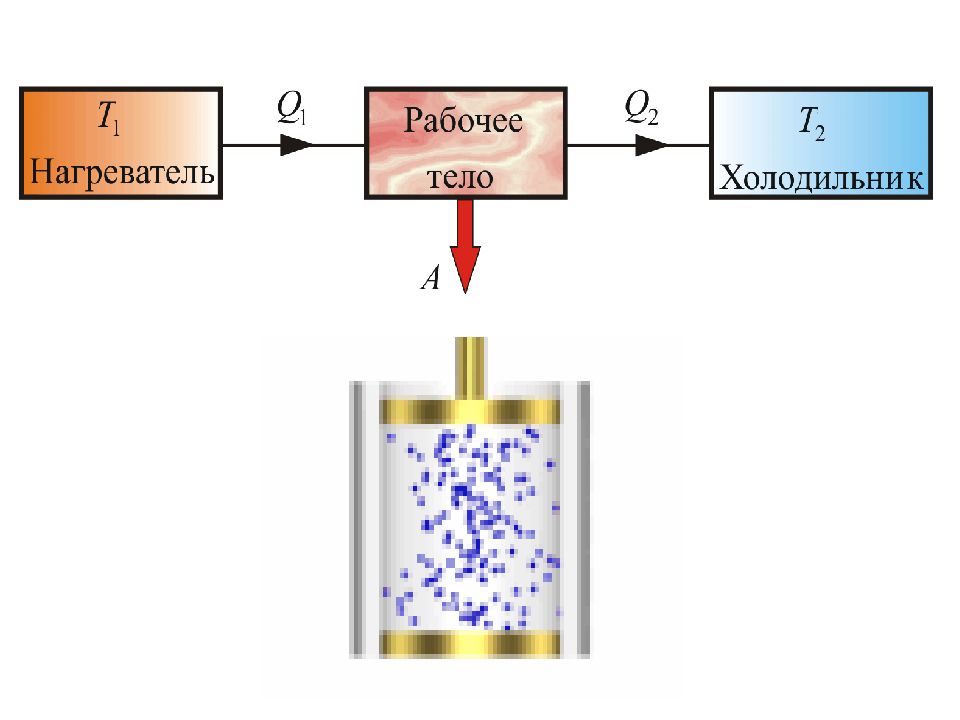
Тепловые машины. Тепловой машиной называется периодический действующий двигатель, совершающий работу за счет получаемого извне тепла. Любая тепловая машина состоит из трех частей: 1) Нагревателя - Н 2) Рабочего тела - РТ 3) Холодильника - Х
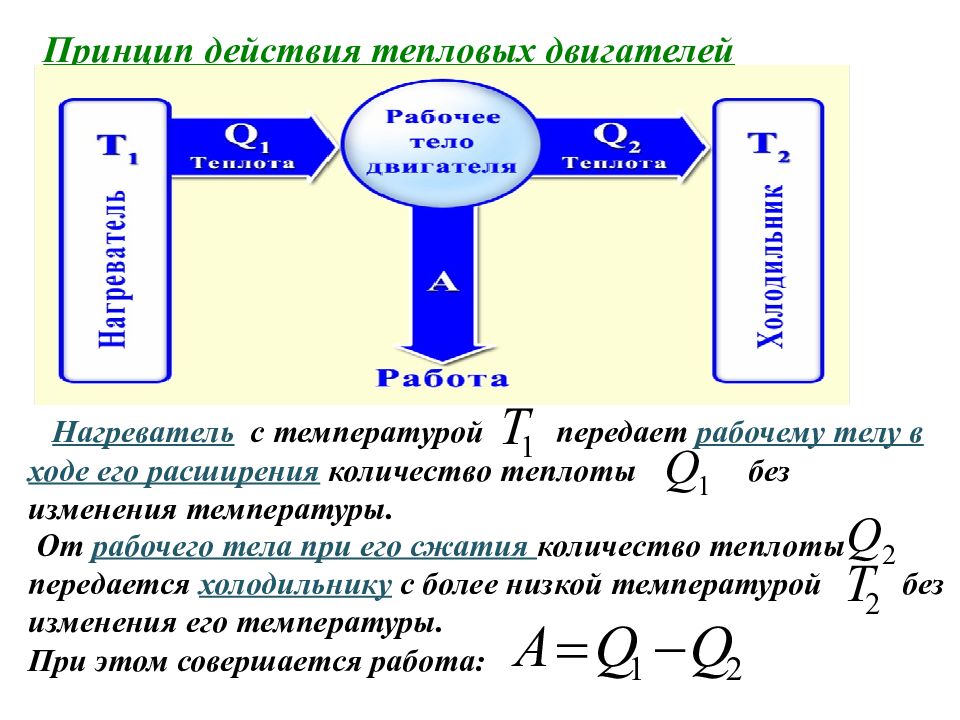
Принцип действия тепловых двигателей Нагреватель с температурой передает рабочему телу в ходе его расширения количество теплоты без изменения температуры. От рабочего тела при его сжатия количество теплоты передается холодильнику с более низкой температурой без изменения его температуры. При этом совершается работа:
Важнейшей характеристикой тепловой машины является коэффициент полезного действия КПД : где - коэффициент полезного действия- КПД- теплового двигателя; - полезная работа, совершенная двигате- лем, Дж; - количество теплоты, полученное двигате- лем, от нагревателя Дж.
Зачем нужен холодильник? Так как в тепловой машине реали - зуется круговой процесс, то вернуться в исходное состояние можно с меньшими затратами, если отдать часть тепла. Если охладить пар, то давление понизится и его легче сжать, следовательно, работа сжатия будет меньше работы расширения, и полная работа в итоге всего цикла будет положительна.
КПД тепловых двигателей Паровая машина КПД = 15% Турбореактивный двигатель КПД = 20 -30% Двигатель внутреннего сгорания КПД =25-30% Газовая турбина КПД = 25 – 29% Паровая турбина КПД = 25 - 40%
