Урок "открытия" нового знания
Приведение дробей к общему знаменателю урок математики в 6 классе, пункт учебника № 10
Обучающие - контроль и оценка знаний, умений и навыков, связанных с основным свойством дроби, сокращением дробей и приведением дробей к новому знаменателю; изучение действия приведения дробей к наименьшему общему знаменателю. Развивающие – развивать внимание, зрительную память, логическое мышление, математическую речь, смекалку, умение самооценивать и анализировать свои ошибки; Воспитательные – воспитывать активность стремления к учебе, уважение друг к другу; формировать бережное отношение учащихся к своему здоровью. Цели:
Запись дробей и действия с ними были так сложны, что учение о дробях считалось самым трудным разделом арифметики. Чтобы его освоить, приходилось заучивать огромное число правил действий с дробями. Современная система записи дробей с числителем и знаменателем была создана в Индии, только там не писали дробной черты. А записывать дробь в точности так, как сейчас, стали арабы. Общеупотребительной эта запись дробей стала лишь в XVI веке.
Объясните основное свойство дроби. Что значит сократить дробь? Всякую ли дробь можно сокращать? Какую дробь называют несократимой? Приведите примеры. Как нужно сокращать дробь, чтобы получить несократимую дробь? в с п о м н и :
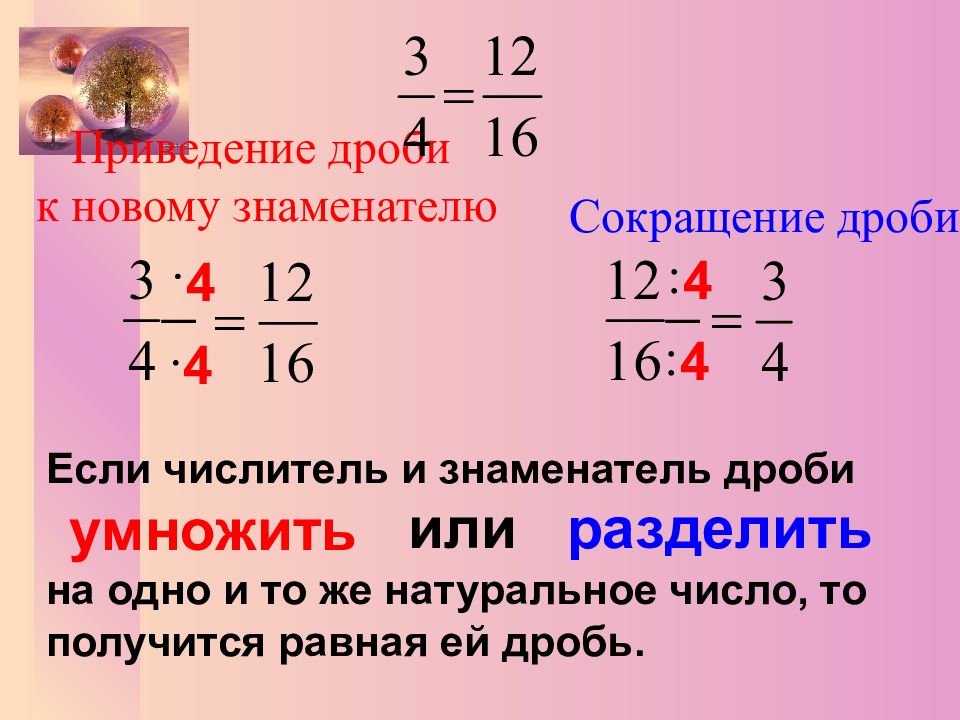
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получиться равная ей дробь. основное свойство дроби
Чтобы привести дроби к общему знаменателю, надо: 1) подобрать наименьший общий знаменатель; 2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель ; 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь. или разделить 4 4 4 4 Сокращение дроби Приведение дроби к новому знаменателю
Умножение числителя и знаменателя на одно и тоже число, отличное от единицы, называют приведением дроби к новому знаменателю. А число, на которое умножается и числитель и знаменатель называют дополнительным множителем. 3 3 3 Приведение дроби к новому знаменателю
,,,,,,,,
К какому наименьшему общему знаменателю можно привести дроби и ? Как привести дроби и к общему знаменателю? К какому наименьшему общему знаменателю можно привести дроби и ? выполним вместе
Приведите к наименьшему общему знаменателю дроби: а), б), в), г), д), е), ж), з). № 1
В 6 «А» классе девочки составляют всех учащихся класса, а мальчики - всех учащихся класса. Кого в классе больше мальчиков или девочек? Решение: Девочек - уч. Мальчиков - уч. ? Так как, то >. Значит девочек в классе больше.
В 2 В 1 В 3 Дроби 1/7 и 1/3 Дроби 1/3 и 1/5 Дроби 1/6 и 1/8 Дроби 1/5 и 1/7 В 4 1. замените равными им дробями со знаменателем 48 30 63 70 2. Приведите дроби к наименьшему общему знаменателю 11/15 и 3/5 2/3 и 3/5 5/18 и 4/12 6/13 и 7/52 3. Приведите дроби к наименьшему общему знаменателю 1/4 и 1/7 4/21 и 2/7 3/7 и 5/9 4/18 и 5/63 4. Приведите дроби к наименьшему общему знаменателю 3/15 и 4/25 6/33 и 5/9 2/3 и 7/12 4/11 и 7/9 5. Сравните дроби 22/37 и 43/74 17/28 и 35/56 15/41 и 29/82 28/39 и 85/117 Самостоятельная работа
В 1 В 2 В 3 В 4 8/48 и 6/48 10 / 30 и 6 / 48 9 / 63 и 21 / 63 14 / 70 и 10 / 70 11/15 и 9/15 10 / 15 и 9 / 15 10 / 36 8 и 12 / 36 24 / 52 и 7 / 52 7/28 и 4/28 4 / 21 и 6/ 21 27 / 63 и 35 / 63 28 / 126 и 10 / 126 15/75 и 12/75 1 8/ 99 и 55 / 99 8/ 12 и 7 / 12 36 / 99 и 77/99 22/37 > 43 / 74 17 / 2 8 < 35 / 56 15 / 41 > 23 /8 2 2 8/ 39 < 85 / 117 1 2 3 4 5 Проверь себя :
Верно ли утверждение? При сложении дробей с одинаковыми знаменателями знаменатель остаётся тем же, а числители складываются. Чтобы вычесть дроби с разными знаменателями, надо привести их к наименьшему общему знаменателю и выполнить вычитание дробей с одинаковыми знаменателями. Чтобы сложить смешанные числа, надо сложить их целые части и отнять сумму дробных частей. Если при сложении дробей получается неправильная дробь, то надо результат записать в виде смешанного числа. Чтобы из единицы вычесть дробь, надо единицу записать в виде неправильной дроби со знаменателем, равным знаменателю дроби, которую вычитаем. Произведение двух дробей есть дробь, в числителе которой произведение знаменателей, а в знаменателе - произведение числителей. При умножении целого числа на дробь,целое число надо записать в виде дроби со знаменателем один. Чтобы разделить дробь на дробь, надо делимое умножить на число, обратное делителю. Два числа называются взаимно обратными, если их частное равно единице. тест
- Урок был полезен для меня, я понимал все, о чем говорилось и что делалось на уроке. - Урок был интересен, в определенной степени полезен для меня, мне было на уроке достаточно комфортно. - Я понял о чем шла речь на уроке, но мне следует получить консультацию у учителя.
Домашнее задание
