Урок-презентация по математике 5 класс «Обыкновенные дроби»
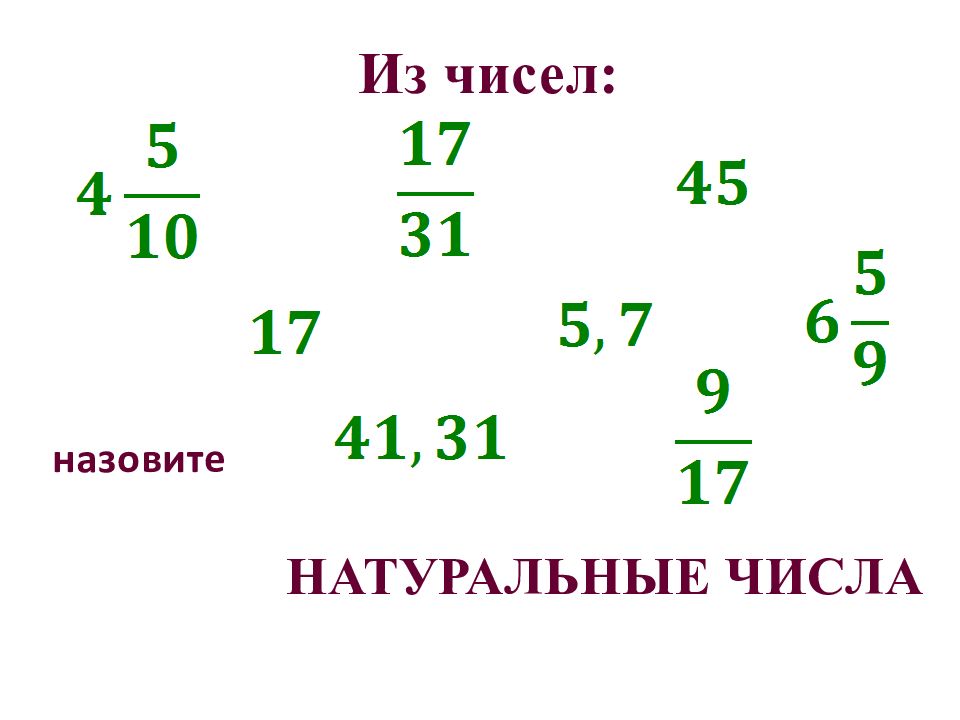
Темы: Урок 1 «Доли» и «Что такое дробь» Урок 2 «Основное свойство дроби» и «Приведение дробей к общему знаменателю» Урок 3 «Сравнение дробей » и «Сложение дробей» Урок 4 «Вычитание, умножение и деление дробей» 2 Обыкновенные дроби
Урок 1 Доли Мама купила арбуз и разрезала его на 6 равных частей: бабушке, дедушке, папе, маме, двум детям. Эти равные части называют долями, так как арбуз разделили на 6 равных частей, каждый получил одну шестую арбуза, записывается это так 3 Обыкновенные дроби
Что такое дробь 4 Обыкновенные дроби Прямоугольник разделён на 3 равные части, две третьих этого прямоугольника закрашено. Для обозначения такой записи используют специальную «двухэтажную» запись Такую запись называют дробью.
Число внизу, под чертой, показывает на сколько равных частей делили. Его называют знаменателем. Число вверху, над чертой, показывает сколько таких частей взяли. Его называют числителем дроби. Обыкновенные дроби 5
Дробь, числитель которой меньше знаменателя, называют правильной. Дробь, числитель которой больше знаменателя или равен ему, называют неправильной. Обыкновенные дроби 6
Закрепим: Круг разделили на 6 равных частей, каждая часть составляет круга. Сколько частей круга закрашено? Какая часть квадрата закрашена? Обыкновенные дроби 7
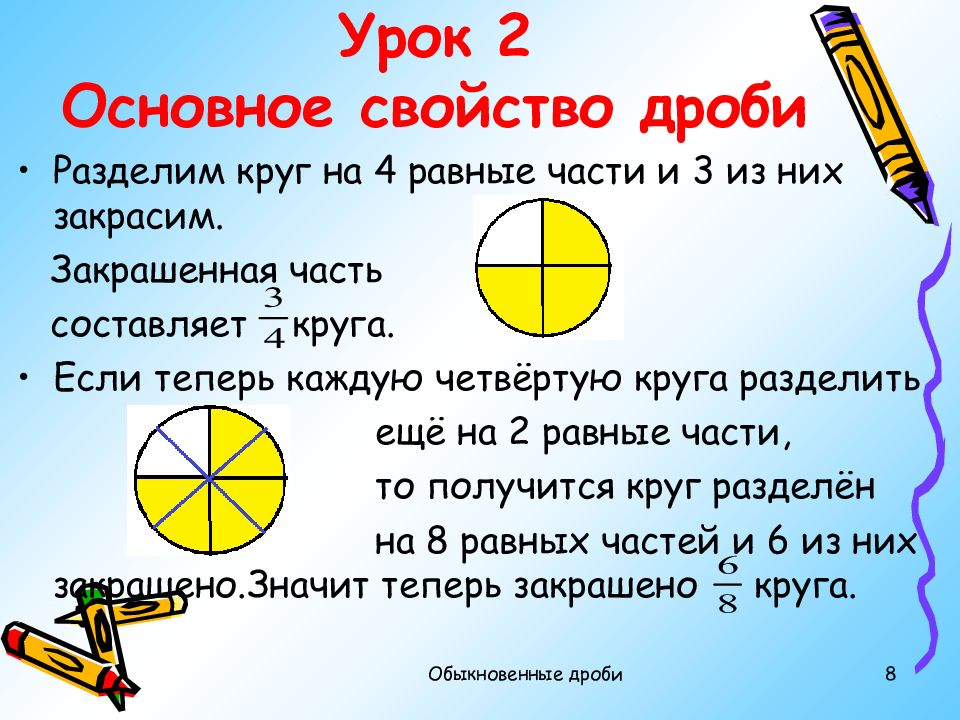
Урок 2 Основное свойство дроби 8 Обыкновенные дроби Разделим круг на 4 равные части и 3 из них закрасим. Закрашенная часть составляет круга. Если теперь каждую четвёртую круга разделить ещё на 2 равные части, то получится круг разделён на 8 равных частей и 6 из них закрашено.Значит теперь закрашено круга.
В обоих случаях закрашена одна и та же часть круга, а значит дроби выражают одну и ту же величину. Такие дроби называются равными. ЗАПОМНИТЕ: Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Что бы сократить дробь, её числитель и знаменатель нужно разделить на их общий делитель. 9 Обыкновенные дроби
10 Обыкновенные дроби Приведение дробей к общему знаменателю При решение задач дроби, имеющие разные знаменатели приходится заменять равными им дробями с одинаковыми знаменателями, при этом стараются подобрать наименьший общий знаменатель.
Например, приведём к общему знаменателю дроби. Больший знаменатель - число 24 - делится на меньший, поэтому его можно взять его в качестве общего знаменателя данных дробей. Теперь нужно привести дробь к знаменателю 24. Найдём дополнительный множитель 24:8=3. Значит, Обыкновенные дроби
12 Обыкновенные дроби ВАЖНО! в качестве общего знаменателя дробей всегда можно взять произведение их знаменателей ЗАКРЕПИМ Приведите к общему знаменателю дроби: = ; = = ; = В начало
13 Обыкновенные дроби Урок 3 Сравнение дробей Сравнить 2 неравные дроби- это значит установить, какая из них больше, а какая- меньше. Если разделим яблоко на 5 равных долей, то 2 доли составят меньшую часть яблока, чем 3 такие же доли. Значит <
14 Обыкновенные дроби Рассмотренный пример позволяет сделать вывод : из двух дробей с одинаковым знаменателем больше та, у которой больше числитель, и меньше та, у которой числитель меньше. ВАЖНО! Чтобы сравнивать дроби с разными знаменателями, их сначала нужно привести к общему знаменателю.
15 Обыкновенные дроби Проверим себя: Сравните дроби:
04.07.13 16 Обыкновенные дроби Сложение дробей С дробными числами, как и с натуральными можно выполнять арифметические действия. Рассмотрим сначала сложение дробей
17 Обыкновенные дроби Что бы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежний. Что бы складывать дроби с разными знаменателями их сначала нужно привести к общему знаменателю.
18 Обыкновенные дроби Закрепим Сложите дроби: и) В начало
19 Обыкновенные дроби Урок 4 Вычитание дробей Вычитание дробных чисел, как и натуральных, определяется на основе действий сложения: вычесть из одного числа другое- это значит найти такое число, которое при сложении со вторым даёт первое. Например:
20 Обыкновенные дроби Запомните! Чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним. Важно! Чтобы находить разность дробей с разными знаменателями, их сначала нужно привести к общему знаменателю.
21 Обыкновенные дроби Закрепим Найдите разность:
22 Обыкновенные дроби Умножение дробей Запомните! Что бы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель на знаменатель.
Произведение взаимообратных дробей равно 1. Обыкновенные дроби
Чтобы разделить дробь на дробь, нужно делимое умножить на дробь, обратную делителю. Например, Обыкновенные дроби
Найдите произведение: Выполните деление: В начало Обыкновенные дроби
26 Обыкновенные дроби Спасибо за внимание Презентация создана по учебнику МАТЕМАТИКА 5 класс (под редакцией Г.В. Дорофеева, И.Ф.Шарыгина, 12-е издание Москва « Просвящение »)
