Первый слайд презентации: Механика. Молекулярная физика. Термодинамика
Лекция 4. Неинерциальные системы. Силы инерции Сила упругости
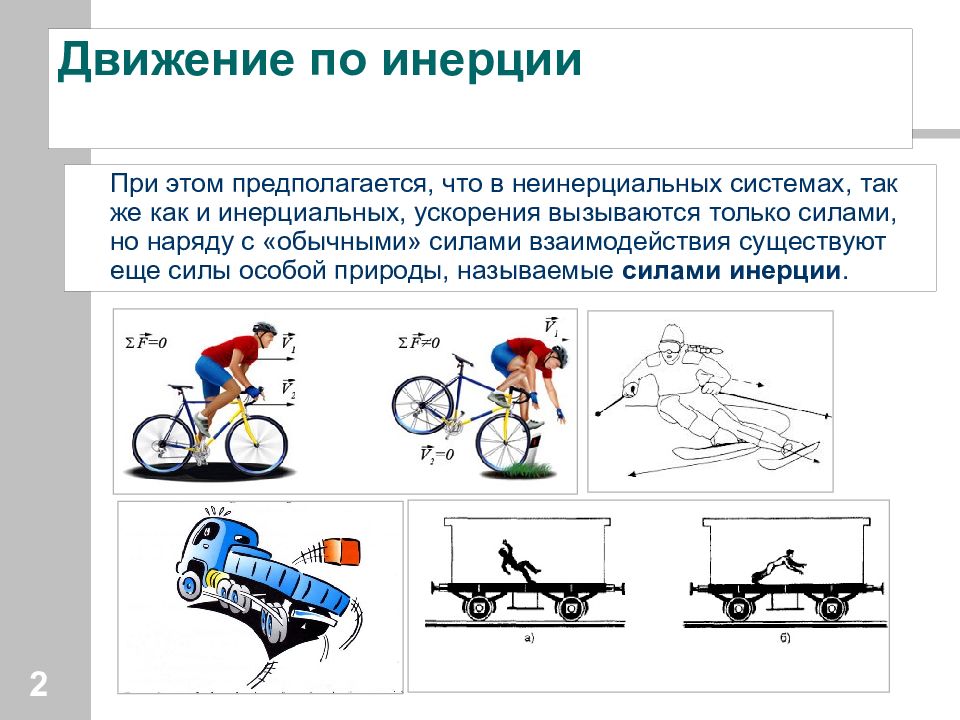
Слайд 2: Движение по инерции
При этом предполагается, что в неинерциальных системах, так же как и инерциальных, ускорения вызываются только силами, но наряду с «обычными» силами взаимодействия существуют еще силы особой природы, называемые силами инерции. 2
Слайд 3: Неинерциальные системы отсчета
3 Неинерциальной системой отсчета называется система, движущаяся ускоренно относительно инерциальной. Ускорение а г материальной точки по отношению к неинерциальной системе отсчета не удовлетворяет второму закону Ньютона, т. е. не равно отношению равнодействующей F всех сил, приложенных к материальной точке со стороны взаимодействующих с ней тел, к массе m этой точки: Иными словами, материальная точка или твердое тело могут изменять состояние своего движения по отношению к неинерциальной системе отсчета без всякого воздействия на них со стороны других тел.
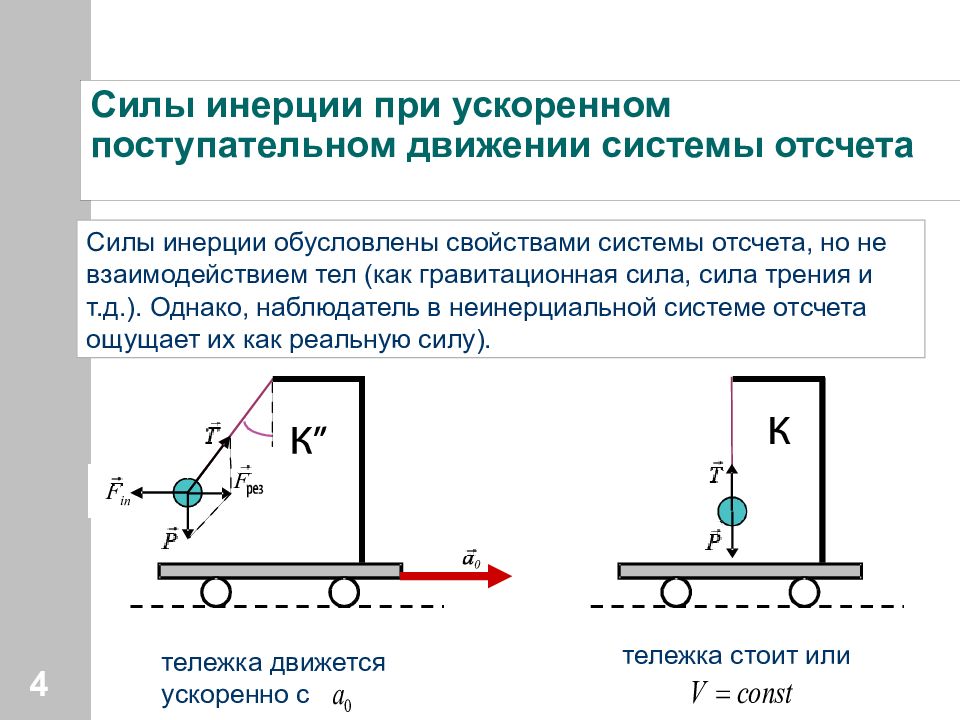
Слайд 4: Силы инерции при ускоренном поступательном движении системы отсчета
тележка движется ускоренно с тележка стоит или Силы инерции обусловлены свойствами системы отсчета, но не взаимодействием тел (как гравитационная сила, сила трения и т.д.). Однако, наблюдатель в неинерциальной системе отсчета ощущает их как реальную силу). 4
Слайд 5: Силы инерции при ускоренном поступательном движении системы отсчета
В К:, равновесие, v=const (V=0) В К ” : Если тележка движется поступательно, с ускорением, то нить отклоняется на угол так, чтобы результирующая сил была уравновешена силой инерции. Наступает равновесие, т.е. 5 В системе К ” используются те же уравнения динамики, что и в К, но формально добавляется сила инерции поступательного движения, равная где m - масса тела, - ускорение системы отсчета. Знак «минус» показывает, что сила инерции направлена противоположно направлению ускорения системы.
Слайд 6: Силы инерции при ускоренном поступательном движении системы отсчета
Если грузу, сообщить ускорение а ' относительно вагона, то второй закон Ньютона для неинерциальной системы отсчета запишется в виде : где а ' — ускорение тела в неинерциальной системе отсчета; ∑ F — сила (или их равнодействующая), обусловленная воздействием тел друг на друга; F in = -т а 0 — сила инерции, обусловленная ускоренным поступательным движением системы отсчета. Особенностью рассмотренной силы инерции является то, что она обусловлена не действием других тел (как, на пример, упругие силы, силы трения и т. д.), а ускоренным поступательным движением системы отсчета. Эти силы часто называют фиктивными. 6
Слайд 7: Движение во вращающейся системе отсчета
Рассмотрим движение во вращающейся системе отсчета. Система K ' (карусель) вращается относительно системы K с постоянной угловой скоростью ω = const вокруг неподвижной в системе К оси z. Человек перемещается по движущейся карусели. Z X Y 0 K условно неподвижная система K’ неинерциальная система (карусель) ω 7
Слайд 8: Движение во вращающейся системе отсчета
Совместим начала отсчета обеих систем так, чтобы в некоторый момент времени t радиус-векторы частицы в них совпали. Тогда за последующее время dt частица переместится в системе K ' на v ' dt, а вместе с системой K ' еще и повернется относительно неподвижной системы на угол d , тогда суммарное перемещение: Движение во вращающейся системе отсчета Разделив это выражение на dt, получим закон преобразования скоростей: ( * )
Слайд 9: Формулы преобразования скоростей и ускорений
найдем приращение скорости ( так как ω = const) : Но изменение v ' происходит как в результате движения частицы с ускорением a ' в системе K ', так и поворота вектора скорости v ' вместе с системой K ' относительно системы K 9 ( * * ) ( *** ) Подставляя в (**) выражения v’ и dr, получаем: Разделив полученное выражение на dt и приведя подобные выражения, найдем закон преобразования ускорений:
Слайд 10: Формулы преобразования скоростей и ускорений
Центростремительным или осестремтельное ускорение Кориолисово ускорение (по имени Гюстава Кориолиса) 10 Последнее слагаемое в формуле направлено по радиусу к оси вращения и поэтому называется центростремительным или осестреми- тельным ускорением
Слайд 11: Формулы преобразования скоростей и ускорений
Если система K ' относительно системы K совершает поступательное и вращательное движение одновременно добавляется еще ускорение поступательного движения: Используя формулу преобразования ускорений, запишем закон движения так, чтобы он выполнялся и в неинерциальной системе отсчета (2-ой з-н Ньютона для неинерциальной системы отсчета): где R – вектор, проведенный к частице от оси вращения Формулы преобразования скоростей и ускорений R 11
Слайд 12: Силы инерции
Силы инерции отличаются от "обычных" сил тем, что они обусловлены не взаимодействием тел, а ускоренным движением системы отсчета. Они существуют только в неинерциальных системах отсчета и направлены противоположно ускорению системы! Чтобы записать уравнение движения в неинерциальной системе отсчета, следует к векторной сумме "обычных" сил F i добавить силы инерции: 12
Слайд 13: Центробежная сила инерции
Z’’ Y’’ X’’ K’’ m,r Диск вращается с вместе с шариком на пружине и на спице. В К ” : шарик покоится! Это значит, что кроме силы, действующей со стороны пружины к шарику приложена центробежная сила инерции: 13 Формально две силы действуют на шарик, и результирующая =0. Центробежная сила инерции - сила действует на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе или движется относительно нее со скоростью v '.
Слайд 14: Центробежная сила инерции
Так как мы живем на вращающейся Земле, то роль центробежной и кориолисовой сил может оказаться существенной. То, что мы обычно называем силой тяжести, является результирующей двух сил – гравитационной и центробежной: Отсюда следует, что ускорение свободного падения зависит от географической широты места наблюдения. 14
Слайд 15: Центробежная сила инерции
Согласно теореме косинусов Т.к. где R з – радиус Земли, то с точностью до малых первого порядка получим: Центробежная сила инерции 15
Слайд 16: Сила Кориолиса
При движении тела в «К ” » кроме центробежной силы инерции появляется еще одна сила инерции – Кориолисова сила, которую можно обнаружить, т.к. она реально существует. Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. 16
Слайд 17: Сила Кориолиса
Диск стоит, шарик катится точно по радиусу Диск вращается – траектория шарика такая, как если бы на него действовала сила к скорости. Это и есть сила Кориолиса. Она меняет направление скорости, но не величину. Вектор F K перпендикулярен векторам скорости v ' тела и угловой скорости вращения ω системы отсчета в соответствии с правилом правого винта. 17
Слайд 18: Силы инерции
При движении по Земле со скоростью v '=5км / час на пешехода с массой m = 60 кг действует очень малая кориолисова сила. Ее максимальная величина F кор =2 m ω v '≈0,012 Н. Но в летящем со скоростью v ' = 1000 км/час самолете эта сила, толкающая человека в бок, составляет 2,4 Н. Пассаты (ветры, дующие от тропиков к экватору) в обоих полушариях будут отклоняться к западу, а текущие реки будут отклоняться в се- верном полушарии к правому берегу, а в южном – к левому. 18 В северном полушарии сила Кориолиса подмывает правый берег рек, в Южном – левый.
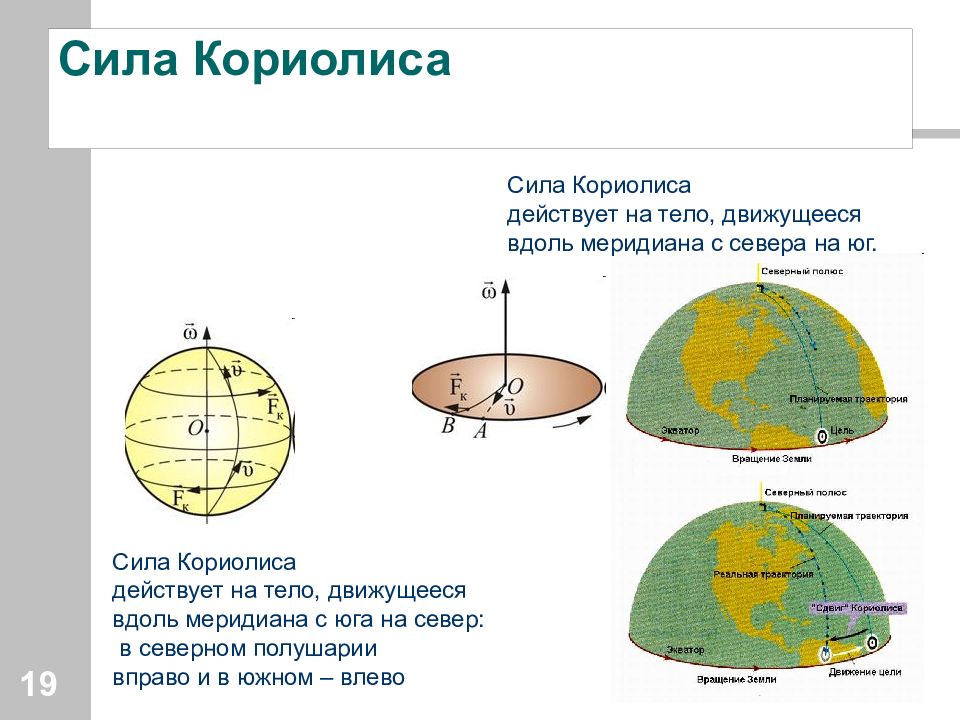
Слайд 19: Сила Кориолиса
19 Сила Кориолиса действует на тело, движущееся вдоль меридиана с юга на север: в северном полушарии вправо и в южном – влево Сила Кориолиса действует на тело, движущееся вдоль меридиана с севера на юг.
Слайд 20: Сила Кориолиса
Благодаря силе Кориолиса падающие на поверхность Земли тела отклоняются к востоку (на широте 60 о это отклонение должно составлять 1 см при падении с высоты 100 м). С силой Кориолиса связано поведение маятника Фуко, явившееся в свое время одним из доказательств вращения Земли. Если бы этой силы не было, то плоскость колебаний качающегося вблизи поверхности Земли маятника оставалась бы неизменной (относительно Земли). Действие же сил Кориолиса приводит к вращению плоскости колебаний вокруг вертикального направления. 20 ЗНАМЕНИТЫЙ ОПЫТ ФУКО, проведенный в Пантеоне в Париже в 1851, который продемонстрировал, что Земля вращается вокруг своей оси. Маятник представлял собой груз весом 28 кг, подвешенный под куполом здания на проволоке длиной 67 м.
Слайд 21: Сила Кориолиса
На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки. 21 Наблюдатель, находящийся на Земле и вращающийся вместе с нею, находится в неинерциальной (вращающейся) системе отсчёта и будет видеть, что плоскость колебаний маятника медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли.
Слайд 22: Сила Кориолиса
Как следует из рисунка, плоскость качаний маятника поворачивается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентрической системы отсчета дело обстоит так: плоскость качаний остается неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот. Если тело удаляется от оси вращения, то сила F k направлена противоположно вращению и замедляет его. Если тело приближается к оси вращения, то F k направлена в сторону вращения.
Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу. Для любого из тел, находящихся в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. 23
Слайд 25
Силы упругости Деформация называется упругой, если с прекращением действия приложенных сил, деформация исчезает. Тело принимает первоначальный объем или форму под действием внутренних упругих сил. Природа внутренних сил определяются совокупностью механических, электрических и тепловых свойств тела (или вещества). Формула для упругой силы: где х – смещение от положения равновесия, к – коэффициент Деформация называется пластической, если с прекращением действия приложенных сил, она не исчезает полностью (сохраняется «остаточная деформация»).
Слайд 26: Силы упругости
Важнейшие виды деформации: продольное растяжение и сжатие всестороннее растяжение и сжатие сдвиг кручение поперечный и продольный изгибы Все эти деформации можно свести к продольному растяжению и сжатию (в 2-х направлениях) и сдвигу.
Слайд 27: Силы упругости
Рассмотрим продольное растяжение. Относительная деформация – это отношение абсолютной деформации х к длине стержня х: Усилие – величина внешней силы, действующей на единицу площади перпендикулярно к ней.
Слайд 28: Силы упругости
Итак, под действием внешней силы возникает деформация тела и появляются упругие силы (внутренние). Величина упругой силы на единицу поверхности называется «напряжением». Усилие и напряжение противоположны друг другу. В 1675 году Роберт Гук установил закон (Закон Гука): Е- модуль Юнга, 1/Е= - коэффициент упругости
Слайд 29: Силы упругости
Модуль Юнга численно равен усилию, когда тело растянуто вдвое, т.к. х=х, что не реально. При продольном растяжении наблюдается поперечное сжатие. Относительное сжатие d / d с относительным удлинением связано через коэффициент Пуассона : а з-н Гука запишется: где d – толщина стержня, а d – изменение толщины.
Слайд 30: Силы упругости
Деформация сдвига x x A B A’ B’ Деформацией сдвига называется такая деформация, при которой все слои тела, параллельные данной плоскости не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. AA’= x – абсолютный сдвиг, - угол сдвига Усилие
Слайд 31: Силы упругости
Тогда закон Гука для сдвига запишется: где G – модуль сдвига, численно равен усилию при tg =1 ( при малых углах!) Закон Гука для сдвига
Слайд 32: Силы упругости
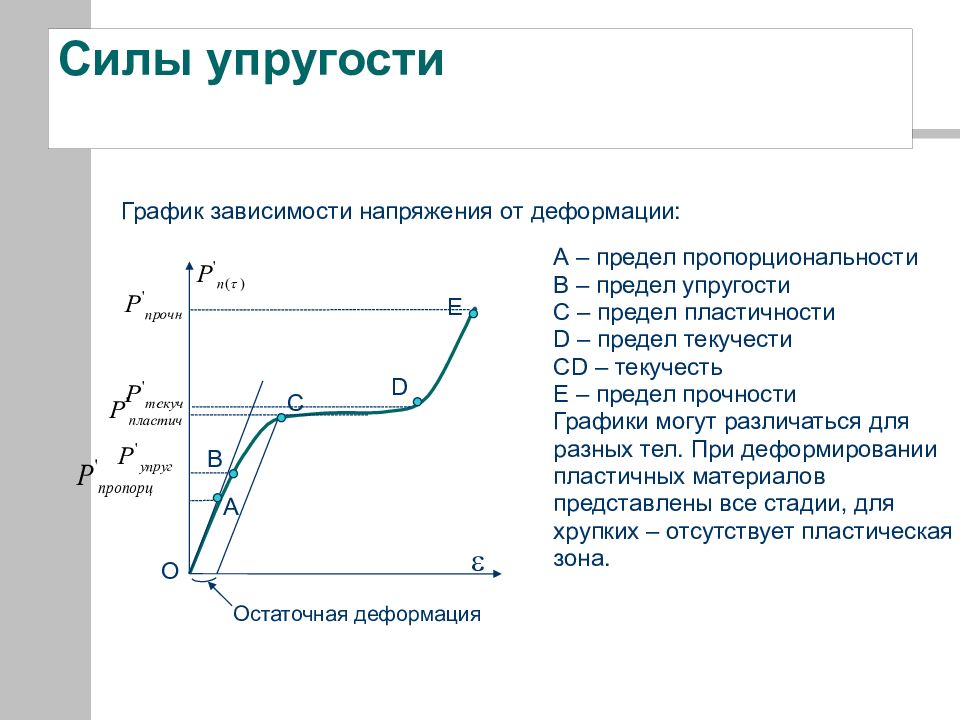
График зависимости напряжения от деформации: A В С D E Остаточная деформация А – предел пропорциональности В – предел упругости С – предел пластичности D – предел текучести С D – текучесть Е – предел прочности Графики могут различаться для разных тел. При деформировании пластичных материалов представлены все стадии, для хрупких – отсутствует пластическая зона. О