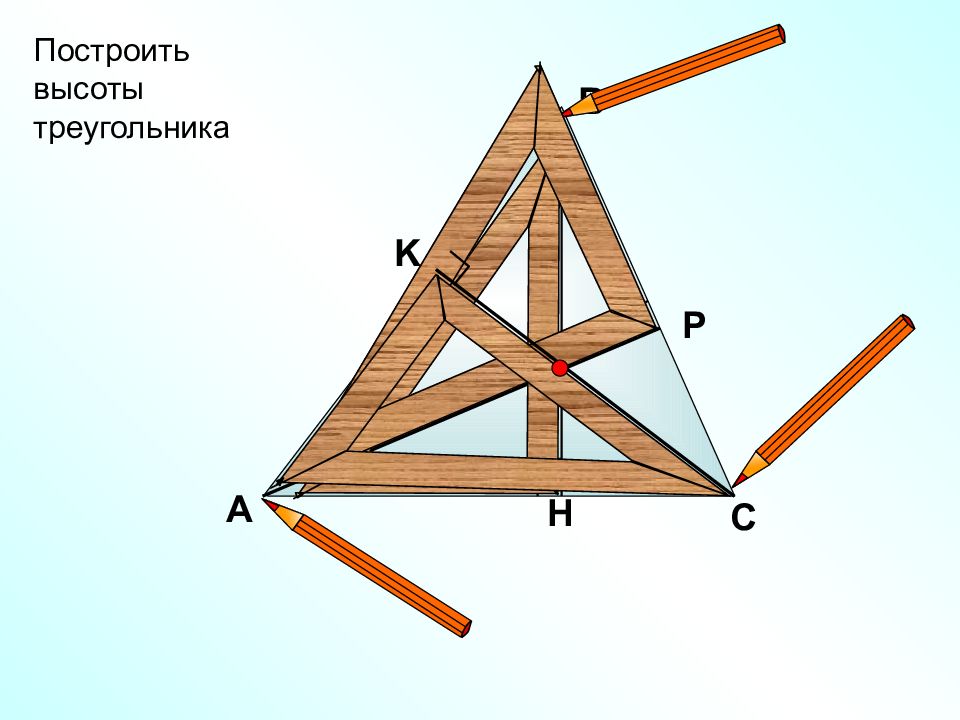
Первый слайд презентации
Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманской обл. Площадь Геометрия 8 класс треугольника
Слайд 2
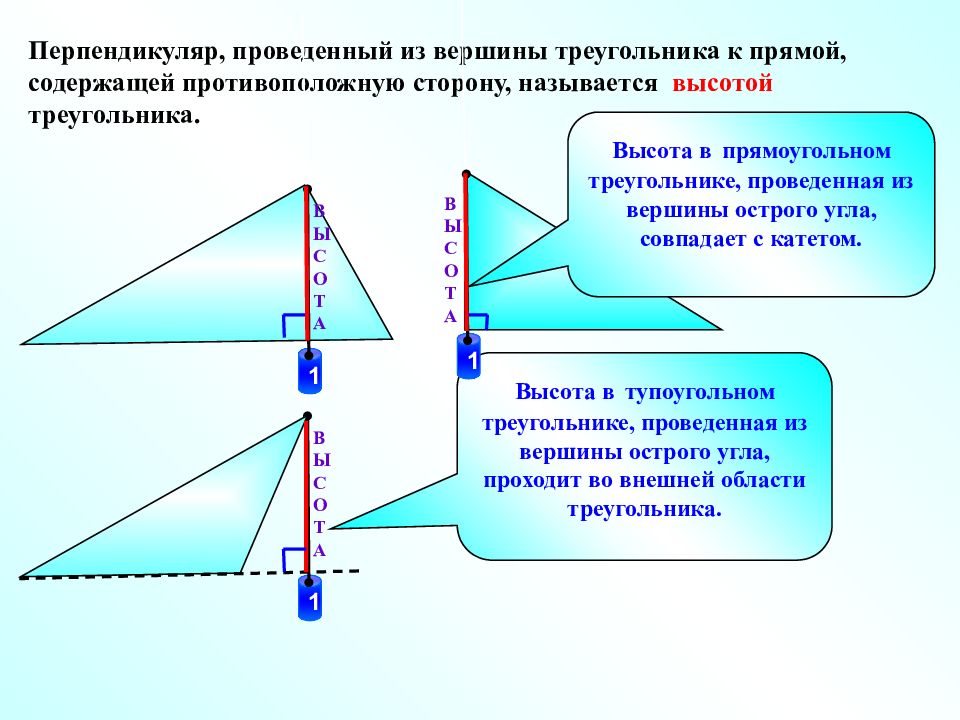
1 Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. В Ы С О Т А В Ы С О Т А Высота в прямоугольном треугольнике, проведенная из вершины острого угла, совпадает с катетом. Высота в тупоугольном треугольнике, проведенная из вершины острого угла, проходит во внешней области треугольника. В Ы С О Т А 1 1
Слайд 3
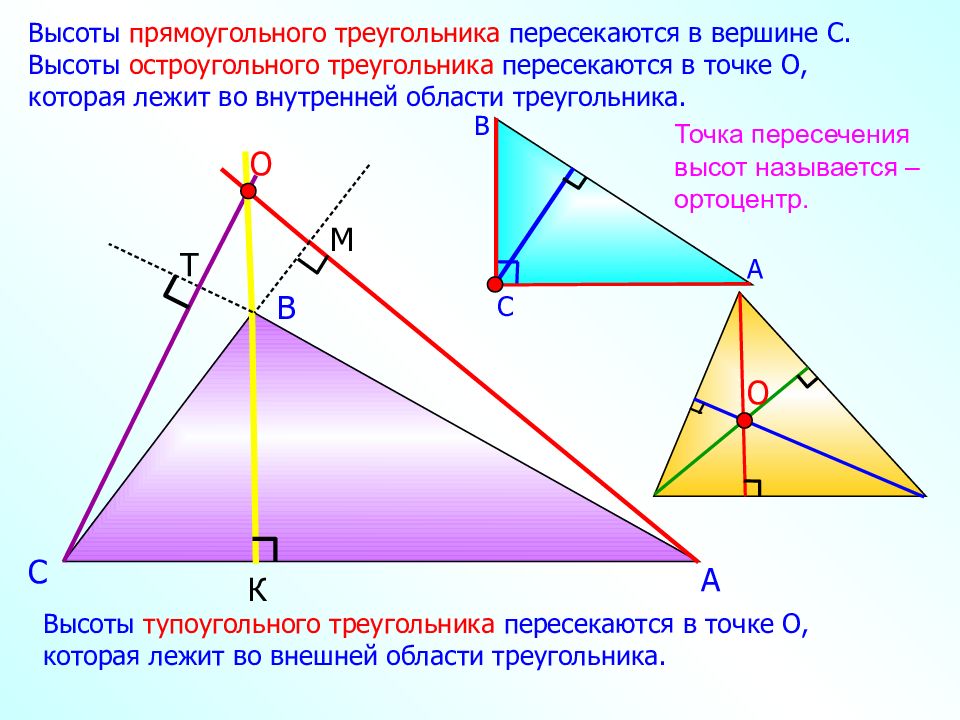
А В С К М O Т Высоты тупоугольного треугольника пересекаются в точке О, которая лежит во внешней области треугольника. Высоты прямоугольного треугольника пересекаются в вершине С. Высоты остроугольного треугольника пересекаются в точке О, которая лежит во внутренней области треугольника. O А В С Точка пересечения высот называется – ортоцентр.
Слайд 4
Свойства площадей 1 0. Равные многоугольники имеют равные площади. 2 0. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Эти свойства помогут нам получить формулу для вычисления площади параллелограмма.
Слайд 5
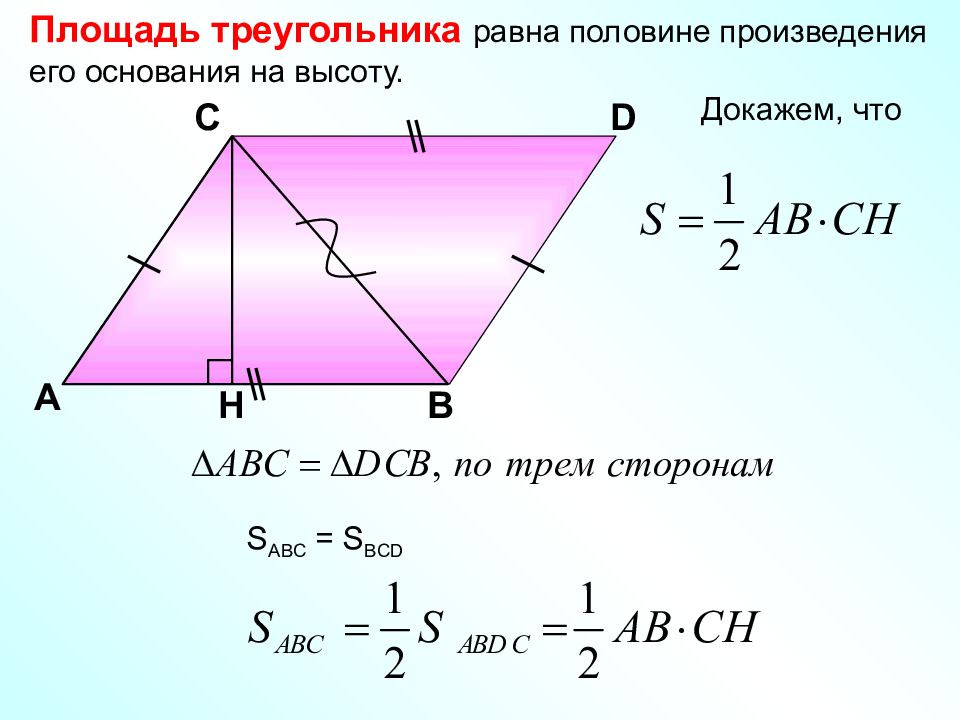
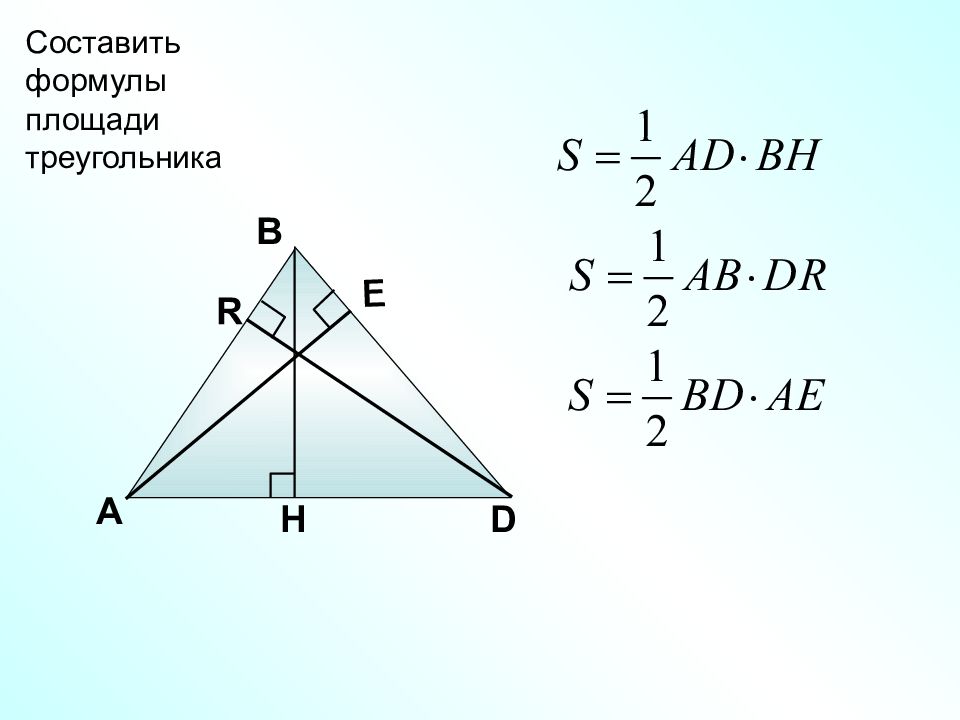
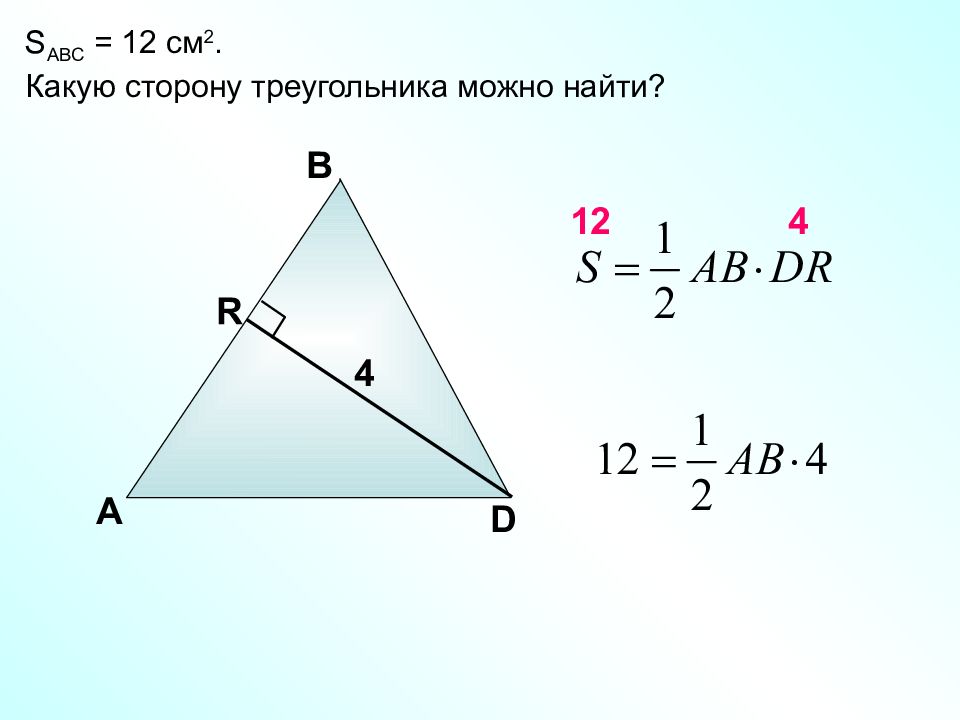
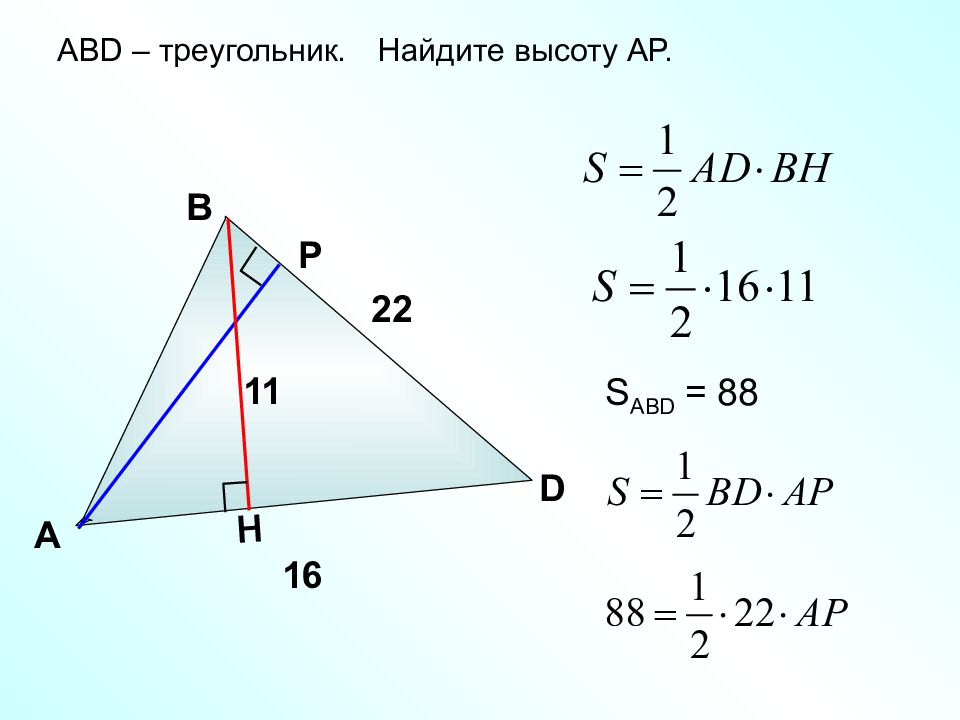
Площадь треугольника равна половине произведения его основания на высоту. Докажем, что А С D В H S ABC = S BCD
Слайд 8
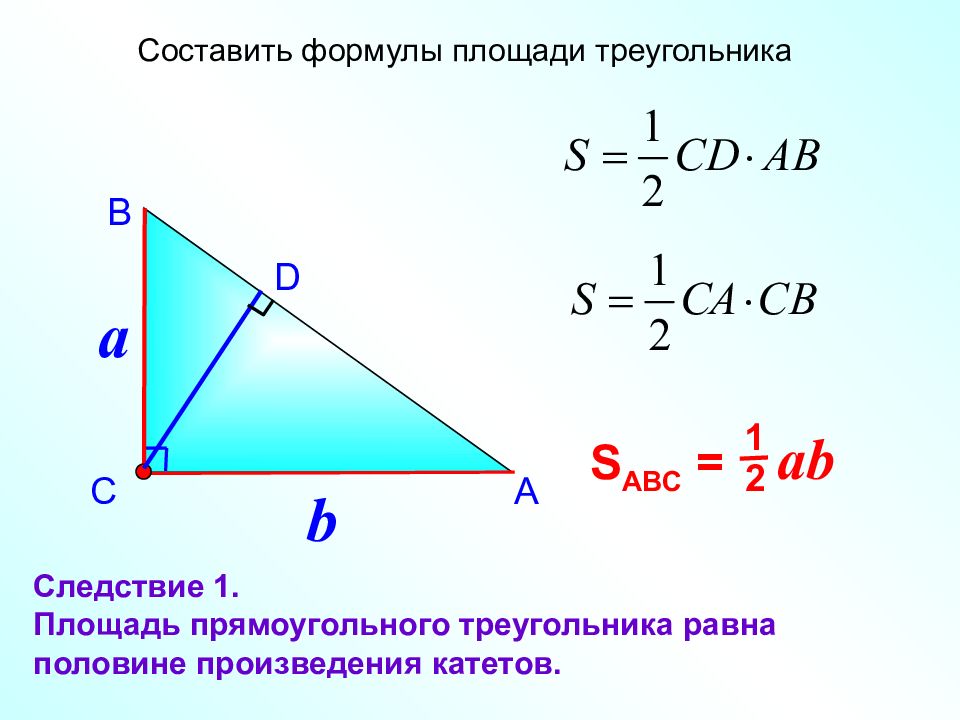
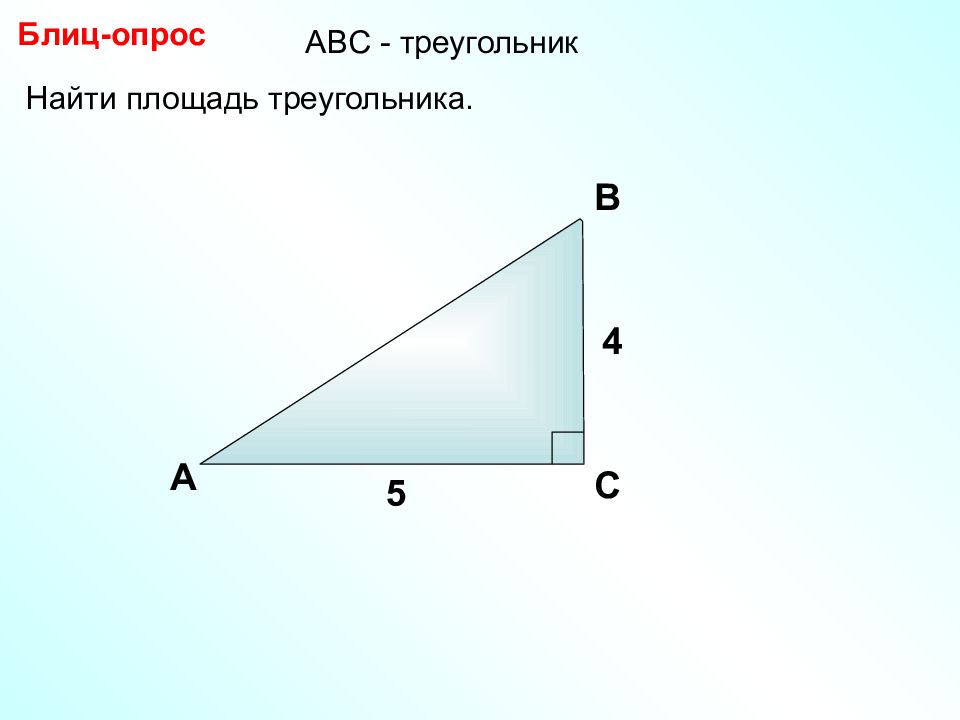
А В С Составить формулы площади треугольника D Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов. a b 1 2 S ABC = ab
Слайд 14
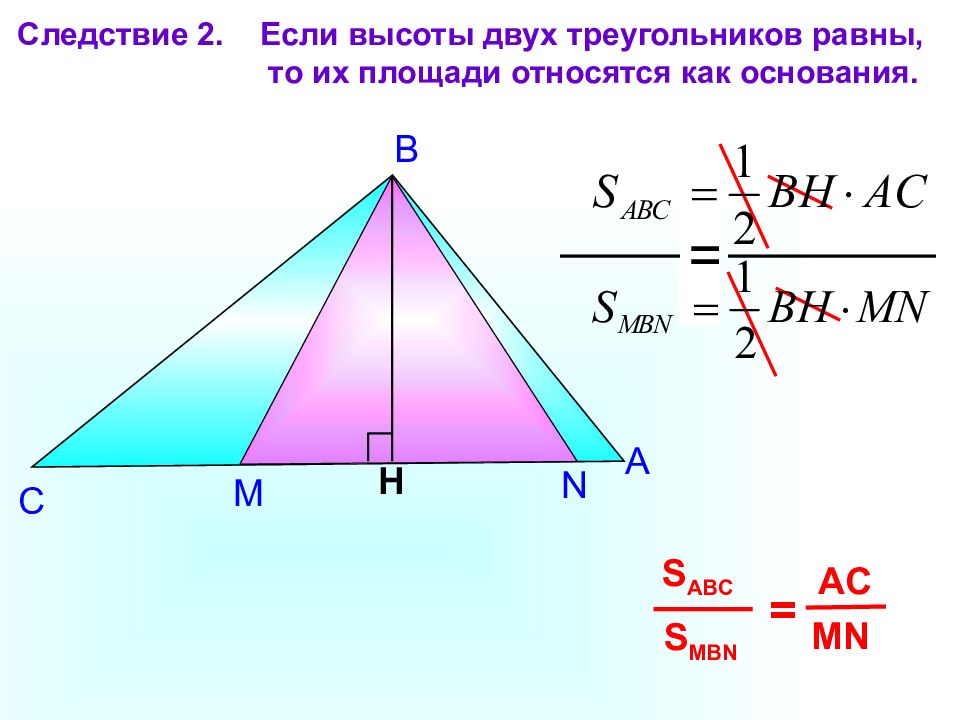
М N А В С Следствие 2. Если высоты двух треугольников равны, то их площади относятся как основания. H S MBN S ABC = MN AC =
Слайд 15
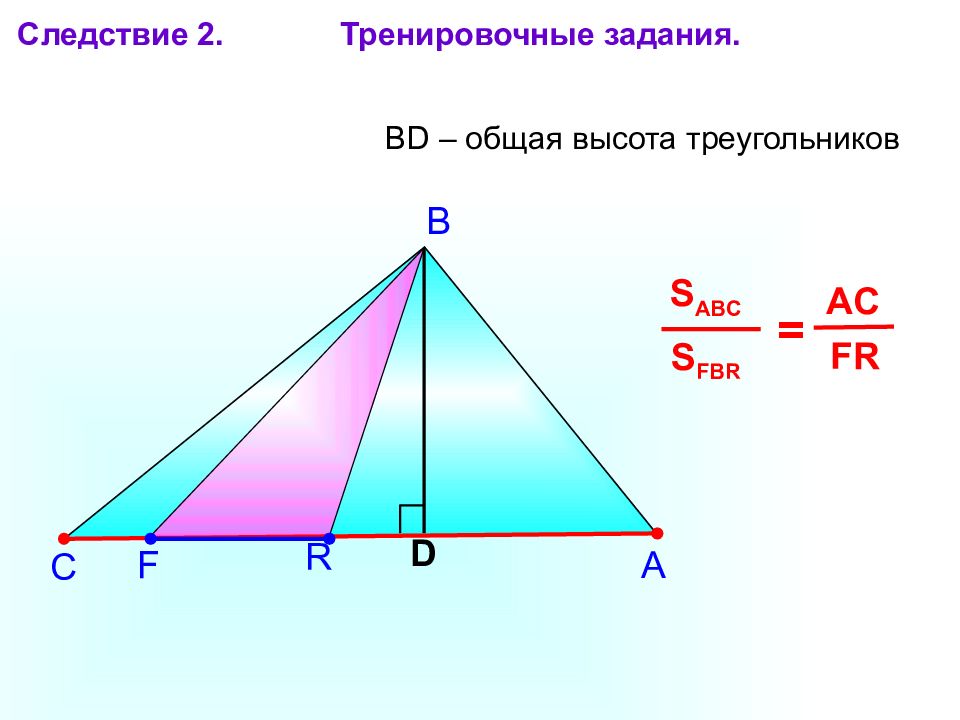
F R А В С Следствие 2. Тренировочные задания. D S FBR S ABC = FR AC BD – общая высота треугольников
Слайд 16
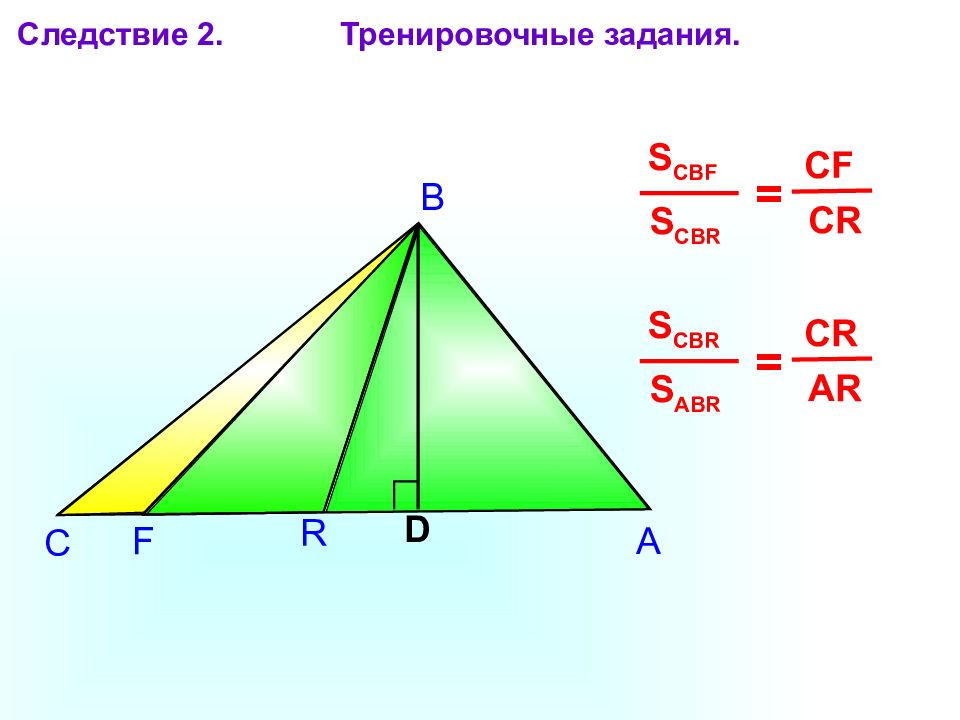
F R А В С Следствие 2. Тренировочные задания. D S CBR S CBF = CR CF S ABR S CBR = AR CR
Слайд 17
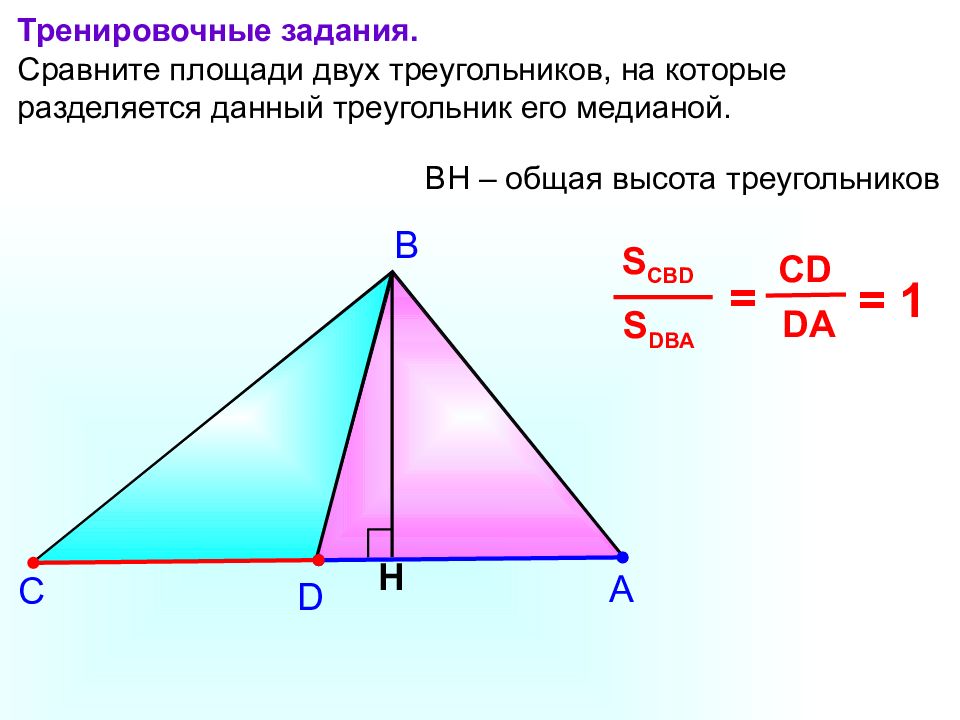
А В С Тренировочные задания. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой. H S DBA S CBD = DA CD D BH – общая высота треугольников = 1
Слайд 18
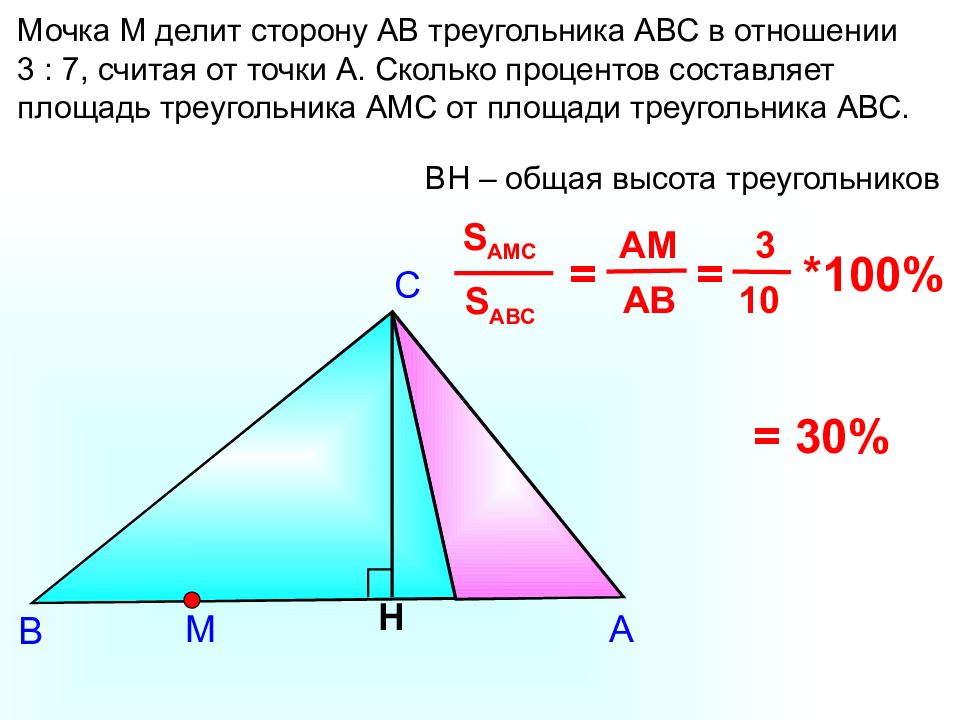
А С В Мочка М делит сторону АВ треугольника АВС в отношении 3 : 7, считая от точки А. Сколько процентов составляет площадь треугольника АМС от площади треугольника АВС. H S A ВС S АМ C = АВ АМ BH – общая высота треугольников = 30% М = *100% 10 3
Слайд 19
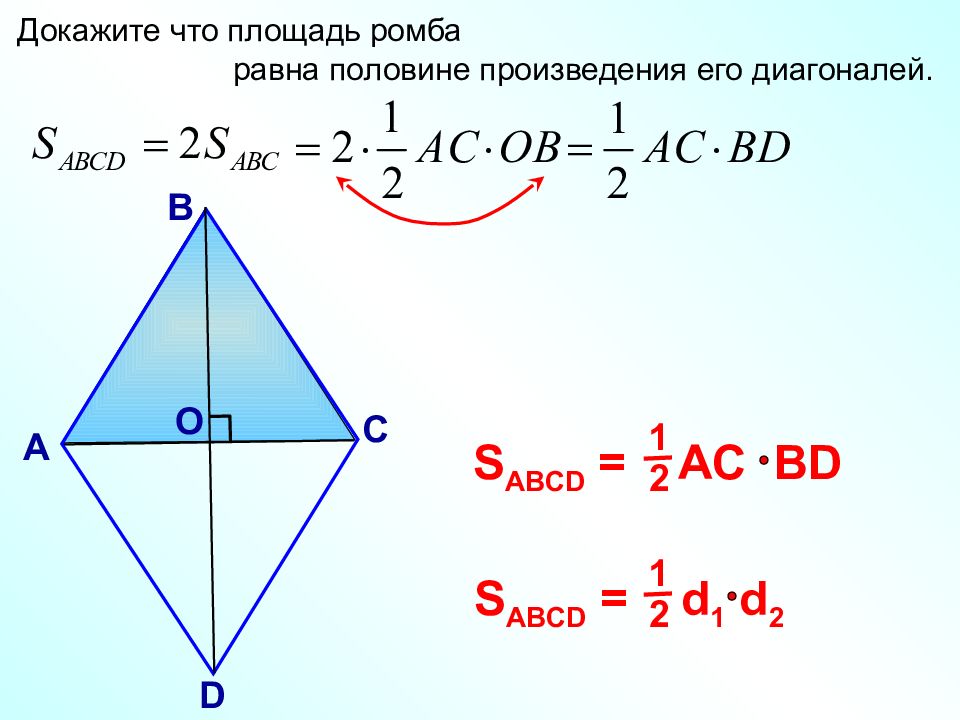
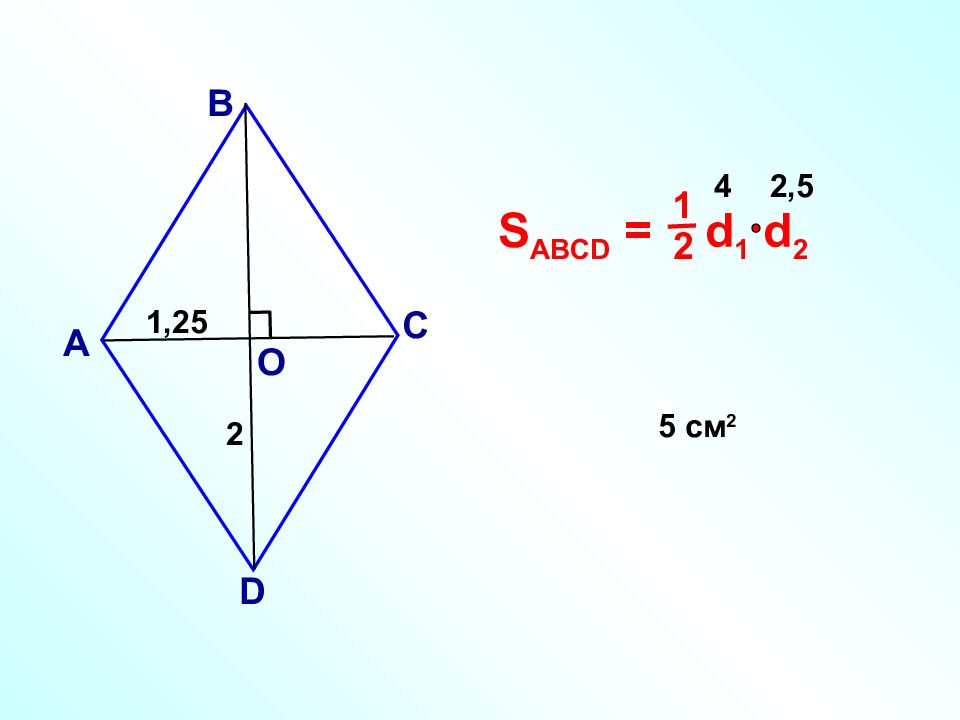
А В С D О Докажите что площадь ромба равна половине произведения его диагоналей. 1 2 S ABCD = AC BD S ABCD = d 1 d 2 1 2
Слайд 21
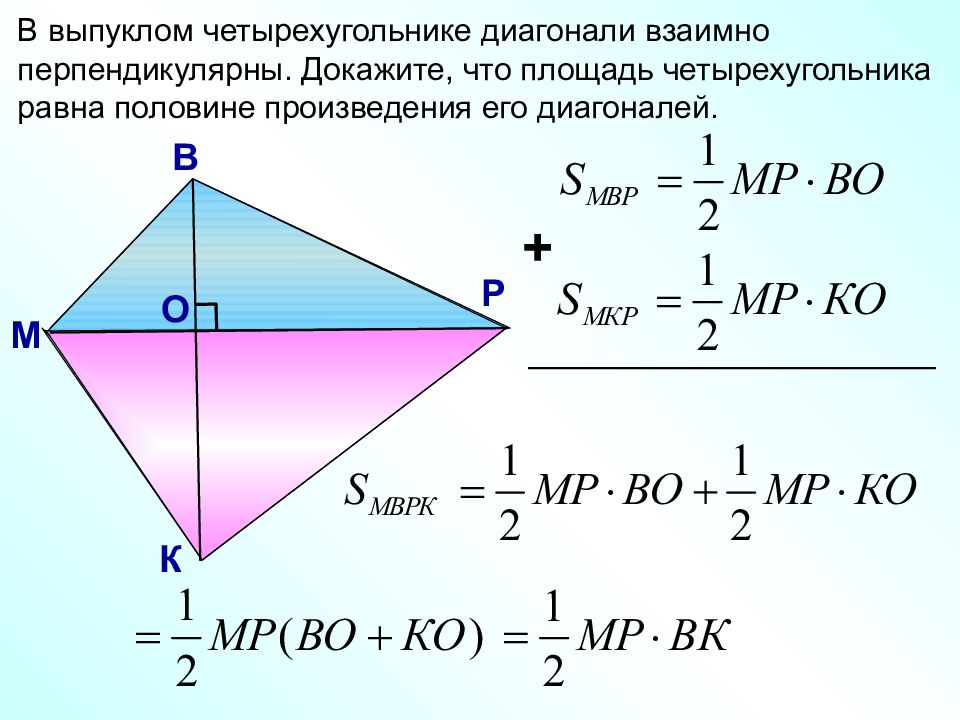
М В Р К О В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырехугольника равна половине произведения его диагоналей. +
Слайд 22
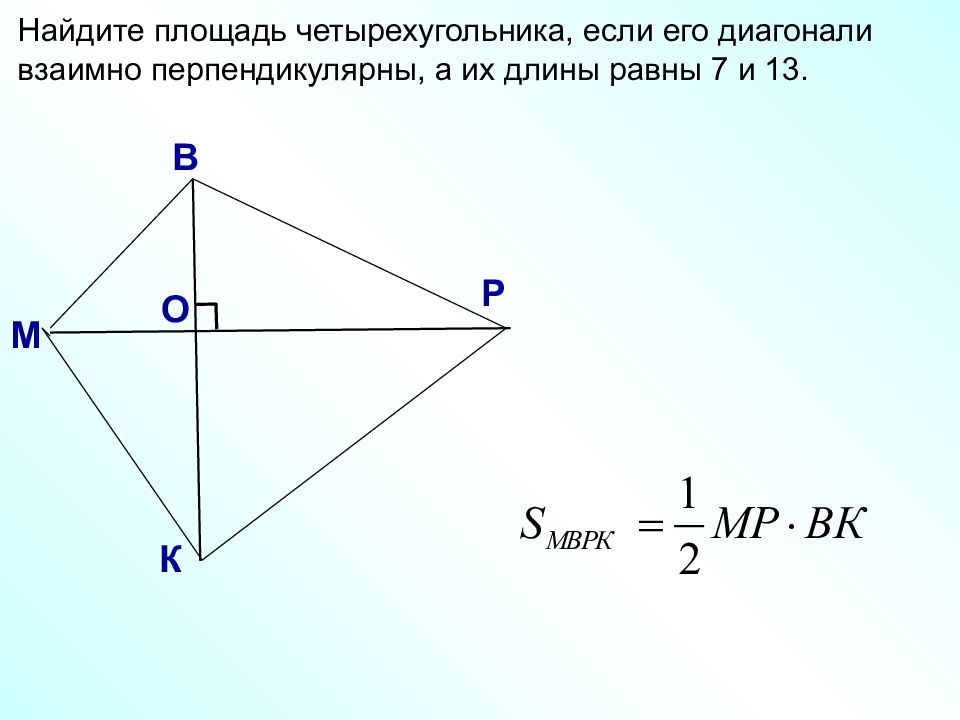
М В Р К О Найдите площадь четырехугольника, если его диагонали взаимно перпендикулярны, а их длины равны 7 и 13.
Слайд 23
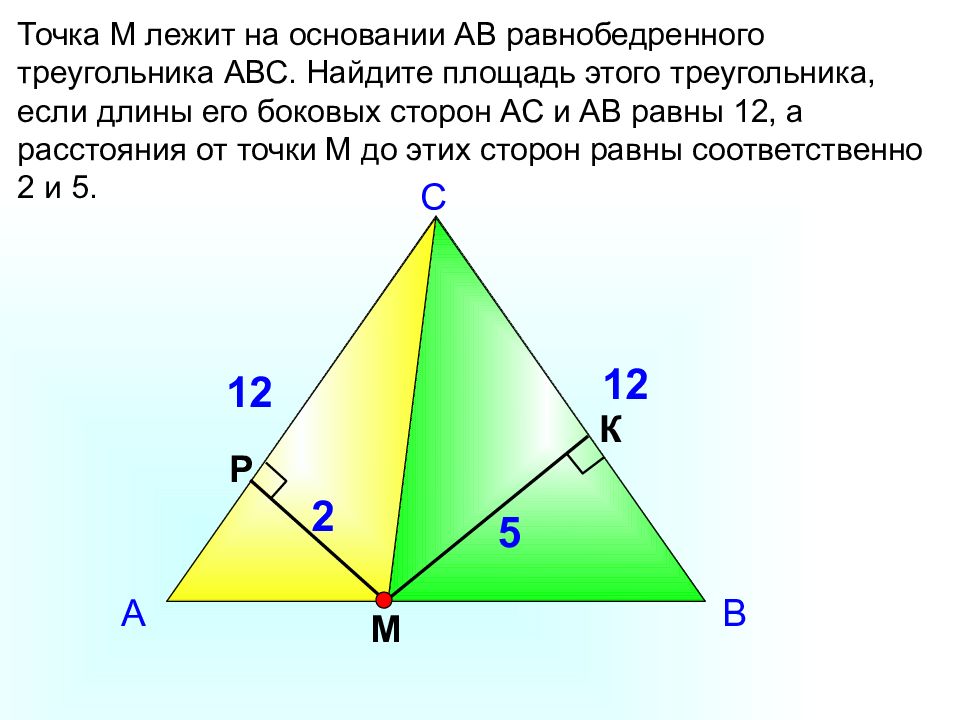
Точка М лежит на основании АВ равнобедренного треугольника АВС. Найдите площадь этого треугольника, если длины его боковых сторон АС и АВ равны 12, а расстояния от точки М до этих сторон равны соответственно 2 и 5. А С В М 12 12 2 Р 5 К
Слайд 24
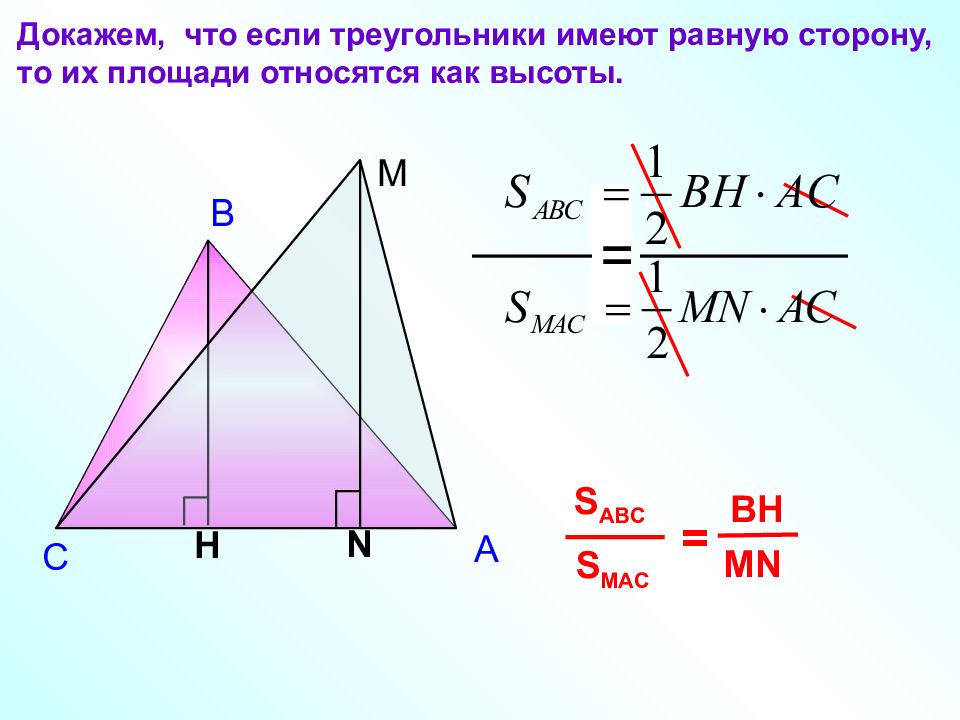
В С Докажем, что если треугольники имеют равную сторону, то их площади относятся как высоты. H S MAC S ABC = MN BH = М N A
Последний слайд презентации: Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори,
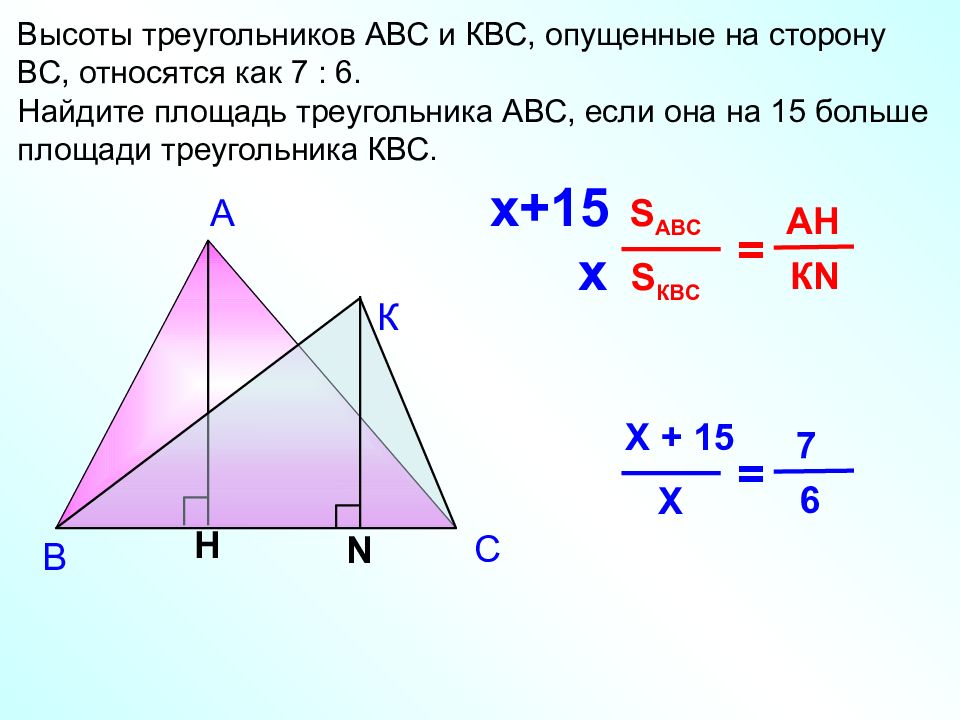
А В Высоты треугольников АВС и КВС, опущенные на сторону ВС, относятся как 7 : 6. Найдите площадь треугольника АВС, если она на 15 больше площади треугольника КВС. H S КВ C S ABC = К N А H К N С х+15 х Х Х + 15 = 6 7