Национальный исследовательский Томский политехнический университет «Прикладная химическая термодинамика» Смороков Андрей Аркадьевич wolfraum@yandex.ru vk.com/wolfraum1993 1
Опрос 2
Димер триоксида сурьмы ( Sb 4 O 6 ) при увеличении температуры претерпевает изменение кубической кристаллической решетки ( C р = 184 + 132,2 ⋅T ) на орторомбическую ( C р = 228,028 + 16,636 ⋅T - 26,87 ⋅T -2 ) при 879 К с поглощением 13,4 кДж/моль тепла. Последующий нагрев до 928 К приводит к плавлению с поглощением 110,04 кДж/моль энергии. Окончательный нагрев полученной жидкости ( C р = 313,8 ) до 1729 К заканчивается кипением. Как будет выглядеть итоговое уравнение для расчета абсолютной энтропии 10 молей данного вещества при 1279 К, если стандартная энтропия при 298 К равняется 220,9 Дж/(моль ⋅ К)? 2. Приведите фундаментальное уравнение Гиббса для внутренней энергии. 3. Приведите формулировку третьего закона термодинамики. 4. Приведите уравнение состояния газа Ван дер Ваальса. 3
Термодинамические потенциалы Внутренняя энергия и энтропия относятся к классу характеристических функций. Функция называется характеристической, если все термодинамические свойства гомогенной системы могут быть выражены непосредственно через нее и ее частные производные по соответствующим переменным. Эти независимые переменные называют естественными. 4
Термодинамические потенциалы Характеристические функции, по определению, содержат в себе всю термодинамическую информацию о системе. Но не все они одинаково удобны для решения конкретных задач. Так, некоторые из естественных переменных, например, энтропию, нельзя измерять (контролировать) в ходе какого-то процесса. Поэтому встает задача перехода от одних переменных к другим экспериментально измеримым, но с условием сохранения характеристичности самой функции. Такой переход осуществляют с помощью преобразований Лежандра. 5
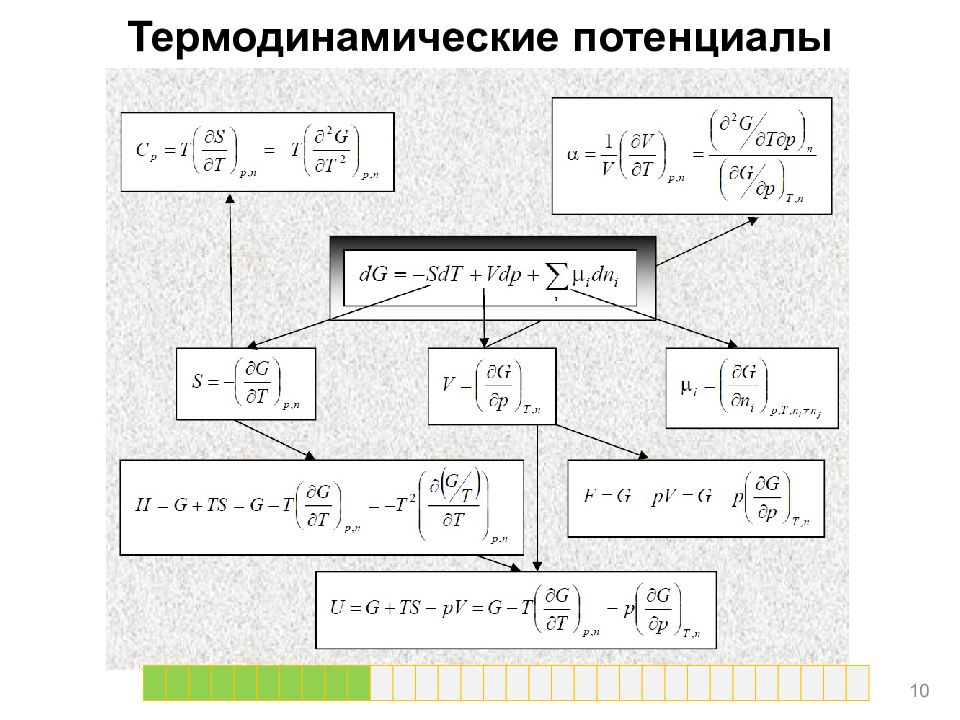
Термодинамические потенциалы С помощью этих преобразований вводятся характеристические функции: • энтальпия: H(S, p, n) = U + pV • энергия Гельмгольца: F(T, V, n ) = U - TS, • энергия Гиббса: G( Т, р, n) = U + pV - TS = Н - TS = F + pV. 6
Термодинамические потенциалы Зависимость термодинамических потенциалов от их естественных переменных описывается фундаментальными уравнениями Гиббса для соответствующей термодинамической функции. В дифференциальной форме эти уравнения получают из уравнений на предыдущем слайде по аналогии с фундаментальным уравнением Гиббса для внутренней энергии. 7
Термодинамические потенциалы 8
Термодинамические потенциалы Химический потенциал характеризует приращение соответствующего термодинамического потенциала при изменении количества данного вещества и постоянстве естественных переменных и количеств остальных веществ. Равенство химических потенциалов веществ является признаком их химического равновесия. Разность химических потенциалов является движущей силой при массопереносе. 9
Термодинамические потенциалы 1 0
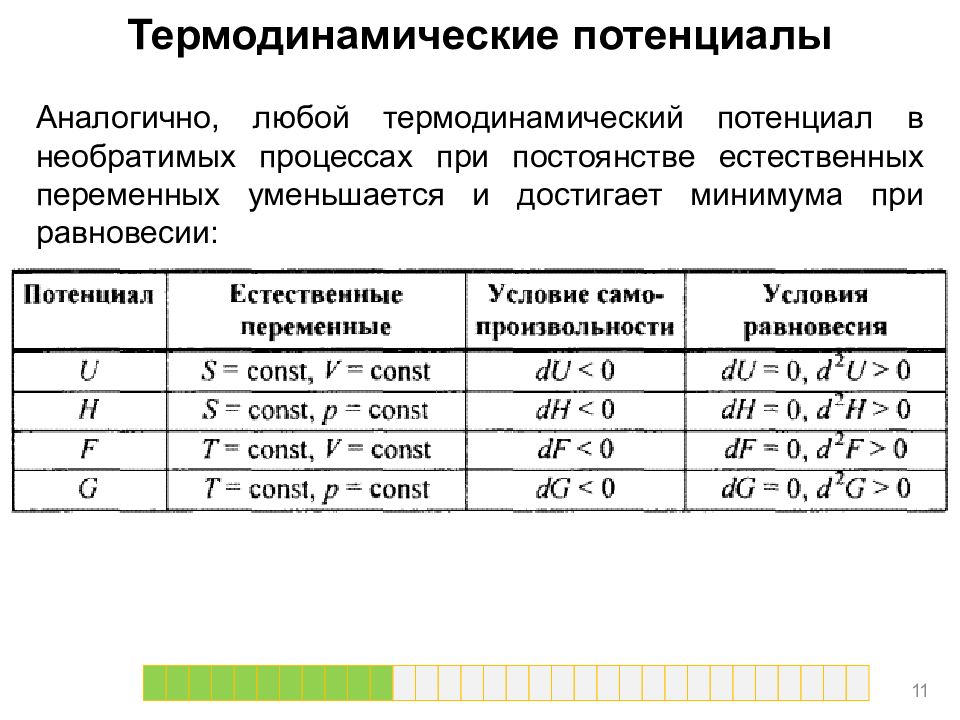
Термодинамические потенциалы Аналогично, любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии: 1 1
Термодинамические потенциалы Наибольшее значение в практических термодинамических расчетах имеют два последние потенциала - энергия Гельмгольца F и энергия Гиббса G, т.к. их естественные переменные наиболее удобны для измерения и фиксирования в ходе химических превращений. Функции F и G имеют дополнительный физико-химический смысл. Изменение энергии Гельмгольца в каком-либо процессе при Т = const, V = const равно максимальной работе, которую может совершить система при обратимом процессе: 1 2
Термодинамические потенциалы Таким образом, энергия F равна той части внутренней энергии ( U = F + TS), которая может превратиться в работу. Аналогично, изменение энергии Гиббса в каком-либо процессе при Т = const, р = const равно максимальной полезной (т.е. немеханической) работе, которую может совершить система в этом процессе: 1 3
Расчет изменения энергии Гиббса и энергии Гельмгольца в различных процессах 1 4
Изменение энергий Гиббса и Гельмгольца при изменении температуры Зависимость энергии Гиббса и Гельмгольца от температуры в закрытых системах может быть определена с помощью фундаментальных уравнений: dF = -SdT - pdV, dG = -SdT + Vdp или с помощью уравнения Гиббса – Гельмгольца: 1 5
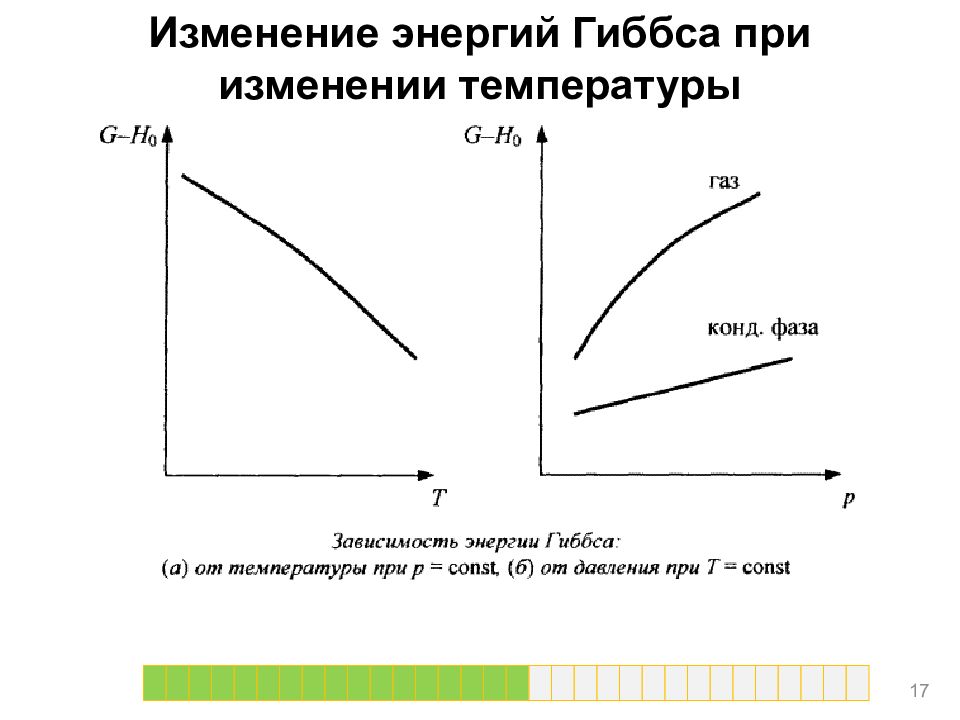
Изменение энергий Гиббса и Гельмгольца при изменении температуры Функции F и G являются функциями состояния, для них: Для интегрирования этих уравнений надо знать температурную зависимость энтропии, которая определяется теплоемкостью системы. Зависимость энергии Гиббса от температуры в предположении линейной температурной зависимости теплоемкости приведена на рисунке. 1 6
Изменение энергий Гиббса при изменении температуры 1 7
Изменение энергий Гиббса при изотермическом расширении (сжатии) Зависимость энергии Гиббса и Гельмгольца от давления и объема при постоянной температуре может быть определена интегрированием соответствующих производных. 1 8
Изменение энергий Гиббса при изотермическом расширении (сжатии) Для восстановления вида этой зависимости необходимо знать уравнение состояния фазы. Так, для идеального газа: Если р1 = р о = 1 бар, то говорят о стандартной энергии Гиббса, G о 1 9
Изменение энергий Гиббса при химической реакции Расчет изменения функции G в химических реакциях можно проводить разными способами. Рассмотрим три из них. 20
Изменение энергий Гиббса при химической реакции 1. По определению, G = Н - TS. Если продукты реакции и исходные вещества находятся при одинаковой температуре, то изменение энергии Гиббса в химической реакции 21
Изменение энергий Гиббса при химической реакции 2. Аналогично тепловому эффекту реакции, изменение энергии Гиббса можно рассчитать, используя стандартные энергии Гиббса образования реагентов и продуктов Изменение энергии Гельмгольца химической реакции между идеальными газами связано с энергией Гиббса Δ v - изменение количества молей газообразных веществ в ходе реакции. Для реакций в конденсированной фазе при небольших давлениях: 22
Изменение энергий Гиббса при химической реакции 3. Стандартная энергия Гиббса реакции может быть рассчитана с помощью стандартных приведенных потенциалов, где G о (Т) - стандартное значение энергии Гиббса при температуре Т, Н о (0), Н о (298) - стандартные значения энтальпии при температурах 0 и 298 К. 23
Изменение энергий Гиббса при химической реакции Функции Ф о (Т) и Ф' о (Т) (приведенная энергия Гиббса) вычисляются для газов по молекулярным данным, а для конденсированных фаз - на основании экспериментальных данных по теплоемкости. Связь между приведенными потенциалами и стандартной энергией Гиббса реакции выражается соотношениями: 24
Расчет изменения энергии Гиббса при смешении Изменение энтропия при смешении равняется: На основании равенства энтропии и частной производной энергии Гиббса по температуре, взятой с отрицательным знаком, самостоятельно выводим выражение. 25
Методы приближенного расчета энергии Гиббса 1. Метод Улиха. При отсутствии данных зависимости теплоемкости от температуры Δ Ср=а, где а – выбирается на основании приблизительной оценки теплоемкостей при комнатной температуре. При этом получается следующая зависимость: 26
Методы приближенного расчета энергии Гиббса 2. Метод Темкина-Шварцмана. Если изменение теплоемкости задано полиномом: то где 27
Методы приближенного расчета энергии Гиббса 2. Метод Темкина-Шварцмана (продолжение). Если изменение теплоемкости задано полиномом: то 28
Методы приближенного расчета энергии Гиббса 29 2. Метод Темкина-Шварцмана (окончание).
Использование ПО для термодинамического моделирования системы 30
31
32
