Национальный исследовательский Томский политехнический университет «Прикладная химическая термодинамика» Смороков Андрей Аркадьевич wolfraum@yandex.ru vk.com/wolfraum1993 1
Опрос 2
1. Что происходит с реальным газом при температуре Бойля, согласно вириальному уравнению? 2. Приведите основные методы измерения изобарной теплоемкости. 3. Одним из уравнений, хорошо описывающих зависимость изобарной теплоемкости вещества от температуры, является уравнение Йококава, имеет следующий вид: Ср= a + b ∙ T + c ∙ T -2 + d ∙ T 2 + e ∙ T -3. Приведите расчетное уравнение Кирхгофа для вещества, изобарная теплоемкость которого описывается уравнением Йококава, в диапазоне температур от 298 К до 500 К при а=а 0, b = b 0, c = c 0, d = d 0 и e = e 0. 4. Дайте определение стандартной энтальпии реакции. 3
Законы термодинамики Первый закон термодинамики определяет энергетический баланс различных процессов, в том числе химических реакций. Второй закон позволяет предсказать, при каких условиях процесс возможен и каким будет его результат при заданных условиях. Создание вечных двигателей 1 и 2 рода идут в противопоставление с 1 и 2 законом термодинамики соответственно. 4
Вечные двигатели Вечный двигатель первого рода – неограниченно долго действующее устройство, способное бесконечно совершать работу без затрат топлива или других энергетических ресурсов. Вечный двигатель второго рода – неограниченно долго действующая машина, которая, будучи пущена в ход, превращала бы в работу всё тепло, извлекаемое из окружающих тел. 5
Второй закон термодинамики Существует экстенсивная функция состояния термодинамической системы – энтропия (S). При протекании в изолированной системе обратимых процессов эта функция остается неизменной, а при необратимых – увеличивается. Знак равенства относится к обратимым процессам, а знак больше - к необратимым. Энтропия изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума. 6
Источники необратимых процессов Источником необратимого процесса может быть диффузия, расширение системы при существовании разности давлений между ней и окружающей средой, теплопередача при разных температурах, самопроизвольные химические реакции в объеме системы и другие диссипативные процессы, связанные с необратимым превращением работы в теплоту. 7
Объединенный 1 и 2 законы термодинамики (Фундаментальное уравнение Гиббса) Для нахождения взаимосвязи между энтропией и другими термодинамическими величинами необходимо связать 1 и 2 начало термодинамики. dS и dU – характеристические функции. Функции под знаком дифференциала ( U, V и т.д.) – естественные переменные. Функция является характеристической, если, используя ее и ее частные производные, можно выразить любое термодинамическое свойство системы. 8
Взаимосвязь термодинамических параметров системы между собой Из фундаментального уравнения Гиббса следует, что частные производные энтропии по экстенсивным переменным U, V и n i могут быть выражены через интенсивные свойства системы 9
Условия равновесия При изолированной системе А + В и двух открытых друг другу системах А и В имеем: и поскольку U, V и n – постоянные, то получаем: 10
Условие равновесия Если в качестве внешних переменных для каждой из подсистем «А» и «В» выбрать их объем и количества веществ, то полный дифференциал функции S = S ( U, V, n ) для каждой из подсистем запишется в виде: А производные: 11
Условие равновесия Исходя из выше описанного и получаем: 12
Условие равновесия Согласно второму закону термодинамики, при равновесии энтропия изолированной системы достигает максимума, то есть dS(U,V,n) = 0. Изменения dU(A), dV(A) dn i (A) не связаны между собой, поэтому равенство нулю dS(U,V,n) может быть только в том случае, если равен нулю каждый из коэффициентов, стоящих в квадратных скобках, то есть: 13
Условие равновесия Записывая крайние частные производные в явном виде, получаем условия равновесия между двумя открытыми подсистемами: Если хотя бы некоторые из этих условий не выполняются, то система является неравновесной, и в ней могут происходить релаксационные процессы, сопровождающиеся выравниванием соответствующих термодинамических сил. 14
Соотношения Максвелла Исходя из фундаментального уравнения Гиббса возможно выделить некоторые полезные соотношения между частными производными, называемыми соотношениями Максвелла. Критерием равенства соотношений является равенство вторых смешанных производных функции состояния. 15
Соотношения Максвелла (пример) Рассмотрим изменение внутренней энергии по энтропии и объему. Т.к. dU - полный дифференциал, частные производные внутренней энергии по естественным переменным равны. При дифференцировании первого тождества по объему, а второго - по энтропии, то получатся перекрестные вторые частные производные внутренней энергии, которые равны друг другу 16
Мнемоническое правило соотношений Максвелла T (теперь ), V( всё ), S( стало ), P( понятно) Т (теперь) V (всё) S (стало) p (понятно) Если есть пересечение стрел, то «ставим крест» на минусе (минусов нет). Например: 17
Мнемоническое правило соотношений Максвелла T (теперь ), V( всё ), S( стало ), P( понятно) Т (теперь) V (всё) S (стало) p (понятно) Если нет пересечения, то ставим минус. Например: 18
Мнемоническое правило соотношений Максвелла T (теперь ), V( всё ), S( стало ), P( понятно) Т (теперь) V (всё) S (стало) p (понятно) 19
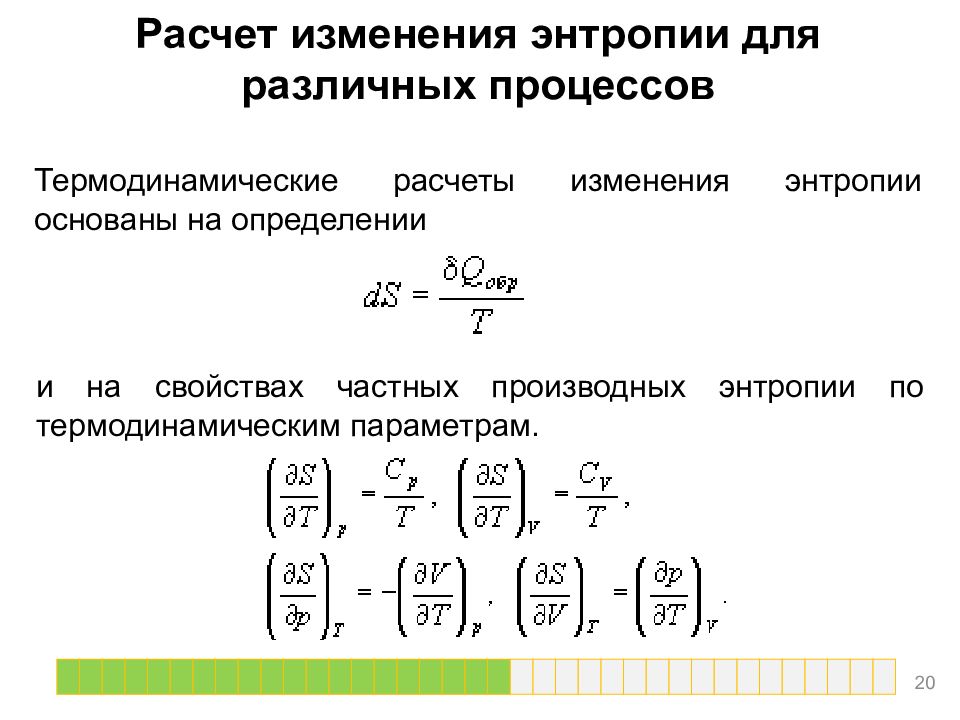
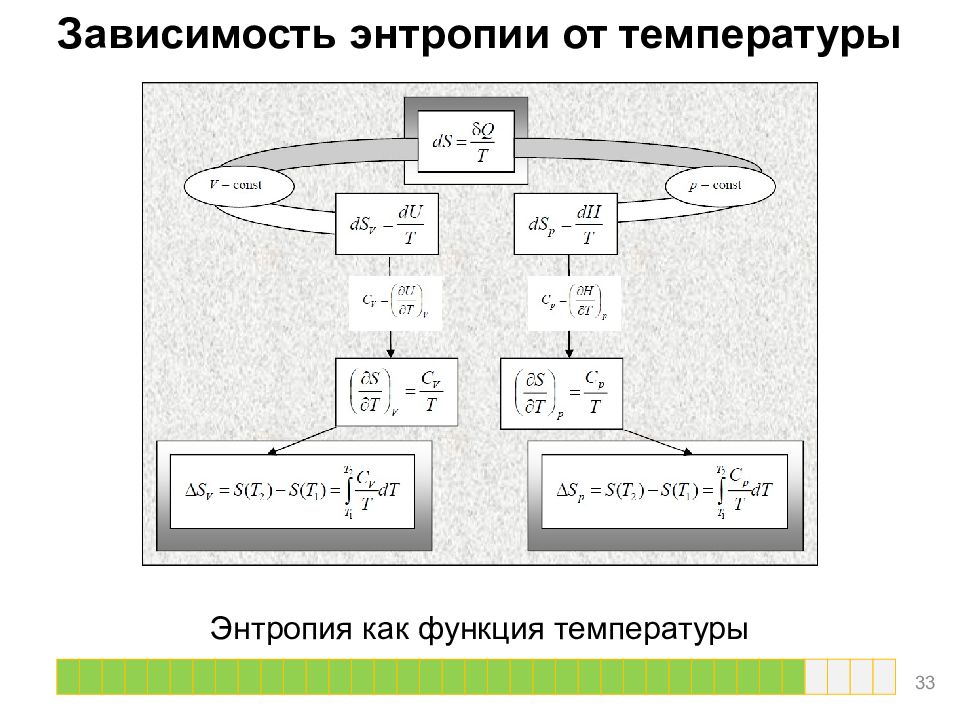
Расчет изменения энтропии для различных процессов Термодинамические расчеты изменения энтропии основаны на определении и на свойствах частных производных энтропии по термодинамическим параметрам. 20
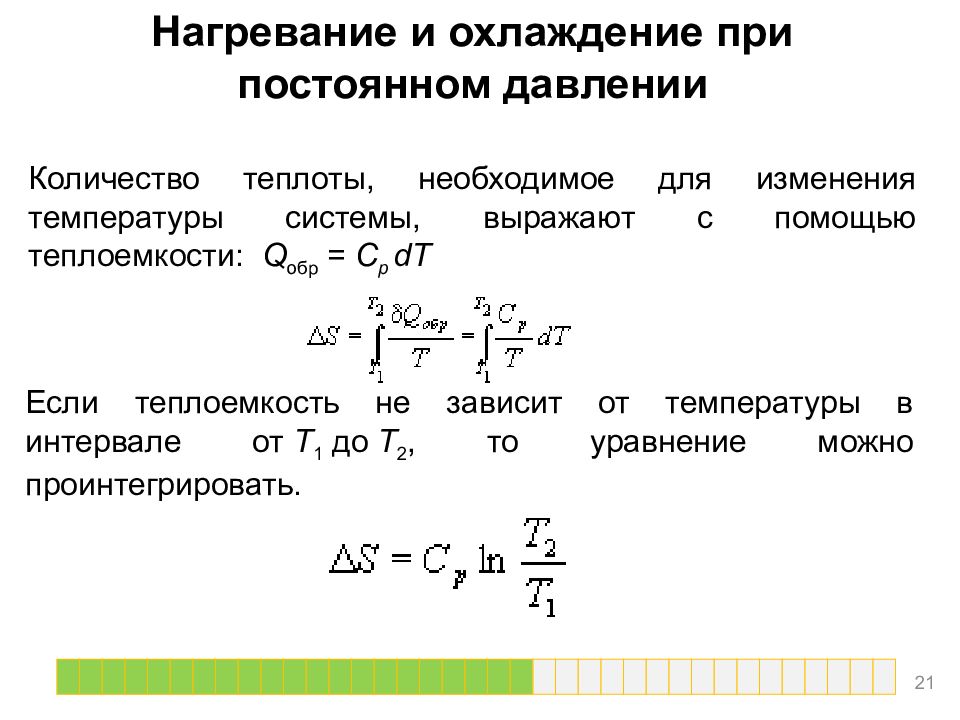
Нагревание и охлаждение при постоянном давлении Количество теплоты, необходимое для изменения температуры системы, выражают с помощью теплоемкости: Q обр = C p dT Если теплоемкость не зависит от температуры в интервале от T 1 до T 2, то уравнение можно проинтегрировать. 21
Нагревание и охлаждение при постоянном давлении В случае описания теплоемкости рядом вида: Cp = a + bT + c/T То, после интегрирования, соответствующее изменение энтропии равняется Если изменение температуры происходит при постоянном объеме, то в формулах C p надо заменить на C V. 22
Изотермическое расширение или сжатие Для расчета энтропии в этом случае надо знать уравнение состояния системы. Расчет основан на использовании соотношения Максвелла. В частности, для изотермического расширения идеального газа ( p = nRT / V ) 23
Фазовые переходы При обратимом фазовом переходе температура остается постоянной, а теплота фазового перехода при постоянном давлении равна H фп, поэтому изменение энтропии равно: При плавлении и кипении теплота поглощается, поэтому энтропия в этих процессах возрастает: S тв < S ж < S г. При этом энтропия окружающей среды уменьшается на величину Δ S ф.п., поэтому изменение энтропии Вселенной равно 0, как и полагается для обратимого процесса в изолированной системе. 24
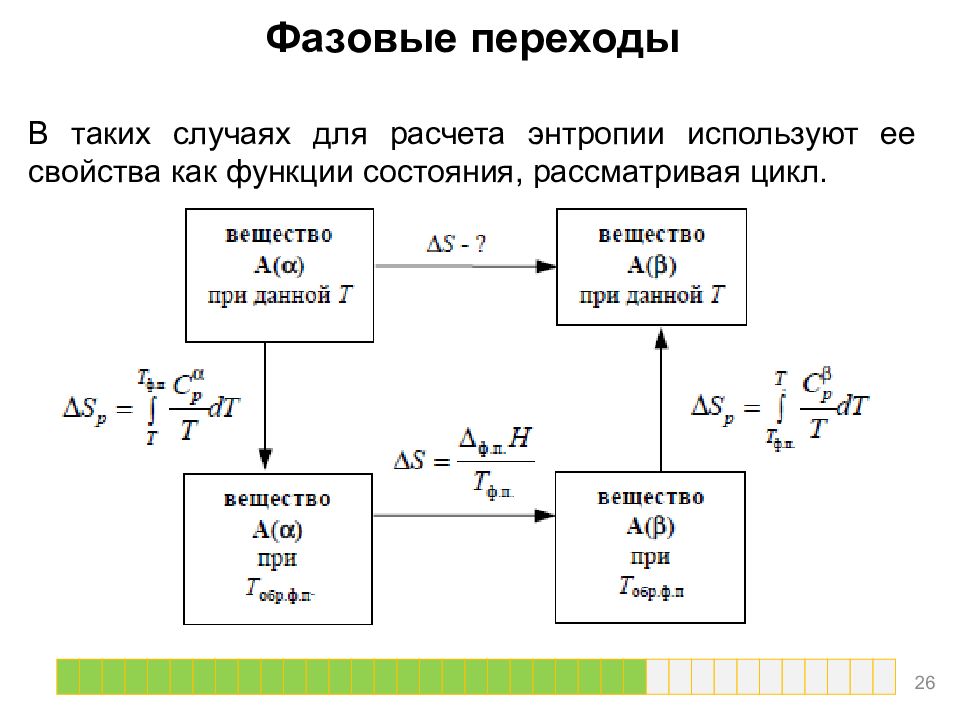
Фазовые переходы Если фазовый переход происходит при температуре, отличной от температуры обратимого фазового перехода, то использовать формулу нельзя, так как согласно второму началу термодинамики при необратимых процессах В таких случаях для расчета энтропии используют ее свойства как функции состояния, рассматривая цикл 25
Фазовые переходы В таких случаях для расчета энтропии используют ее свойства как функции состояния, рассматривая цикл. 26
Фазовые переходы (пример) Рассчитать изменение энтропии 1000 г воды в результате ее замерзания при –5 °С. Теплота плавления льда при 0 °С равна 6008 Дж/моль. Теплоемкости льда и воды равны 34.7 и 75.3 Дж/(К⋅моль), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс – самопроизвольный. 27
Фазовые переходы (решение) Решение. Необратимый процесс кристаллизации воды при темпера туре –5 °С можно представить в виде последовательности обратимых процессов: 1) нагревание воды от –5 °С до температуры кристаллизации (0 °С); 2) кристаллизация воды при 0 °С; 3) охлаждение льда от 0 до –5 °С: Так как энтропия – функция состояния, общее изменение энтропии равно сумме по этим трем процессам: Изменение энтропии в 1 и 3 процессах (при изменении температуры) рассчитывается по формуле: Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода. Необходимо только иметь в виду, что теплота при кристаллизации выделяется: Энтропия при кристаллизации убывает, хотя процесс самопроизвольный. Это связано с тем, что в окружающую среду выделяется теплота и энтропия окружающей среды увеличивается, причем это увеличение больше, чем 1181 Дж/К, поэтому энтропия Вселенной при кристаллизации воды возрастает, как и полагается в необратимом процессе. Ответ: -1181 Дж/К. 28
Смешение идеальных газов при постоянной температуре и давлении Если n 1 молей одного газа, занимающего объем V 1, смешиваются с n 2 молями другого газа, занимающего объем V 2, то общий объем будет равен V 1 + V 2, причем газы расширяются независимо друг от друга и общее изменение энтропии равно сумме изменений энтропии каждого газа: где x i - мольная доля i -го газа в полученной газовой смеси. Изменение энтропии всегда положительно, т.к. все ln x i < 0, поэтому идеальные газы всегда смешиваются необратимо. Если при тех же условиях смешиваются две порции одного и того же газа, то уравнение уже неприменимо. При этом Δ S = 0. Это противоречие называют парадоксом Гиббса. 29
Изменение энтропии при химических реакциях Разность мольных энтропий продуктов реакции и реагентов, взятых в стандартных состояниях, называется стандартной энтропией реакции. Для реакции стандартная энтропия реакции равна разности абсолютных энтропий продуктов и реагентов с учетом стехиометрических коэффициентов 30
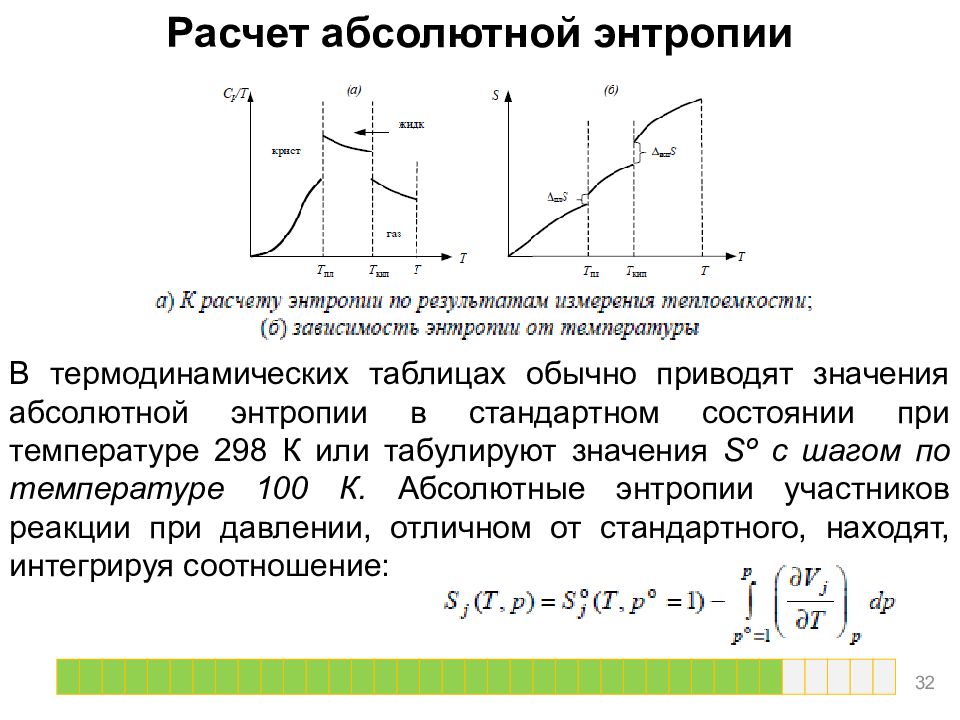
Расчет абсолютной энтропии Для расчета абсолютной энтропии веществ в стандартном состоянии надо знать зависимости теплоемкости Cp от температуры для каж дой из фаз, а также температуры и энтальпии фазовых переходов. Так, например, абсолютная энтропия газообразного вещества в стандартном состоянии при температуре T складывается из следующих составляю щих стандартная энтропия реакции равна разности абсолютных энтропий продуктов и реагентов с учетом стехиометрических коэффициентов 31
Расчет абсолютной энтропии В термодинамических таблицах обычно приводят значения абсолютной энтропии в стандартном состоянии при температуре 298 К или табулируют значения Sº с шагом по температуре 100 К. Абсолютные энтропии участников реакции при давлении, отличном от стандартного, находят, интегрируя соотношение: 32
Зависимость энтропии от температуры Энтропия как функция температуры 33
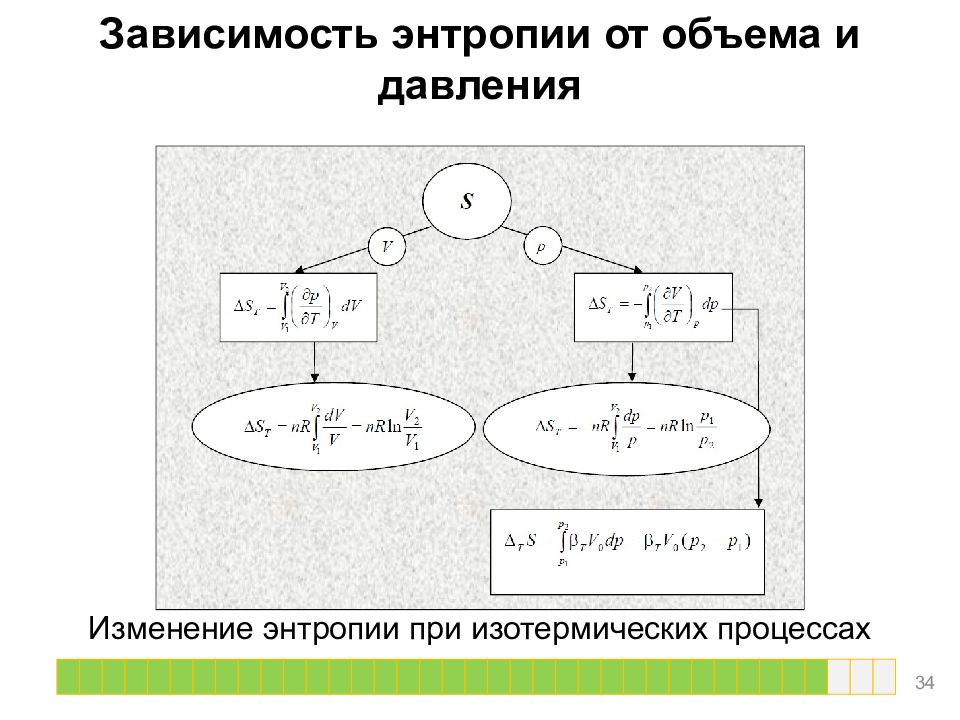
Зависимость энтропии от объема и давления Изменение энтропии при изотермических процессах 34
Третий закон термодинамики Абсолютное значение энтропии, полученное при интегрировании для обратимых процессов, известно с точностью до постоянной интегрирования ( S 0 ) Значение этой постоянной устанавливается третьим законом термодинамики - при нулевой абсолютной температуре энтропия любых веществ, находящихся в равновесном состоянии, имеет одно и то же значение, не зависящее от фазового состояния вещества. В изотермических процессах, происходящих при T = 0, энтропия не зависит ни от обобщенных сил, ни от обобщенных координат. 35
Третий закон термодинамики Так как при 0 К энтропия всех веществ одинакова, то конкретное значение S 0 несущественно и его можно принять равным нулю (постулат Планка), т.е. при абсолютном нуле все идеальные кристаллы имеют одинаковую энтропию, равную нулю. Используя понятие абсолютной энтропии, следует помнить, что вывод о постоянстве S 0 относится лишь к полностью равновесным при 0 К системам. На самом деле при понижении температуры уменьшаются скорости релаксационных процессов, и в веществе может «замораживаться» некоторая остаточная энтропия 36
Третий закон термодинамики Статистическое определение энтропии основано на идее о том, что необратимые процессы в термоди намике вызваны переходом системы в более вероятное состояние, поэтому энтропию можно связать с вероятностью: S=klnW k – постоянная Больцмана ( k = R/N A ), W – так называемая термоди намическая вероятность, т.е. число микросостояний, которые соответствуют данному макросостоянию системы 37
