Надежность информационных систем Курс лекций Автор: д. т. н., профессор Малыш В. Н. Липецк 2011
Надежность информационных систем Основные понятия и теоремы теории вероятностей
Надёжность изделия зависит от многочисленного комплекса факторов, определяемых как внутренними свойствами изделия, так и воздействием внешних условий. Это приводит к тому, что процесс возникновения отказов, а также другие характеристики надёжности носят случайный характер. Для исследования случайных явлений используются вероятностные методы. Рассмотрим понятие событие. Событие - это всякий факт, который в результате опыта может произойти или не произойти.
Примеры событий: А - появление герба при бросании монеты. В - попадание в цель при выстреле. С - отказ изделия. Д - безотказная работа изделия. Событие достоверное - если оно обязательно появляется в результате данного опыта. Невозможное событие - если оно не может появиться в результате данного опыта. Случайное событие - событие, которое может появиться, а может и не появиться в результате данного опыта.
Вероятность события - это степень возможности появления этого события. Более вероятными являются те события, которые происходят чаще. Менее вероятными являются те события, которые происходят реже. Мало вероятными являются те события, которые почти никогда не происходят. Достоверному событию можно приписать вероятность, равную единице. Невозможному событию можно приписать вероятность, равную нулю. P(A) - вероятность события А.
Рассмотрим последовательность n одинаковых опытов. Предположим, что в результате каждого опыта регистрируется появление или непоявление некоторого события А. Пусть: m - число появлений события А при n опытах; n - общее число произведённых опытов. P * ; здесь P * (A) - частота события А. При n → ∞, P*(A) → P (A).
Частота события P*(A) при n → ∞ сходится по вероятности к вероятности этого события P ( A ). где Е - любое наперёд заданное, сколь угодно малое положительное число.
Классификация событий Несколько событий в данном опыте образуют полную группу событий, если в результате опыта должно появиться хотя бы одно из них. Примеры событий, образующих полную группу: 1) выпадение герба и выпадение цифры при бросании монеты; 2) появление 1,2,3,4,5,6 очков при бросании игральной кости; 3) попадание и промах при выстреле; 4) безотказная работа изделия и отказ изделия.
Несовместные события : несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе. Если в данном опыте могут иметь место два несовместных события, то они называются противоположными. А - событие (безотказная работа изделия); A - противоположное событие (отказ изделия). Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий A =A 1 +A 2 +…+A n.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий A =A 1 A 2 …A n. Если в данном опыте могут иметь место два несовместных события, то они называются противоположными. Теорема сложения вероятностей Вероятность суммы n несовместных событий равна сумме вероятностей этих событий P(A 1 +A 2 +…+A n )= P(A 1 )+P(A 2 )+…+P(A n )
Сумма вероятностей n несовместных событий, образующих полную группу событий, равна единице: P(A 1 )+P(A 2 )+…+P(A n )=1; где A 1,A 2,…,A n - несовместные события, образующие полную группу. Следствие: сумма вероятностей двух противоположных событий равна единице: P(A)+P( A )=1.
Теорема умножения вероятностей Зависимое событие - это такое событие, вероятность которого зависит от того, произошли или не произошли остальные события. Независимое событие - это такое событие, вероятность которого не зависит от того, произошли или не произошли остальные события. Вероятность произведения n независимых событий равна произведению вероятностей этих событий P(A 1 A 2 …A n )= P(A 1 )P(A 2 )…P(A n ).
Теорема умножения вероятностей Условная вероятность P(A/B): P(A/B) - условная вероятность события А при условии, что событие В имело место. Вероятность произведения двух событий равна произведению вероятности 1-го события на условную вероятность 2-го события, при условии, что 1-ое событие имело место: P(A 1 A 2 )= P(A 1 )P(A 2 /A 1 ).
Теорема полной вероятности Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий H 1,H 2,…H n. События H 1,H 2,…H n образуют полную группу n несовместных событий. Будем называть эти события гипотезами. Вероятность события А определяется формулой полной вероятности : где P(H i ) - вероятность осуществления гипотезы H i ; P(A/H i ) - условная вероятность события А при условии, что событие H i имело место.
Количественные характеристики надёжности Случайная величина - величина, которая в результате опыта может принять то или иное значение, причём заранее неизвестно, какое именно. Примеры случайной величины: 1) интервал времени между соседними отказами ЭВМ; 2) интервал времени от начала работы изделия до первого отказа или время безотказной работы; 3) число деталей, изготовленных рабочим в единицу времени. Обозначим через T - время безотказной работы изделия (интервал времени от начала работы изделия до первого отказа). T – случайная величина. Величина T также называется наработка на отказ изделия. t - возможные значения случайной величины T. Введём понятие “вероятность безотказной работы”.
Вероятность безотказной работы: вероятность того, что в пределах заданной наработки отказ объекта не возникает. На практике этот показатель определяется статистической оценкой. где N 0 - число однотипных объектов (элементов), поставленных на испытания (находящихся под контролем); во время испытаний отказавший объект не восстанавливается и не заменяется исправным; n(t) - число отказавших объектов за время t. Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени, причем она является убывающей функцией и может принимать значения от 1 до 0.
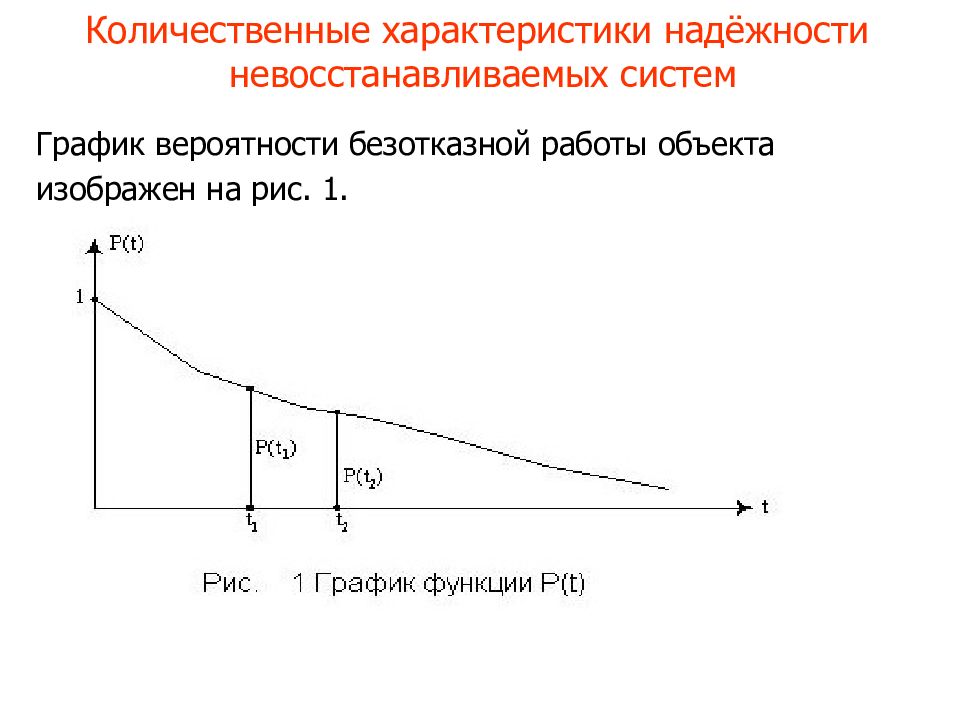
График вероятности безотказной работы объекта изображен на рис. 1.
Как видно из графика, функция P(t) характеризует изменение надежности во времени и является достаточно наглядной оценкой. Например, на испытания поставлено 1000 образцов однотипных элементов, то есть No = 1000 изоляторов. При испытании отказавшие элементы не заменялись исправными. За время t отказало 10 изоляторов. Следовательно, P(t) = 0,99 и наша уверенность состоит в том, что любой изолятор из данной выборки не откажет за время t с вероятностью P(t) = 0,99. Иногда практически целесообразно пользоваться не вероятностью безотказной работы, а вероятностью отказа Ф(t).
Вероятность безотказной работы имеет следующие достоинства: характеризует надежность во времени, являясь интервальной оценкой; определяет многие важные показатели техники: эффективность, безопасность, живучесть, риск; сравнительно просто вычисляется и определяется по статистическим данным об отказах техники; достаточно полно характеризует надежность невосстанавливаемой техники. Основной недостаток этого критерия - ограниченность применения, т.к. он характеризует надежность невосстанавливаемой техники или восстанавливаемой до первого ее отказа.
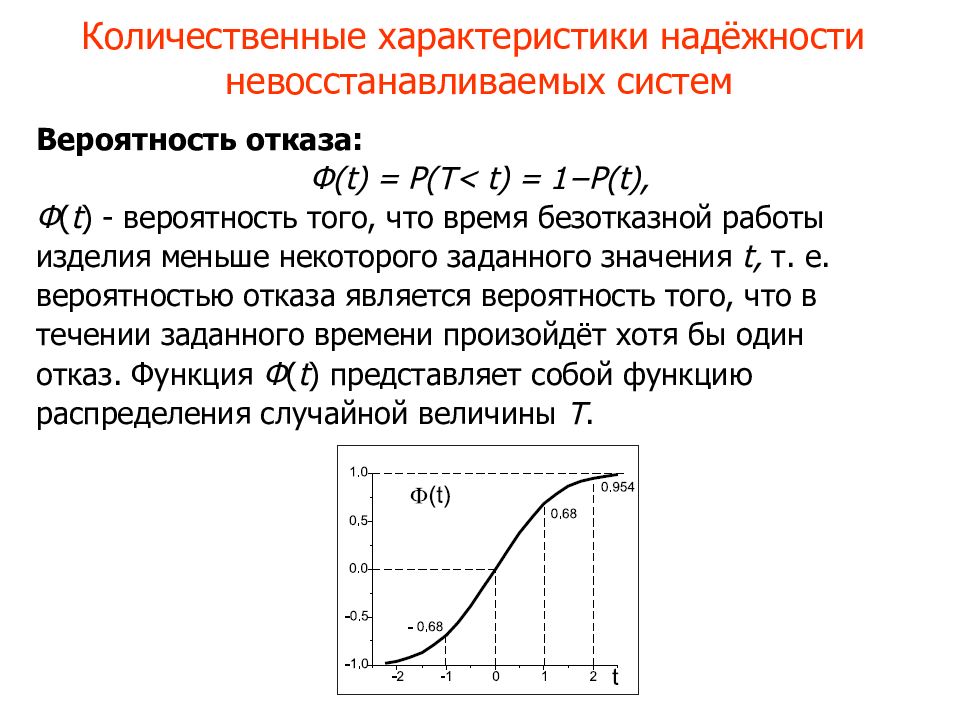
Вероятность отказа: Ф(t) = P(T< t) = 1−P(t), Ф ( t ) - вероятность того, что время безотказной работы изделия меньше некоторого заданного значения t, т. е. вероятностью отказа является вероятность того, что в течении заданного времени произойдёт хотя бы один отказ. Функция Ф ( t ) представляет собой функцию распределения случайной величины Т.
Поскольку работоспособность и отказ являются состояниями несовместными и противоположными, то их вероятности связаны зависимостью: Р(t) + Ф(t) = 1, следовательно: Ф(t) = 1 - Р(t). Статистическая оценка вероятности отказа:
Производная от вероятности отказа по времени есть плотность вероятности или дифференциальный закон распределения времени работы объекта до отказа где F(t) – функция распределения времени до отказа ; f * (t) – плотность распределения времени безотказной работы (частота отказов). Наиболее полно характеризует надежность техники в данный момент (точечная характеристика). По ней можно определить любой показатель надежности невосстанавливаемой системы. Это основное достоинство распределения времени безотказной работы. d Ф( t ) dt
Статистически f * (t) определяется отношением числа отказавших образцов техники в единицу времени к числу испытуемых образцов при условии, что отказавшие образцы не восполняются исправными. где n(t,t+ Δ t) – число отказавших образцов за промежуток времени (t,t+ Δ t), N 0 – число образцов, первоначально поставленных на испытания.
Интенсивность отказов Определяется отношением плотности распределения к вероятности безотказной работы объекта: λ (t) = Статистически интенсивность отказов есть отношение отказавших образцов техники в единицу времени к среднему числу образцов, исправно работающих на интервале (t,t+ Δ t) :
где среднее число исправно работающих образцов на интервале (t,t+ Δ t). На основании определения интенсивности отказов: или Интегрируя последнее выражение, получим:
Или Интенсивность отказов λ (t) является основным показателем надежности элементов сложных систем. Это можно объяснить следующими обстоятельствами: надежность многих элементов можно оценить одним числом, т.к. интенсивность отказа элементов – величина постоянная; λ (t) обладает хорошей наглядностью ; интенсивность отказов нетрудно получить экспериментально.
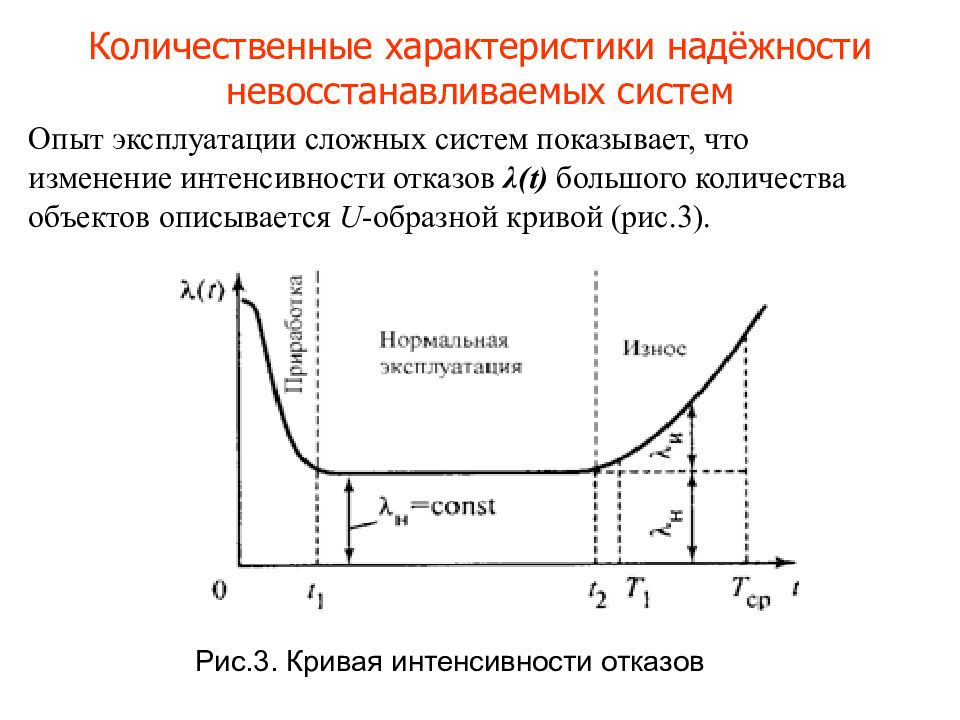
Опыт эксплуатации сложных систем показывает, что изменение интенсивности отказов λ (t) большого количества объектов описывается U - образной кривой (рис.3). Рис.3. Кривая интенсивности отказов
Время функционирования объекта можно разделить на три характерных участка: период приработки (0, t 1 ) ; период нормальной эксплуатации ( t 1, t 2 ) ; период износа (старения) объекта ( t>t 2 ). Период приработки объекта имеет повышенную интенсивность отказов, вызванную приработочными отказами, обусловленными дефектами производства, монтажа и наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем. В период нормальной эксплуатации интенсивность отказов практически остается постоянной, при этом отказы носят случайный характер.
При этом отказы носят случайный характер и появляются внезапно, прежде всего из-за случайных изменений нагрузки, несоблюдения условий эксплуатации, неблагоприятных внешних факторов и т.п. Именно этот период соответствует основному времени эксплуатации объекта. Возрастание интенсивности отказов относится к периоду старения объекта и вызвано увеличением числа отказов из-за износа, старения и других причин, связанных с длительной эксплуатацией.
Среднее время безотказной работы Средним временем безотказной работы Т 1 называется математическое ожидание времени безотказной работы объекта: Т 1 = М ( ξ ). По статистическим данным об отказах Т 1 определяется следующей зависимостью: где N 0 – число испытуемых образцов техники, t i – время безотказной работы i - го образца.
Среднее время безотказной работы Как математическое ожидание случайной величины плотностью f(t), среднее время безотказной работы вычисляется по формуле: Интегрируя по частям, получим:
Среднее время безотказной работы Первое слагаемое равно нулю, т.к. P(0)=1, P( +∞ )= 0, и тогда выражение для Т 1 будет иметь вид: Среднее время безотказной работы является интегральным показателем надежности. Его основное достоинство – высокая наглядность. Недостаток этого показателя в том, что он, будучи интегральным, характеризует надежность техники длительного времени работы.
Показателями надежности восстанавливаемых элементов и систем могут быть также показатели надежности невосстанавливаемых элементов. Это имеет место в тех случаях, когда система, в состав которой входит элемент, является неремонтируемой по условиям ее работы (необитаемый космический аппарат, аппаратура, работающая в агрессивных средах, самолет в процессе полета и т.п.). Надежность восстанавливаемых объектов оценивается следующими показателями: Т – среднее время работы между отказами (средняя наработка на отказ); Т в – среднее время восстановления; w(t) – параметр потока отказов;
К г ( t ) – функция готовности – вероятность того, что система исправна в момент t ; К п ( t ) – функция простоя – вероятность того, что в момент t система неисправна и восстанавливается; К г – коэ ффициент готовности – вероятность того, что система будет исправной при длительной эксплуатации (стационарный режим); К п – коэ ффициент простоя – вероятность того, что система будет неисправной при длительной эксплуатации.
Среднее время работы между отказами и среднее время восстановления Среднее время между отказами Т определяется отношением средней суммарной наработки к среднему числу отказов при длительной работе объекта. Среднее время восстановления Т в определяется отношением среднего суммарного времени восстановления к среднему числу восстановлений при длительной работе. По статистическим данным среднее время между отказами Т определяется по формуле:
где t i - время между отказами i – го образца, полученное при условии, что испытания ведутся с восстановлением отказавших образцов техники или их заменой. В этом случае число испытуемых образцов N 0 остается постоянным. Параметр потока отказов Параметром потока отказов w(t) называется производная (скорость изменения) среднего числа отказов объекта в момент t. Статистически параметр потока отказов определяется как отношение числа отказавших образцов техники в единицу времени к числу образцов, поставленных на испытание при условии, испытания ведутся с восстановлением отказавших образцов техники или их заменой:
где n(t,t+ Δ t) – число отказавших образцов за промежуток времени (t,t+ Δ t), N 0 – число образцов, первоначально поставленных на испытания. Параметр потока отказов обладает следующими свойствами: в случае экспоненциального закона времени работы объекта с параметром λ и мгновенного восстановления w(t) = λ ; при мгновенном восстановлении предел, к которому стремится параметр потока отказов при t →∞, равен величине, обратной среднему времени безотказной работы, т.е.
при мгновенном восстановлении параметр потока отказов и плотность распределения времени до отказа связаны следующим интегральным уравнением Вольтерра второго рода: Это уравнение устанавливает зависимость между показателями надежности восстанавливаемой и невосстанавливаемой техники. Оно позволяет определить по статистическим данным об отказах восстанавливаемой техники в процессе ее эксплуатации показатели надежности невосстанавливаемой техники.
Функция готовности и функция простоя Функцией готовности К г ( t ) называется вероятность того, что восстанавливаемая система исправна в момент времени t. Функцией простоя К п ( t ) называется вероятность того, что в момент времени t система находится в отказовом состоянии (в ремонте). Основные соотношения между введенными показателями: К г ( t ) + К п ( t ) = 1.
Коэффициент готовности и коэффициент простоя
