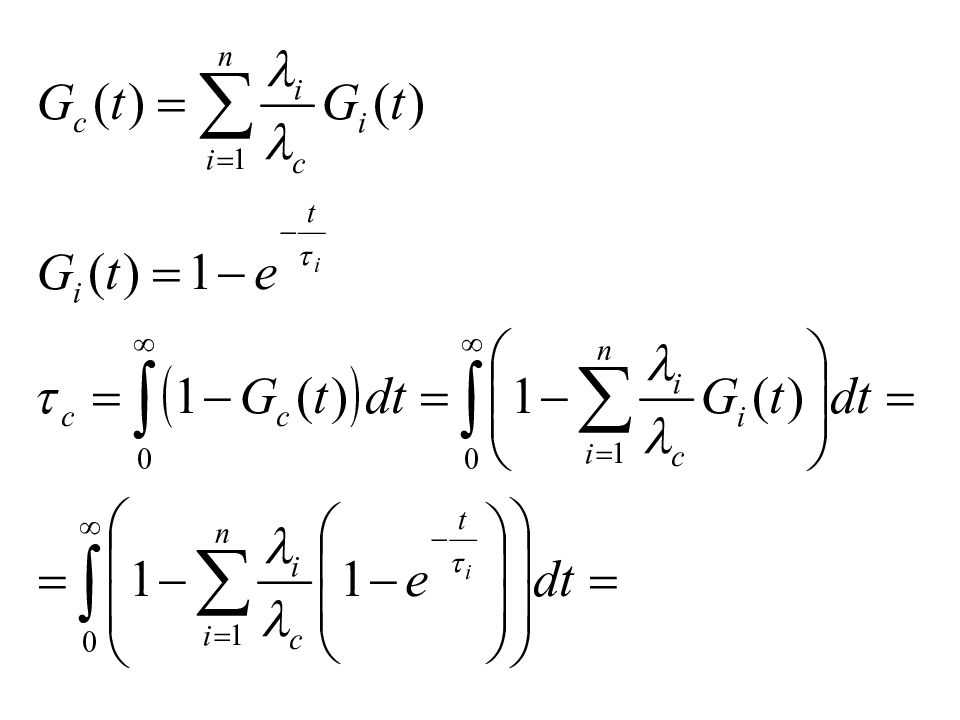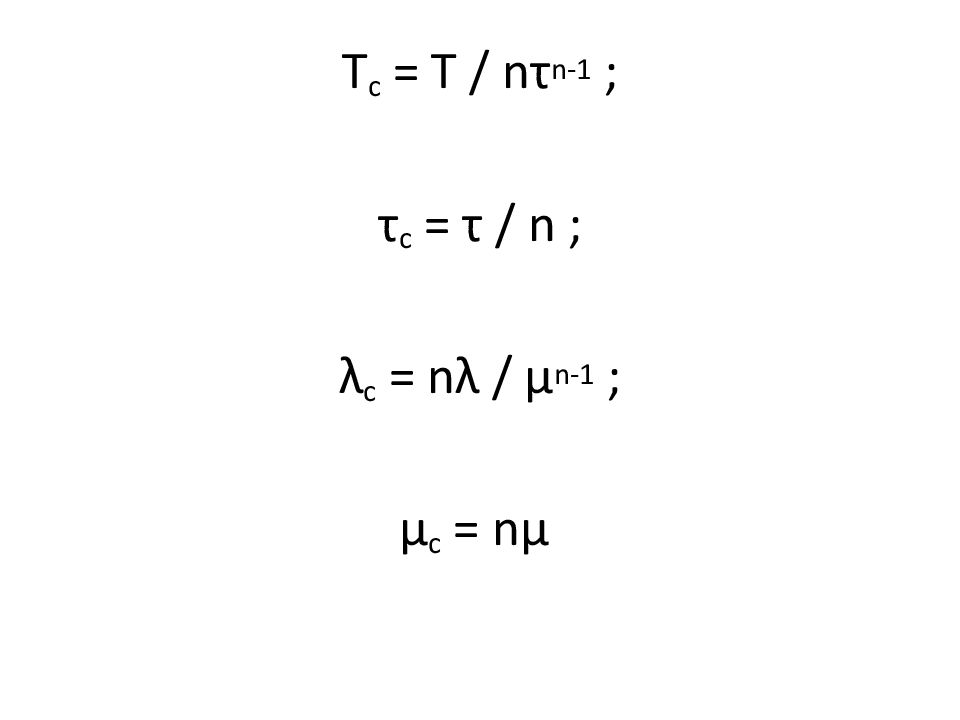Первый слайд презентации: Теория надежности в электроэнергетике
Преподаватель – к.т.н., доцент, Лапидус Александр Анатольевич Lapidus_a_a@mail.ru ; 534-48-00; 8-921-358-84-16 кафедра «Электрические станции и автоматизация энергетических систем»
1.1. Определение надежности 1.2. Свойства, характеризующие надежность 1.3. Состояния, характеризующие надежность объектов энергетики 1.4. События, характеризующие надежность объектов энергетики 1.5. Средства обеспечения надежности объектов энергетики
2.1. Множества 2.2. События 2.3. Вероятность 2.4. Элементы комбинаторики 2.4.1. Перестановки 2.4.2. Размещения 2.4.3. Сочетания 2.5. Случайные величины и их распределения 2.5.1. Числовые характеристики распределений 2.5.2. Законы распределения дискретных случайных величин 2.5.3. Законы распределения непрерывных случайных величин
Слайд 5: Глава 3. Показатели надежности
3.1. Невосстанавливаемые объекты 3.2. Объекты с мгновенным восстановлением 3.3. Объекты с конечным временем восстановления 3.4. Показатели надежности электрических сетей и систем электроснабжения
Слайд 6: Глава 4. Вероятностные модели для расчета надежности
4.1. Общие положения 4.2. Последовательное соединение элементов 4.3. Параллельное соединение элементов 4.4. Последовательно-параллельное соединение элементов 4.5. Метод минимальных путей и сечений 4.6. Метод декомпозиции
Слайд 7: Литература
1. Гук Ю. Б., Карпов В. В., Лапидус А. А. Теория надежности. Введение: учеб. пособие. – СПб. : Изд-во Политехн. ун-та, 2010. – 165 с. 2. Гук Ю. Б., Карпов В. В. Расчеты надежности электрических сетей и систем: Учеб. пособие. – Л. : Изд. ЛПИ, 1990. 3. Гук Ю. Б., Синенко М. М., Тремясов В. А. Расчет надежности схем электроснабжения. – Л. : Энергоатомиздат, 1990. 4. ГОСТ 27.002-89. Надежность в технике. Основные понятия. Термины и определения : введ. 01.07.90. – М., 1989.
Слайд 8: Глава 1. Определение основных понятий
1.1. Определение надежности Задумаемся, что такое НАДЕЖНОСТЬ
Слайд 9
ГОСТ 27.002-89 Надежность в технике. Основные понятия. Термины и определения «Надежность – это свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения, транспортировки.»
Слайд 10
В энергетике: Надежность – это свойство объекта выполнять заданные функции в заданном объеме. Заданные функции – бесперебойное и безопасное снабжение потребителя электроэнергией требуемого качества
Слайд 11: 1.2. Свойства, характеризующие надежность
Вообще выделяют следующие свойства: В электроэнергетике к ним можно добавить: 1. Безотказность 2. Долговечность 3. Ремонтопригодность 4. Сохраняемость 5. Устойчивоспособность 6. Режимная управляемость 7. Живучесть 8. Безопасность
Слайд 12: Свойства, характеризующие надежность
1. Безотказность – свойство объекта непрерывно сохранять работоспособное состояние ( РСС ) в течение некоторого времени или некоторой наработки. РСС – когда значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют нормативам. Наработка – объем работы объекта (ч, м3, кВтч и т.д.)
Слайд 13: Свойства, характеризующие надежность
2. Долговечность – свойство объекта сохранять РСС до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Предельное состояние – когда дальнейшее применение объекта по назначению недопустимо или нецелесообразно, либо восстановление невозможно или невыгодно.
Слайд 14: Свойства, характеризующие надежность
3. Ремонтопригодность – свойство объекта быть приспособленным к предупреждению и обнаружению причин отказов, к поддержанию и восстановлению работоспособности путем технического обслуживания, ремонта, замены. Отказ – переход объекта на более низкий уровень работоспособности. Отказы – полные и частичные.
Слайд 15: Свойства, характеризующие надежность
4. Сохраняемость – свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение и после хранения, транспортировки.
Слайд 16: Свойства, характеризующие надежность в электроэнергетике
5. Устойчивоспособность – свойство объекта непрерывно сохранять устойчивость в течение заданного времени.
Слайд 17: Свойства, характеризующие надежность в электроэнергетике
6. Режимная управляемость – свойство объекта поддерживать нормальный режим посредством управления.
Слайд 18: Свойства, характеризующие надежность в электроэнергетике
7. Живучесть – свойство объекта противостоять возмущениям, не допуская их каскадного развития с массовым нарушением питания потребителей.
Слайд 19: Свойства, характеризующие надежность в электроэнергетике
8. Безопасность – свойство объекта не допускать ситуации, опасные для людей и окружающей среды. Безопасность – настолько важное свойство, что его часто выделяют из понятия надежности.
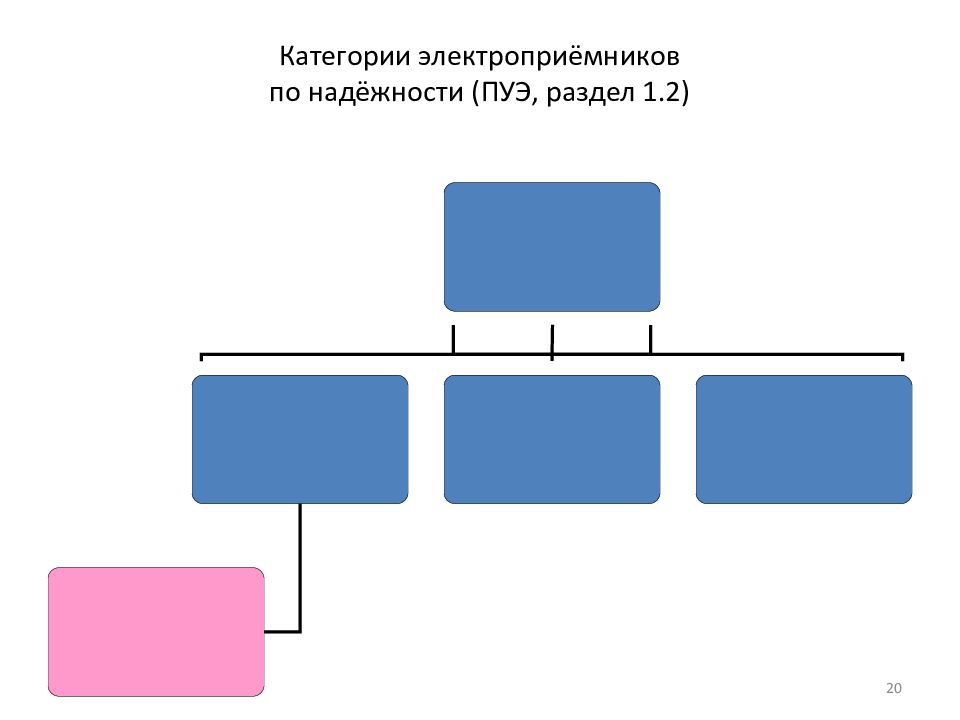
Слайд 20: Категории электроприёмников по надёжности (ПУЭ, раздел 1.2)
20 Категории электроприёмников по надёжности (ПУЭ, раздел 1.2)
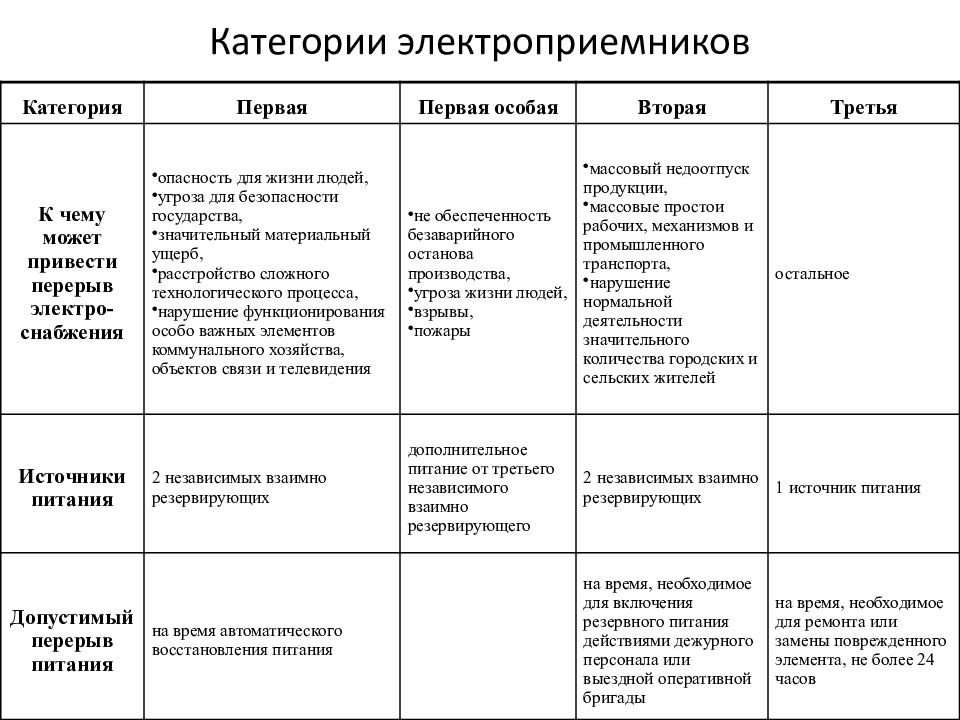
Слайд 21: Категории электроприемников
21 Категории электроприемников Категория Первая Первая особая Вторая Третья К чему может привести перерыв электро-снабжения опасность для жизни людей, угроза для безопасности государства, значительный материальный ущерб, расстройство сложного технологического процесса, нарушение функционирования особо важных элементов коммунального хозяйства, объектов связи и телевидения не обеспеченность безаварийного останова производства, угроза жизни людей, взрывы, пожары массовый недоотпуск продукции, массовые простои рабочих, механизмов и промышленного транспорта, нарушение нормальной деятельности значительного количества городских и сельских жителей остальное Источники питания 2 независимых взаимно резервирующих дополнительное питание от третьего независимого взаимно резервирующего 2 независимых взаимно резервирующих 1 источник питания Допустимый перерыв питания на время автоматического восстановления питания на время, необходимое для включения резервного питания действиями дежурного персонала или выездной оперативной бригады на время, необходимое для ремонта или замены поврежденного элемента, не более 24 часов
Слайд 22: 1.3. Состояния, характеризующие надежность
Работоспособное – когда объект способен выполнять заданные функции; Неработоспособное ; Рабочее – когда объект выполняет заданные функции; Нерабочее ; Предельное – см. п. 1.2; Резервное – рабочее состояние объекта, при котором он осуществляет резервирование других объектов; Зависимый простой – нерабочее состояние работоспособного объекта, возникающее вследствие отключения других объектов или проведения на них работ, требующих отключения данного объекта.
Слайд 23: 1.4. События, характеризующие надежность объектов энергетики
1) Отказ работоспособности 2) Отказ функционирования 3) Авария 4) Восстановление
Слайд 24: 1.4. События, характеризующие надежность объектов энергетики
1) Отказ работоспособности – переход объекта на более низкий уровень работоспособности; 2) Отказ функционирования – переход объекта на более низкий уровень функционирования; Для объектов, функционирующих не непрерывно отказы функционирования делятся на:
Слайд 25: 2) Отказы функционирования:
Отказ срабатывания – отказ функционирования, заключающийся в невыполнении объектом требуемого срабатывания ; Ложное срабатывание – отказ функционирования, заключающийся в срабатывании объекта при отсутствии требования срабатывания Излишнее срабатывание – отказ функционирования, заключающийся в срабатывании объекта при требовании срабатывания других объектов и отсутствии требования срабатывания данного объекта
Слайд 26: События, характеризующие надежность объектов энергетики
3) Авария – переход объекта на существенно более низкий уровень работоспособности (или функционирования) с серьёзным нарушением режима работы объекта. 4) Восстановление – повышение уровня работоспособности (или функционирования), которое осуществляется в результате: а) аварийного, планового, внепланового ремонта; б) профилактического обслуживания.
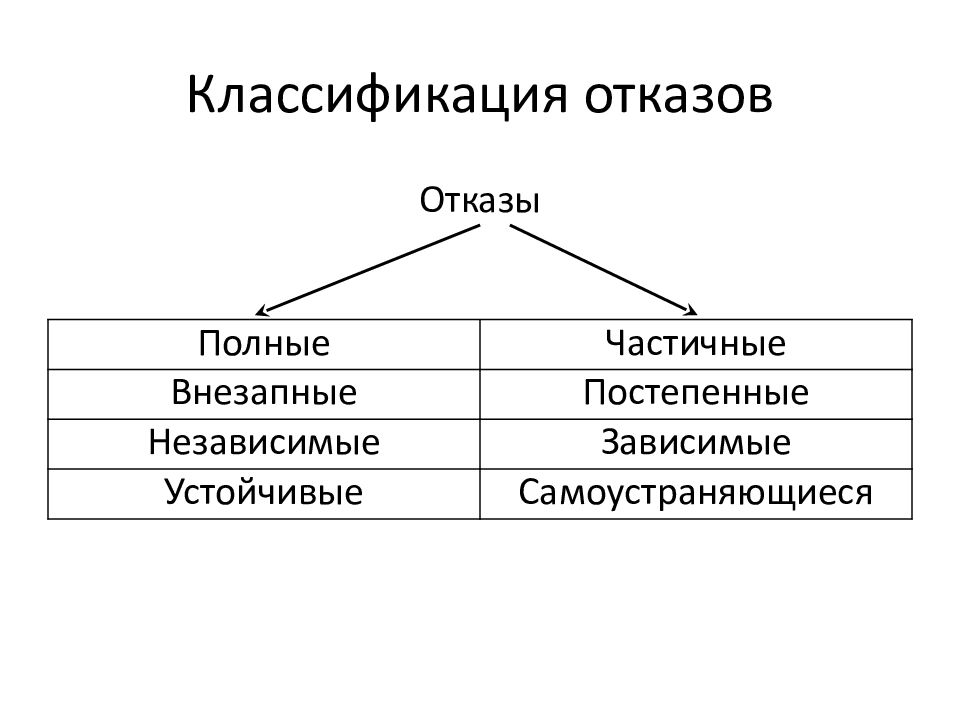
Слайд 27: Классификация отказов
Полные Частичные Внезапные Постепенные Независимые Зависимые Устойчивые Самоустраняющиеся Отказы
Слайд 28: 1.5. Средства обеспечения надежности объектов энергетики
Резервирование – повышение надежности объекта введением избыточности; Техническое обслуживание – работы для поддержания исправности или работоспособности объекта при подготовке к использованию по назначению; Ремонт – работы для поддержания или восстановления исправности или работоспособности объекта; Техническая диагностика – контроль за уровнем работоспособности; Диспетчерское управление (ручное и автоматическое) – управление режимом энергосистемы и входящих в неё энергетических объектов, осуществляемое в процессе производства, преобразования и распределения электроэнергии; Релейная защита и автоматика.
Слайд 29: Виды резервирования
Структурное Функциональное Временн ό е Информационное Постоянное (неявное) Замещением (явное)
Слайд 30: Виды резервирования
Структурное – использование избыточных элементов структуры. Функциональное – использование способности элементов выполнять дополнительные функции. Временн ό е – использование избыточного времени, когда системе предоставляется дополнительное время для решения задачи.
Слайд 31: Виды резервирования
Информационное – использование избыточной информации. Постоянное (неявное) – когда резервный элемент предварительно нагружен, а при отказе резервируемого элемента система продолжает выполнять требуемые функции без переключений. Замещением (явное) – когда функции резервируемого элемента передаются резервному только после отказа резервируемого элемента.
Слайд 32: Виды резервов
Ремонтный – для восполнения вывода в плановый ремонт; Оперативный – для компенсации небаланса между генерируемой и потребляемой мощностями; Аварийный – для восполнения аварийного выхода из строя; Нагрузочный – для восприятия случайных колебаний нагрузки; Эксплуатационный (= номинальная мощность минус текущая)
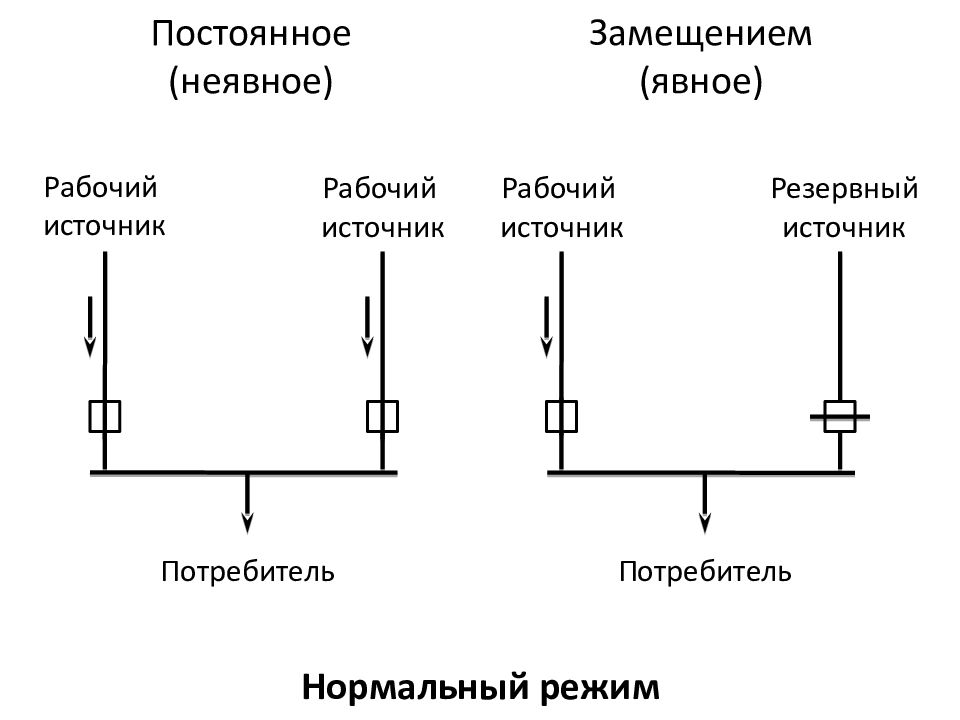
Слайд 33
Постоянное (неявное) Рабочий источник Рабочий источник Рабочий источник Резервный источник Потребитель Потребитель Замещением (явное) Нормальный режим
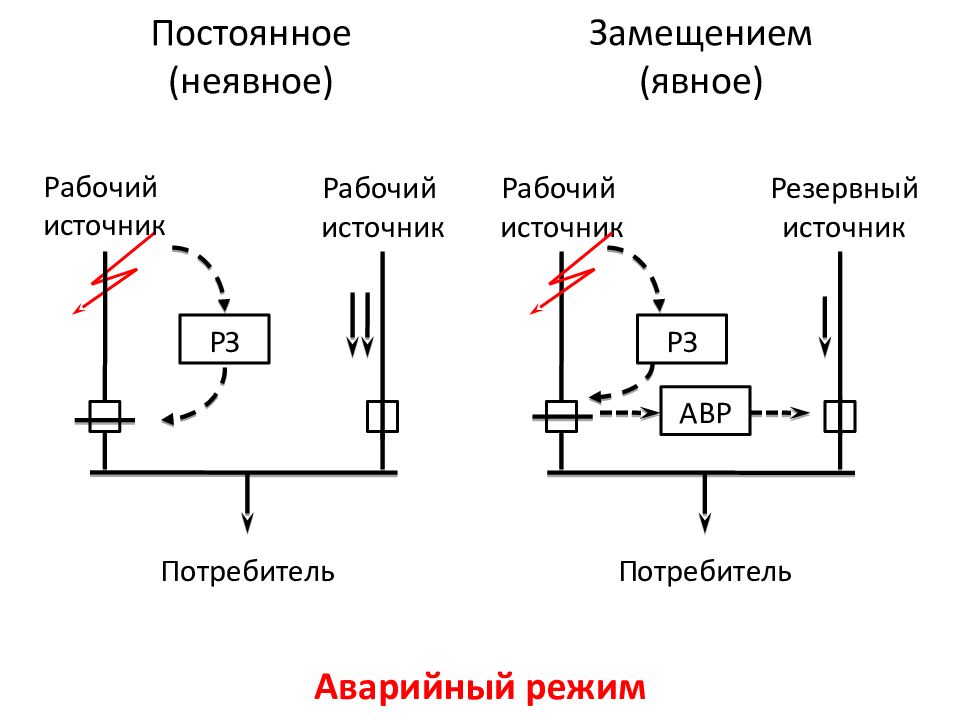
Слайд 34
Постоянное (неявное) Замещением (явное) Аварийный режим Рабочий источник Рабочий источник Рабочий источник Резервный источник Потребитель Потребитель РЗ АВР РЗ
Слайд 35: Баланс мощности в день максимума нагрузки в 2013 году (18 января, пятница, 10.00): Руст = 223,1 ГВт; Ограничения: 14,7 ГВт; Авар. и внеплан. рем.: 2,8 ГВт; Плановые ремонты: 19,7 ГВт; Резерв: 38,1 ГВт; Экспорт: 2,2 ГВт; Потребление: 147,1 ГВт (66%)
Примечание: Невыпускаемый резерв обусловлен ограничениями пропускной способности сетей в ОЭС Северо-Запада, Сибири и Востока
Слайд 36: Анализ видов, последствий и критичности отказов
ГОСТ 27.310-95. Надежность в технике. Анализ видов, последствий и критичности отказов. Основные положения. связывает: тяжесть последствий отказов; ожидаемую частоту возникновения отказа; требуемую глубину анализа отказа.
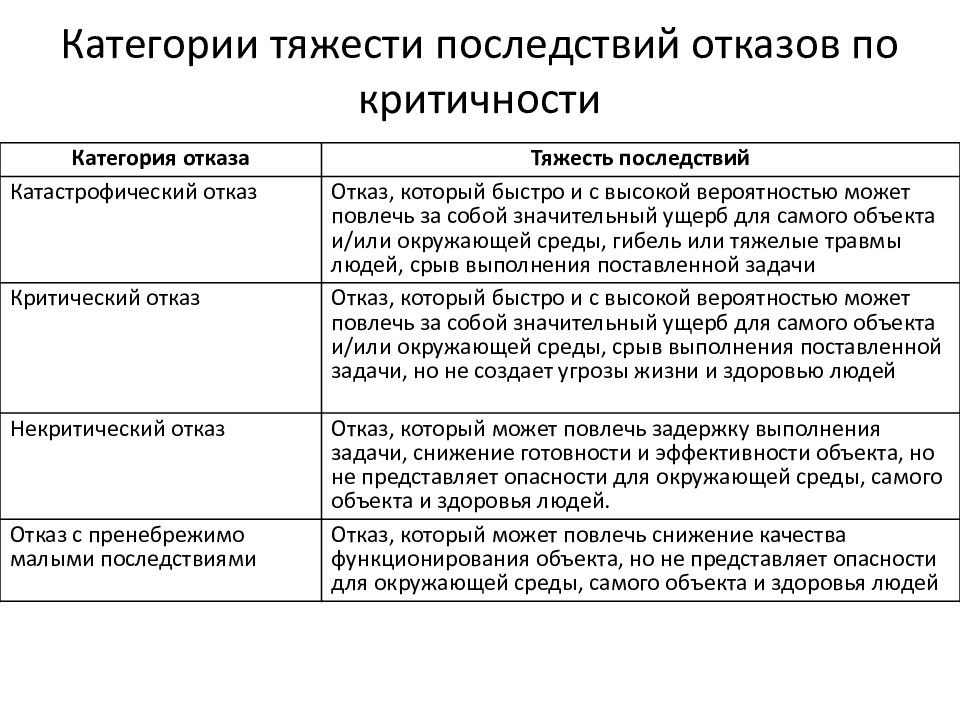
Слайд 37: Категории тяжести последствий отказов по критичности
Категория отказа Тяжесть последствий Катастрофический отказ Отказ, который быстро и с высокой вероятностью может повлечь за собой значительный ущерб для самого объекта и/или окружающей среды, гибель или тяжелые травмы людей, срыв выполнения поставленной задачи Критический отказ Отказ, который быстро и с высокой вероятностью может повлечь за собой значительный ущерб для самого объекта и/или окружающей среды, срыв выполнения поставленной задачи, но не создает угрозы жизни и здоровью людей Некритический отказ Отказ, который может повлечь задержку выполнения задачи, снижение готовности и эффективности объекта, но не представляет опасности для окружающей среды, самого объекта и здоровья людей. Отказ с пренебрежимо малыми последствиями Отказ, который может повлечь снижение качества функционирования объекта, но не представляет опасности для окружающей среды, самого объекта и здоровья людей
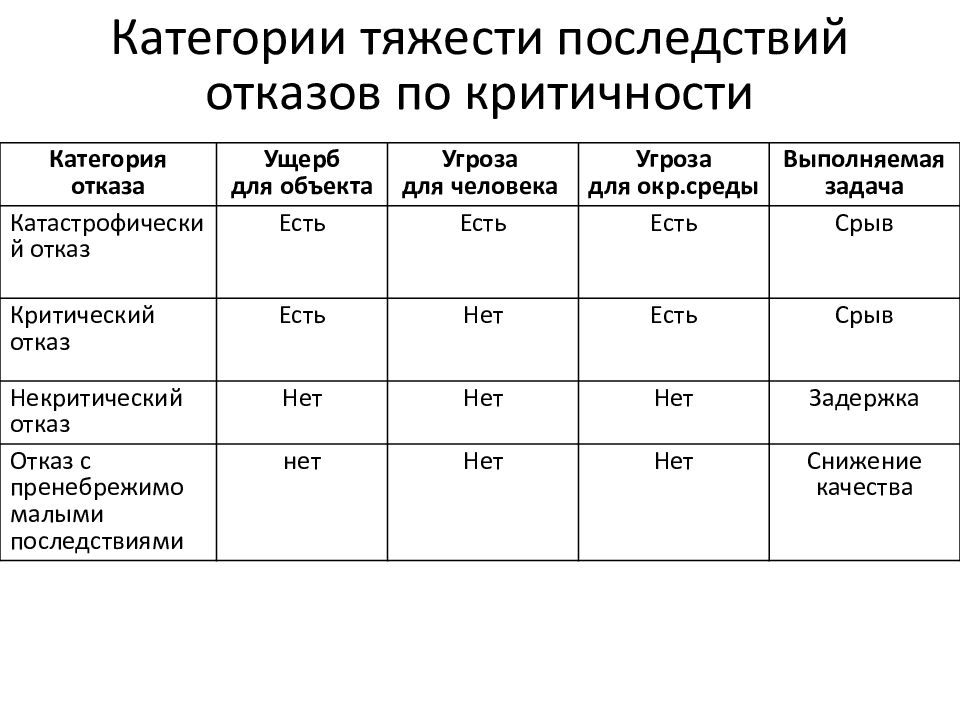
Слайд 38: Категории тяжести последствий отказов по критичности
Категория отказа Ущерб для объекта Угроза для человека Угроза для окр.среды Выполняемая задача Катастрофический отказ Есть Есть Есть Срыв Критический отказ Есть Нет Есть Срыв Некритический отказ Нет Нет Нет Задержка Отказ с пренебрежимо малыми последствиями нет Нет Нет Снижение качества
Слайд 39: Ранги отказов по требуемой глубине анализа
А обязателен углубленный количественный анализ В желателен количественный анализ С можно ограничиться качественным анализом D анализ не требуется
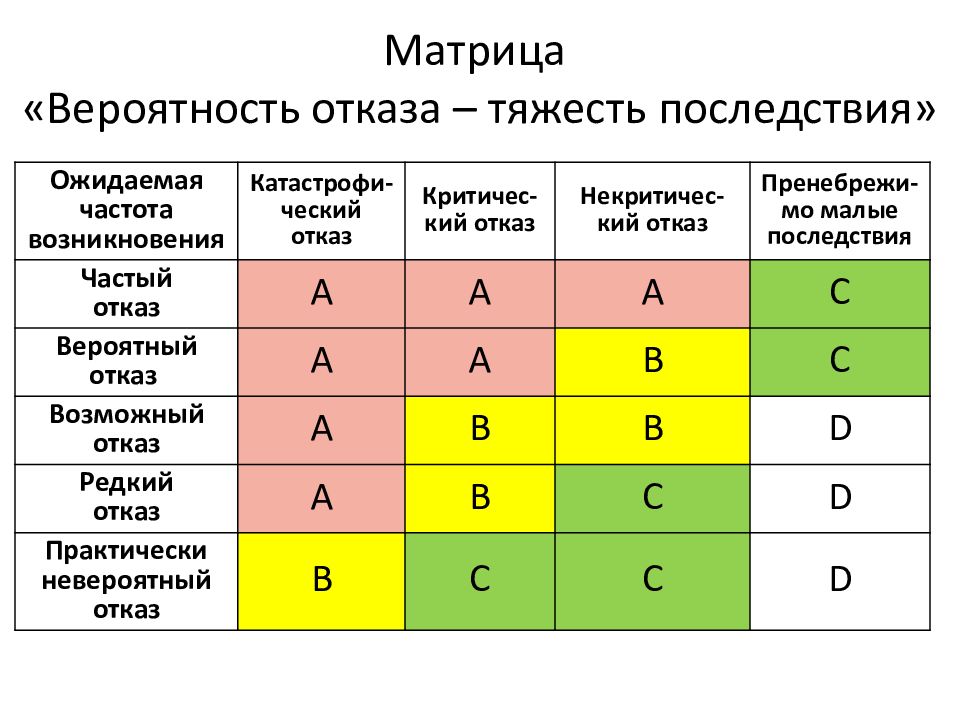
Слайд 40: Матрица «Вероятность отказа – тяжесть последствия»
Ожидаемая частота возникновения Катастрофи-ческий отказ Критичес-кий отказ Некритичес-кий отказ Пренебрежи-мо малые последствия Частый отказ А А А С Вероятный отказ А А В С Возможный отказ А В В D Редкий отказ А В С D Практически невероятный отказ В С С D
Слайд 41: Глава 2. Элементы теории вероятности
2.1. Множества Множество – совокупность элементов А = { a 1 ; a 2 ; … ; a n } Если n = 0, то это пустое множество. Если n = ∞, то это бесконечное множество.
Слайд 42: Соотношения между множествами
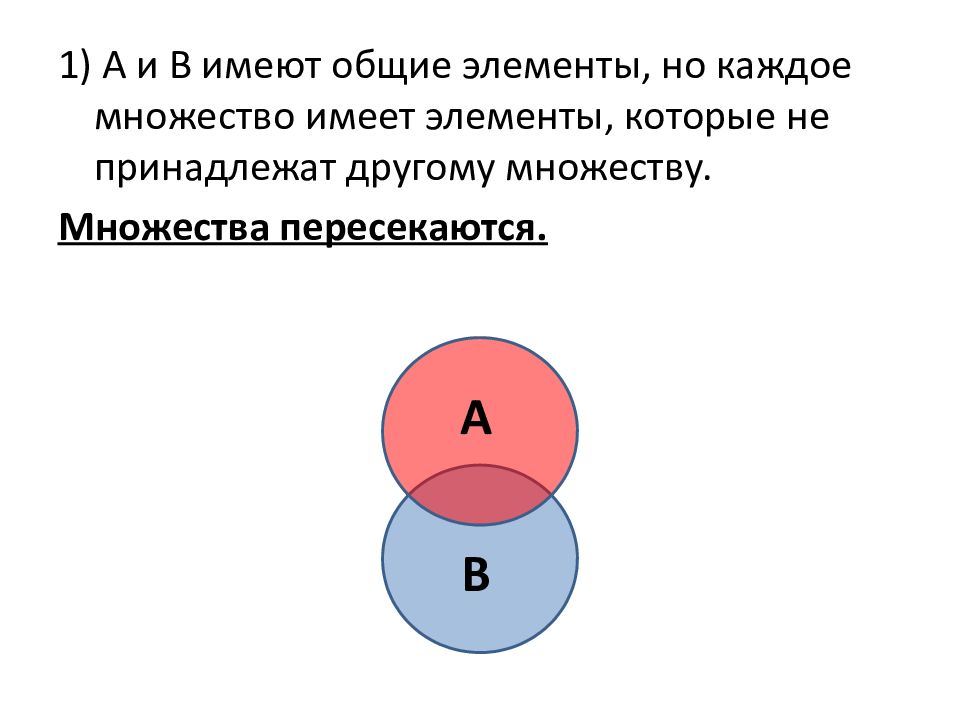
Соотношения между множествами определяются наличием или отсутствием общих элементов. Диаграммы Эйлера-Венна:
Слайд 43
1) А и В имеют общие элементы, но каждое множество имеет элементы, которые не принадлежат другому множеству. Множества пересекаются. А В
Слайд 45
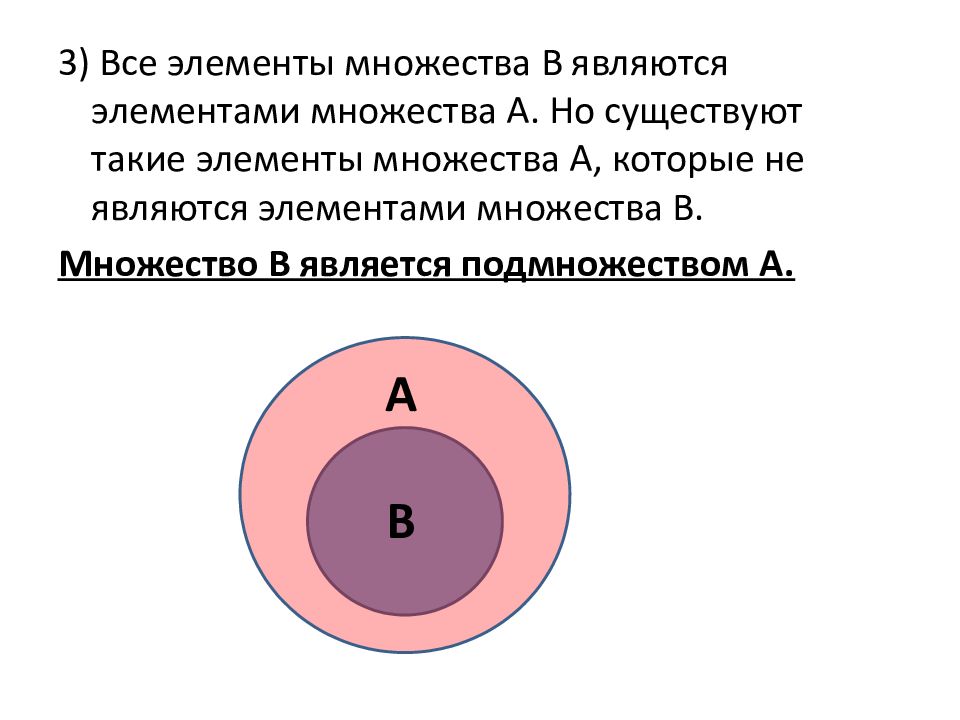
3) Все элементы множества В являются элементами множества А. Но существуют такие элементы множества А, которые не являются элементами множества В. Множество В является подмножеством А. А В
Слайд 46
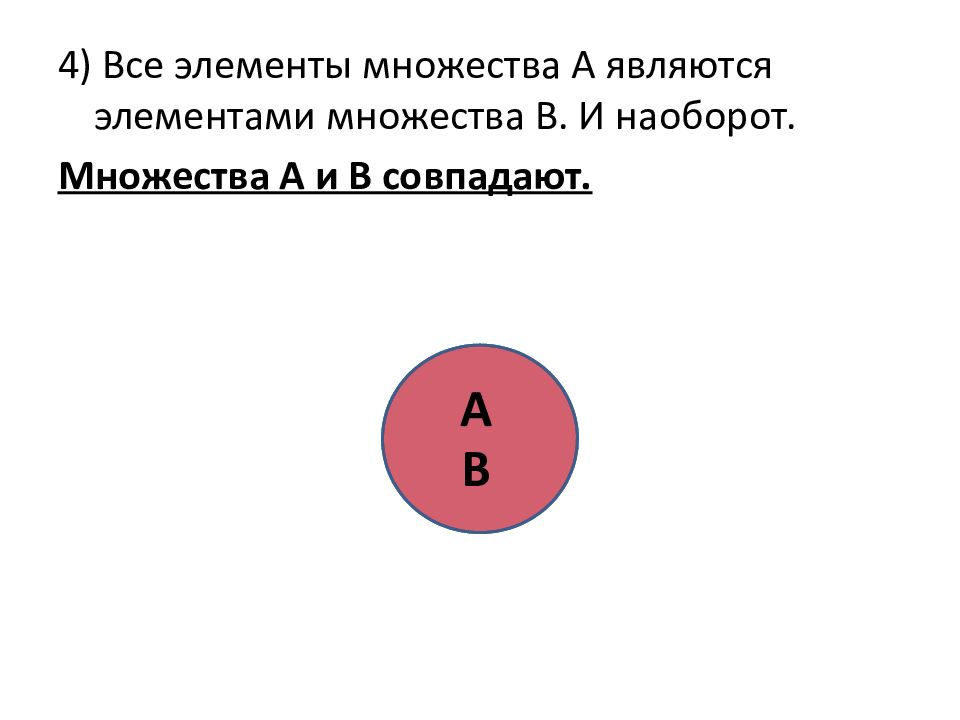
4) Все элементы множества А являются элементами множества В. И наоборот. Множества А и В совпадают. А В
Слайд 47: Операции над множествами
а) Объединение б) Пересечение в) Разность г) Дополнение
Слайд 48: а) Объединение
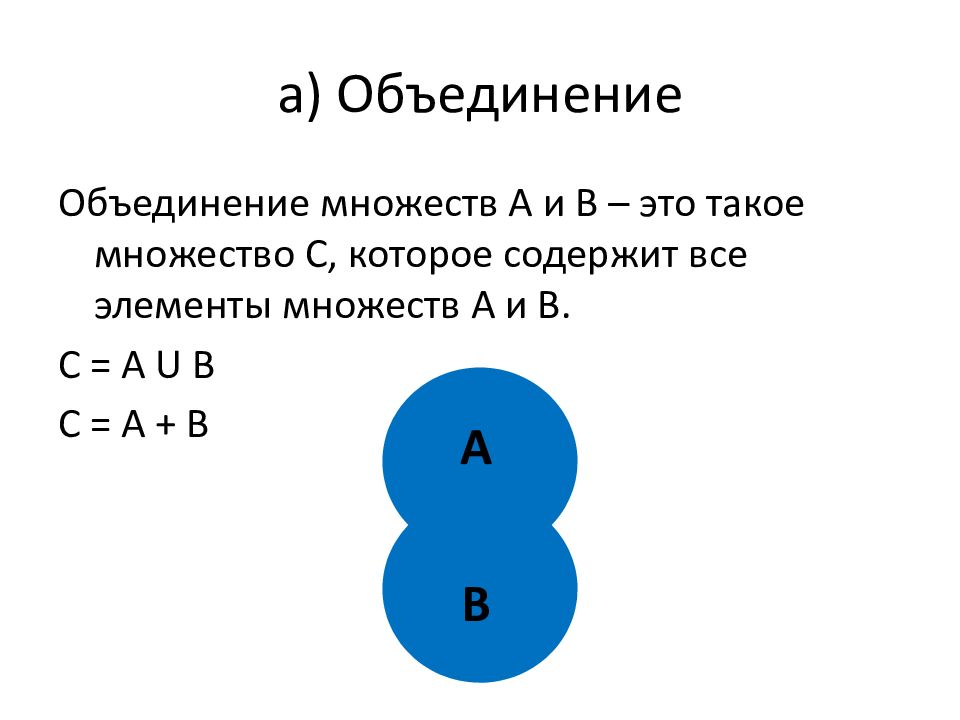
Объединение множеств А и В – это такое множество С, которое содержит все элементы множеств А и В. С = А U В С = А + В А В
Слайд 49: б) Пересечение
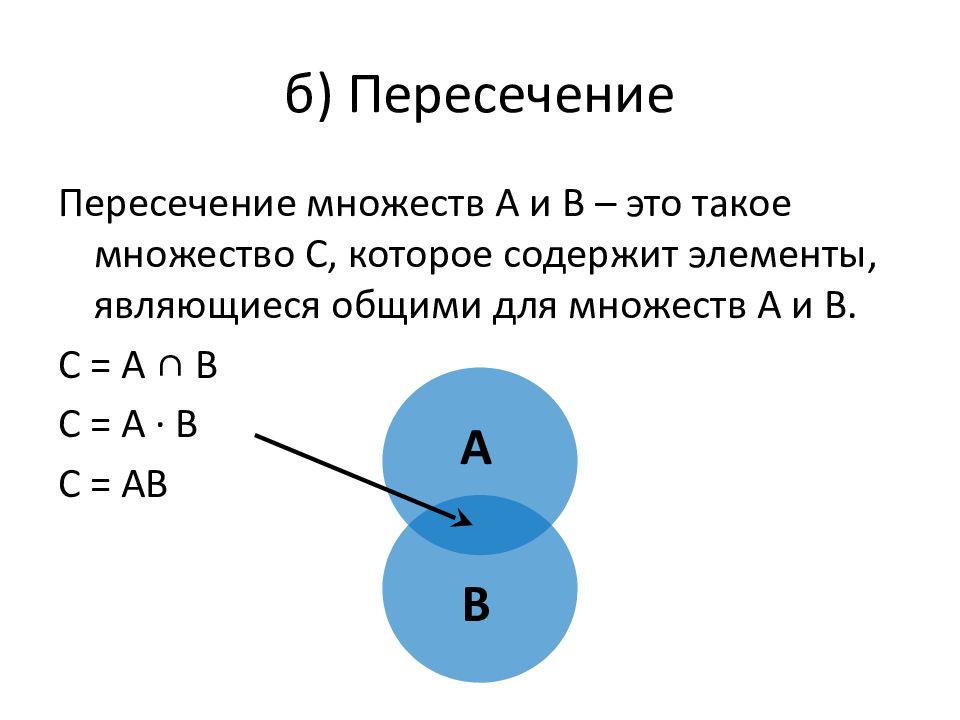
Пересечение множеств А и В – это такое множество С, которое содержит элементы, являющиеся общими для множеств А и В. С = А ∩ В С = А ∙ В С = АВ А В
Слайд 50: в) Разность
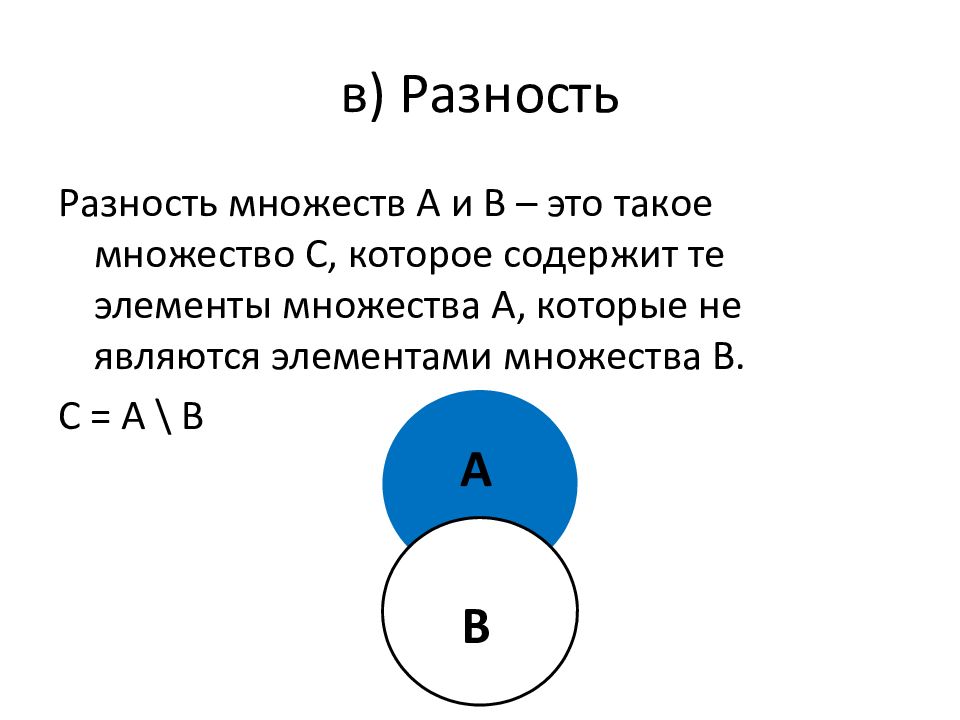
Разность множеств А и В – это такое множество С, которое содержит те элементы множества А, которые не являются элементами множества В. С = А \ В А В
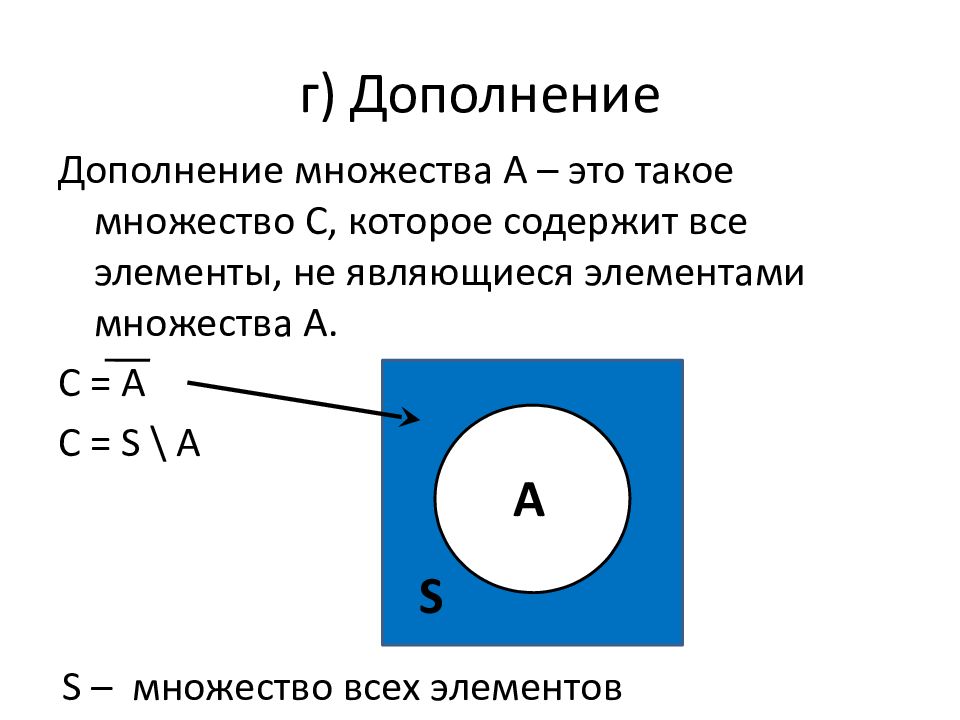
Слайд 51: г) Дополнение
Дополнение множества А – это такое множество С, которое содержит все элементы, не являющиеся элементами множества А. С = А С = S \ A А А S S – множество всех элементов
Слайд 53: Свойства операций над множествами
2. (А ∙ В) ∙ В = А ∙ В (1),(2) = > а) Добавление одного из множеств не меняет выражения. б) Логические уравнения нельзя «сокращать».
Слайд 54: Свойства операций над множествами
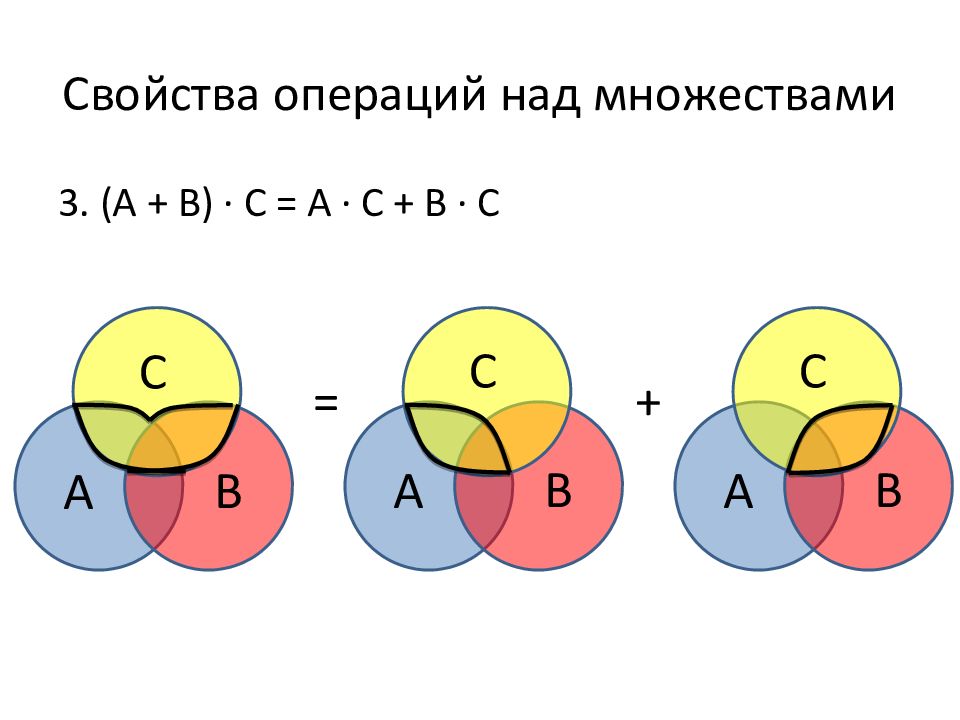
3. (А + В) ∙ С = А ∙ С + В ∙ С = + А В С А В С А В С
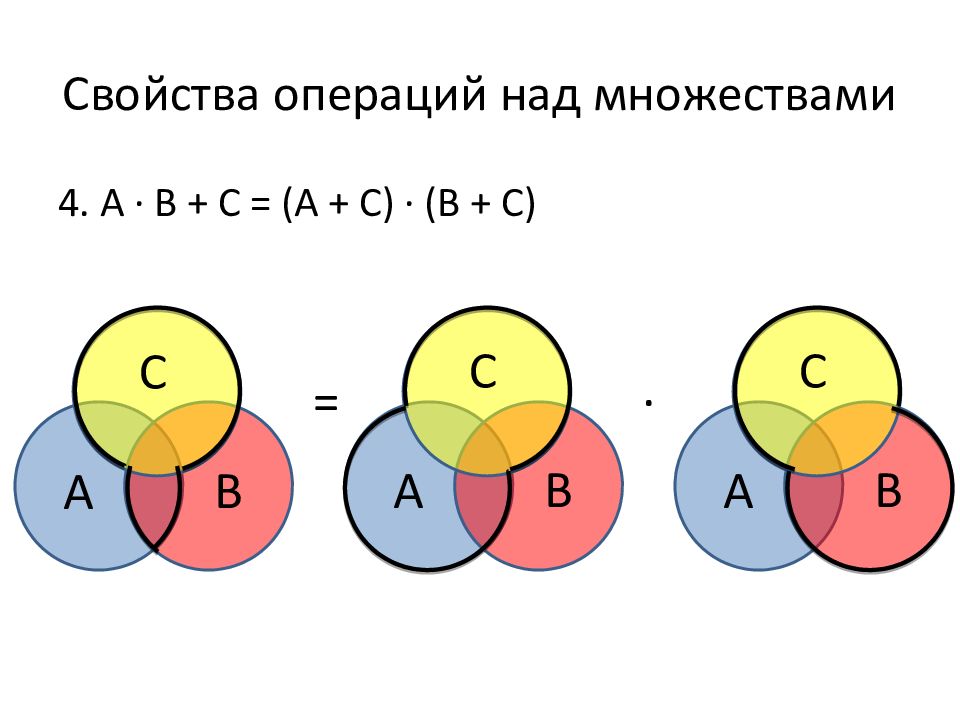
Слайд 55: Свойства операций над множествами
4. А ∙ В + С = (А + С) ∙ (В + С) = ∙ А В С А В С А В С
Слайд 60: 2.2. События
Каждое испытание приводит к некоторому исходу. Множество всех возможных исходов – пространство элементарных событий S. Событие – подмножество множества S, включающее в себя все исходы, удовлетворяющие некоторому критерию.
Слайд 61: Пример
Бросаем 2 кубика. S = { 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 2,1; …; 6,5; 6,6 } С1 – событие, когда сумма равна 8. С1 = { 2,6; 3,5; 4,4; 5,3; 6,2 } С2 – событие, когда на кубиках одинаковые числа. С2 = { 1,1; 2,2; 3,3; 4,4; 5,5; 6,6 } С1 ∙ С2 = {4,4 } ≠ 0 С1 и С2 – совместные события С1 + С2 = { 1,1; 2,2; 2,6; 3,3; 3,5; 4,4; 5,3; 5,5; 6,2; 6,6 } С3 – событие, когда сумма равна 7. С3 = { 1,6; 2,5; 3,4; 4,3; 5,2; 6,1 } С2 ∙ С3 = 0 С2, С3 – несовместные события
Слайд 62
Достоверное событие – событие, которое обязательно произойдёт ( U ). Невозможное событие – событие, которое не может произойти ( V). Случайное событие – событие, которое может произойти, а может не произойти.
Слайд 63
Если С1 ∙ С2 = V, то события несовместны. Если С1 ∙ С2 ≠ V, то события совместны. Если С1 ∙ С2 = V и С1 + С2 = S, то события противоположны. Противоположными называются 2 несовместных события, образующие полную группу случайных событий.
Слайд 64: Полная группа событий (ПГС)
ПГС – это такая группа случайных событий, что в результате опыта произойдёт хотя бы одно из них. Замечание. В ПГС могут присутствовать как несовместные, так и совместные события.
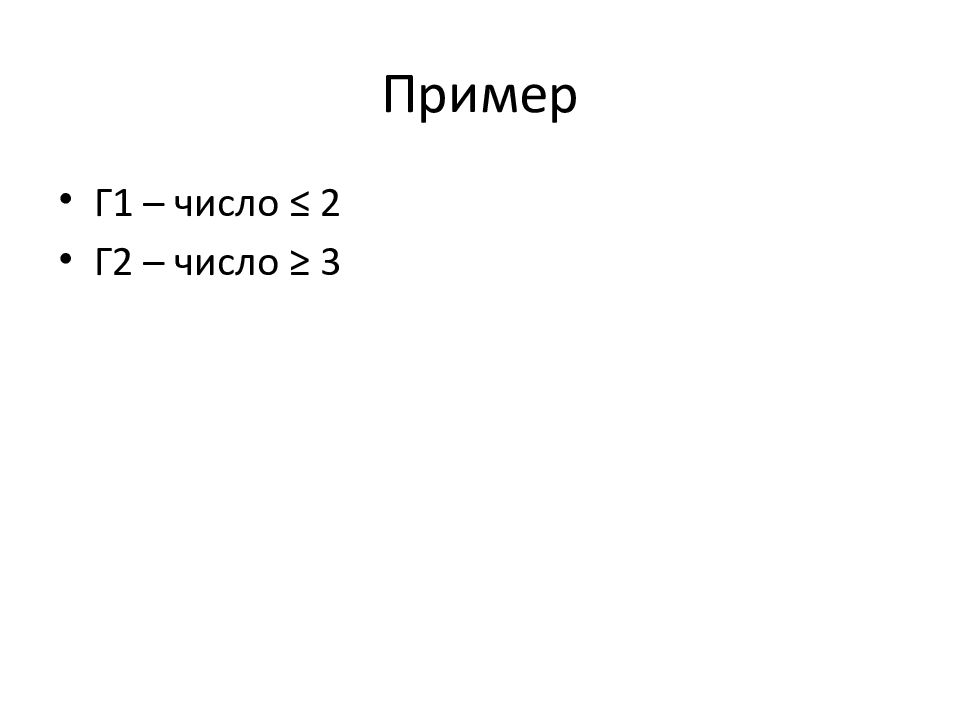
Слайд 65: Полная группа событий (ПГС)
Например, при бросании кубика обязательно произойдет одно из следующих событий: С1 – число ≤ 3 С2 – число ≥ 5 С3 – чётное число
Слайд 66: Группа гипотез
Группа гипотез – это такая ПГС, что в результате опыта произойдёт одно и только одно из событий. Замечание: 1) По сути группа гипотез – это полная группа несовместных событий. 2) Гипотезы не обязательно равновозможны.
Слайд 68
Гипотезы называются равновозможными, если нет оснований считать, что одна из них является более возможной, чем другая.
Слайд 69: 2.3. Вероятность
Вероятность – численная мера степени объективной возможности наступления случайного события. Обозначение: Р(А)
Слайд 70: Аксиомы вероятности
1. Р(А) – число от 0 до 1 2. Р( S) = 1; P(U) = 1; P(V) = 0 3. Если А и В несовместны, то Р(А + В) = Р(А) + Р(В) На основе этих аксиом строится вся теория вероятности. Из аксиомы 3 следует: Р(А) = 1 – Р(А)
Слайд 71: Как вычислить вероятность?
Есть 2 подхода: 1. На основе рассуждений ( априорные вероятности, то есть «до опыта»). 2. На основе опыта ( апостериорные вероятности, то есть «после опыта»).
Слайд 72: 1. Априорное (классическое) определение вероятности
Если результат опыта можно представить в виде группы равновозможных гипотез (исходов), то вероятность события А равна: Р(А) = m / n, где m – число исходов, благоприятствующих событию А; n – общее число всех возможных исходов.
Слайд 73: 2. Апостериорное (статистическое) определение вероятности
Вероятность события А равна: Р(А) = lim m / n n → ∞ где m – количество появлений события А; n – количество испытаний при достаточно большом их числе
Слайд 74: Условная вероятность
Пусть вероятность события А зависит от того, появилось или не появилось событие В. Такие события называются зависимыми. Такая вероятность называется условной : Р(А | В) - вероятность А при условии В или Р В (А) Формула для вычисления условной вероятности: Р(А | В) = Р(АВ) / Р(В)
Слайд 75: Независимые события
События называются независимыми, если наступление одного из них не изменяет вероятности второго. То есть, когда: Р(А | В) = Р(А)
Слайд 76: Умножение вероятностей
а) Независимые события Р(АВ) = Р(А) ∙ Р(В) Р(А 1 А 2 …А n ) = Р(А 1 ) ∙ Р(А 2 ) ∙ … ∙ Р(А n ) б) Зависимые события Р(АВ) = Р(А) ∙ Р( B|A) Р(А 1 А 2 …А n ) = Р(А 1 ) ∙ Р(А 2 |A 1 ) ∙ Р(А 3 |A 1 A 2 ) ∙ …
Слайд 77: Сложение вероятностей
а) Совместные и независимые события Р(А + В) = Р(А) + Р(В) – Р(АВ) Р(А + В + С) = = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(ВС) – Р(АС) + Р(АВС) Р(А + В + С + D ) = = Р(А) + Р(В) + Р(С) + Р( D ) – – Р(АВ) – Р( A С) – Р( AD ) – Р( BC ) – Р( BD ) – Р(С D ) + + Р(АВС) + Р(АВ D ) + Р( A С D ) + Р(ВС D ) – P(ABCD)
Слайд 78: Сложение вероятностей
б) Совместные и зависимые события Р(А + В) = Р(А) + Р(В) – Р(А) ∙ Р(В | А)
Слайд 79: Сложение вероятностей
в) Несовместные события Р(А + В) = Р(А) + Р(В) Р(А 1 + А 2 + … + А n ) = Р(А 1 ) + Р(А 2 ) + … + Р(А n )
Слайд 80: Сложение вероятностей
г) Противоположные события Р(А) + Р(А) = 1 д ) Группа гипотез Р(Н 1 ) + Р(Н 2 ) + … + Р(Н n ) = 1
Слайд 81: Формула полной вероятности
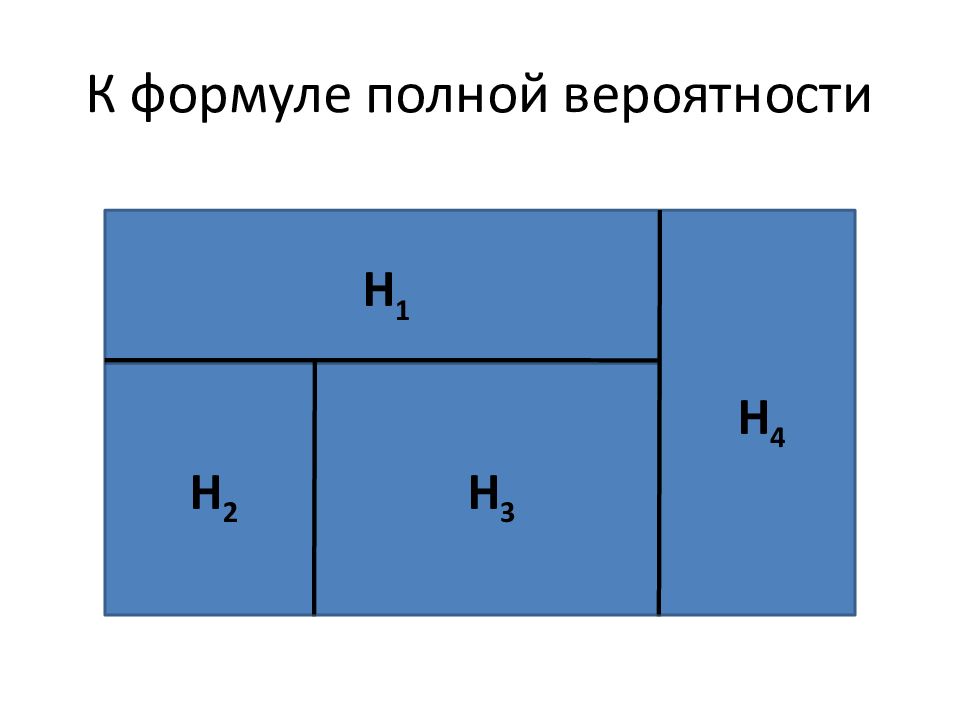
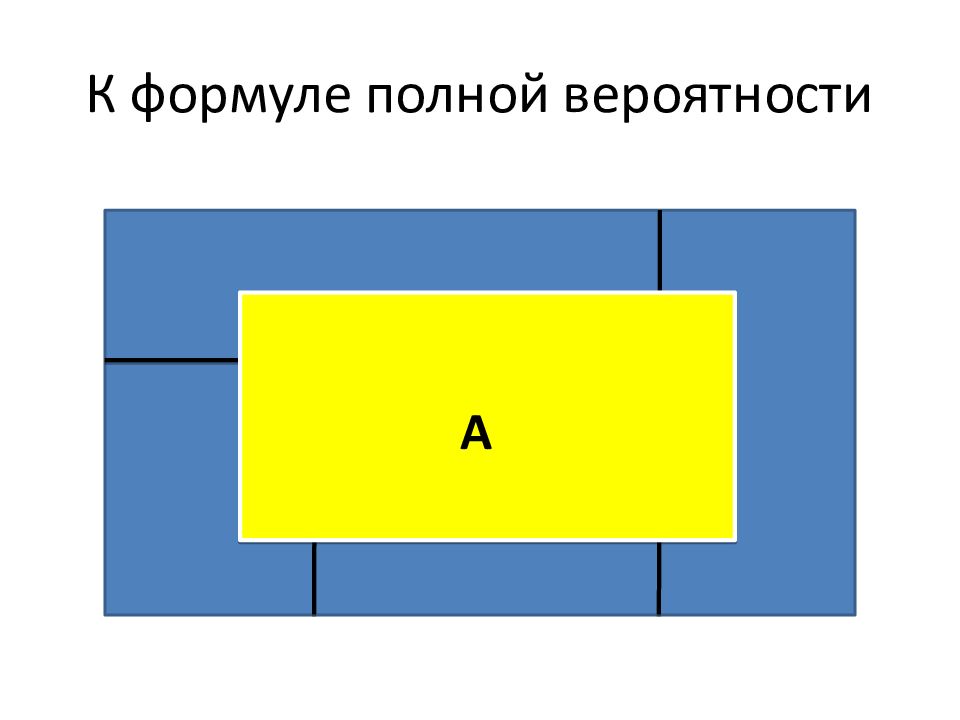
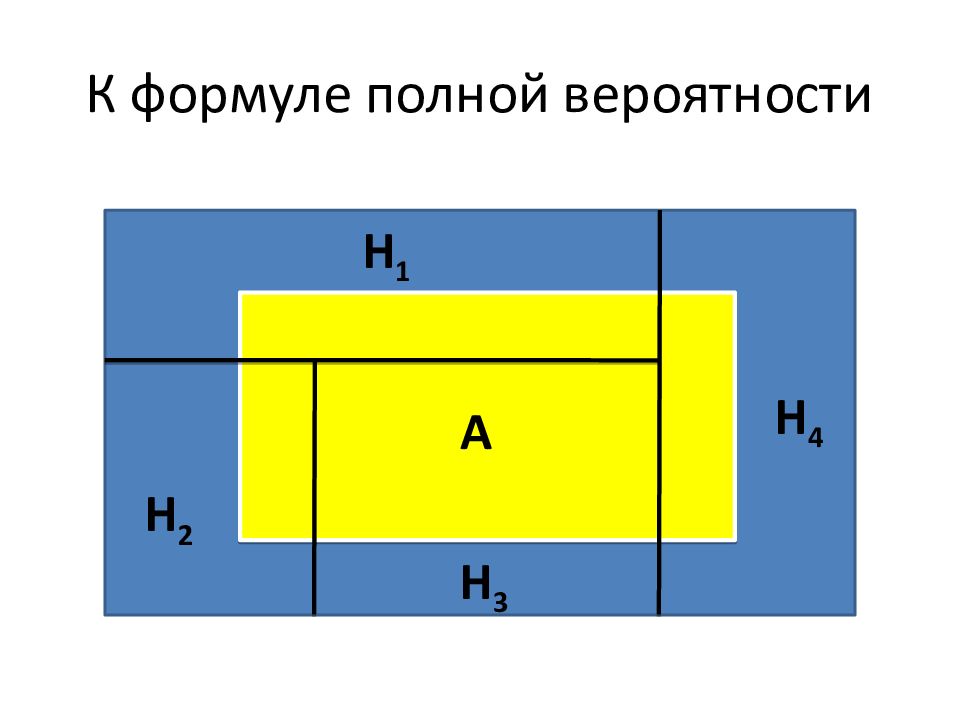
Пусть Н 1, Н 2, …, Н n – группа гипотез. Пусть событие А может наступить лишь при условии появления одной из гипотез. Тогда вероятность события А равна: Р(А) = Р(Н 1 )∙Р(А | Н 1 ) + Р(Н 2 )∙Р(А | Н 2 ) +…+ Р(Н n )∙Р(А | Н n )
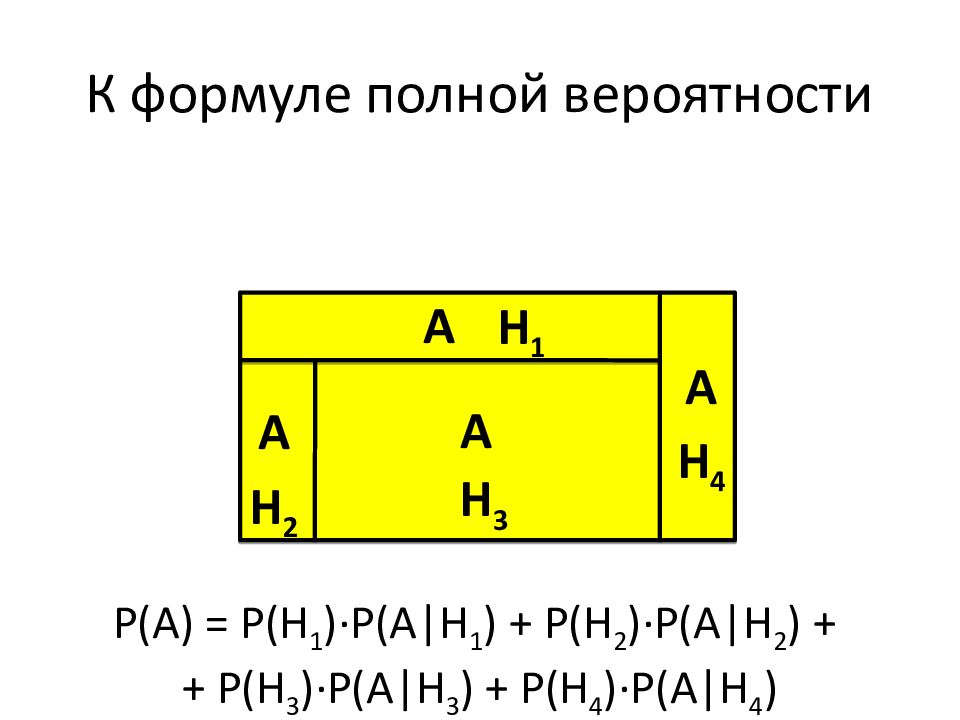
Слайд 85: К формуле полной вероятности
А Н 2 Н 3 Н 4 А А Н 1 А Р(А) = Р(Н 1 )∙Р(А | Н 1 ) + Р(Н 2 )∙Р(А | Н 2 ) + + Р(Н 3 )∙Р(А | Н 3 ) + Р(Н 4 )∙Р(А | Н 4 )
Слайд 86: Формула Байеса
Пусть Н 1, Н 2, …, Н n – группа гипотез. Пусть событие А может наступить лишь при условии появления одной из гипотез. Проведён опыт, в результате которого появилось событие А. Тогда вероятность того, что событие А произошло в результате определённой гипотезы Н i, равна:
Слайд 87
В формуле Байеса: Дано: Р(Н i ) – априорная вероятность гипотезы Н i (насколько вероятна причина вообще Н i, то есть до опыта); Р( A| Н i ) – вероятность события А при истинности гипотезы Н i. Найти: Р(Н i |A ) – апостериорная вероятность гипотезы Н i (насколько вероятна причина Н i с учетом факта происшедшего события А, то есть после опыта); Итак, формула Байеса позволяет переставить причину и следствие, то есть по известному факту события вычислить вероятность того, что оно было вызвано конкретной заданной причиной.
Слайд 88: Пример применения формулы Байеса
По линии связи посылаются сигналы 1 и 0 с вероятностями 0,6 и 0,4. Если посылается сигнал 1, то с вероятностями 0,9 и 0,1 принимаются сигналы 1 и 0. Если посылается сигнал 0, то с вероятностями 0,3 и 0,7 принимаются сигналы 1 и 0. Какова условная вероятность того, что посылается сигнал 1 при условии, что принимается сигнал 1?
Слайд 89: Решение
Рассматриваем гипотезы: Н1 – посылается сигнал 1; Р(Н1) = 0,6 Н2 – посылается сигнал 0; Р(Н2) = 0,4 Рассматриваем зависимые события: А|Н1 – принят сигнал 1 при условии, что послан сигнал 1; Р(А|Н1) = 0,9 А|Н2 – принят сигнал 1 при условии, что послан сигнал 0; Р(А|Н2) = 0,3 Н1|А – послан сигнал 1 при условии, что принят сигнал 1; Р(Н1|А) = ? По формуле Байеса:
Слайд 90: 2.4. Элементы комбинаторики
Перечислительная комбинаторика рассматривает задачи подсчёта количества различных конфигураций (например, перестановок, размещений, сочетаний и т.д.). Это нужно для расчета m и n в формуле априорной вероятности.
Слайд 91: 2.4.1. Перестановки
Перестановкой из n элементов называется всякий упорядоченный набор этих n элементов. Обозначим число перестановок n элементов П n. Пример: 123 132 213 231 312 321 П 3 = 6.
Слайд 93: 2.4.2. Сочетания
Пусть k ≤ n. Сочетанием из n элементов по k называется всякий неупорядоченный набор k элементов, выбранных из n данных элементов. Замечание: 2 сочетания являются одинаковыми, если имеют одинаковый состав элементов. При этом они могут иметь разный порядок этих элементов. Например, 12 = 21. Обозначим число сочетаний из n элементов по k : С n к. Пример: из элементов 1,2,3 берём сочетания по два элемента: 12 23 13 С 3 2 = 3.
Слайд 96: 2.4.3. Размещения
Пусть k ≤ n. Размещением из n элементов по k называется всякий упорядоченный набор k элементов, выбранных из n данных элементов. Замечание: 2 размещения являются разными, если имеют не только разный состав элементов, но и разный порядок этих элементов. Например, 12 ≠ 21. Обозначим число размещений из n элементов по k : А n к. Пример: из элементов 1,2,3 берём размещения по два элемента: 12 4) 21 23 5) 32 13 6) 31 А 3 2 = 6.
Слайд 98: 2.5. Случайные величины и их распределения
Случайной величиной называется величина, которая в результате испытания примет одно и только одно возможное значение, заранее неизвестное и зависящее от множества причин, которые заранее не могут быть учтены. Каждый исход испытания характеризуется случайной величиной. Х = {x 1, x 2, …} Случайные величины: ДСВ – дискретные НСВ - непрерывные
Слайд 99: Дискретная случайная величина
ДСВ – СВ, которая принимает отдельные изолированные возможные значения. Число возможных значений может быть конечным или бесконечным.
Слайд 100: Непрерывная случайная величина
НСВ – СВ, которая может принимать любые значения из конечного или бесконечного промежутка. Число возможных значений всегда бесконечно.
Слайд 101: 2.5.1. Числовые характеристики распределений
Закон распределения СВ полностью характеризует случайную величину. Но для решения многих задач достаточно использовать числовые характеристики случайной величины: математическое ожидание М; дисперсия D ; среднеквадратическое отклонение (СКО) σ.
Слайд 102: 1. Математическое ожидание
это наиболее вероятное, усредненное значение СВ. ДСВ: НСВ:
Слайд 103: 2. Дисперсия
это мера разброса СВ, то есть её усреднённое отклонение от математического ожидания. ДСВ: НСВ:
Слайд 104: Связь между математическим ожиданием и дисперсией
для ДСВ и НСВ: D(X) = M((X – M(X)) 2 ) D(X) = M(X 2 ) – (M(X)) 2
Слайд 105: 3. Среднеквадратическое отклонение
это также мера разброса СВ, но в отличие от дисперсии СКО измеряется в тех же единицах, что и сама СВ.
Слайд 106: Статистическое определение М, D
Если закон распределения СВ неизвестен, но имеется выборка значений СВ объёмом n, то можно приблизительно оценить математическое ожидание и дисперсию:
Слайд 107: Центрированная СВ
ЦСВ – это отклонение СВ от её математического ожидания Х = Х – М М(Х) = 0 D(X) = D(X)
Слайд 108: Нормированная СВ
это ЦСВ, выраженная в долях СКО. Z = X / σ М( Z) = 0 D(Z) = 1
Слайд 109: 2.5.2. Законы распределения вероятностей ДСВ
ДСВ задаётся: рядом распределения; функцией распределения (интегральный закон)
Слайд 110: а) Ряд распределения
это совокупность всех возможных значений х i дискретной СВ Х и соответствующих им вероятностей p i. Замечание: события х i образуют группу гипотез = > x i x 1 x 2 x n p i p 1 p 2 p n
Слайд 112: б) Функция распределения (интегральный закон)
это функция F(x), равная вероятности того, что СВ примет значение, не превышающее х. F(x) = P(X < х ) =
Слайд 113: Пример
Из 100 изделий, среди которых 10 дефектных, выбирают случайным образом 5 изделий. Построить ряд распределения дефектных изделий в данной выборке.
Слайд 114: 2.5.3. Законы распределения вероятностей НСВ
Задать НСВ таблицей нельзя. НСВ задают: функцией распределения F(x) (интегральный закон); плотностью распределения f(x) (дифференциальный закон).
Слайд 115: а) Интегральный закон распределения
Функция распределения – это вероятность того, что НСВ примет значение, меньшее х. F ( x ) = P ( X < x ) Свойства: Р ( а < Х < b ) = F ( b ) – F ( a ) F ( x 1 ) < F ( x 2 ) <=> x 1 < x 2 (функция F не убывает ) lim F ( x ) = 1 x → ∞ lim F ( x ) = 0 x → – ∞
Слайд 116: б) Дифференциальный закон распределения
Плотность распределения: Плотность распределения связана с функцией распределения:
Слайд 118: Некоторые дискретные распределения
Рассмотрим следующие распределения ДСВ: биномиальное (закон Бернулли); Пуассона (закон редких событий)
Слайд 119: 1) Биномиальное распределение
Теорема 4. Пусть р – вероятность события А. Тогда вероятность того, что из n независимых испытаний ровно k исходов будут благоприятны, равна: р n ( k ) = C n k p k (1 – p ) n – k - формула Бернулли.
Слайд 120: 1) Биномиальное распределение
Доказательство: Рассматривается 2 возможных исхода испытания: или появление, или отсутствие интересующего события А. Считаем, что испытания независимы. Пусть р – вероятность появления события А; р = const от опыта к опыту; Тогда (1 – р ) – вероятность отсутствия события А. Пусть из n исходов k – благоприятные, удачные.
Слайд 121: 1) Биномиальное распределение
Тогда вероятность пересечения k удачных и (n – k) неудачных будет равна: р k (1 – р ) n – k. При этом число способов, которыми из n исходов можно получить k удачных, равно:
Слайд 122: 1) Биномиальное распределение
Тогда вероятность того, что из n независимых испытаний k исходов будут благоприятны, равна: р n ( k ) = C n k p k (1 – p ) n – k
Слайд 123: 1) Биномиальное распределение
У биноминального распределения достаточно просто рассчитываются М и D : М = np D = np (1 – p)
Слайд 124: Пример на биномиальное распределение
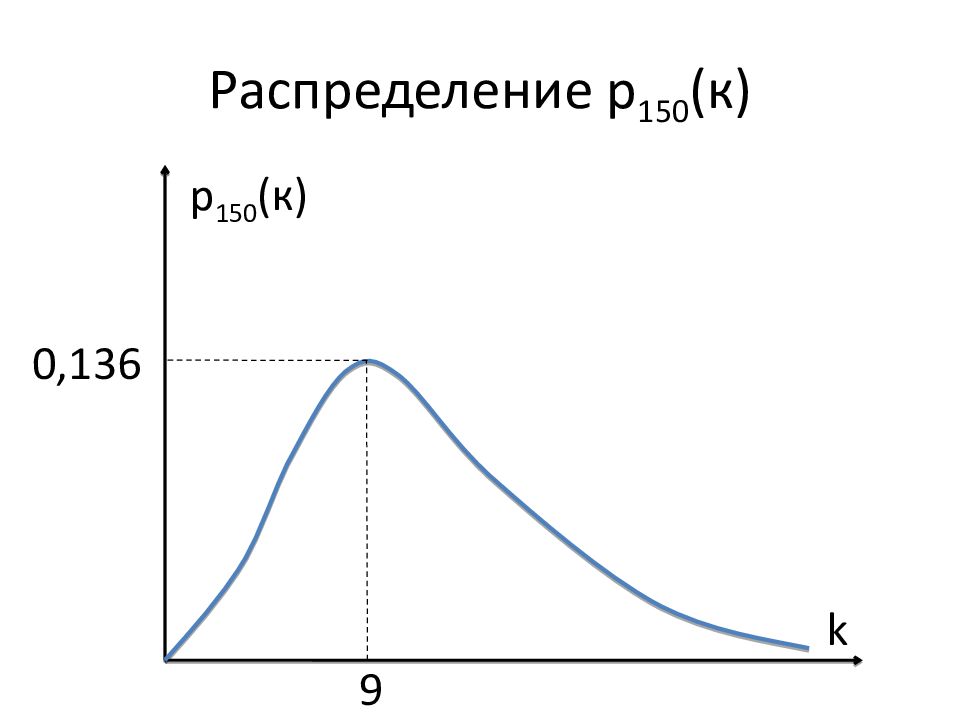
Энергосистема имеет 150 генераторных блоков. Вероятность отказа одного блока равна 0,06. а) Определить вероятность того, что в данный момент не работают ровно 2 блока. б) При каком числе k вероятность отказа одновременно k блоков будет максимальной? Определить эту вероятность.
Слайд 125: Решение
р = 0,06 1 – р = 1 – 0,06 = 0,94 р 150 ( 2 ) = C 150 2 ·0,06 2 ·0,94 150 – 2 = 0,00424. М = 150·0,06 = 9 = k D = 9·0,94 = 8,46 σ = 2,91 р 150 ( 9 ) = C 150 9 ·0,06 9 ·0,94 150 – 9 = 0,136.
Слайд 127: 2) Распределение Пуассона
Теорема 5. Пусть р – вероятность события А. При этом р – очень малое число. Проводится серия из n испытаний. Среднее число появления события А не меняется в различных сериях испытаний. а = np = const. Тогда вероятность появления k событий А равна
Слайд 128: 2) Распределение Пуассона
У распределения Пуассона достаточно просто рассчитываются М и D : М = D = а
Слайд 129: Пример
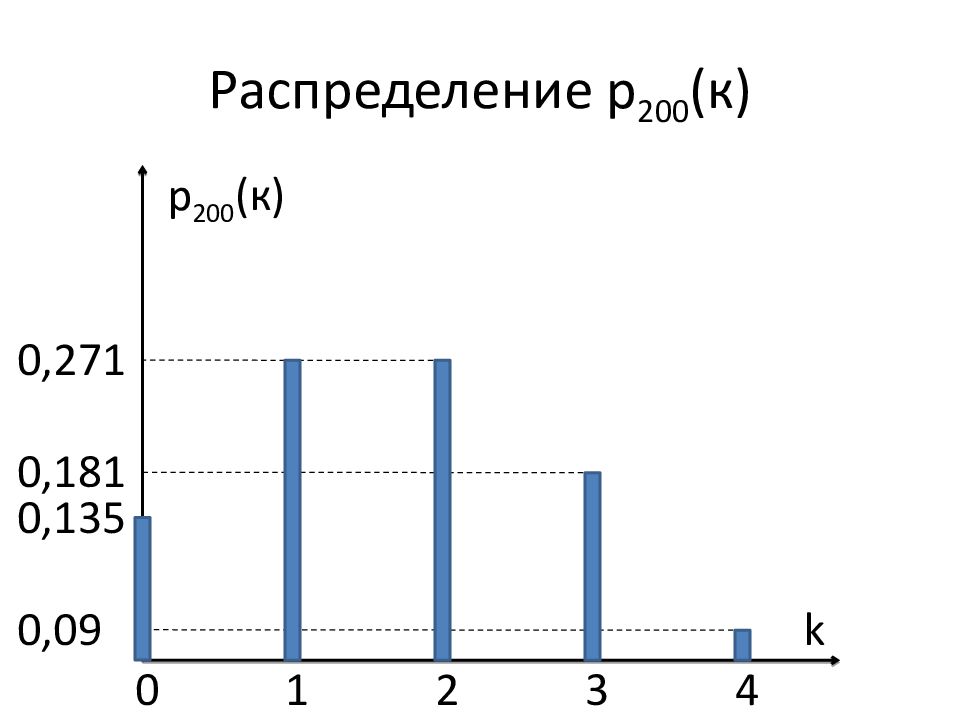
Завод производит реле с вероятностью дефекта 0,01. Покупаем 200 реле. Найти вероятность того, что среди купленных реле: не будет дефектных реле; будет 1 дефектное реле; будет 2 дефектных реле и т.д. Построить ряд распределения числа дефектных реле среди купленных.
Слайд 132: Некоторые непрерывные распределения
Рассмотрим следующие распределения НСВ: экспоненциальное; нормальное.
Слайд 133: 1) Экспоненциальное распределение
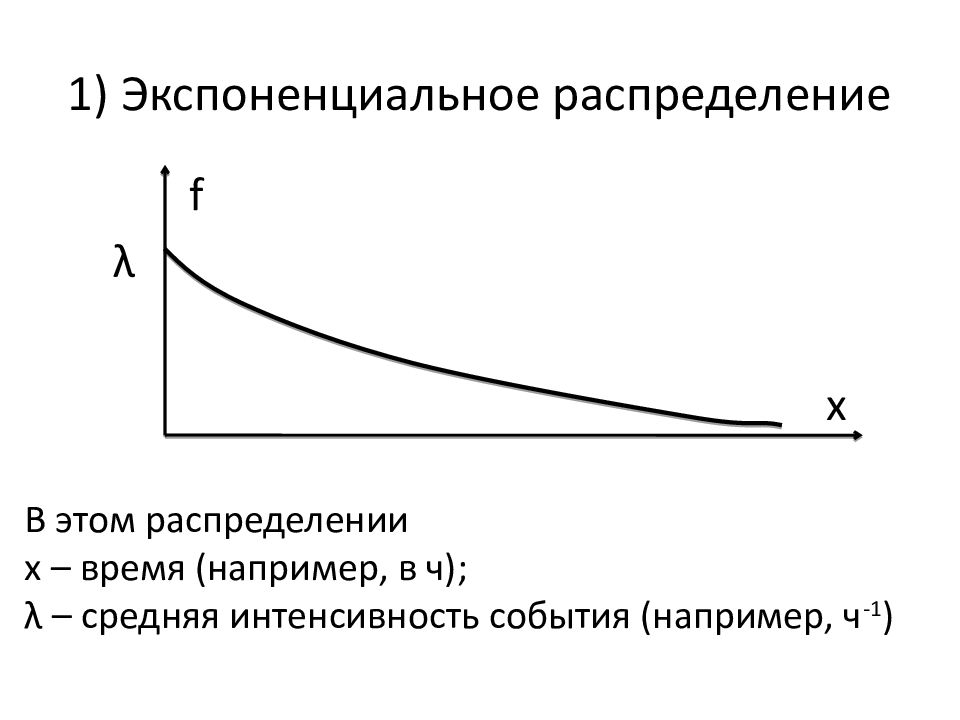
Задаётся плотность распределения: f(x) = λ exp(– λ x), где λ = const > 0 – единственный параметр распределения; х ≥ 0 Это распределение моделирует время между двумя последовательными совершениями одного и того же события.
Слайд 134: 1) Экспоненциальное распределение
f λ x В этом распределении х – время (например, в ч); λ – средняя интенсивность события (например, ч -1 )
Слайд 135: 1) Экспоненциальное распределение
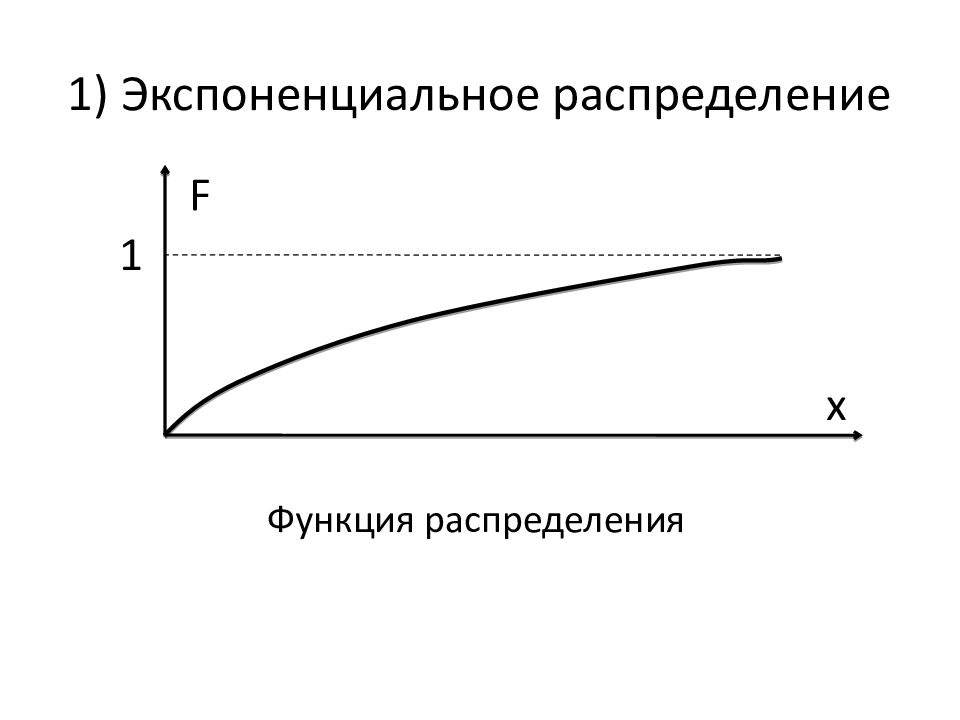
F(x) = 1 – exp(– λ x), М(Х) = 1/ λ D (Х) = 1/ λ 2
Слайд 137: Пример на экспоненциальное распределение
В среднем выключатель отказывает раз в 20 лет ( λ = 1/20). Тогда вероятность отказа выключателя: за 10 лет: 1 – exp( – 10 /20) = 0,39; за 20 лет: 1 – exp( – 2 0 /20) = 0,63; за 40 лет: 1 – exp( – 4 0 /20) = 0,86; за 60 лет: 1 – exp( – 6 0 /20) = 0,95.
Слайд 138: 2) Нормальное распределение
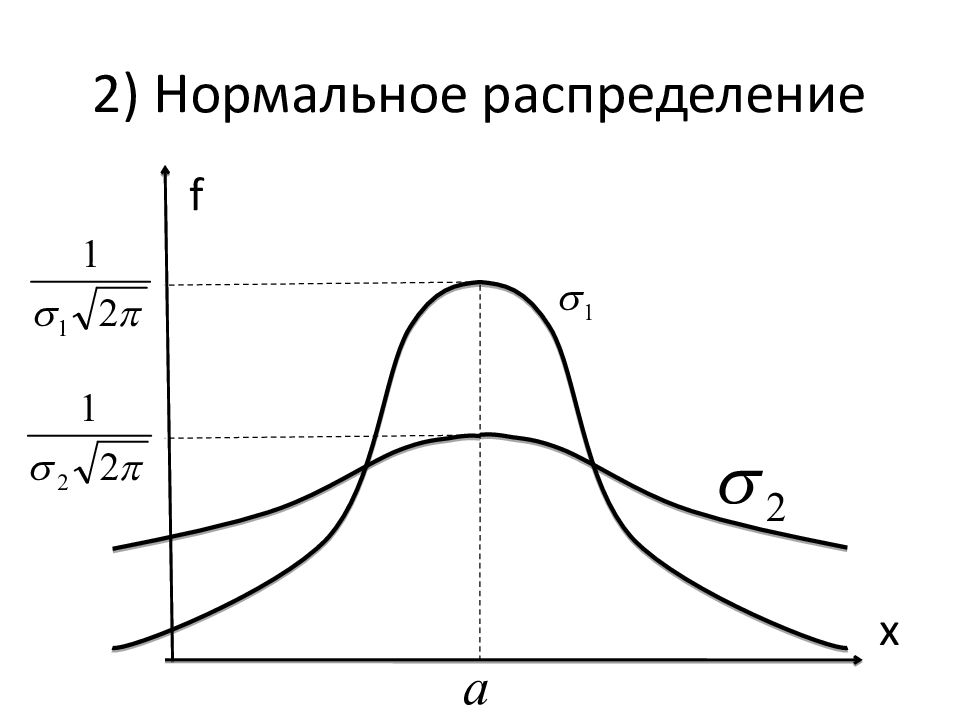
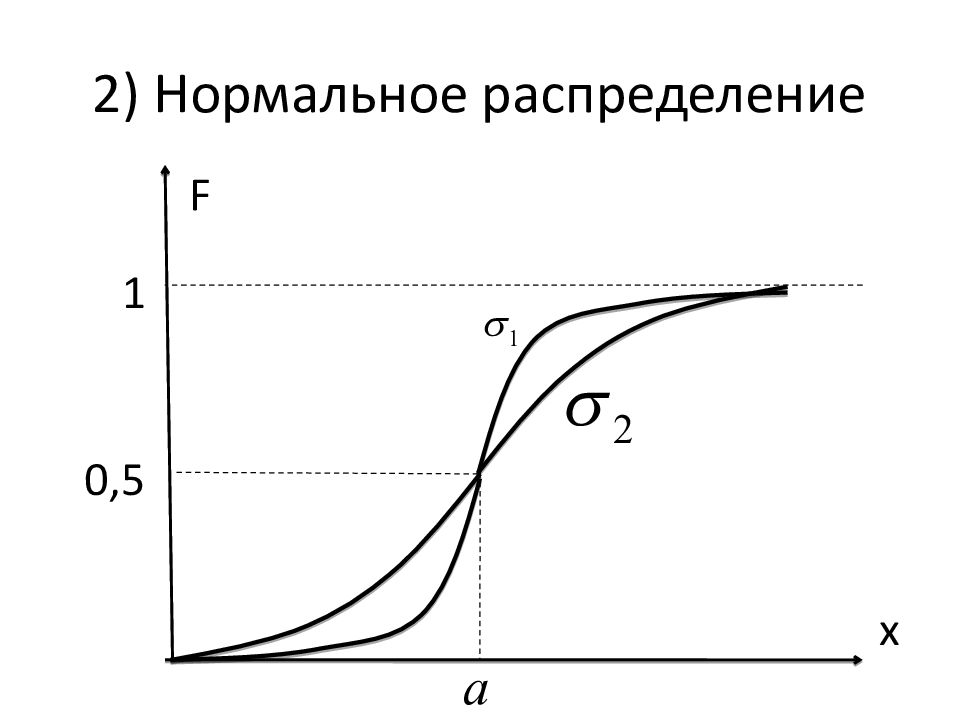
Плотность распределения: Функция распределения:
Слайд 139: 2) Нормальное распределение
В отличие от экспоненциального распределения (с единственным параметром λ ), характеризуется двумя параметрами: математическое ожидание a ; СКО σ.
Слайд 142: 2) Нормальное распределение
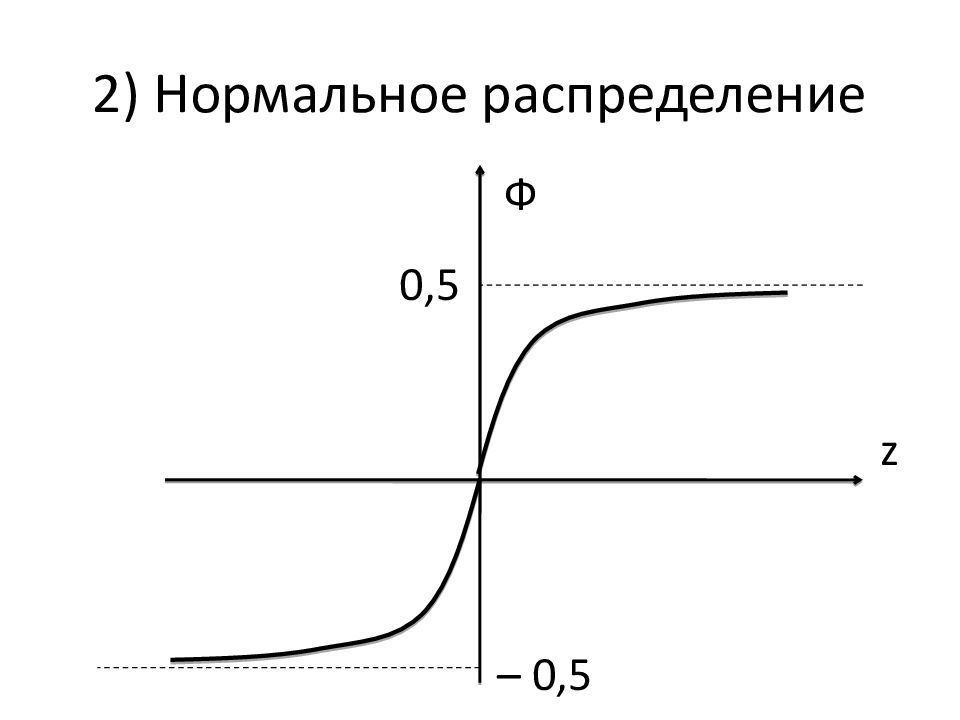
Видно, что: график f ( х ) симметричен относительно оси х = а ; график F(x) симметричен относительно точки ( а ; 0,5). Отсюда – идея центрировать эти функции: f ( х ), чтобы она стала чётной; F(x), чтобы она стала нечётной.
Слайд 143: 2) Нормальное распределение
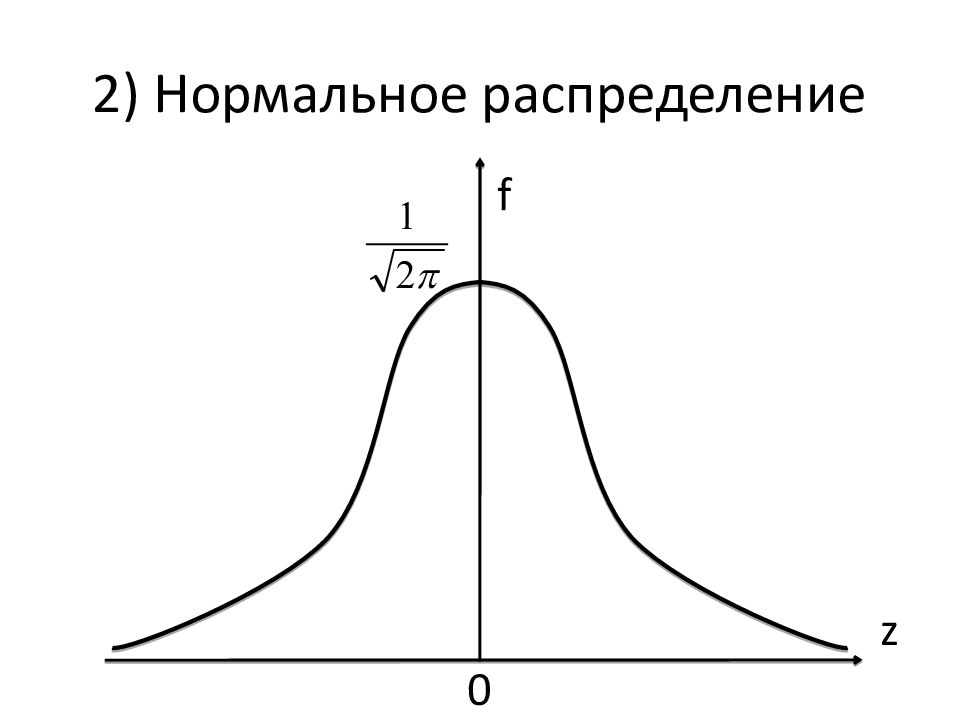
Пусть z = (x – a ) / σ. Этот аргумент – безразмерный, т.к. х, a, σ имеют одинаковые размерности. То есть функцию не только центрируют, но и нормируют.
Слайд 144: 2) Нормальное распределение
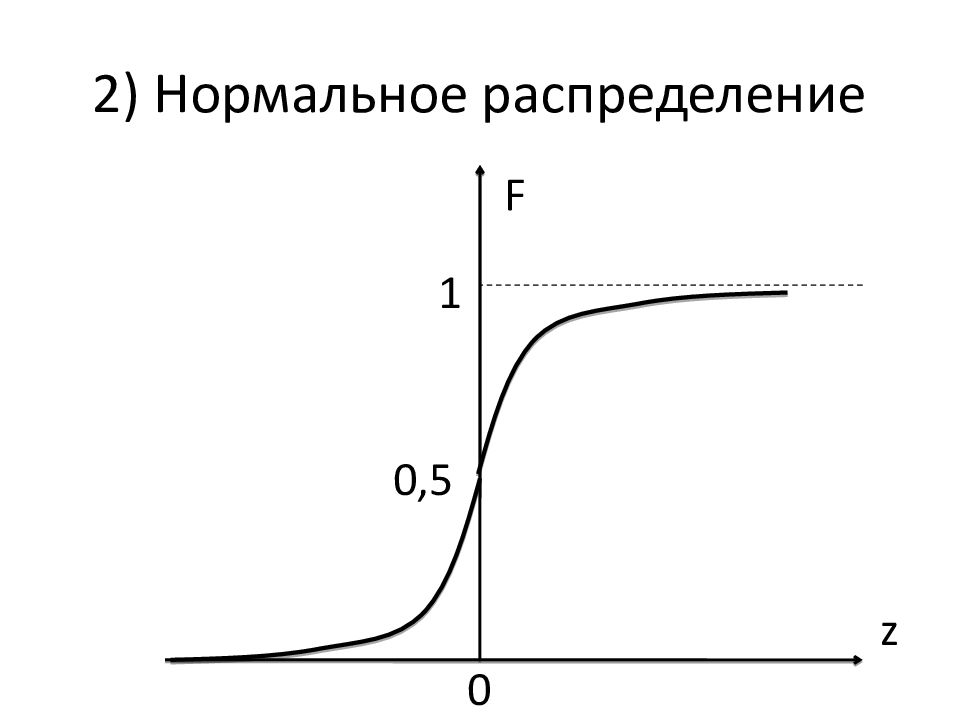
Плотность распределения: Функция распределения:
Слайд 147: 2) Нормальное распределение
Функция F(z) по-прежнему неудобна, т.к.: она не является ни чётной, ни нечётной; интеграл не берётся. Введём функцию Лапласа: Докажем, что F ( z) = 0,5 + Ф( z)
Слайд 149: 2) Нормальное распределение
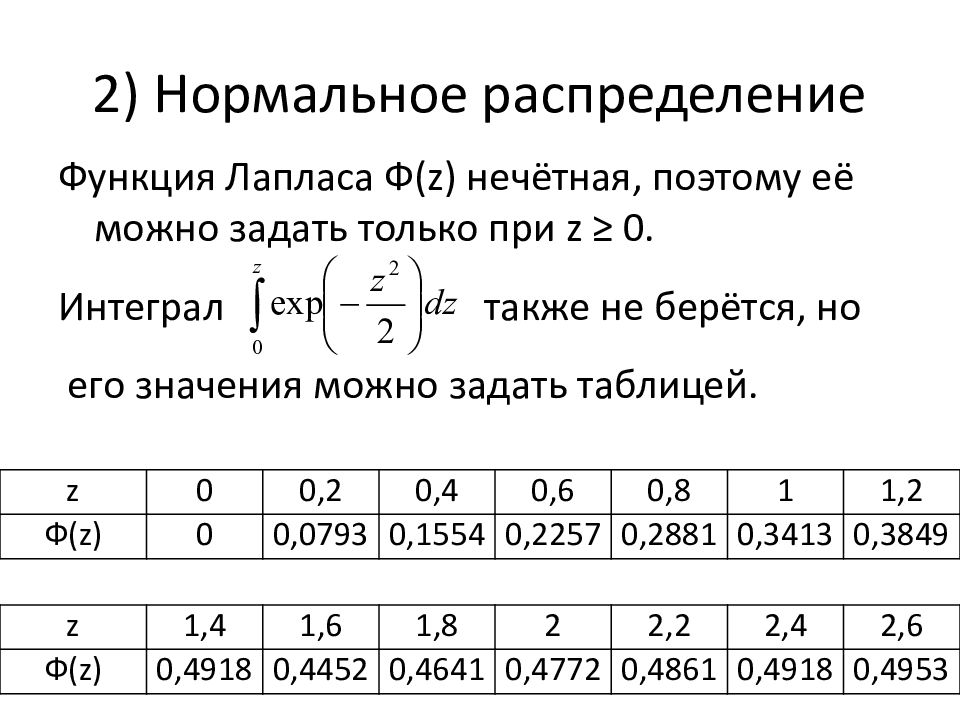
Функция Лапласа Ф (z) нечётная, поэтому её можно задать только при z ≥ 0. Интеграл также не берётся, но его значения можно задать таблицей. z 0 0,2 0,4 0,6 0,8 1 1,2 Ф( z) 0 0,0793 0,1554 0,2257 0,2881 0,3413 0,3849 z 1,4 1,6 1,8 2 2,2 2,4 2,6 Ф( z) 0,4918 0,4452 0,4641 0,4772 0,4861 0,4918 0,4953
Слайд 150: 2) Нормальное распределение
С помощью функции Лапласа можно вычислить вероятность того, что случайная величина примет значение между х 1 и х 2 : Р(х 1 < Х < х 2 ) = F( х 2 ) – F( х 1 ) = = 0,5 + Ф (z 2 ) – 0,5 – Ф (z 1 ) = Ф (z 2 ) – Ф (z 1 ), где z 1,2 = ( х 1,2 – а ) / σ
Слайд 151: Пример на вычисление вероятности для нормального распределения
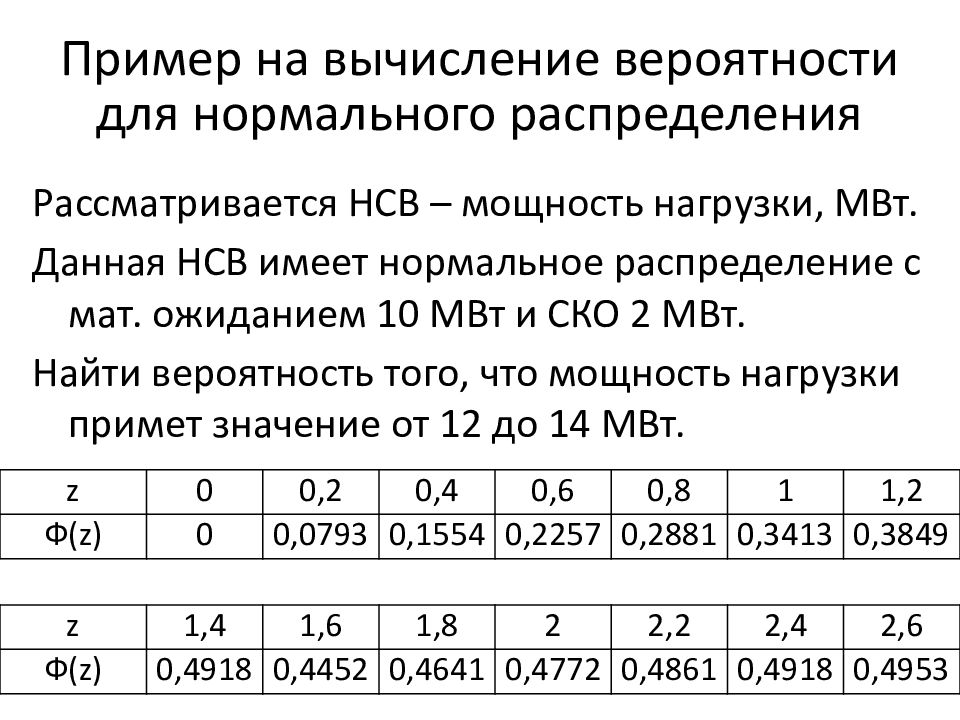
Рассматривается НСВ – мощность нагрузки, МВт. Данная НСВ имеет нормальное распределение с мат. ожиданием 10 МВт и СКО 2 МВт. Найти вероятность того, что мощность нагрузки примет значение от 12 до 14 МВт. z 0 0,2 0,4 0,6 0,8 1 1,2 Ф( z) 0 0,0793 0,1554 0,2257 0,2881 0,3413 0,3849 z 1,4 1,6 1,8 2 2,2 2,4 2,6 Ф( z) 0,4918 0,4452 0,4641 0,4772 0,4861 0,4918 0,4953
Слайд 152: Пример на вычисление вероятности для нормального распределения
Решение: z 1 = ( х 1 – а ) / σ = (12 – 10 ) / 2 = 1; z 2 = (х 2 – а ) / σ = (14 – 10 ) / 2 = 2; Р(12 < Х < 14) = Ф ( 2 ) – Ф ( 1 ) = 0,4772 – 0,3413 = = 0,1359.
Слайд 153: Глава 3. Показатели надежности
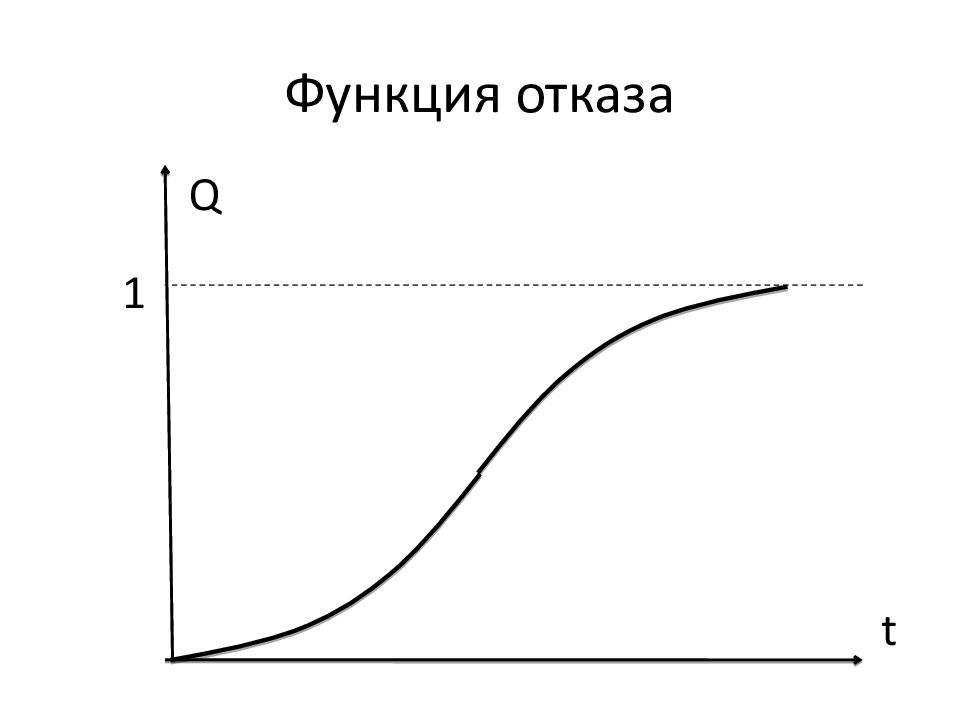
3.1. Невосстанавливаемые объекты Пусть при t = 0 объект начинает работу; при t = Т происходит отказ объекта. Т – НСВ, которая называется наработка до отказа. Обозначим функцию распределения этой НСВ Q(t). Назовём Q(t) функцией отказа. По определению: Q(t) = P(T < t) – вероятность отказа объекта до момента t.
Слайд 155
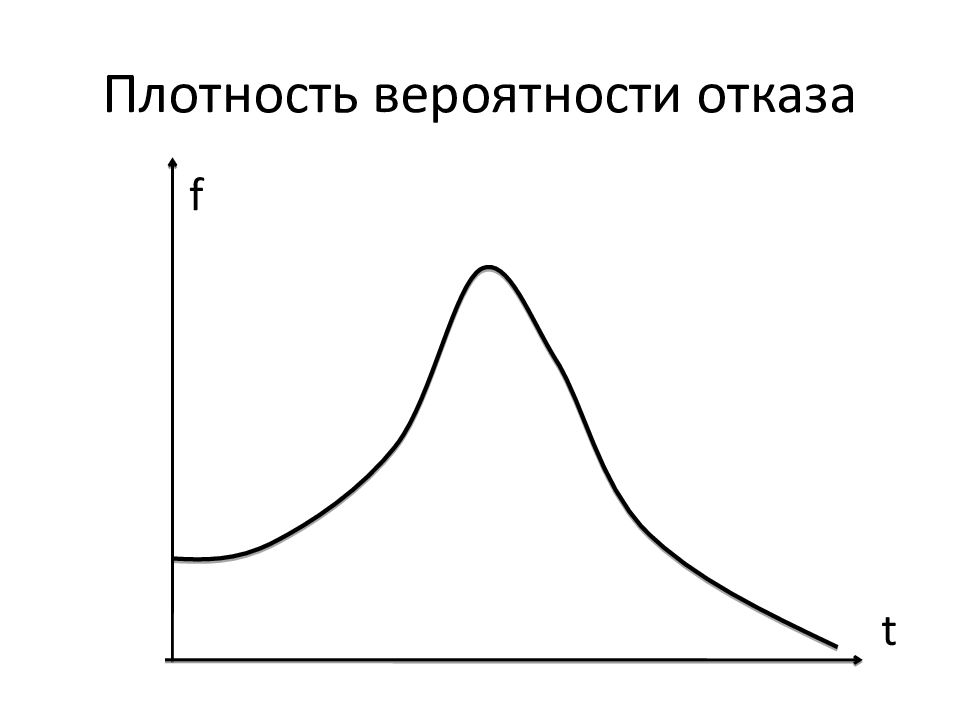
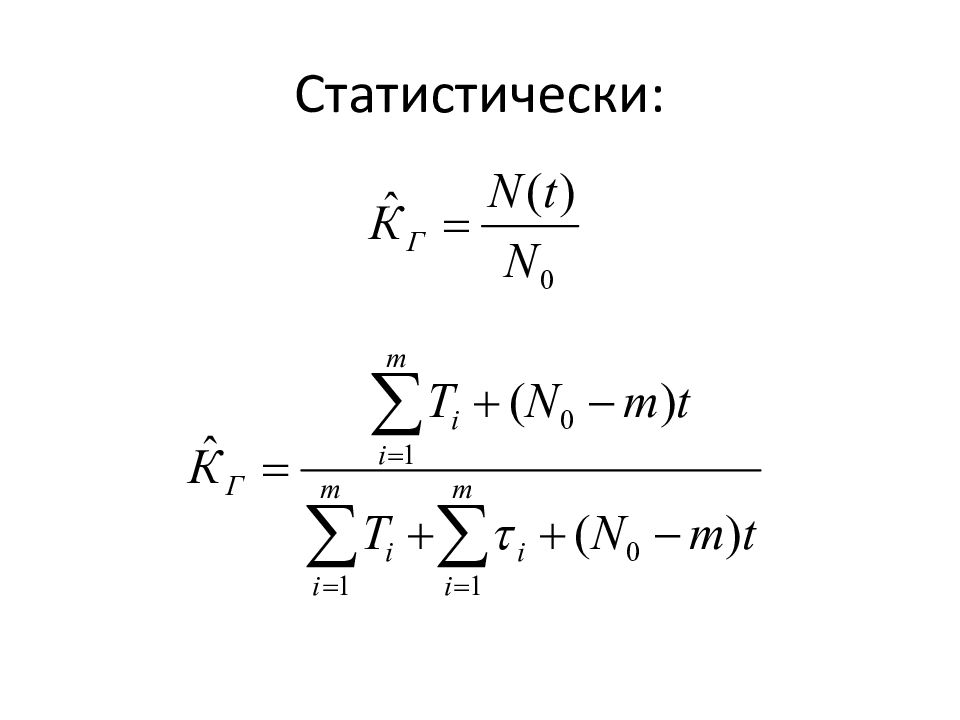
Введем понятие плотности вероятности отказа объекта f(t). Аналитически: f(t) = Q’(t). Статистически: где m(t) – количество объектов, отказавших к моменту времени t ; N(t) – количество объектов, исправных к моменту времени t ; N 0 – количество объектов, исправных при t = 0.
Слайд 157
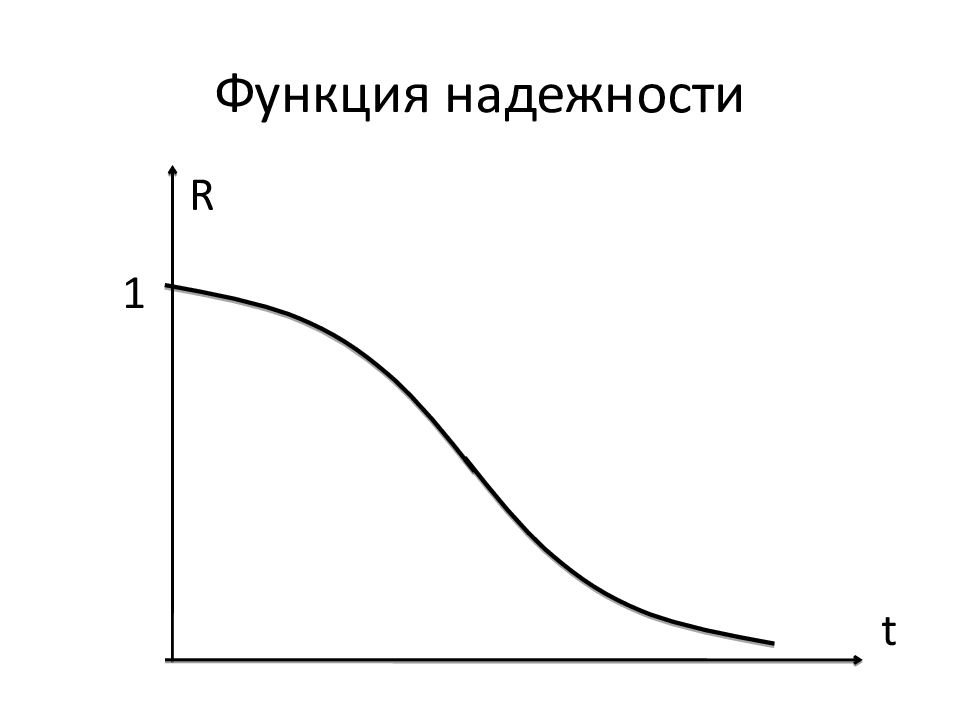
Обозначим вероятность безотказной работы в течение времени t : R(t) = P(T > t) Назовём R(t) функцией надежности. Аналитически: R(t) = 1 – Q(t). Статистически:
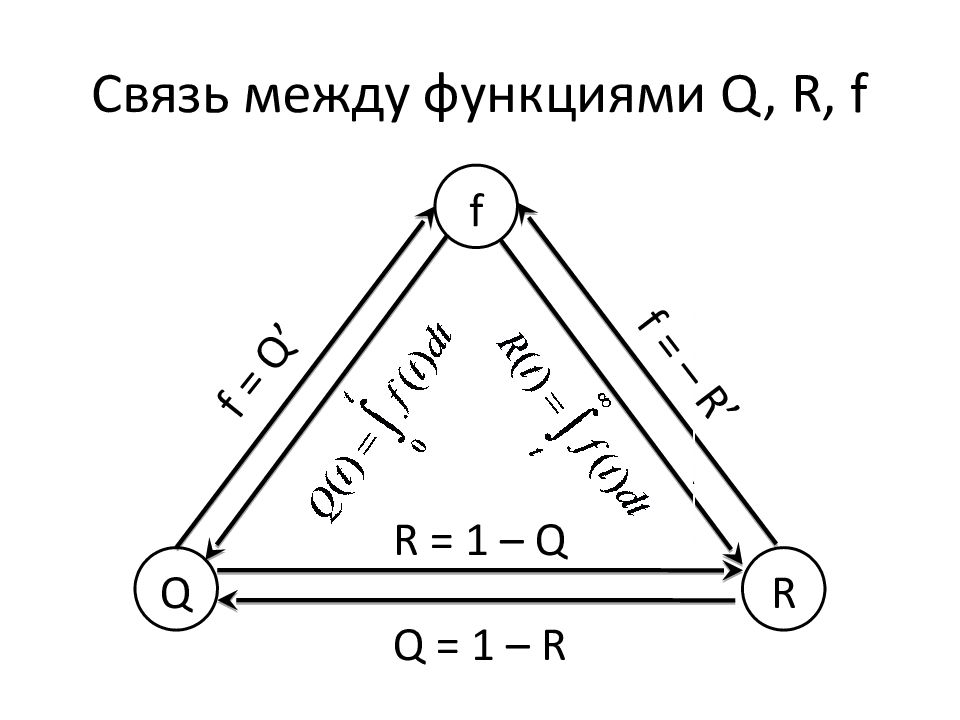
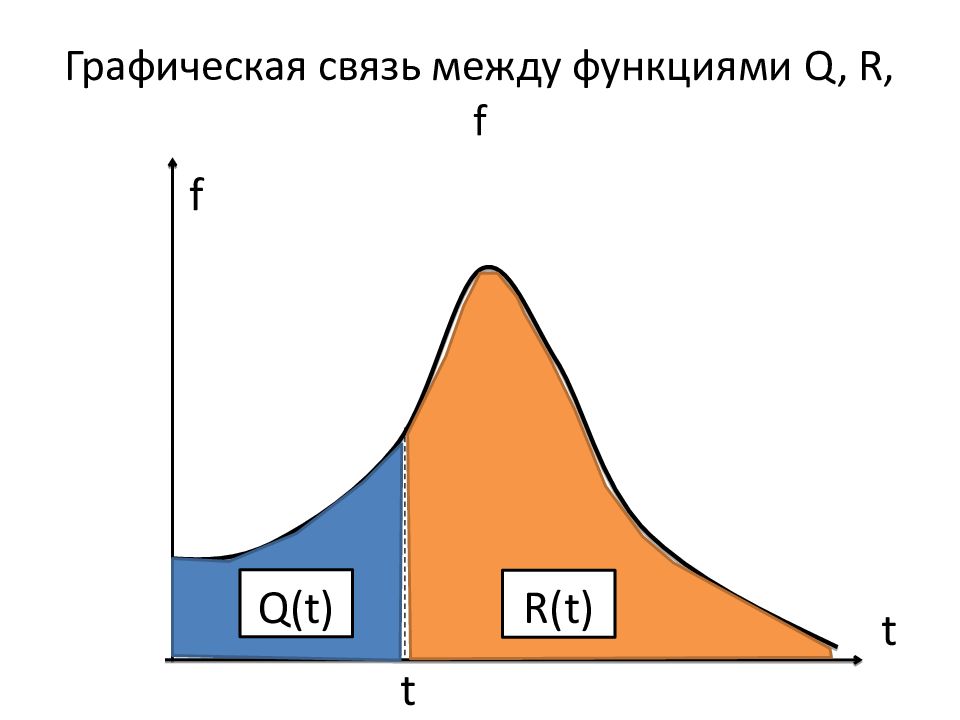
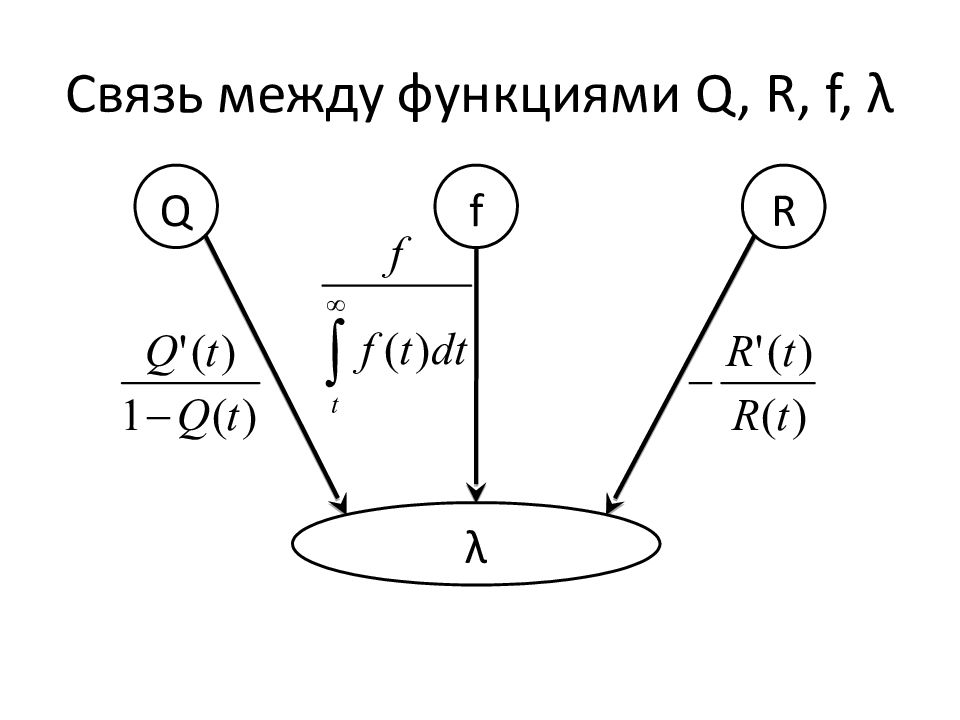
Слайд 159: Связь между функциями Q, R, f
Q R f Q = 1 – R R = 1 – Q f = Q’ f = – R’
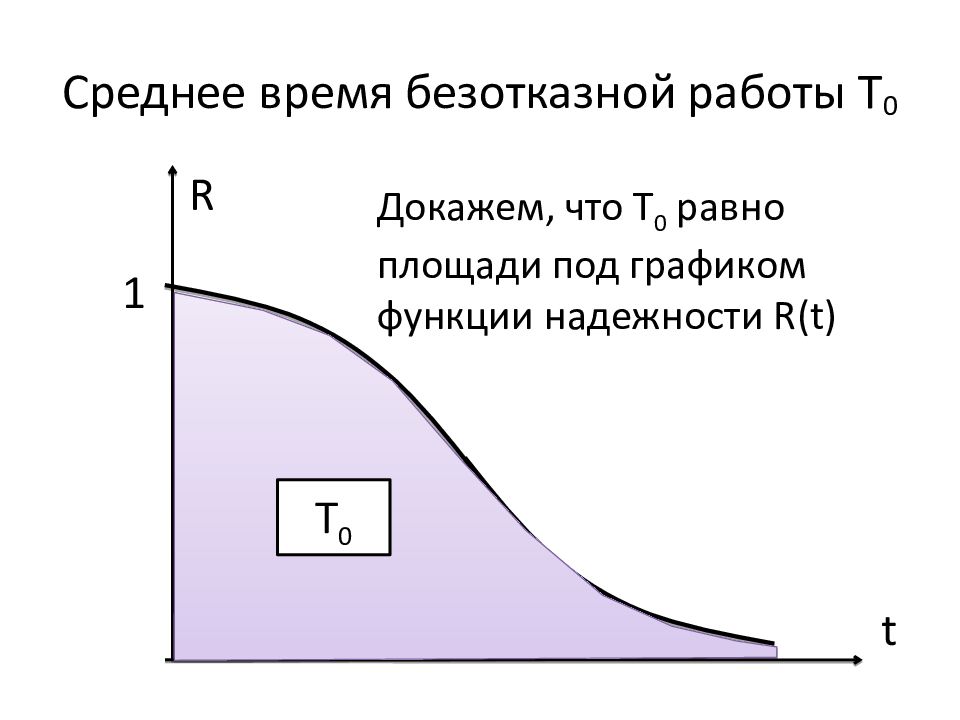
Слайд 161: Среднее время безотказной работы Т 0
R t 1 Т 0 Докажем, что Т 0 равно площади под графиком функции надежности R(t)
Слайд 162: Среднее время безотказной работы Т 0
Статистически: где t i – наработка до отказа i - го объекта; N 0 – первоначальное количество исправных объектов. Причём испытания проводят, пока все N 0 объектов не откажут.
Слайд 163: Среднее время безотказной работы Т 0
Если нет возможности дожидаться отказа всех объектов (из-за недостатка времени), то Т 0 можно оценить так: где t – время испытания; m – число отказавших объектов за время t
Слайд 164: Интенсивность отказов λ ( t)
[ λ ] = с -1, ч -1, год -1 и т. д. Статистически: λ ( t) – число отказов в единицу времени, отнесённое к числу безотказно проработавших до этого времени объектов. С позиций теории вероятности: λ ( t) – условная плотность вероятности отказа объекта при условии, что до рассматриваемого момента отказа не было. Таким образом λ ( t) является локальной характеристикой надёжности, т.е. определяет надёжность объекта в каждый данный момент времени.
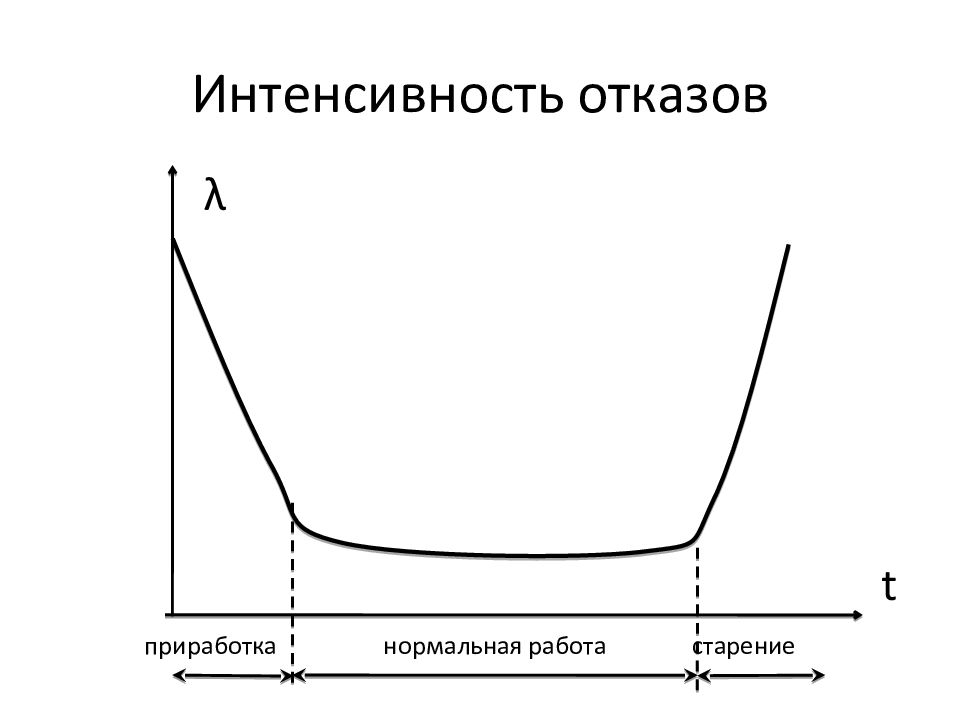
Слайд 165: Интенсивность отказов λ ( t)
Аналитически: Статистически: где m ( Δ t) – количество отказов за время Δ t.
Слайд 168
Для нормальной работы можно считать: λ ( t) = const = λ Тогда R(t) = exp(– λ t) Q(t) = 1 – exp(– λ t) f(t) = λ exp(– λ t) T 0 = 1 / λ Получили экспоненциальный закон распределения с параметром λ.
Слайд 169
При экспоненциальном законе вероятность безотказной работы на интервале ( t; t + Δ t) не зависит от времени предшествующей работы t, а зависит только от продолжительности интервала Δ t. Доказательство: R(t; t + Δ t) = exp(– λΔ t) По формуле условной вероятности R(t; t + Δ t) = R(t + Δ t) / R(t) = = exp(– λ (t + Δ t) ) / exp(– λ t) = = exp(– λ (t + Δ t) + λ t)
Слайд 170: Упрощение формул для малых времён t
В практических расчетах при малых временах рассмотренные выше формулы упрощают, используя соотношение из теории эквивалентов: exp(x) ~ 1 + x при х → 0 Тогда R(t) = 1 – λ t R(t; t + Δ t) = 1 – λΔ t Q(t) = λ t Эти зависимости верны для малых λ t (т.е. t << T 0 ).
Слайд 171: 3.2. Объекты с мгновенным восстановлением
Эксплуатация восстанавливаемого объекта не прекращается при его отказе. Объект ремонтируется или заменяется новым. Наработка между отказами и продолжительность восстановления являются НСВ. Рассмотрим ситуацию, когда время восстановления << наработки между отказами.
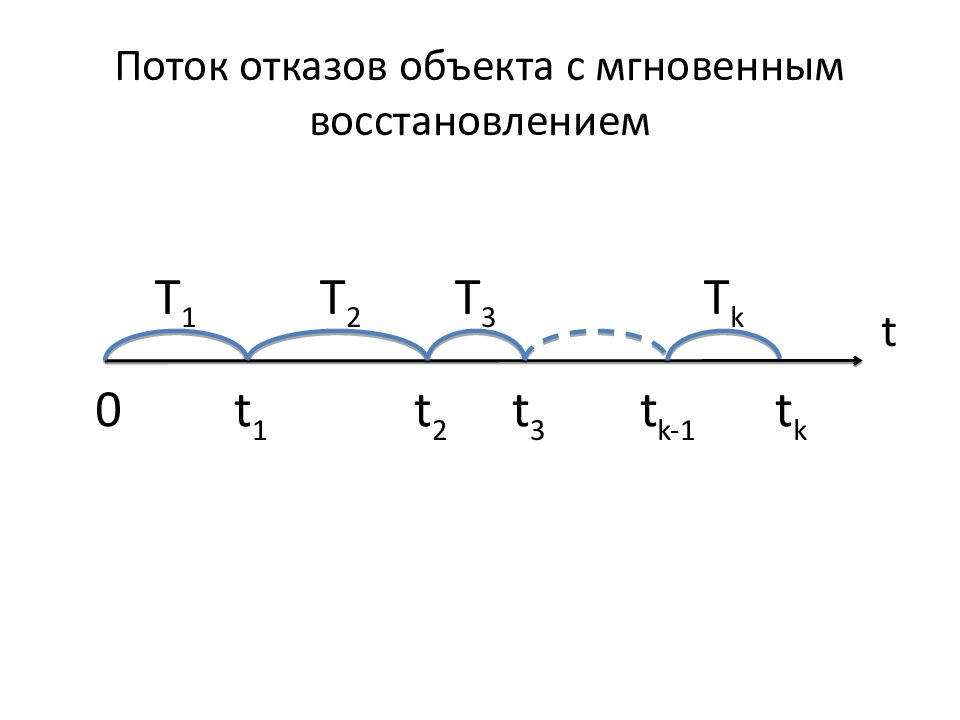
Слайд 172: Поток отказов объекта с мгновенным восстановлением
t Т 1 Т 2 Т 3 Т k t 1 t 2 t 3 t k t k-1 0
Слайд 173: Рассмотрим плотности вероятностей времени:
до первого отказа f 1 (t); до второго отказа f 2 (t); … до k- го отказа f k (t). Пусть первый отказ произошёл в момент τ ; пусть второй отказ произошёл в момент t.
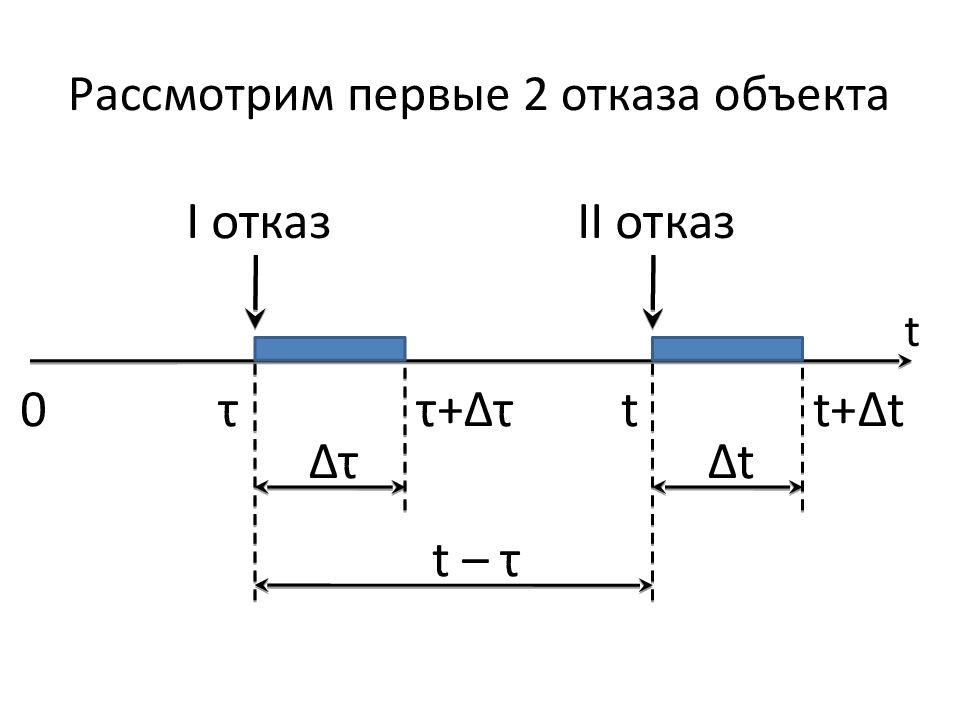
Слайд 174: Рассмотрим первые 2 отказа объекта
t I отказ τ τ + Δτ Δτ t+ Δ t t 0 II отказ Δ t t – τ
Слайд 175: Выведем формулу для f 2 (t)
Наработка на второй отказ равна t – τ. Рассмотрим вероятность того, что второй отказ произойдёт на интервале ( t; t + Δ t): Δ f 2 ( t ) Δ t = f 1 ( τ ) Δτ ∙ f 1 ( t – τ ) Δ t Разделим на Δ t и проинтегрируем по τ от 0 до t :
Слайд 176: Обобщим этот результат на k отказов. Выведем формулу для f k (t)
Пояснение: Дошли до ( k – 1) -го отказа, зафиксировали накопившуюся вероятность и начали отсчёт времени с нуля. Значит, следующий отказ будет первым => => в интеграле имеется f 1 (t).
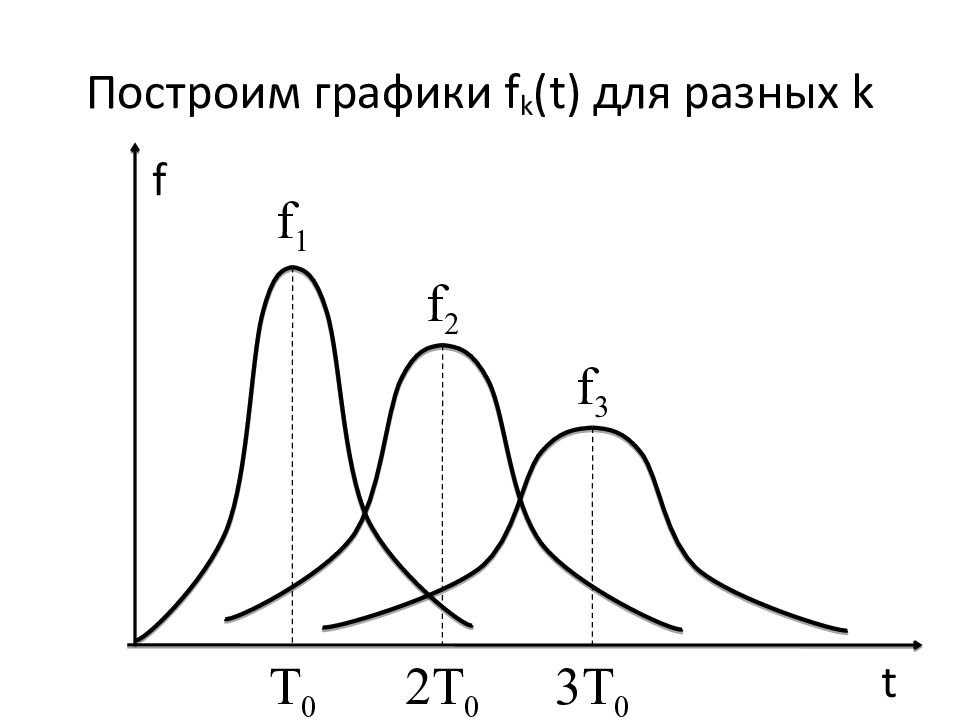
Слайд 178: Свойства графиков f k (t)
Каждый график f k (t) имеет максимум в точке t = k Т 0. Каждый график f k (t) приблизительно симметричен относительно оси t = k Т 0. Максимальное значение функции f k (t) уменьшается с ростом k, т.к. накапливаются неопределённости по предыдущим наработкам. Кривая f k (t) становится более пологой (широкой) с ростом k.
Слайд 179: Параметр потока отказов ω ( t)
Назовём сумму f 1 (t) + f 2 (t) + … + f k (t) = ω (t) параметром потока отказов. По сути ω (t) – это плотность вероятности отказа. С одной стороны функция ω (t) является локальной по времени, с другой стороны она охватывает одновременно все отказы, т.е. является глобальной по отказам.
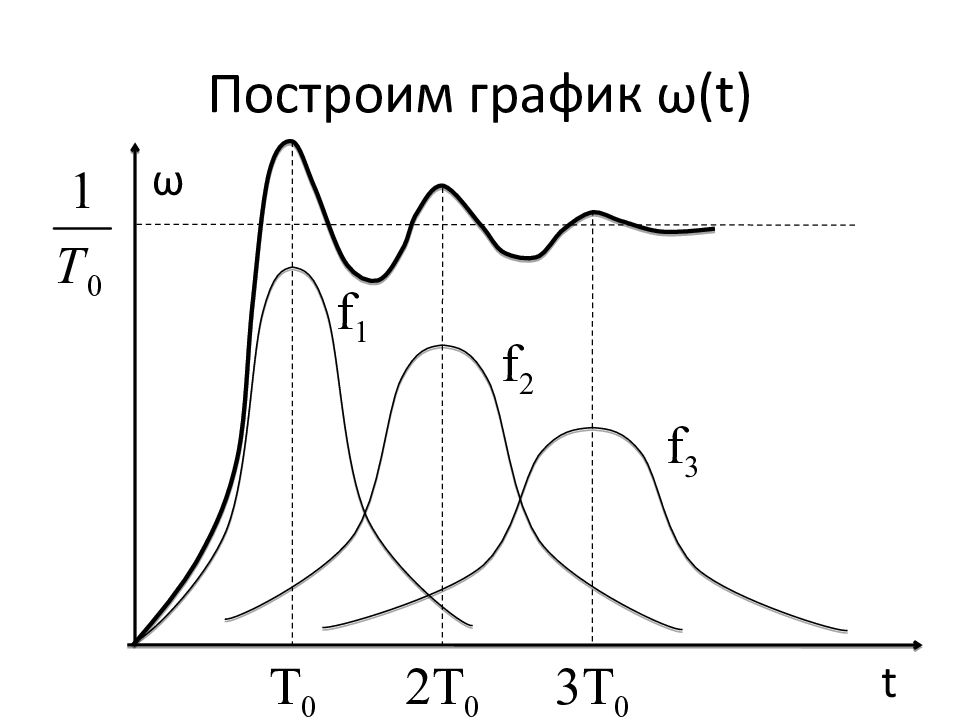
Слайд 181: Свойство графика ω (t)
График ω (t) имеет максимумы в точках t = k Т 0. Кривая ω (t) стабилизируется с течением времени и с ростом k на уровне 1/Т 0, т.е. процесс возникновения отказов становится стационарным, его локальные характеристики перестают зависеть от времени.
Слайд 182: Свойства потоков отказов
Потоки отказов могут обладать свойствами: Свойство ординарности. Вероятность совмещение 2-х и более отказов в один момент времени равна нулю. Свойство отсутствия последействия. Числа отказов для любых неперекрывающихся интервалов времени независимы. Свойство стационарности. Вероятность появления k отказов на любом промежутке времени зависит только от числа k и от длительности Δ t и не зависит от начала отсчёта времени.
Слайд 183: Виды потоков отказов
Если выполняется (1), то поток ординарный. Если выполняются (1) и (2), то поток пуассоновский. Если выполняются (1), (2), (3), то поток простейший.
Слайд 184: Для простейшего потока:
f 1 ( t ) = λ exp(– λ t ) f 2 ( t ) = λ 2 exp(– λ t ) … ω( t ) = λ T 0 = 1/ λ
Слайд 185: Для простейшего потока:
Вероятность k отказов за время t : Вероятность безотказной работы за время t : P 0 ( t ) = exp(– λ t )
Слайд 186: 3. 3. Объекты с конечным временем восстановления
Время восстановления τ = t п + t р t п – поиск неисправности; t р – ремонт или замена. Пусть объект, проработав время T 1, выходит из строя и восстанавливается в течение τ 1. Восстановленный объект через T 2 вновь отказывает, за τ 2 снова восстанавливается и т.д.
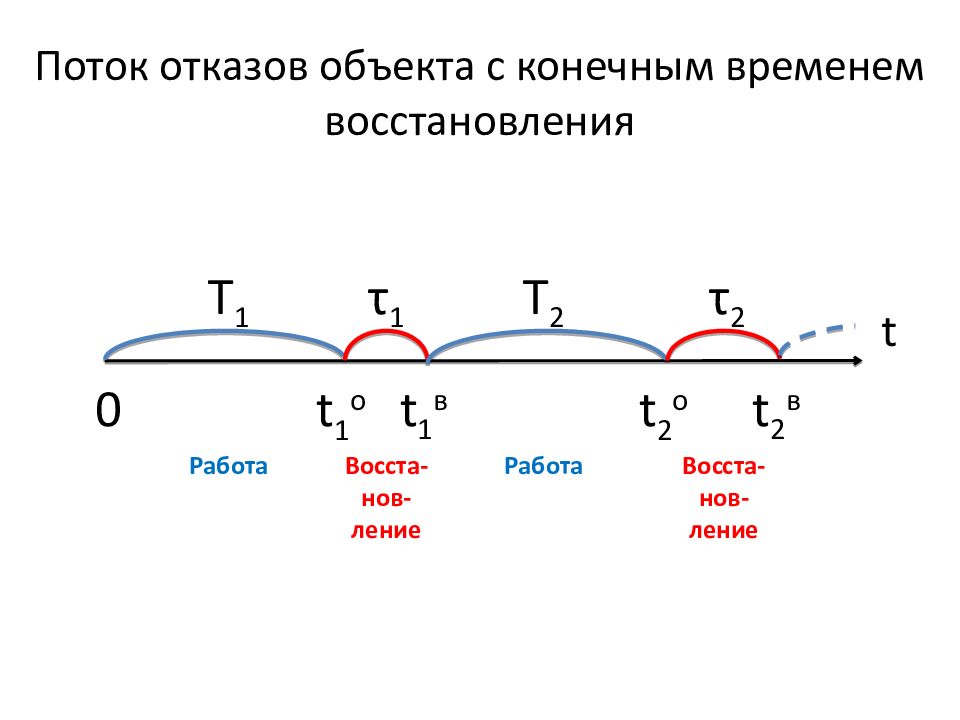
Слайд 187: Поток отказов объекта с конечным временем восстановления
t Т 1 τ 1 Т 2 τ 2 t 1 о 0 t 1 в t 2 о t 2 в Работа Восста-нов-ление Работа Восста-нов-ление
Слайд 188: Сделаем допущения:
1) Т k, τ k – независимые НСВ. 2) Все периоды работы Т k имеют: - законы F(t), f(t) ; - среднюю наработку на отказ Т = М(Т k ); - интенсивность отказов λ = 1/Т. 3) Все периоды восстановления τ k имеют: - законы G(t), g(t) ; - среднее время восстановления τ = М( τ k ) ; - интенсивность восстановлений μ = 1/ τ. 4) Поток отказов и восстановлений – простейший.
Слайд 189: Введём понятие коэффициента готовности Кг( t)
Кг( t) – это вероятность того, что в момент времени t объект находится в работоспособном состоянии (РСС). Найдём зависимость Кг( t). Вероятность застать объект в РСС в момент ( t + Δ t ) зависит от его состояния в момент t и его поведения на интервале Δ t.
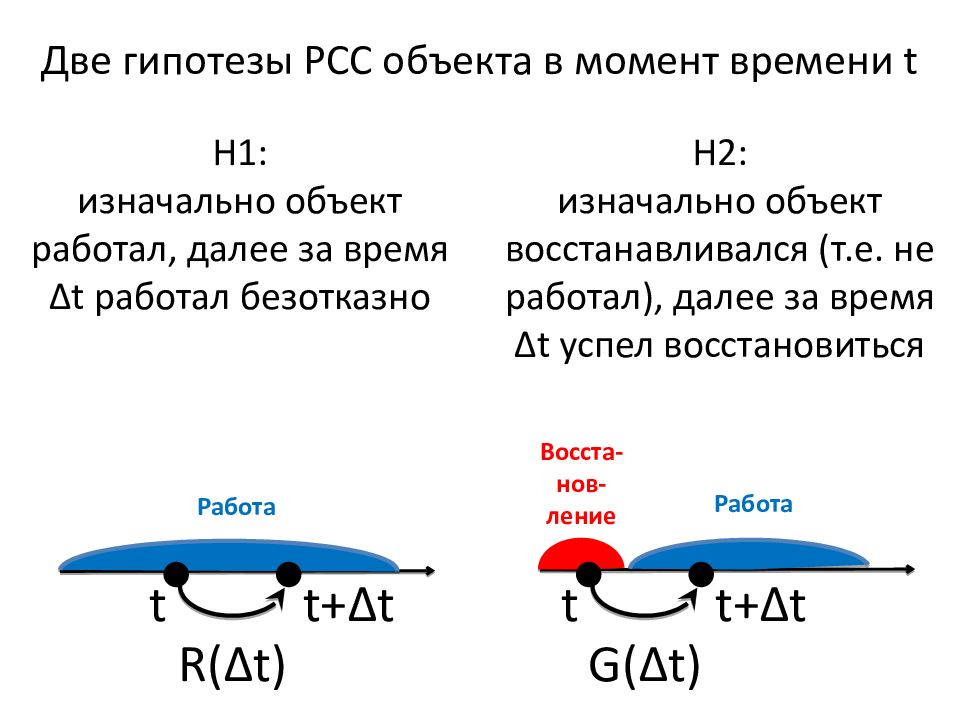
Слайд 190: Две гипотезы РСС объекта в момент времени t
t Работа Работа Восста-нов-ление t+ Δ t t t+ Δ t Н1: изначально объект работал, далее за время Δ t работал безотказно Н2: изначально объект восстанавливался (т.е. не работал), далее за время Δ t успел восстановиться R( Δ t) G( Δ t)
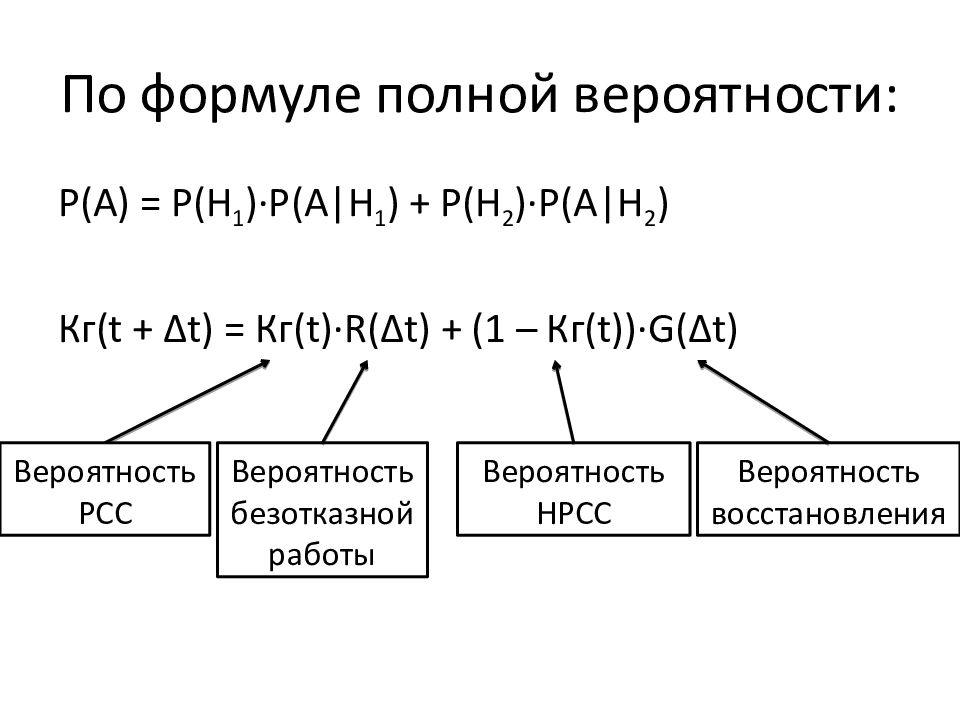
Слайд 191: По формуле полной вероятности:
Р(А) = Р(Н 1 )∙Р(А | Н 1 ) + Р(Н 2 )∙Р(А | Н 2 ) Кг( t + Δ t ) = Кг( t )∙ R( Δ t ) + (1 – Кг( t ) ) ∙ G( Δ t ) Вероятность РСС Вероятность безотказной работы Вероятность НРСС Вероятность восстановления
Слайд 192
В разделе 3.1 доказано, что: R( Δ t ) = 1 – λΔ t; G( Δ t ) = μΔ t. Подставим:
Слайд 194
Коэффициент неготовности – вероятность нахождения объекта в НРСС. Кнг = 1 – Кг Кнг (0) = 0 Кнг ( ∞) = λ /( λ + μ ) = τ /(Т+ τ ) график Кнг ( t) Коэффициент аварийного простоя – относительная длительность восстановления. q ав = λ / μ = τ /Т
Слайд 195: Глава 4. Вероятностные модели для расчёта надёжности 4.1. Общие положения
Система состоит из множества элементов. Надёжность системы зависит от надёжности её элементов и от её конфигурации. Каждый элемент системы и сама система могут находиться только в двух состояниях – работы или отказа. Если все элементы системы работают, то и сама система тоже работает. Если все элементы отказали, то и система отказала.
Слайд 196: Введем обозначения
А i – событие безотказной работы i -го элемента; А i – событие отказа i -го элемента; А с – событие безотказной работы системы; А с – событие отказа системы;
Слайд 197: Системы отображаются в виде:
физических схем: они имеют действительные, электрические связи; логических (расчётных) схем: они отражают логические связи, в смысле надёжности. Отказом системы считают отсутствие связи между началом и концом логической схемы.
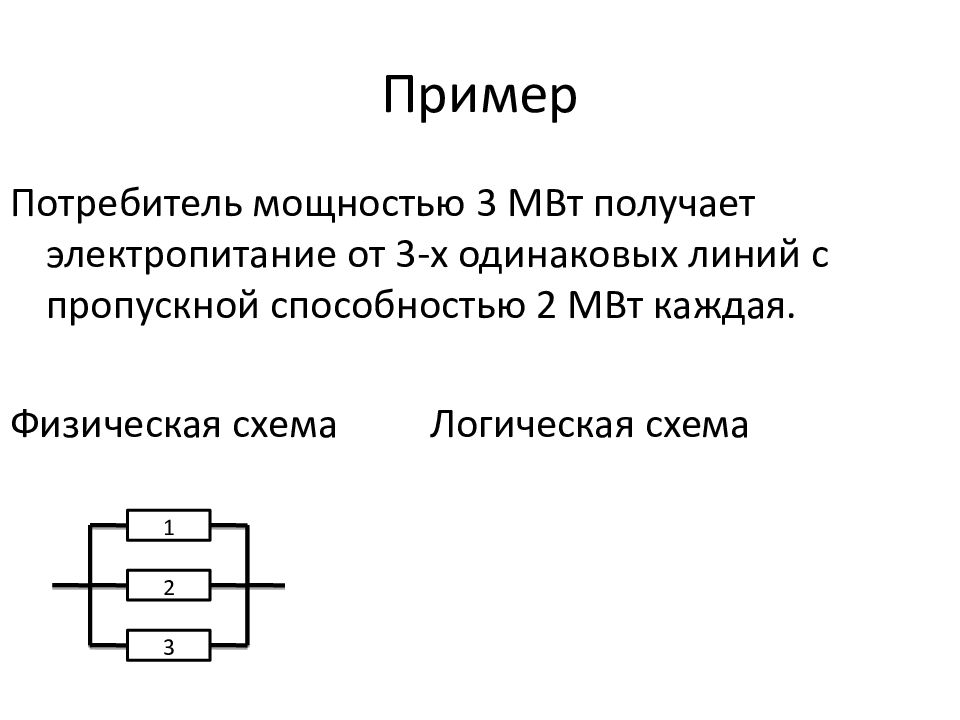
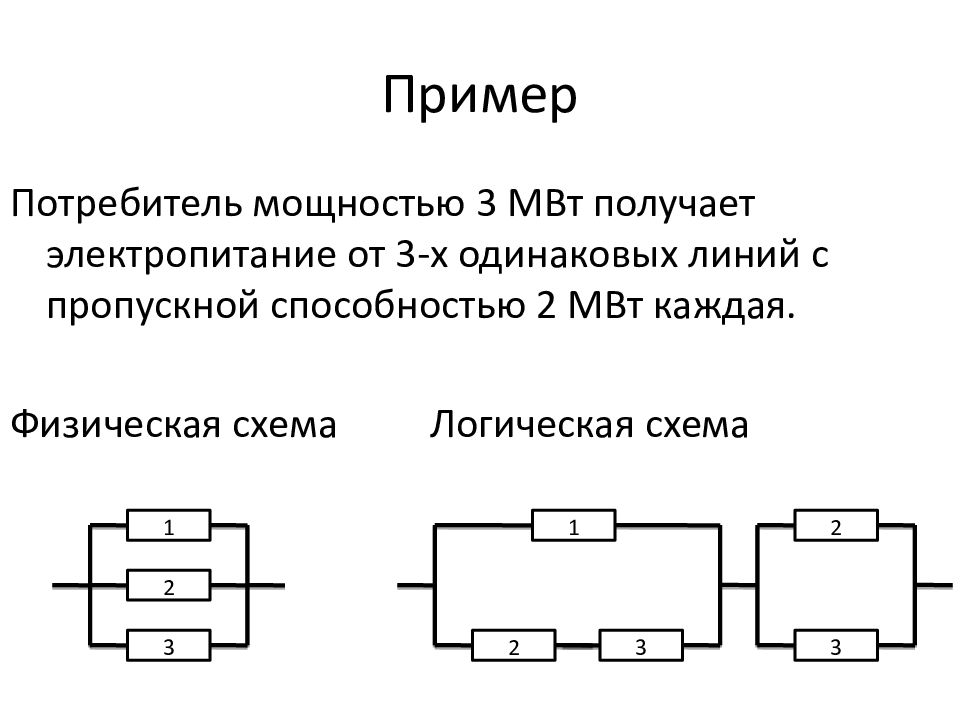
Слайд 198: Пример
Потребитель мощностью 3 МВт получает электропитание от 3-х одинаковых линий с пропускной способностью 2 МВт каждая. Физическая схема Логическая схема 1 2 3
Слайд 199: Пример
Потребитель мощностью 3 МВт получает электропитание от 3-х одинаковых линий с пропускной способностью 2 МВт каждая. Физическая схема Логическая схема 1 2 3 1 2 3 2 3
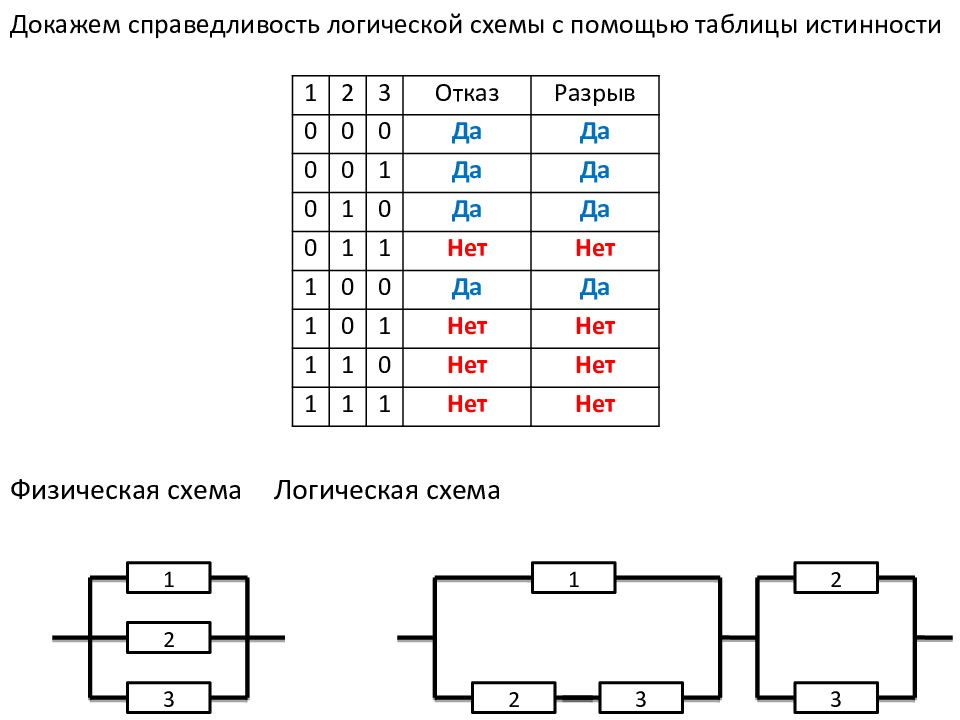
Слайд 200
Докажем справедливость логической схемы с помощью таблицы истинности Физическая схема Логическая схема 1 2 3 1 2 3 2 3 1 2 3 Отказ Разрыв 0 0 0 Да Да 0 0 1 Да Да 0 1 0 Да Да 0 1 1 Нет Нет 1 0 0 Да Да 1 0 1 Нет Нет 1 1 0 Нет Нет 1 1 1 Нет Нет
Слайд 201: 4.2. Последовательное соединение элементов
Последовательным (в смысле надёжности) называют такое соединение, при котором отказ одного элемента приводит к отказу всей системы, но не изменяет надёжности других элементов. Тогда вероятность безотказной работы системы равна системы равна произведению б.о.р. всех элементов: Р(А с ) = Р(А 1 ) ∙ Р(А 2 ) ∙ … ∙ Р(А n )
Слайд 202: 4.2.1. При отсутствии восстановления элементов
Вероятность б.о.р. системы, состоящей из независимых и невосстанавливаемых элементов в течение времени t : R с ( t) = R 1 ( t) ∙ R 2 ( t) ∙ … ∙ R n ( t) Т.к. R i (t) = exp(– λ i t), то R с ( t) = exp(– λ 1 t) ∙ exp(– λ 2 t) ∙ … ∙ exp(– λ n t ) = = exp(– ( λ 1 + λ 2 + … + λ n ) t)
Слайд 203
С другой стороны R с ( t) = exp(– λ с t) Значит λ с = λ 1 + λ 2 + … + λ n 1/Т с = 1/Т 1 + 1/Т 2 + … + 1/Т n ; Т с = 1 / ( 1/Т 1 + 1/Т 2 + … + 1/Т n )
Слайд 204: 4.2.2. При мгновенном восстановлении элементов
Число отказов системы равно сумме чисел отказов элементов. Допустим, за время t : элемент 1 претерпевает h 1 отказов; элемент 2 претерпевает h 2 отказов; … элемент n претерпевает h n отказов. Рассмотрим поток отказов системы:
Слайд 205
––––x––––––––––x–––––––x––––––––––––––– 1 эл. ––––––––x–––––––––––––––x–––––––––––––– 2 эл. –––––x–––––––––––––––––––––––––––x––––– 3 эл. ––––––––––x–––––––––––––––––––––x–––––– 4 эл. –––– хх –– х –x–––– х –––––––– хх –––––––x х ––––– Система h с = h 1 + h 2 + … + h n = > λ с = λ 1 + λ 2 + … + λ n
Слайд 206: Вероятность появления k отказов на интервале Δ t :
Вероятность б.о.р. системы: R(t) = exp(– λ с t) = exp(– t /Т с )
Слайд 207: 4.2.3. При конечном времени восстановления
В этом случае при отказе элемента, на время его восстановления отключается вся система. После окончания восстановления элемента все элементы начинаю т работать так, как если бы восстановление происходило мгновенно.
Слайд 208
Дано: последовательность средних периодов б.о.р. элементов: Т 1, Т 2, …; со средним временем б.о.р. системы: Т с = 1 / ( 1/Т 1 + 1/Т 2 + … ) и последовательность средних периодов восстановления элементов: τ 1, τ 2, … Найти среднюю длительность восстановления системы τ с
Слайд 209: Решение
Вероятность отказа i -го элемента на отрезке Δ t: λ i Δ t Вероятность отказа системы на отрезке Δ t: λ с Δ t Тогда условная вероятность отказа i -го элемента при условии, что на этом же интервале отказала система, равна: λ i Δ t / λ с Δ t = λ i / λ с По формуле полной вероятности найдём распределение длительности восстановления для системы, начавшегося в момент t : G c (t) =
Слайд 215: 4.3. Параллельное соединение элементов
4.3.1. Резервирование одного элемента (n-1) резервным Система с параллельным ( в смысле надёжности) соединением элементов выходит из строя только в случае отказа всех её элементов.
Слайд 216
Вероятность отказа такой системы равна: Р(А с ) = Р(А 1 ) ∙ Р(А 2 ) ∙ … ∙ Р(А n ) (при этом считаем, что отказы всех элементов независимы). Вероятность б.о.р. системы равна: Р(А с ) = 1 – (1 – Р(А 1 )) ∙ (1 – Р(А 2 )) ∙ … ∙ (1 – Р(А n )) Вероятность отказа системы: Q с ( t) = Q 1 ( t) ∙ Q 2 ( t) ∙ … ∙ Q n ( t) Вероятность б.о.р. системы равна: R c ( t ) = 1 – (1 – R 1 ( t )) ∙ (1 – R 2 ( t )) ∙ … ∙ (1 – R n ( t ))
Слайд 217
При равнонадежных элементах и экспоненциаль-ном законе: Q с ( t) = (1 – exp(– λ t)) n, где λ – частота отказа элемента схемы. Вычислим среднее время б.о.р. системы: Т с = …
Слайд 218
При n → ∞ Т с = ln ( n )/ λ Например: n = 100: Т с = 4,6/ λ n = 1 0 00: Т с = 6,9/ λ n = 1 0 0 00: Т с = 9,2/ λ Вычислим параметры системы Т с, τ с, λ с, μ с через параметры равнонадёжных элементов Т, τ, λ, μ : Вывод формул выполним через величины: q с, q – вероятности застать систему и элемент в состоянии простоя.
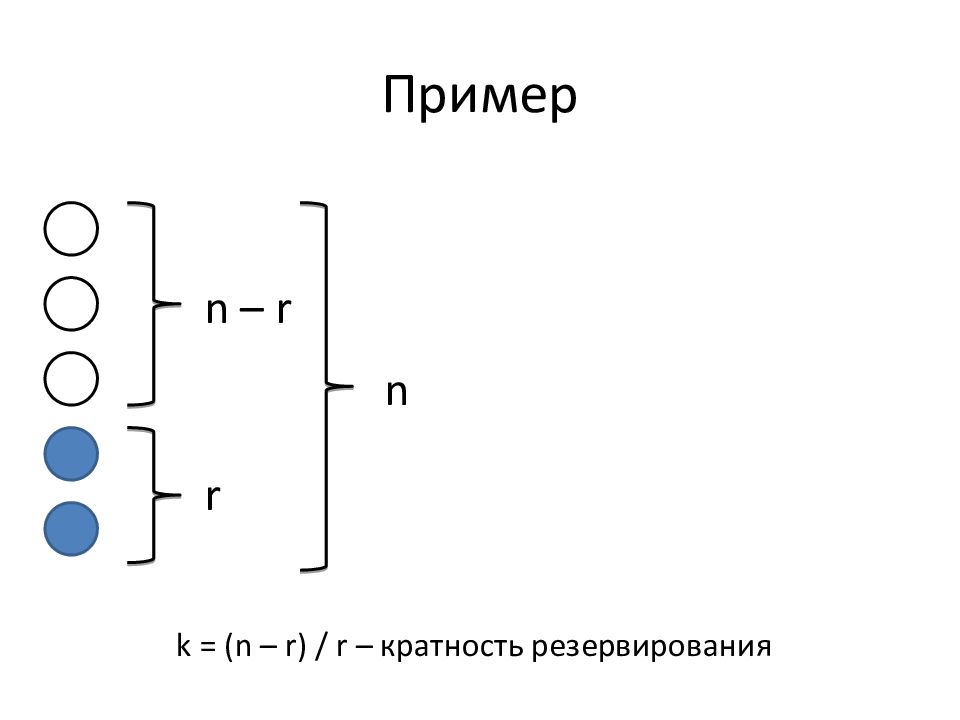
Слайд 220: 4.3.2. Резервирование r рабочих элементов ( n – r ) резервными
Пусть система состоит из n элементов. Пусть для нормального функционирования системы необходимо r элементов. Тогда остальные ( n – r ) элементов являются резервными. Отказ системы наступает при выходе из строя ( n – r + 1) элементов.
Слайд 222
Как рассчитать функции надежности Rc и отказа Q с всей системы, зная Ri и Qi каждого элемента? В общем виде – громоздкое выражение, поэтому примем допущение, что все элементы равнонадёжны и имеют функции R 1 = R 2 = … = R, Q 1 = Q 2 = … = Q. Сначала выведем формулы для частного случая.
Слайд 224: Решение
Очевидно, что для системы: Rc + Qc = 1 и для каждого элемента: R + Q = 1 Отсюда следует, что: Rc + Qc = (R + Q) 5 =
Слайд 226: Виды резервирования
По способу включения резервных элементов резервирование бывает: постоянное (резервные объекты включены в систему в течение всего времени работы и находятся в одинаковых с другими объектами условиях) замещением (резервные объекты включают в систему вместо основных после отказа последних)
Слайд 227: Постоянное резервирование (неявное)
Отказавший элемент должен отключаться защитной аппаратурой, надёжность которой будет определять надёжность всей схемы.
Слайд 228: Резервирование замещением (явное)
Отказавший элемент должен отключаться защитной аппаратурой, а резервный элемент должен включаться аппаратурой автоматики. Надёжность этих видов аппаратуры будет определять надёжность всей схемы.
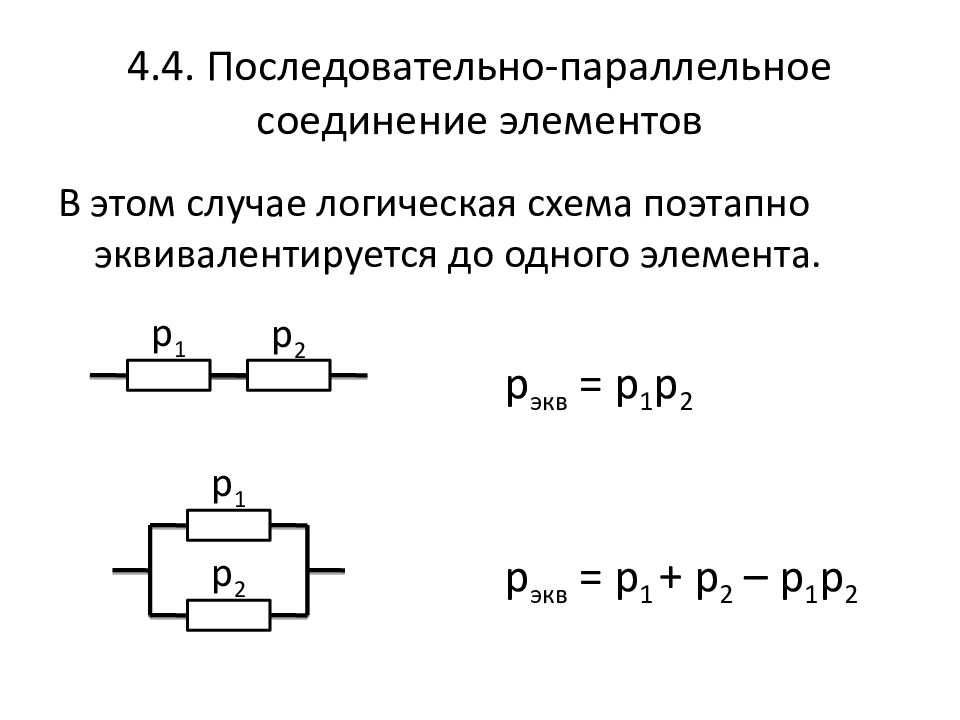
Слайд 229: 4.4. Последовательно-параллельное соединение элементов
В этом случае логическая схема поэтапно эквивалентируется до одного элемента. р 1 р 2 р 1 р 2 р экв = р 1 р 2 р экв = р 1 + р 2 – р 1 р 2
Слайд 230: Можно доказать, что:
при последовательном соединении р общ меньше меньшего; при параллельном соединении р общ больше большего, но меньше 1.
Слайд 231: 4.5. Метод минимальных путей и сечений
Этот метод применяют, когда структуру системы нельзя свести к последовательно-параллельным цепочкам. Введем следующие понятия: Путь – последовательность смежных элементов, соединяющая вход и выход схемы. Сечение – совокупность элементов, удаление которых приводит к нарушению связи между входом выходом.
Слайд 232
Минимальный путь – путь, удаление из которого хотя бы одного элемента приводит к тому, что оставшееся множество элементов не будет путём. Минимальное сечение – сечение, удаление из которого хотя бы одного элемента приводит к тому, что оставшееся множество элементов перестаёт быть сечением.
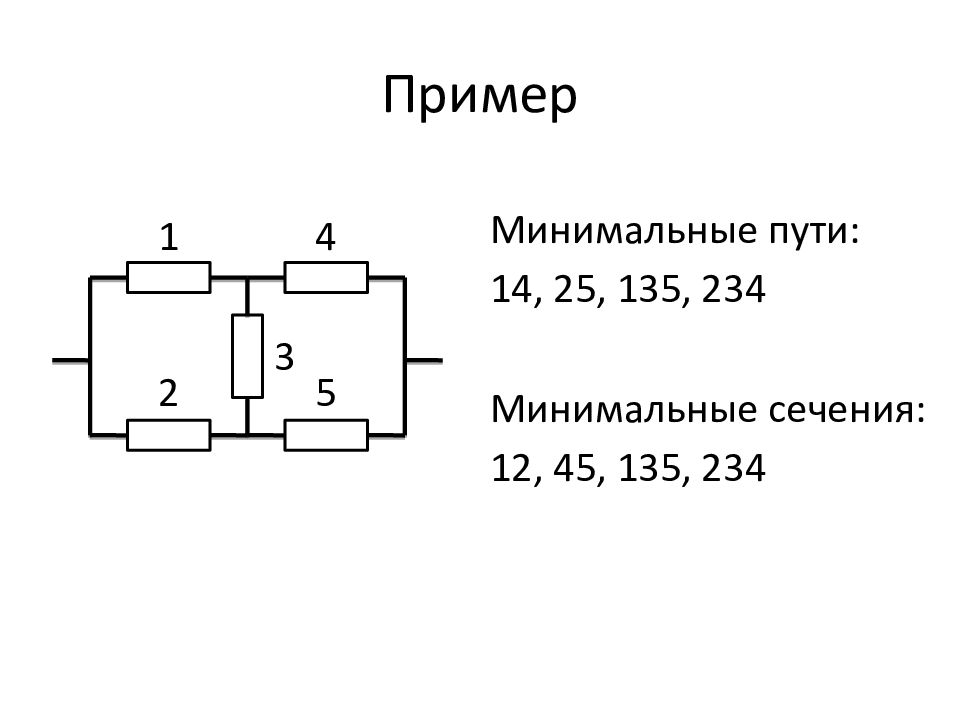
Слайд 233: Пример
Минимальные пути: 14, 25, 135, 234 Минимальные сечения: 12, 45, 135, 234 1 2 4 5 3
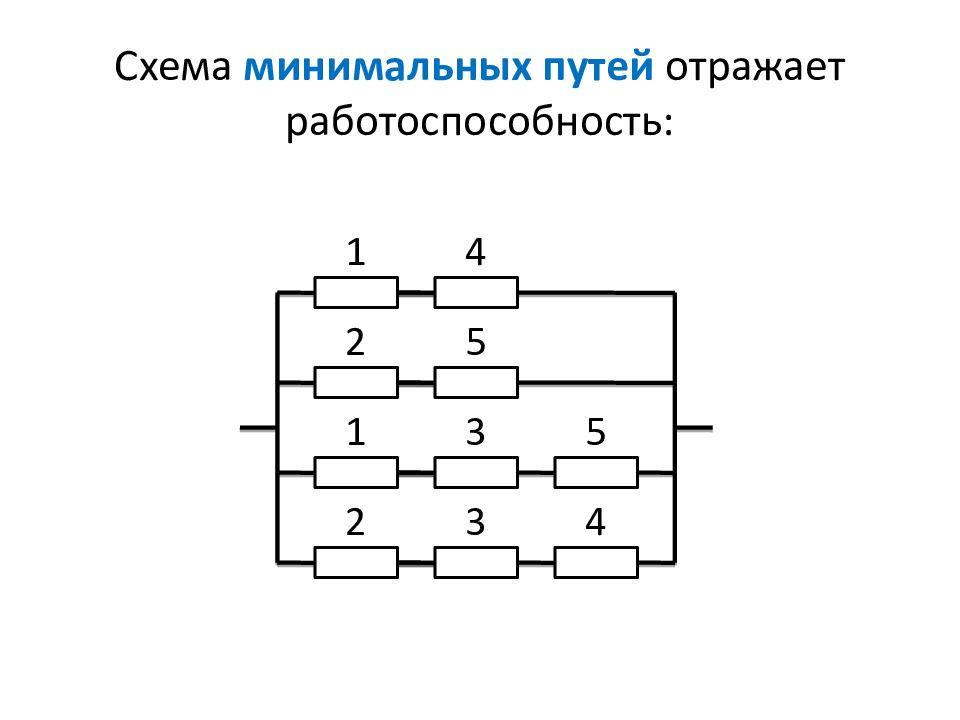
Слайд 234: Схема минимальных путей отражает работоспособность:
1 4 2 5 1 3 2 3 5 4
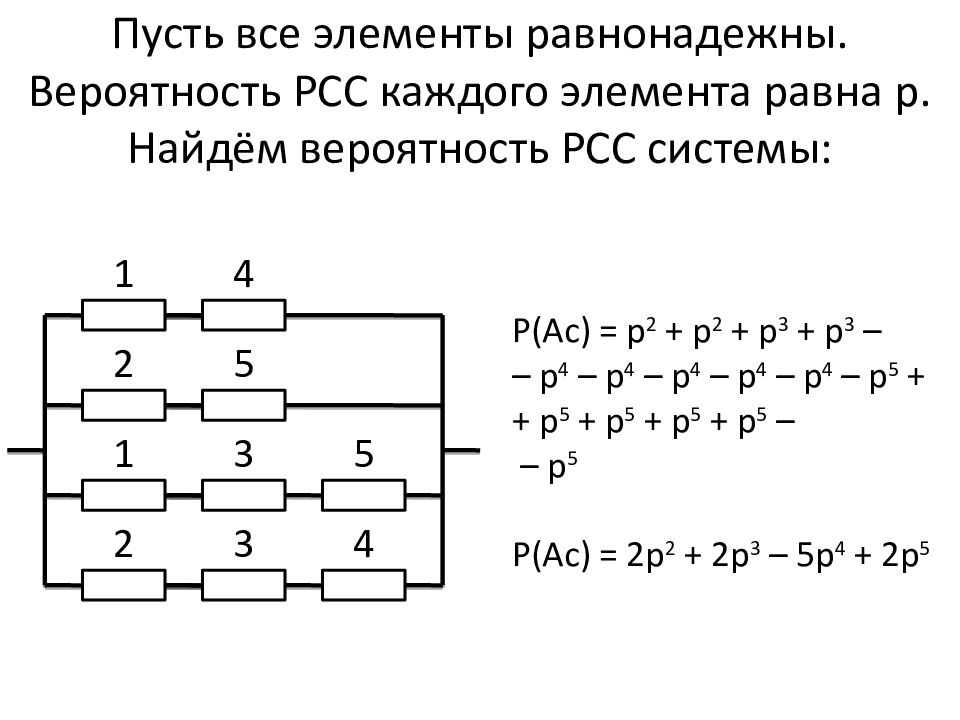
Последний слайд презентации: Теория надежности в электроэнергетике: Пусть все элементы равнонадежны. Вероятность РСС каждого элемента равна р. Найдём вероятность РСС системы:
1 4 2 5 1 3 2 3 5 4 Р(Ас) = р 2 + р 2 + р 3 + р 3 – – р 4 – р 4 – р 4 – р 4 – р 4 – р 5 + + р 5 + р 5 + р 5 + р 5 – – р 5 Р(Ас) = 2р 2 + 2р 3 – 5р 4 + 2р 5