O’ZBEKSTAN RESPUBLIKASI JOQARI HA’M ORTA ARNAWLI BILIMLENDIRIW — презентация

O’ZBEKSTAN RESPUBLIKASI JOQARI HA’M ORTA ARNAWLI BILIMLENDIRIW MINISTIRLIGI BERDAQ ATINDAG’I QARAQALPAQ MA’MLEKETLIK UNIVERSITETI Matematika fakulteti Matematika ta’lim bag’darı 1- kurs studenti Rametullaev Muratbekdin ' Analitik geometriya pa’ninen Tema : Tegislik ten'lemeleri teması boyınsha KURS JUMISI prezintatsiyasi Orinladi : Raxmetullaev. M Qabilladi : Seydullaev.A

Изображение слайда

Tegislik hám tuwri sızıqtıń vektor hám koordinat formasındaǵı teńlemeleri Tuwri sızıqlardıń o'zara jaǵdayı Tuwri sızıq menen tegisliktiń ozaro jaǵdayları Eki tegisliktiń o'zara jaǵdayı Tuwri sızıqlar hám tegisliklerdiń perpendikulyarlıǵı Úsh perpendikulyar haqqındaǵı teorema

Изображение слайда

(1) F  x, y, z   0 teńlik x, y, z lardıń tek ayırım mánislerinde ǵana orınlı bolsa, onda (1) di x  x 0, y  y 0, z  z 0 x, y, z larǵa qarata teńleme dep ataymız. Úsh san (1) teńlemeni qanaatlandıradı deymiz, eger (1) degi belgisizler ornına usı sanlardı qoyǵanda teńlik teńlikke aylansa. (1) teńlemeni qanaatlandırıwshı hár bir x 0, y 0, z 0 sanlar úshligine keńislik M ( x 0, y 0, z 0 ) n oqatın sáykes qoyamız. Bunday noqatlardıń geometriyalıq ornın bet dep ataymız, al (1) di sol bettiń teńlemesi dep ataymız. Eger bet teńlemesi berilgen bolıp, qanday da bir noqattıń sol bette jatıw yamasa jatpawın tekseriw talap etilgen bolsa, onda berilgen noqattıń teńlemeniń belgisizleri ornina qoyiw jetkilikli. Analitikalıq wazıypası qaralıp atırǵan betti onıń teńlemesi járdeminde koordinataların geometriyanıń úyreniw.

Изображение слайда

Bettiń ıqtıyarlı M  x, y, z  noqatı onıń jıljıwshı noqatı dep ataladı Mısal retinde sferanıń teńlemesin dúzeyik. Sferanıń anıqlaması boyınsha, sferanıń orayı dep atalatuǵın C  a, b, c  noqattan sferanıń jıljıwshı noqatı arasındaǵı aralıq r turaqlı. Demek,  x  a  2   y  b  2   z  c  2  r Yamasa  x  a  2   y  b  2   z  c  2  r 2 Eger sferanıń orayı koordinatalar basında bolsa, onda x 2  y 2  z 2  r 2 Keńisliktegi analitikalıq geometriyada tiykarınan algebralıq teńlemeler menen anlatılgan betler úyreniledi. Máselen, teńlemesi (2) Ax  B y  C z  D  0 kórinisindegi bet 1-tártipli bet dep ataladı. Teńlemesi Ax 2  B y 2  C z 2  2 D x y  2 E x z  2 F y z  2 G x  2 H y  2 K z  L  0 (3)

Изображение слайда

II. 1-teorema. Dekart koordinatalar sistemasında tegislik 1-tártipli bet bolip tabıladı. . Ísbat. Qanday da bir dekart koordinatalar sistemasında berilgen  tegisliginde onıń qanday da bir noqatı M 0 ( x 0, y 0, z 0 ) hám oǵan perpendikulyar ótken qanday da bir n  { A, B, C } vektor berilgen bolsın. Aytayıq, M ( x, y, z ) tegisliktiń jıljıwshı noqatı bolsın. → Bul noqat  tegisliginde jatıwı ushın M 0 M vektor n ge perpendikulyar bolıwı shárt, yaǵnıy n  M 0 M. 0 Vektorlardıń perpendikulyarlıq shártinen M M ∘ n →  0 yamasa A  x  x 0   B  y  y 0   C  z  z 0   0 (4) kelip shıǵadı. Eger M ( x, y, z ) noqat  tegisliginde jatpasa, (4) " orınlı bolmaydı.",

Изображение слайда

Ax  B y  C z  D  0 payda boladı. Teorema dálillendi. Tegislikke perpendikulyar bolgan nolge teń bolmagan hár qanday vektorli tegisliktiń normal vektori dep ataladi. Sol sebepli, (4) tenleme normal vektori n bolgan hám M 0 ( x 0, y 0, z 0 ) noqattan ótken tegislik tenlemesin anlatadi. 2-teorema. Dekart koordinatalar sistemasında qálegen 1-tártipli tenleme tegislikti anıqlaydı. Dáliyli. Qanday da bir dekart koordinatalar sistemasında (2) teńleme berilgen bolsın. Aytayıq, x 0, y 0, z 0 lar usı teńlemeniń bazı bir sheshimi bolsın, yaǵnıy (2) ti qanaatlandırıwshı sanlar bolsın. Onda

Изображение слайда

Ax 0  B y 0  C z 0  D  0 (6) boladı. (2) den (6) nı alsaq. A  x  x 0   B  y  y 0   C  z  z 0   0 payda boladı. Bul tenlemenin normal vektori ekenligi belgili. n boli p, M 0 ( x 0, y 0, z 0 ) noqatınan ótken tegislik teńlemesi. (4) teńleme (2) ge ekvivalent bolģanı ushın (2) de a tegisliktiń teńlemesi boladı. Teorema dálillendi. Tegisliktiń (2) tenlemesin onıń ulıwma teńlemesi dep ataymız. Mısal. n  {2, 2, 3} vektorga perpendikulyar bolip, M 0  1,1,1  noqattan ótken tegislik teńlemesin dúziń. Sheshiliwi. (4) tiykarında 2  x  1   2  y  1   3  z  1   0 Yamasa 2 x  2 y  3 z  7  0

Изображение слайда

teńlemeler bir tegislikti anlatsa, onda bul teńlemelerdiń sáykes koefficientleri óz ara proporcional boladı.. 1 1 1 Daliyl. Haqıyqatında da, eger teorema shárti orınlı bolsa, onda n 1 →  { A, B, C }, 2 2 2 → n 2  { A, B, C } vektorlar berilgen tegislikke perpendikulyar boladı, demek., A 2, B 2, C 2 olar óz-ara kolleniar. Vektorlardıń kolleniarlıq shárti boyınsha, s a nlar A 1, B 1, C 1 sanlarga proporcional boladı. Eger proporcionallıq koefficientin  d e s e k, A 2  A 1 , B 2  B 1 , C 2  C 1 . Eger M 0 ( x 0, y 0, z 0 ) tegisliktiń qálegen noqatı bolsa, onda oniń koordinataları hárbir teńlemeni qanaatlandıradı, yaǵnıy. A 1 x 0  B 1 y 0  C 1 z 0  D 1  0 v a A 2 x 0  B 2 y 0  C 2 z 0  D 2  0 bolad ı. Eger o lar dıń Birewin  ǵa kóbeytip, ekinshisinen ayırsaq D 2  D 1   0 payda boladı. Bunnan bolsa, A 1 B 1 C 1 D 1 A 2  B 2  C 2  D 2   keli p shıǵadı.

Изображение слайда

1 ) D= 0; tengl e m e Ax  B y  C z  0 kóriniske keledi. Bul teńlemeni x= 0, y= 0, z= 0 sanlar qanaatlandıradı, yaǵnıy tegislik koordinatalar basınan ótedi. 2) C= 0; tengl e m e Ax  B y  D  0 kórinisinde boladı. Bul tegisliktiń z kósherine perpendikulyar, tegislikti normal vektori n  { A, B, 0}, ózi sol oqqa parallel ótedi. 3) B= 0, C= 0; bunda Ax  D  0 ge iye bolamız. Onıń normal vektorı n  { A, 0,0} y ha`m z kósherlerine perpendikulyar, ol jagdayda tegislik O y z tegisligine parallel ótedi. Atap aytqanda, eger

Изображение слайда

tegisligi D= 0 bolsa, x= 0 payda bolıp, bul tegislik O y z koordinatalar menen ústpe-úst túsiwine isenim payda etemiz. Joqarıdaǵıday pikirlep, Ax  C z  D  0 tengl e m e y kósherine parallel tegislikti, B y  C z  D  0 tengl e m e x kósherine parallel tegislikti aniqlaytuģınına isenim etiń. qilamiz. Bulardıń dara jaǵdayı sıpatında, y= 0 tengl e m e O x z koordinatalar tegisliginiń, z= 0 es e O x y tegisliginiń teńlemesi ekenligin kóremiz. A, B, C, D koefficientlerdiń birewi de nolge teń bolmasın. Onda erkin aģzanı teńliktiń "on" tárepine ótkerip, teńlemeni - D ga bólip jiberemiz: A x  B y  C z  1 D  D  D yamasa    1 z A B C  D  D  D x y

Изображение слайда

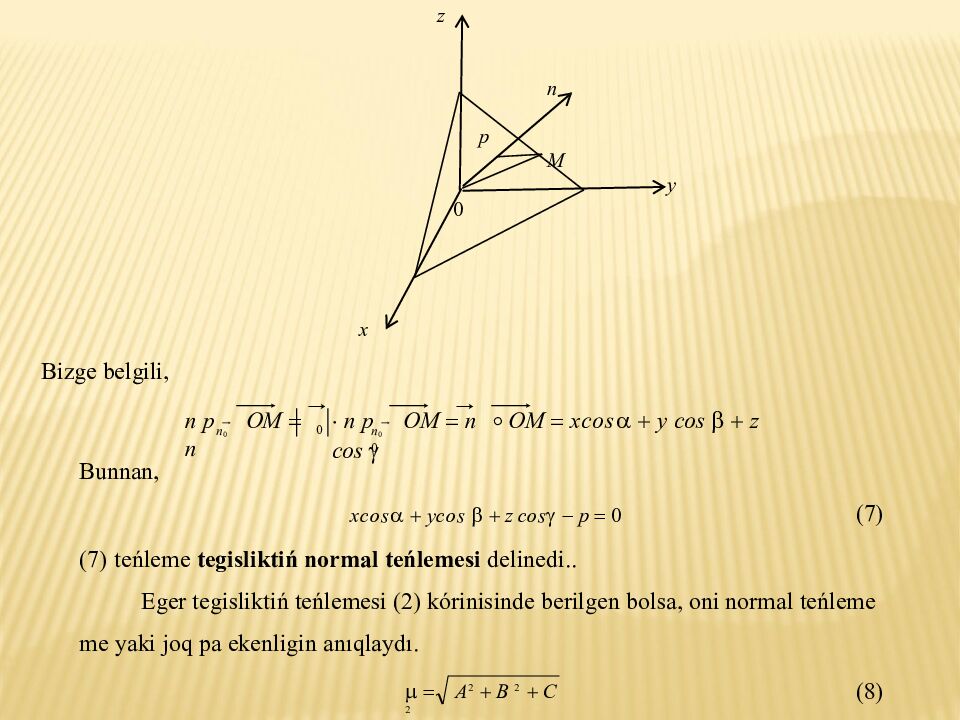
a b c x  y  z  1 (6) payda boladı. (6) teńlemeni tegisliktiń kesindilerdegi teńlemesi dep ataydı. IV. Meyli, bizge  tegisligi, onıń normalı n hám koordinatalar basınan tegislikke shekemgi aralıq p berilg e n bolsin. n vektor dıń koordinata kósherleri → menen payda etken múyeshleri , ,  bolsin. Eger n 0, n vektordıń artı bolsa, onda → n 0   cos , cos , cos   boladı. Tegisliktiń jıljıwshı noqatın M ( x, y, z ) desek, onıń radius- vektori n 0 OM   x, y, z  boladı. Sızılmadan kórinip tur, п р → OM  p

Изображение слайда

Bizge belgili, → →  п р → OM  n ∘ OM  xcos   y cos   z cos  п р → OM  n 0 n 0 0 n 0 Bun n an, (7) xcos   ycos   z cos   p  0 (7) teńleme tegisliktiń normal teńlemesi delinedi.. Eger tegisliktiń teńlemesi (2) kórinisinde berilgen bolsa, oni normal teńleme me yaki joq pa ekenligin anıqlaydı.   A 2  B 2  C 2 (8) z n p M y 0 x

Изображение слайда

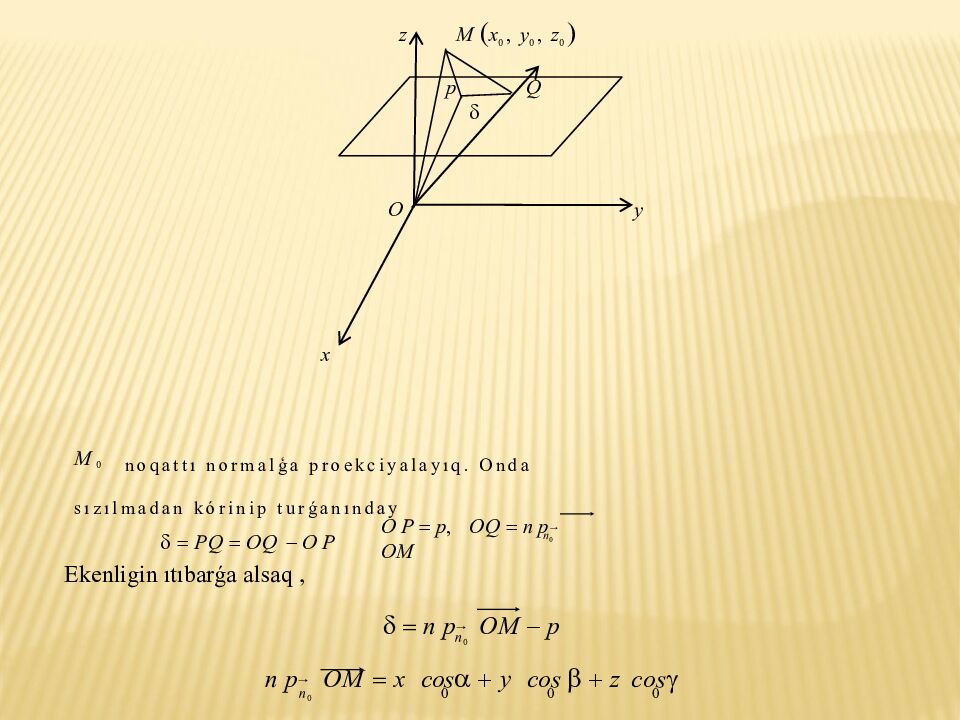
  1 bolsa, (3) normal tengl e m e ańlatpanıń mánisine qarap anıqlaymız : eger boladı, bolmasa (3) ti.   g e bólip  0 A B C D  x  y  z ∓ (9) A 2  B 2  C 2 A 2  B 2  C 2 A 2  B 2  C 2 A 2  B 2  C 2 payda etemiz. Bul teńleme normal boliwi ushin endi (9) degi belgilerden birin erkin agza D nıń belgisine keri etip alıw jetkilikli. (2) teńleme.  mánis járdeminde normal kóriniske keltirilgeni ushın 1  d ı normallawshı kóbeytiwshi de p ataladi. V. Noqattan berilgen tegislikke shekemgi aralıq. Oylayıq,  tegislik hám onda jatpaǵan qanday da bir M 0 ( x 0, y 0, z 0 ) noqat berilgen bolsın. M 0 noqatdan  t egislikke shekem d aralıqtı tabıw talap etilgen bolsın. Berilgen 0 tegisliktiń normalı n → qurıp alamız. Eger M 0 noqat hám koordinatalar bası  tegisliktiń hár qıylı táreplerinde jaylasqan bolsa, onda M 0 noqattıń  tegislikten awısıwı dep + d yamasa – d ǵa aytamiz.

Изображение слайда

n 0 O P  p, OQ  п р → OM Ekenligin ıtıbarǵa alsaq, n 0   п р → OM  p п р → OM  x cos   y cos   z cos  n 0 0 0 0 z M  x 0, y 0, z 0  p Q  O y x M 0 noqattı normalģa proekciyalayıq. Onda sızılmadan kórinip turǵanınday   PQ  OQ  O P

Изображение слайда

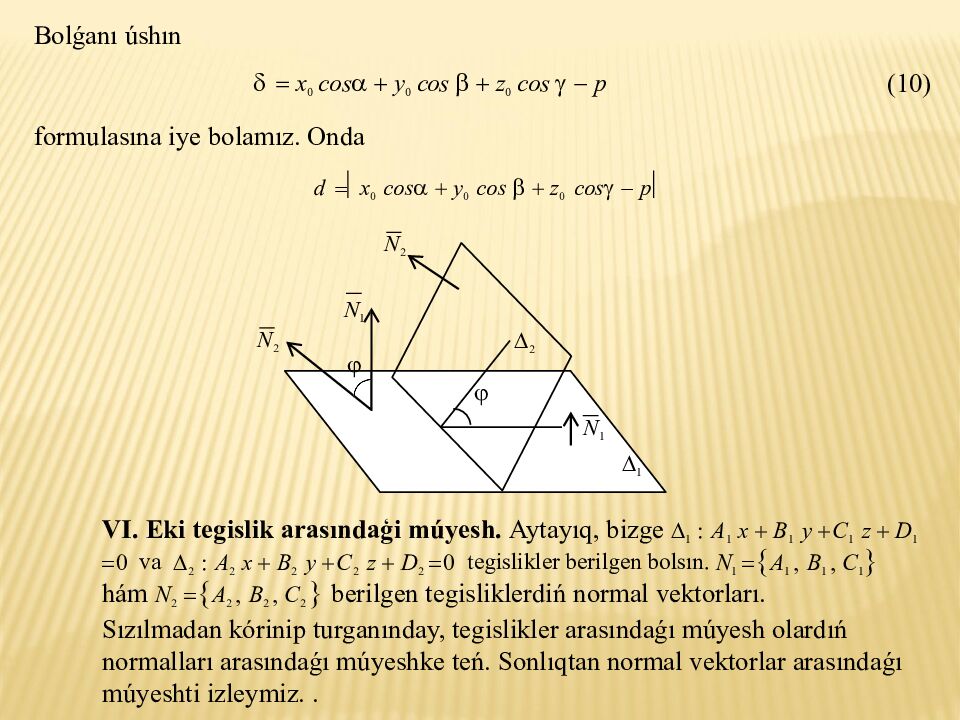
(10)   x 0 cos   y 0 cos   z 0 cos   p formulasına iye bolamız. Onda d  x 0 cos   y 0 cos   z 0 cos   p VI. Eki tegislik arasındaģi múyesh. Aytayıq, bizge  1 : A 1 x  B 1 y  C 1 z  D 1  0 va  2 : A 2 x  B 2 y  C 2 z  D 2  0 tegislikler berilgen bolsın. N 1   A 1, B 1, C 1  hám N 2   A 2, B 2, C 2  berilgen tegisliklerdiń normal vektorları. Sızılmadan kórinip turganınday, tegislikler arasındaǵı múyesh olardıń normalları arasındaǵı múyeshke teń. Sonlıqtan normal vektorlar arasındaǵı múyeshti izleymiz.. N 2 N 1 N 2  2   N 1  1

Изображение слайда

1 2 → → N ∘ N N 1  N 2 cos   Yamasa 2 1 A 2 A 2  B 2  C 2 2 2  B 2  C 2  1 1 A 1 A 2  B 1 B 2  C 1 C 2 cos   (11) 1 2 2 Eger    bolsa,    bolad ı. Onda cos   0 hám (11)g e tiykar A 1 A 2  B 1 B 2  C 1 C 2. Bul teńlikti tegisliklerdiń perpendikulyarlıq shárti dep ataydı.. N 1 vektor N 2 vektorg e Eger  1 tegislik  2 tegislikke parallel bolsa, onda kolleniar bolad ı. Vektorlar dıń kolleniarlik shártine qaray a A 1  B 1  C 1 A 2 B 2 C 2 boladı. Bul qatnas tegisliklerdiń parallellik shárti dep ataladı.

Изображение слайда

VII. Úsh noqattan ótken tegislik teńlemesi. Bizg e  te gisliktıń úsh M 1  x 1, y 1, z 1 , M 2  x 2, y 2, z 2 , M 3  x 3, y 3, z 3  noqatı berilg e n bolsın. Eger M ( x, y, z ) M 1 M, M 1 M 2, M 1 M 3  usi tegisliktiń jiljıwshı noqatı bolsa, onda vektorlar tegislikte jatadı, yagniy olar " komplanar " boladı.. M 1 M   x  x 1, y  y 1, z  z 1 , M 1 M 2   x 2  x 1, y 2  y 1, z 2  z 1 , M 1 M 3   x 3  x 1, y 3  y 1, z 3  z 1  ekenliginen hám vektorlardıń komplanarlıq shártinen z 3  z 1 z 2  z 1  0 z  z 1 y  y 1 y 2  y 1 y 3  y 1 x  x 1 x 2  x 1 x 3  x 1 kelip shıǵadı.

Изображение слайда