Первый слайд презентации: Пересечение поверхности и плоскости. Сечение поверхностей 2-го порядка
Построение линий пересечения поверхностей Способ вспомогательных секущих плоскостей 1 Лекция 5 Лектор: Стриганова Л.Ю.
Слайд 2
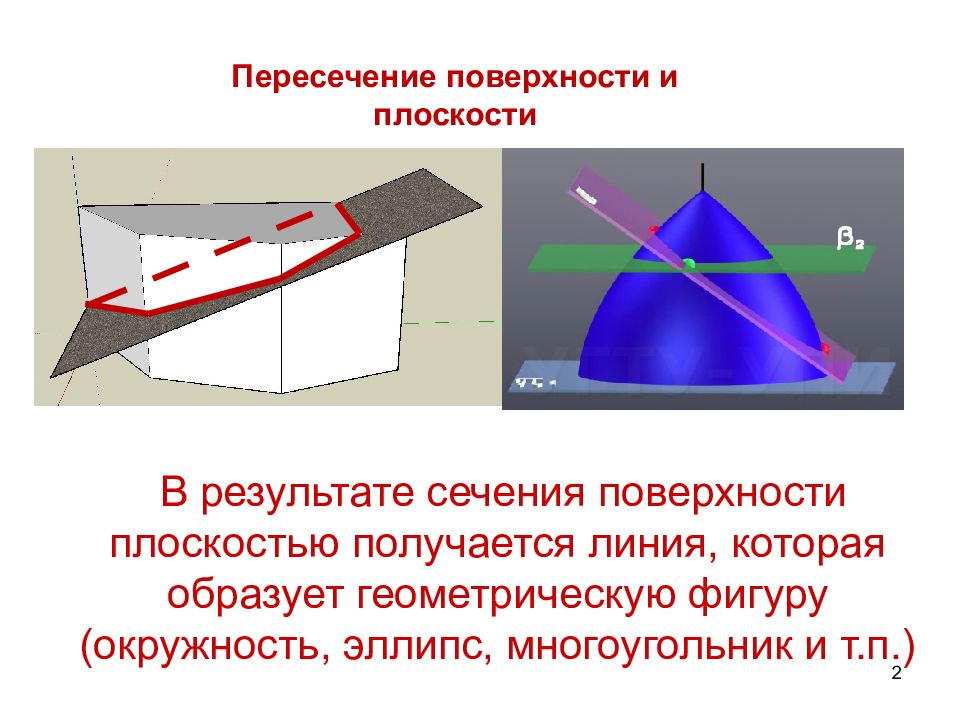
2 В результате сечения поверхности плоскостью получается линия, которая образует геометрическую фигуру (окружность, эллипс, многоугольник и т.п.) Пересечение поверхности и плоскости
Слайд 3: СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ
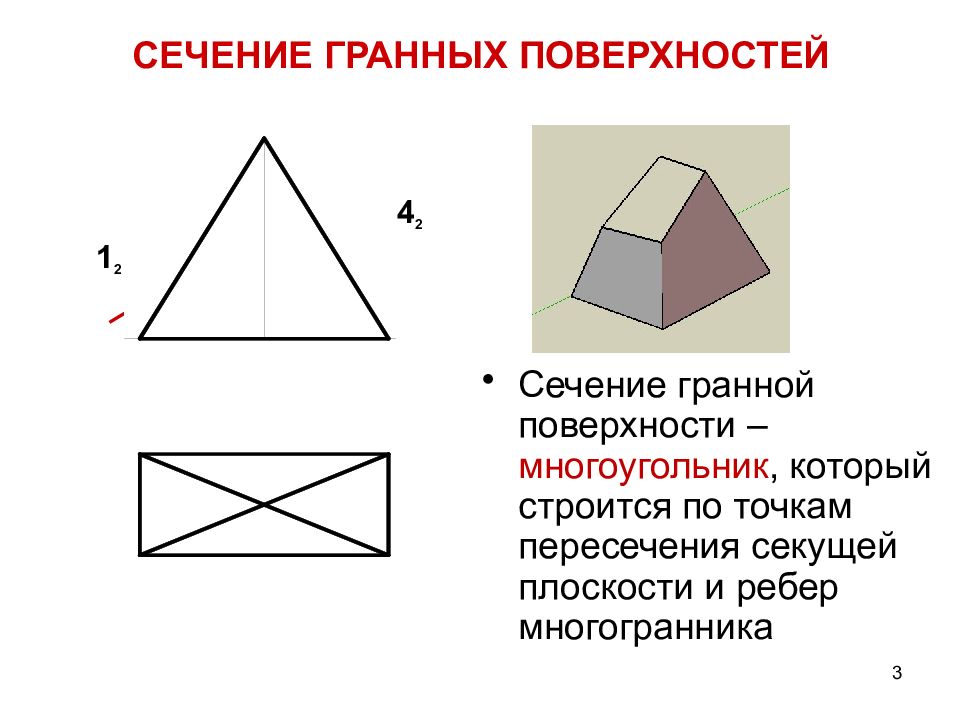
3 СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ Сечение гранной поверхности – многоугольник, который строится по точкам пересечения секущей плоскости и ребер многогранника 1 2 Ξ 2 2 3 2 Ξ 4 2 1 1 2 1 4 1 3 1
Слайд 4: СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
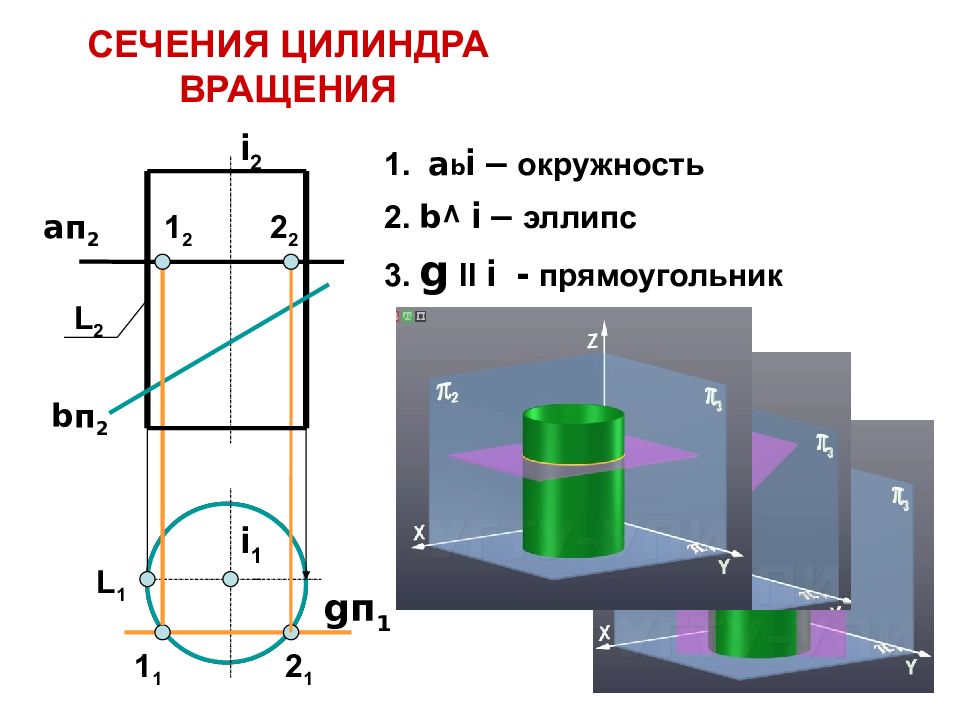
4 СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ 1. a b i – окружность 2. b ^ i – эллипс 3. g ll i - прямоугольник L 2 i 2 i 1 L 1 a п 2 b п 2 g п 1 1 1 2 1 1 2 2 2
Слайд 5: СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
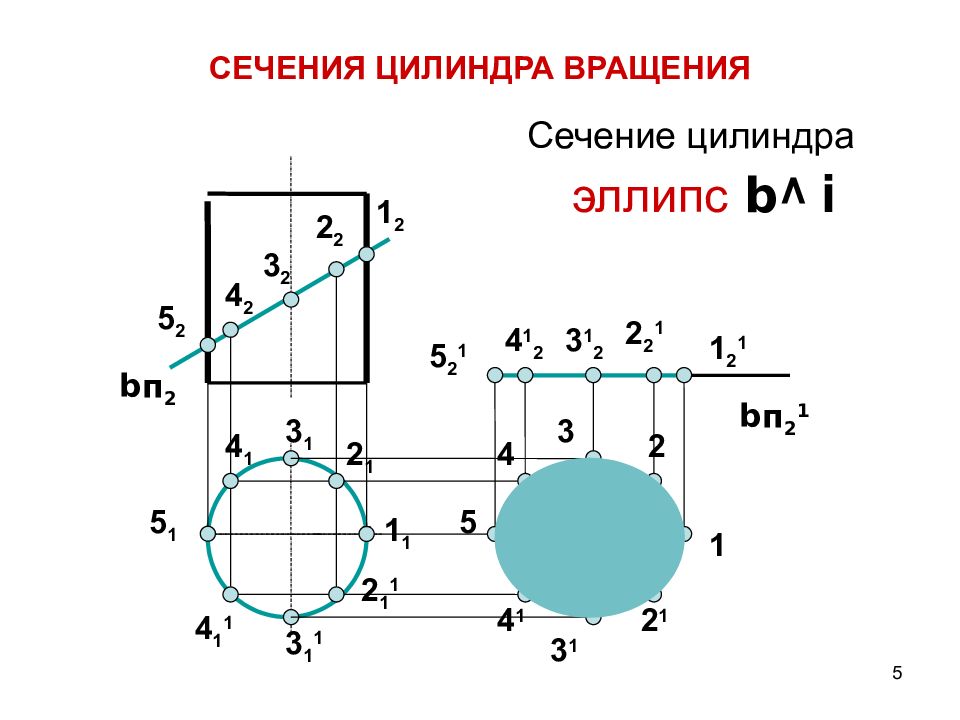
5 Сечение цилиндра эллипс b ^ i СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ b п 2 1 1 2 1 2 1 1 1 1 2 2 1 1 2 2 1 2 1 2 2 2 1 3 2 3 3 1 3 1 1 3 1 2 3 1 4 1 1 4 2 4 1 4 1 2 4 1 4 5 1 5 5 2 1 5 2 b п 2
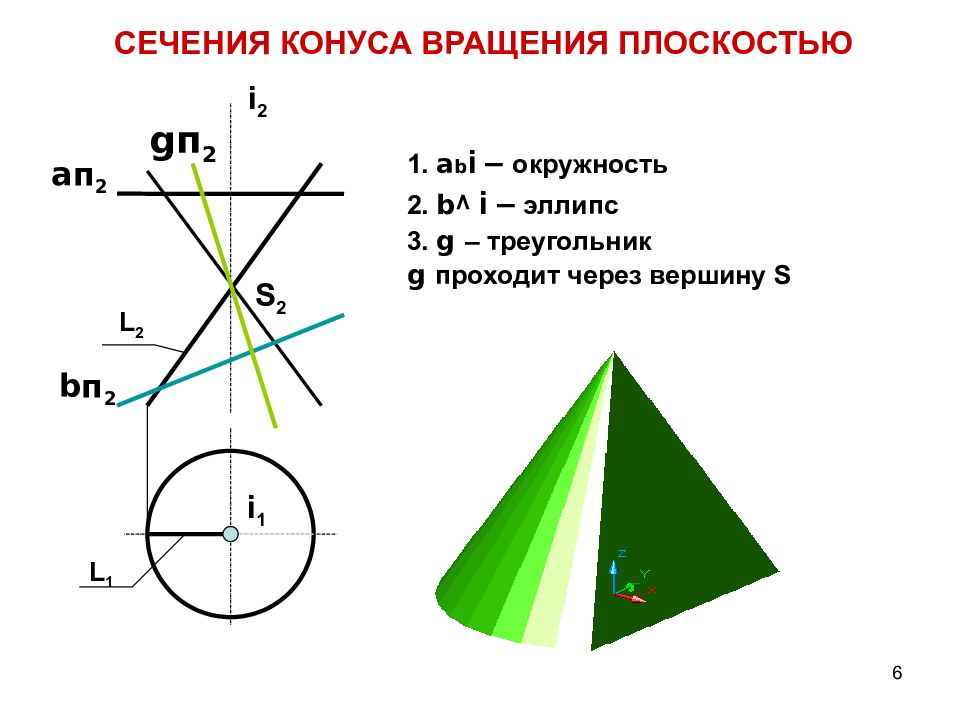
Слайд 6: СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
6 СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ 1. a b i – окружность 2. b ^ i – эллипс 3. g – треугольник g проходит через вершину S L 2 L 1 i 2 i 1 S 2 a п 2 b п 2 g п 2
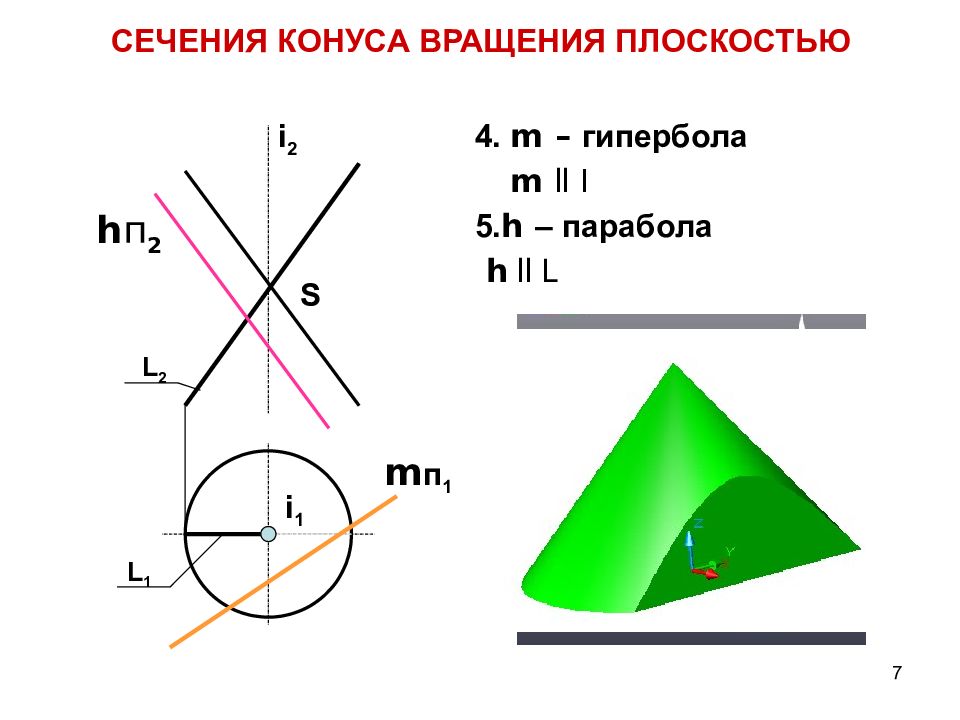
Слайд 7: СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
7 4. m – гипербола m ll I 5. h – парабола h ll L L 2 L 1 i 2 i 1 S СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ m п 1 h п 2
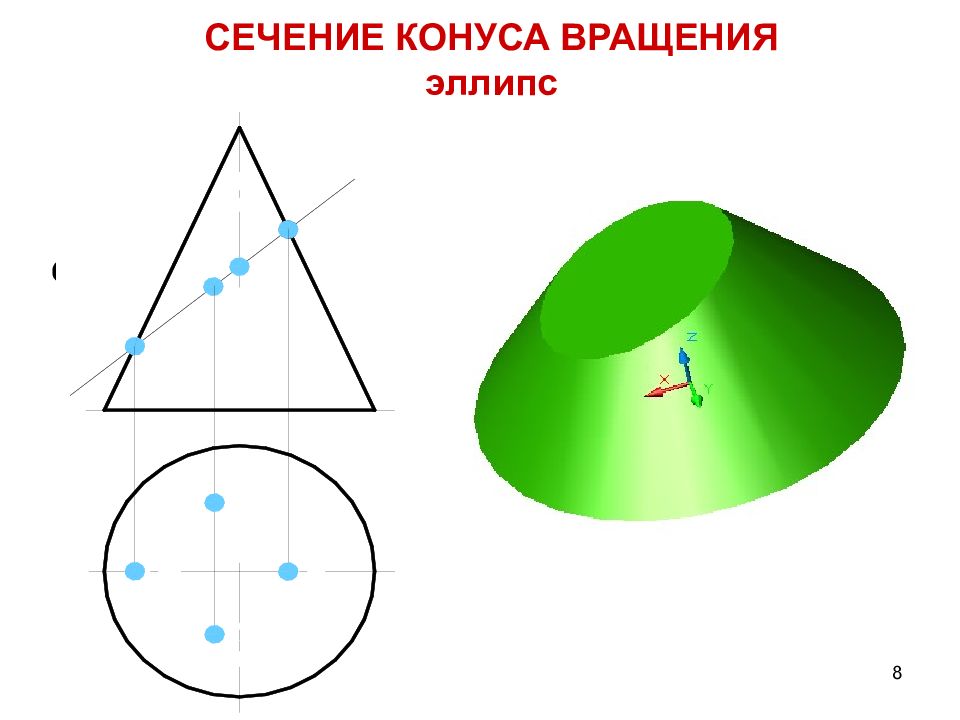
Слайд 8: СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ эллипс
8 СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ эллипс 2 2 1 2 3 2 1 1 2 1 α п2 R к 3 1 1 3 1 R к 4 1 4 1 1 4 2 1 2 3 1 1 3 1 2 1 1 2 2 2 3 2
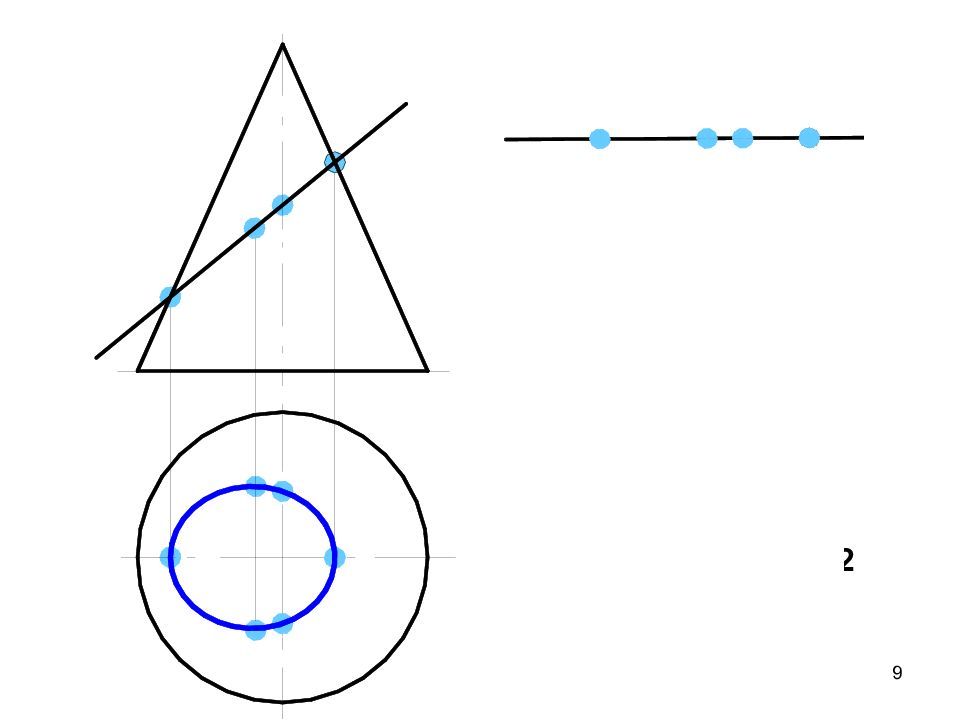
Слайд 9
9 1 2 1 1 4 2 3 2 2 2 2 1 4 1 4 1 1 3 1 1 3 1 1 2 1 3 2 1 4 2 1 2 2 1 1 2 3 1 3 4 1 4
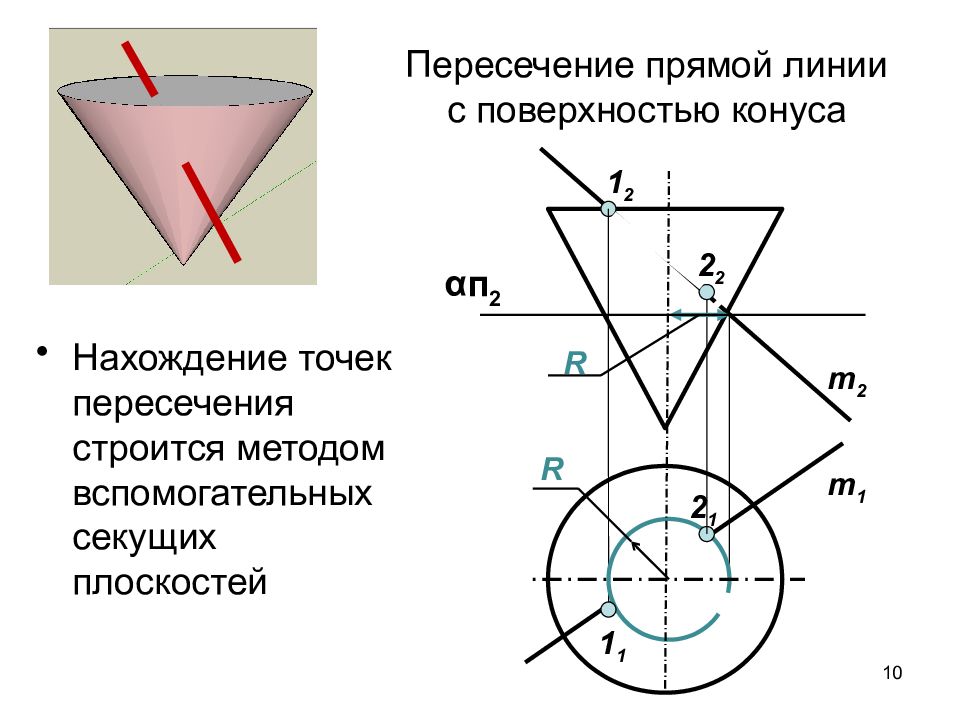
Слайд 10: Пересечение прямой линии с поверхностью конуса
Нахождение точек пересечения строится методом вспомогательных секущих плоскостей 10 m 2 m 1 1 2 1 1 2 2 2 1 R R α п 2
Слайд 11: СЕЧЕНИЯ СФЕРЫ
11 СЕЧЕНИЯ СФЕРЫ Сечение сферы плоскостью – окружность, которая может проецироваться как : - прямая линия - окружность - эллипс
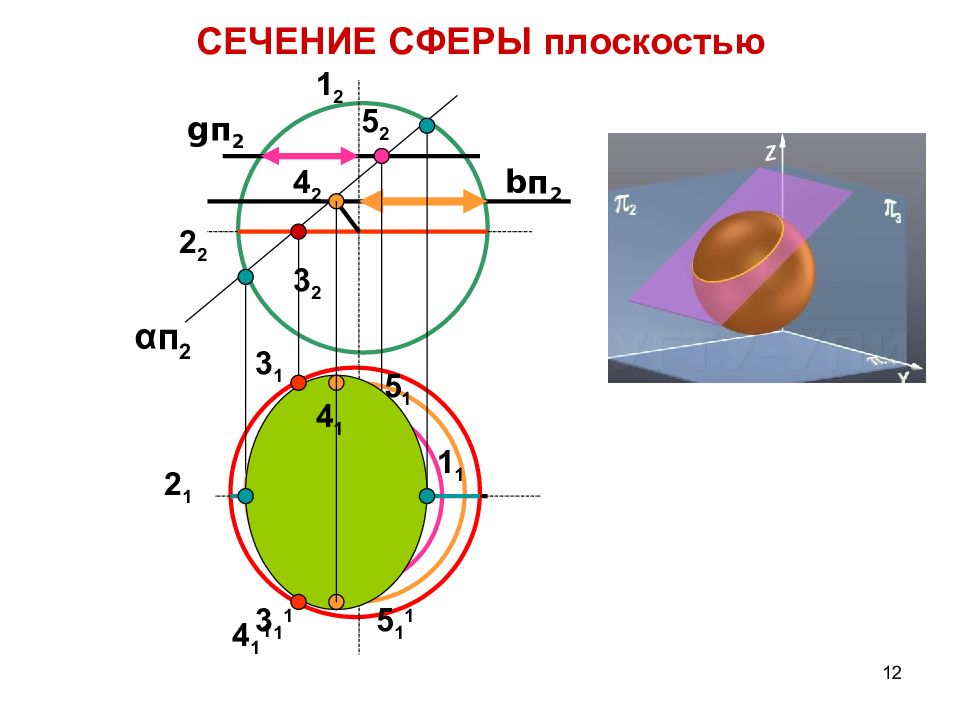
Слайд 12: СЕЧЕНИЕ СФЕРЫ плоскостью
12 СЕЧЕНИЕ СФЕРЫ плоскостью α п 2 1 2 1 1 2 2 2 1 3 2 3 1 3 1 1 4 2 b п 2 4 1 1 4 1 g п 2 5 2 5 1 5 1 1
Слайд 14
14 Линия пересечения поверхностей - совокупность точек одновременно принадлежащих двум пересекающимся поверхностям
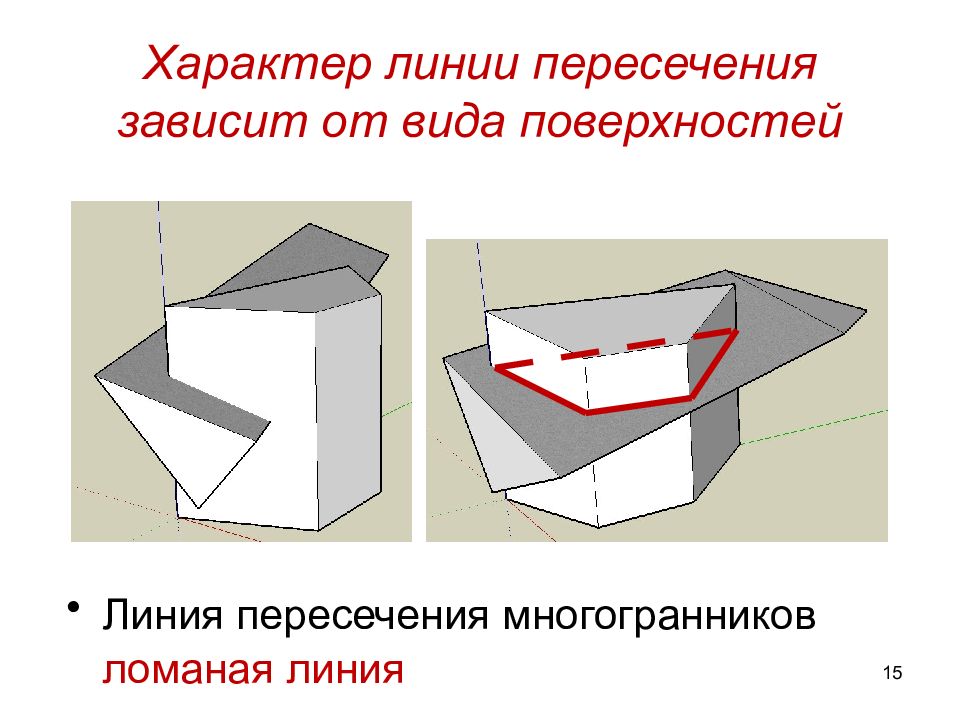
Слайд 15: Характер линии пересечения зависит от вида поверхностей
Линия пересечения многогранников ломаная линия 15
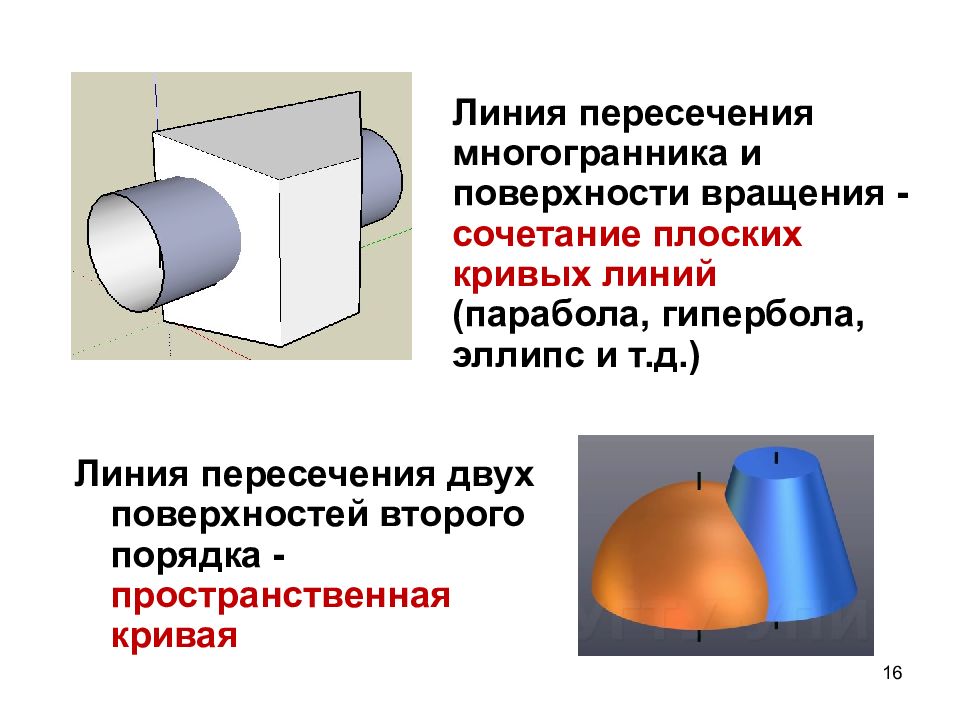
Слайд 16
16 Линия пересечения двух поверхностей второго порядка - пространственная кривая Линия пересечения многогранника и поверхности вращения - сочетание плоских кривых линий (парабола, гипербола, эллипс и т.д.)
Слайд 17
17 Алгоритм решения задач на построение линии пересечения поверхностей 1. Провести анализ заданных поверхностей - Определить характер заданных поверхностей (цилиндр, призма, сфера, пирамида и т.д.) Определить какая из них является проецирующей поверхностью На плоскости проекций, к которой поверхность перпендикулярна, проекция линии пересечения совпадает с очерком проецирующей поверхности
Слайд 18
18 2. Определить характерные (опорные) точки линии пересечения точки пересечения очерков поверхностей высшие и низшие, правые и левые точки поверхностей наиболее удаленные и приближенные к плоскостям проекций точки точки принадлежащие очерковым линиям поверхностей
Слайд 19
19 3. Провести вспомогательную секущую плоскость частного положения между опорными точками. В сечении поверхностей должны получаться простые геометрические фигуры – окружности, треугольники, прямоугольники. 4. Построить сечения заданных поверхностей вспомогательной секущей плоскостью. Определить точки пересечения построенных сечений. 5. Обозначить искомые точки линии пересечения поверхностей. Повторение пунктов 3,4,5 – n раз
Слайд 20
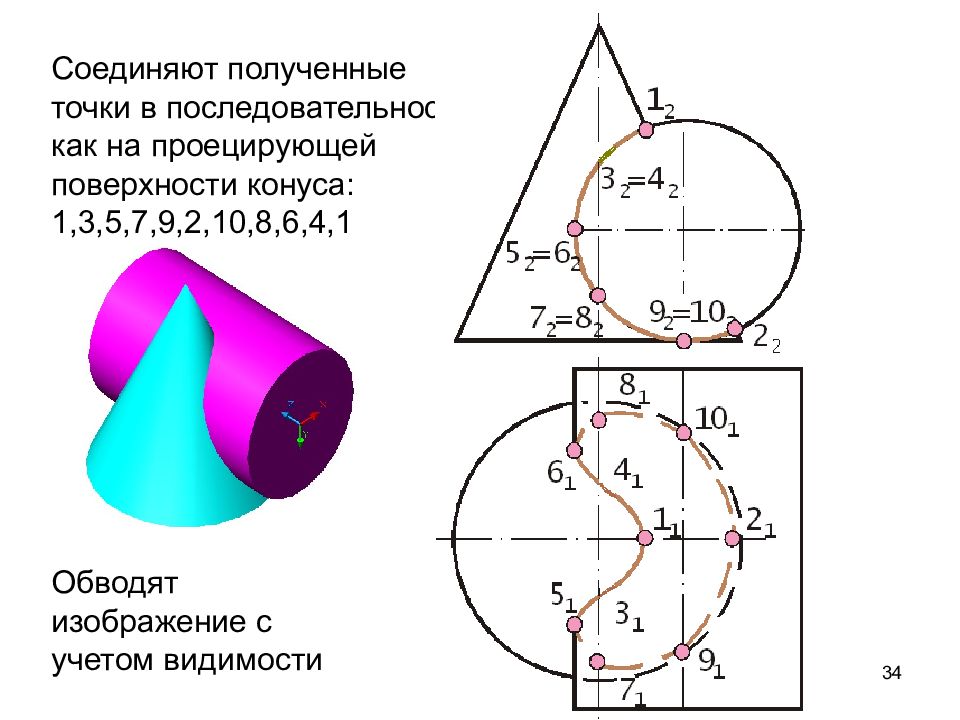
20 6. Соединить линией, полученные точки пересечения. Сохранить последовательность соединения точек, как на проецирующей поверхности 7. Определить видимость линии пересечения и очерковых линий заданных поверхностей 8. Обвести изображение данных поверхностей с учетом видимости изображения оставляя линии построения
Слайд 21
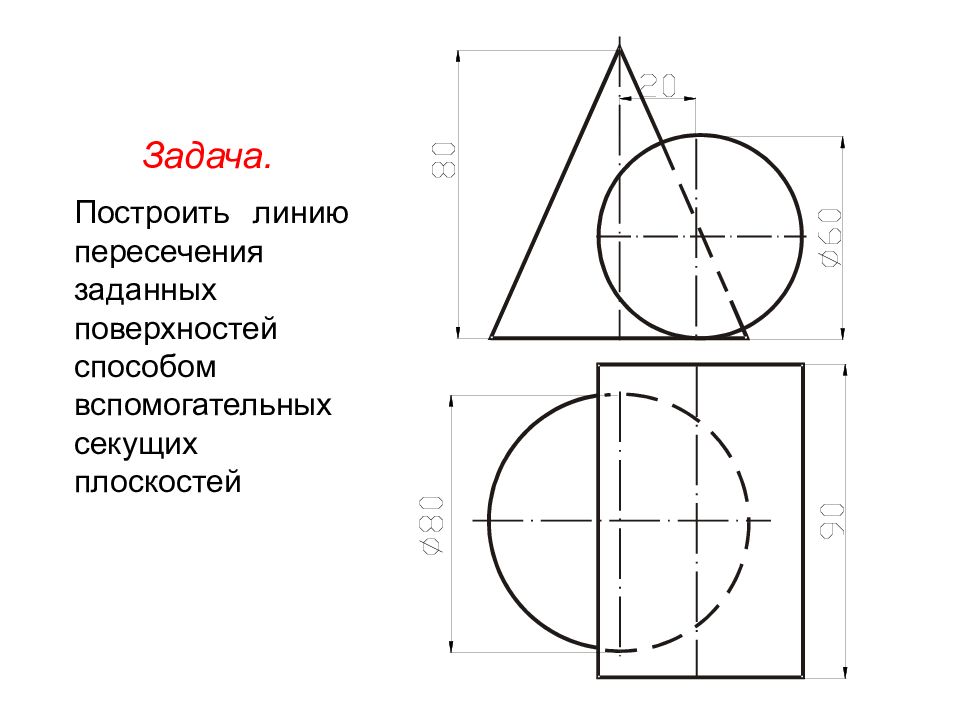
21 Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
Слайд 22
22 1. Провести анализ данных поверхностей Пересекаются призма и сфера. Поверхность призмы является проецирующей на горизонтальной плоскости, поэтому линия пересечения на эту плоскость проецируется в простую геометрическую фигуру - треугольник
Слайд 23
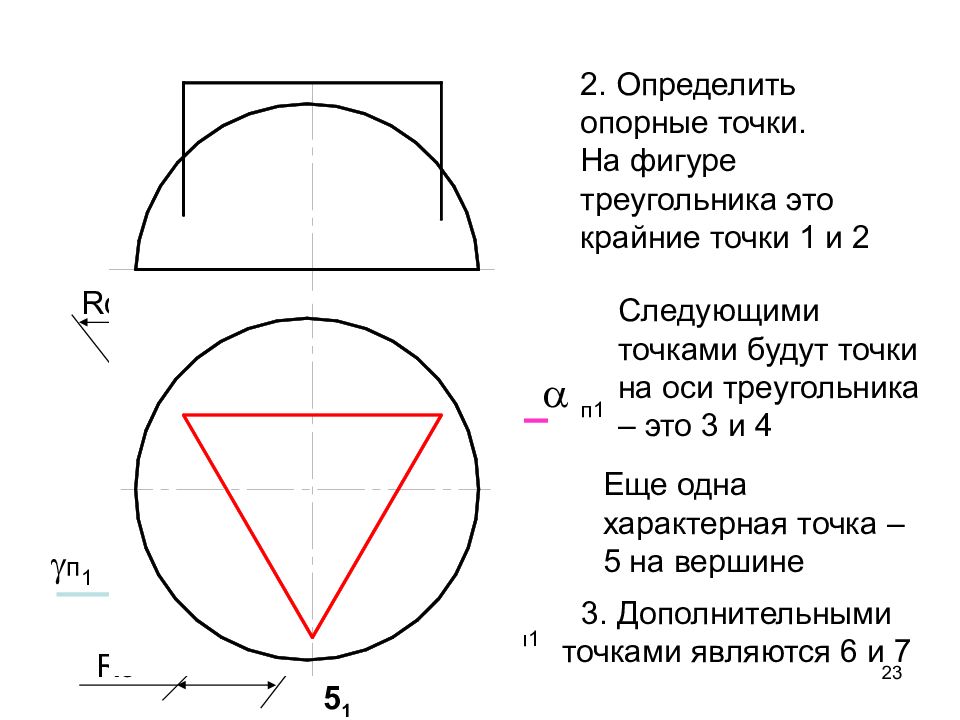
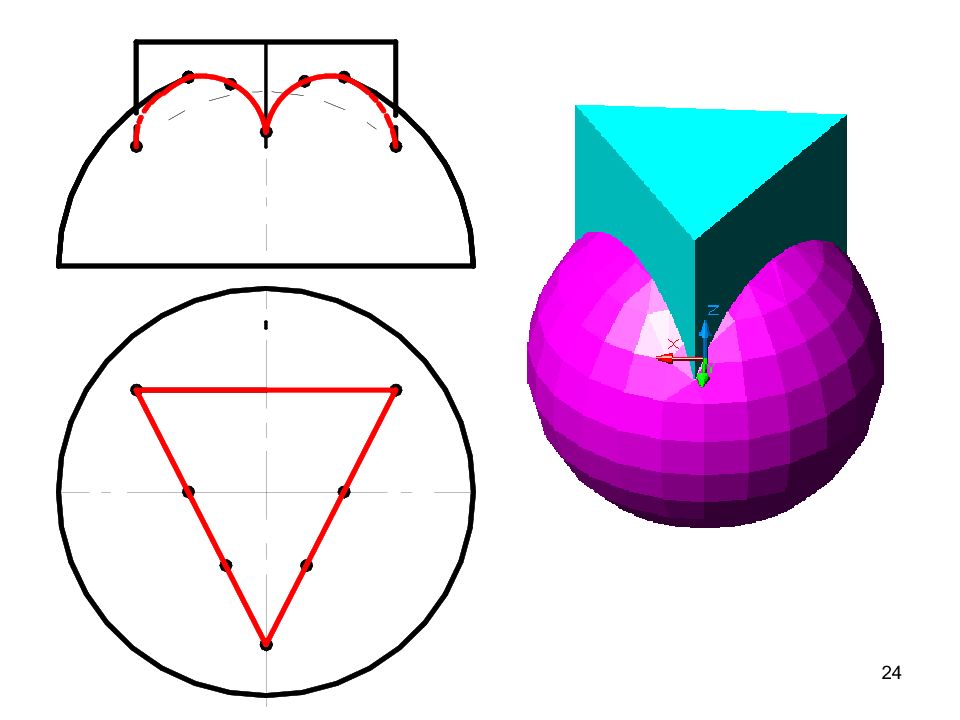
23 п1 Rc 1 1 2 2 1 2 2 1 4 2 3 2 4 1 3 1 b п1 Rc 5 1 5 2 п 1 6 1 7 1 6 2 7 2 0 1 0 2 2. Определить опорные точки. На фигуре треугольника это крайние точки 1 и 2 Следующими точками будут точки на оси треугольника – это 3 и 4 Еще одна характерная точка – 5 на вершине 3. Дополнительными точками являются 6 и 7
Слайд 25
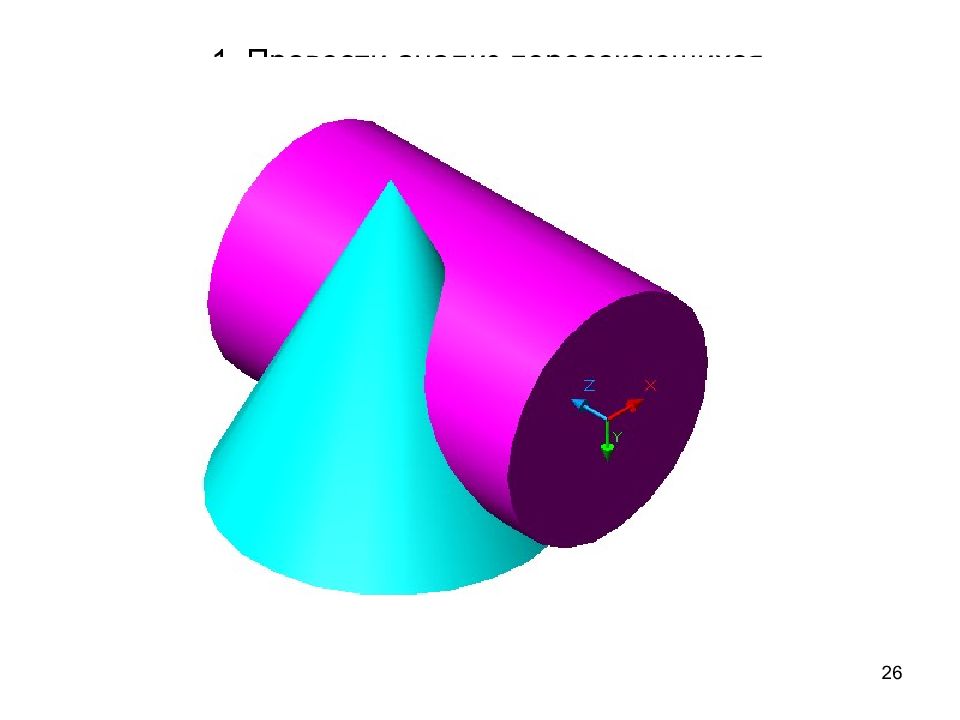
25 Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей 30
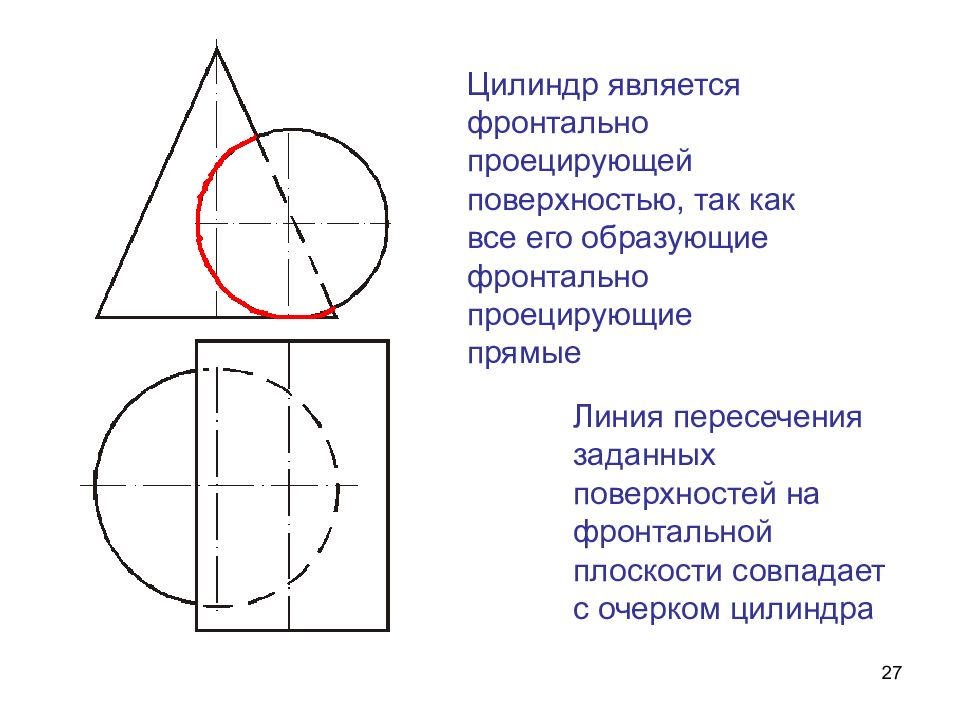
Слайд 27
27 Линия пересечения заданных поверхностей на фронтальной плоскости совпадает с очерком цилиндра Цилиндр является фронтально проецирующей поверхностью, так как все его образующие фронтально проецирующие прямые
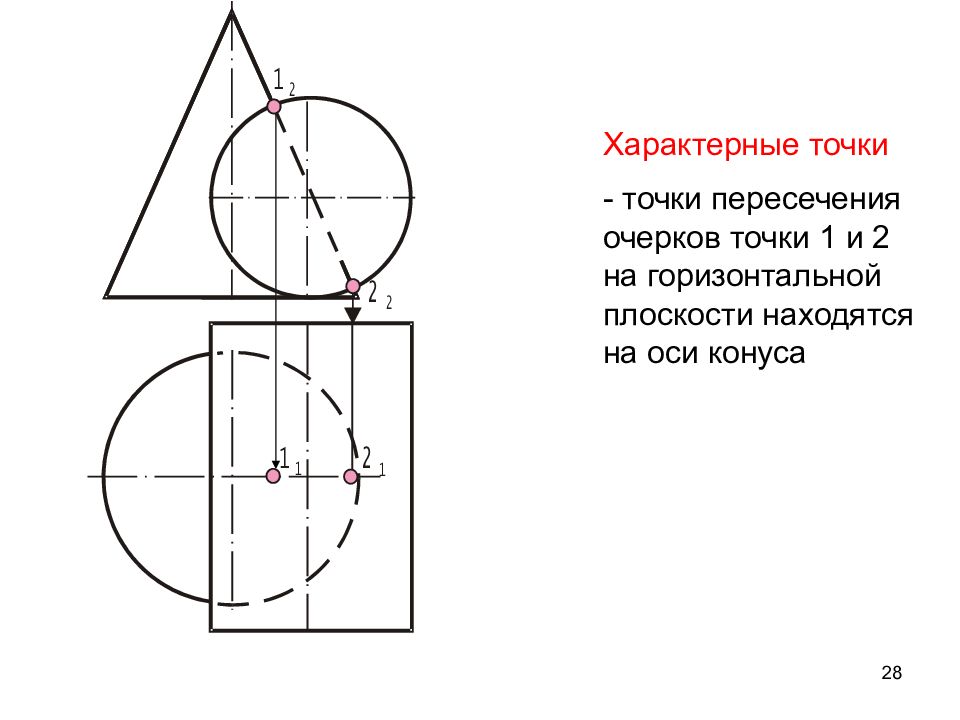
Слайд 28
28 Характерные точки - точки пересечения очерков точки 1 и 2 на горизонтальной плоскости находятся на оси конуса
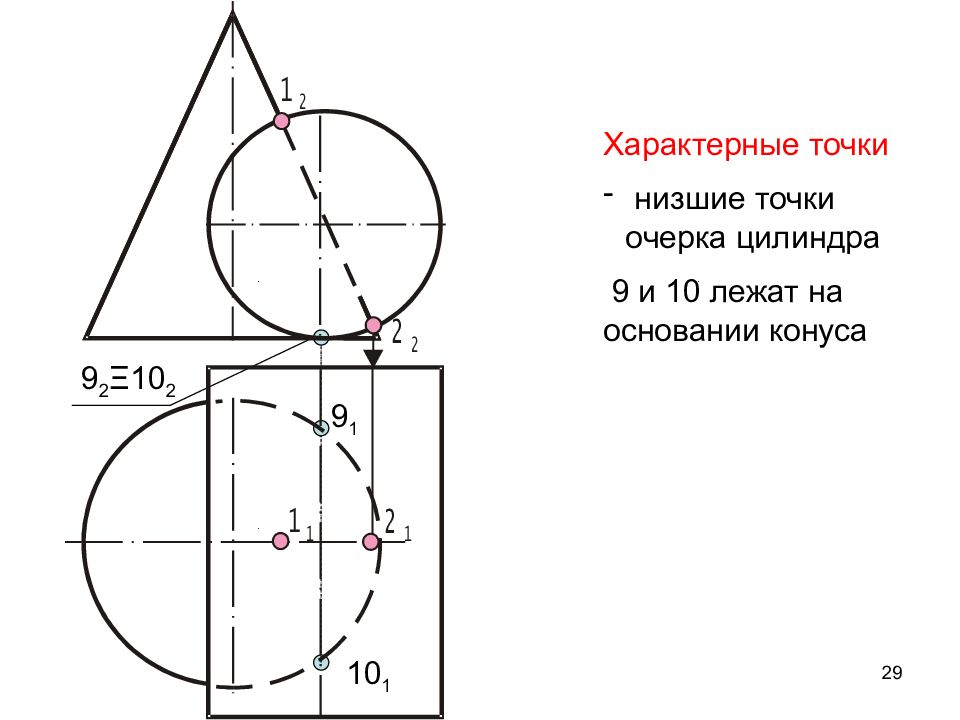
Слайд 29
29 Характерные точки низшие точки очерка цилиндра 9 и 10 лежат на основании конуса 9 2 Ξ 10 2 9 1 10 1
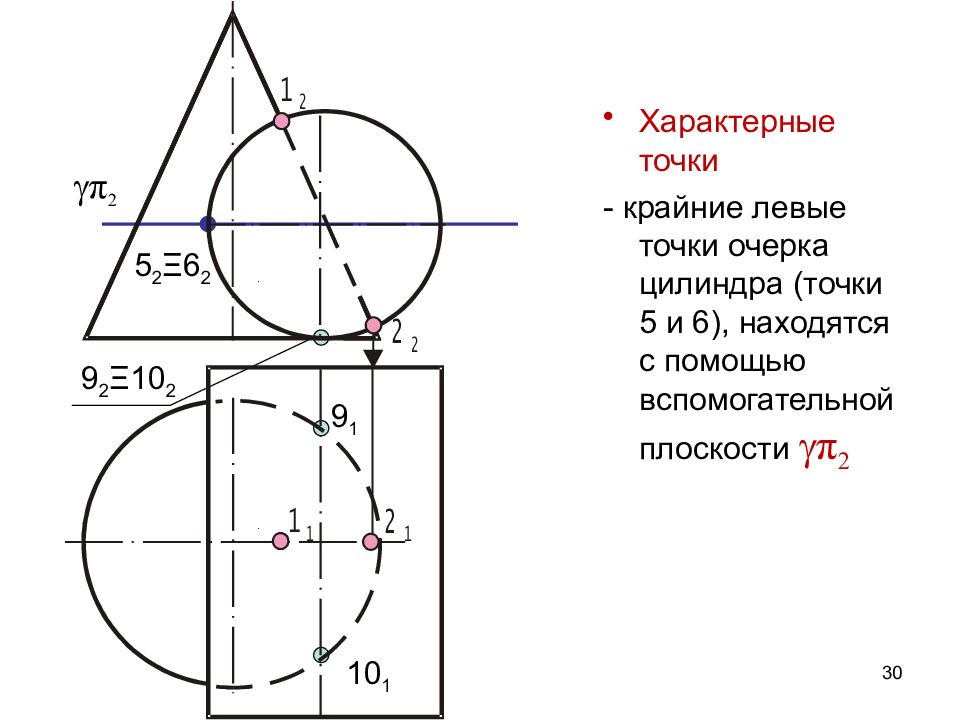
Слайд 30
30 Характерные точки - крайние левые точки очерка цилиндра (точки 5 и 6), находятся с помощью вспомогательной плоскости π 2 9 2 Ξ 10 2 9 1 10 1 π 2 5 2 Ξ 6 2
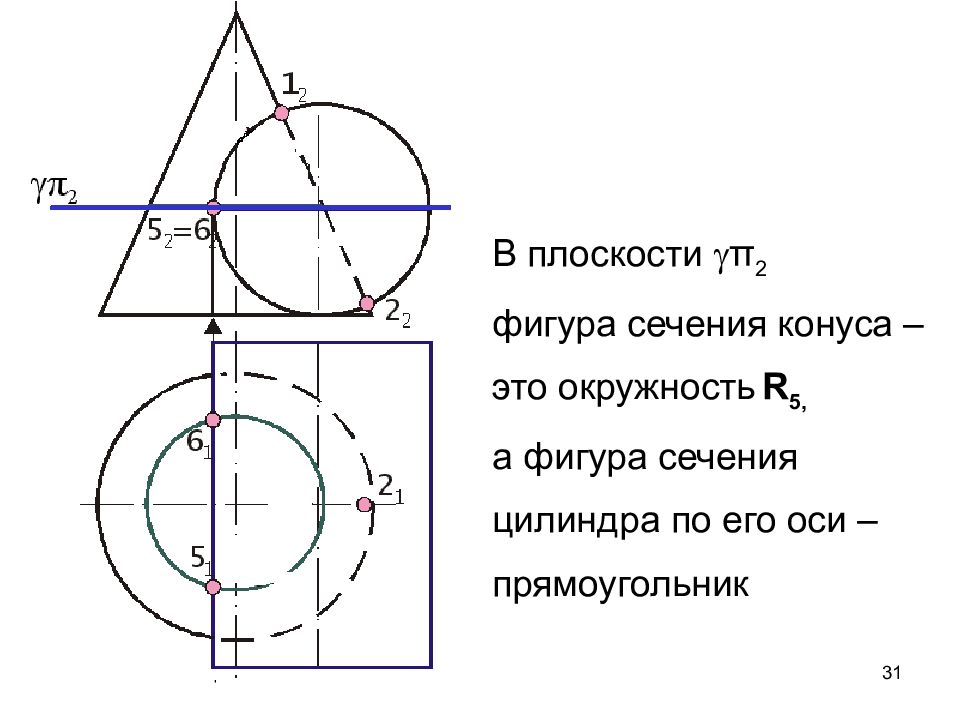
Слайд 31
31 R 5 В плоскости π 2 фигура сечения конуса – это окружность R 5, а фигура сечения цилиндра по его оси – прямоугольник
Слайд 32
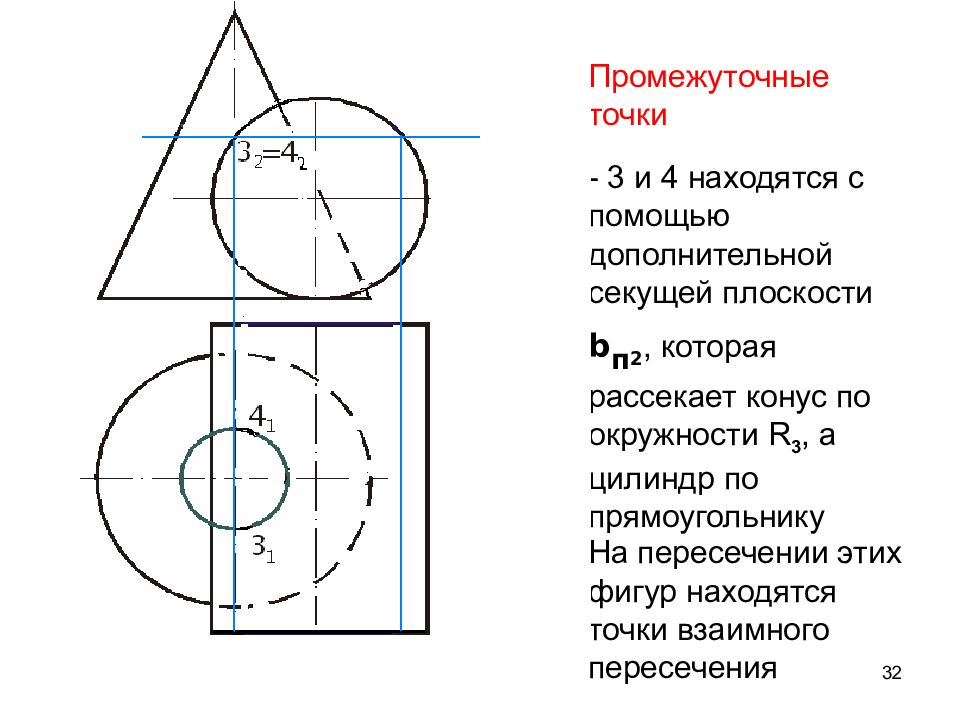
32 Промежуточные точки - 3 и 4 находятся с помощью дополнительной секущей плоскости b п 2, которая рассекает конус по окружности R 3, а цилиндр по прямоугольнику b п 2 R 3 На пересечении этих фигур находятся точки взаимного пересечения
Слайд 33
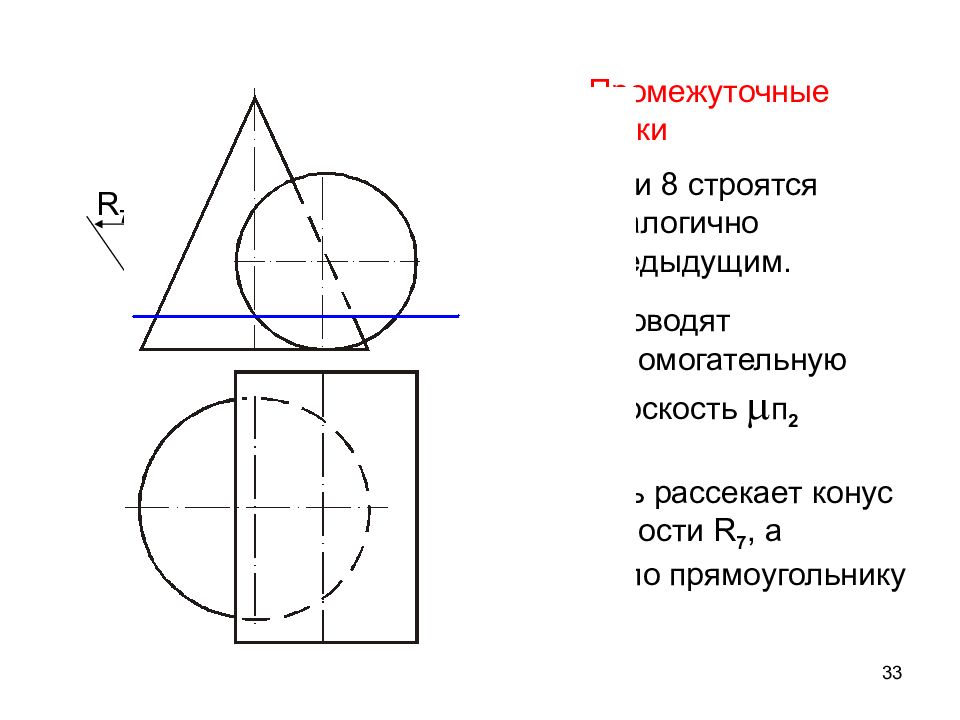
33 Промежуточные точки - 7 и 8 строятся аналогично предыдущим. Проводят вспомогательную плоскость п 2 R 7 8 1 7 1 7 2 Ξ 8 2 п 2 Плоскость рассекает конус по окружности R 7, а цилиндр по прямоугольнику